1 引言
流行性感冒是由流感病毒所致的感染, 主要通过日常的接触传染. 流感的传染能力强, 并且流感病毒变异速度快, 人群缺乏普适免疫力. 尤其是幼儿和老年人等免疫系统较弱的人群, 感染流感病毒后容易发展成为重症病例. 每年约有 250, 000-500, 000人死于流感. 人类在感染流感后一周, 体内会产生流感抗体, 并且该抗体在短期内不会消失. 在同一流感流行季, 具有流感抗体的人群对流感具有一定的免疫力, 不会再次感染同类型的流感病毒. 接种疫苗和流感治疗是抑制流感传染的两种有效方法. 甲型 H3N2 亚型及乙型 Yamagata 系疫苗可有效降低接种者罹患流感和严重并发症的风险. 奥司他韦、扎那米韦等神经氨酸酶抑制剂是甲型和乙型流感的有效治疗药物, 能显著降低流感重症和死亡的发生率. 罗道清[3 ] 发现接种流感疫苗能有效降低发生率及并发症.
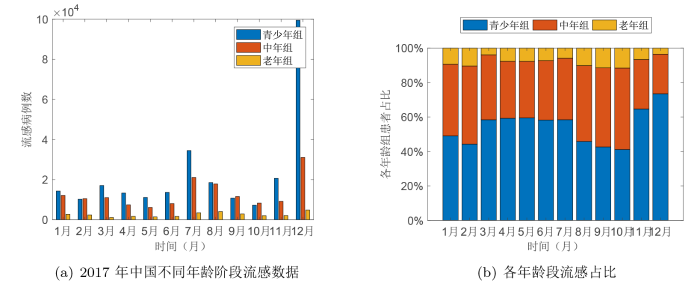
流感传播具有明显的年龄异质性. 图1(a) 给出 2017 年中国流感年龄分布数据[14 ] . 在三个年龄组中, 青少年流感患者普遍偏多, 老年患者最少且分布较平均; 图1(b) 直观地展现了各年龄组染病者占比. 发现大多数月份青少年患者占比超 50%, 少数月份青少年患者和中年患者占比相近, 老年患者占比约为 5%-10%. 因此, 辨识年龄异质性对流感传播的影响关键因素, 对于预防与控制流感传播至关重要.
图1
许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为.
但由于医疗资源的有限性及流感疫苗免疫能力的局限性, 利用有限资源使利益最大化是政府及决策者的理想选择. 以利益为出发点, 许多学者考虑最佳年龄接种分配方案、最小化感染病例或死亡病例等一系列最优控制策略[4 ,6 ] . 大多数模型都假设人群是均匀混合的和人的年龄无关, 不能精准捕捉流感传播的年龄异质性. 为此, 我们提出一类具有连续年龄结构的流感模型, 综合评估最优接种及治疗策略. 年龄结构传染病模型最优控制问题本质上属于$ L^1 $
2 模型
基于 Kermack-McKendirck 的仓室建模思想, 流感模型遵循 SIR 结构. 考虑年龄异质性对流感的影响, 我们将 $ t $ $ a $ $ p(a,t) $ $ s(t,a) $ $ i(t,a) $ $ r(t,a) $ $ t $ $ a $
$\hat\Lambda(a,t)=\bar\beta\int_0^{A}k(a,b)\frac{i(b,t)}{p(b,t)}{\rm d}b$
感染, 其中 $ k(a,b) $ $ b $ $ a $ $ \bar\beta $ $ A $
(2.1) $\begin{equation} \left\{ \begin{aligned} &\frac{{\partial s\left( {a,t} \right)}}{{\partial t}} + \frac{{\partial s\left( {a,t} \right)}}{{\partial a}} = - {\rm{\hat \Lambda }}\left( {a,t} \right)s\left( {a,t} \right) - \left( {\mu \left( a \right) + {u_1}\left( {a,t} \right)} \right)s\left( {a,t} \right),\\ &\frac{{\partial i\left( {a,t} \right)}}{{\partial t}} + \frac{{\partial i\left( {a,t} \right)}}{{\partial a}} = {\rm{\hat \Lambda }}\left( {a,t} \right)s\left( {a,t} \right) - \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right) + \mu \left( a \right)} \right)i\left( {a,t} \right),\\ &\frac{{\partial r\left( {a,t} \right)}}{{\partial t}} + \frac{{\partial r\left( {a,t} \right)}}{{\partial a}} = {u_1}\left( {a,t} \right)s\left( {a,t} \right) + \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right)} \right)i\left( {a,t} \right) - \mu \left( a \right)r(a,t),\\ &s\left( {0,t} \right) = \mathop \smallint \nolimits_0^A \beta \left( a \right)p\left( {a,t} \right){\rm d}a,\quad i(0,t)=r(0,t) = 0, \end{aligned} \right. \end{equation}$
$ \gamma(a) $ $ \beta(a) $ $ a $ $ \mu(a) $ $ a $ $ u_j(a,t)\ (j=1,2) $ $ t $ $ a $
(1) $ \beta(\cdot),\gamma(\cdot)\in L^\infty; $
(2) 对于任意 $ a\in\mathbb R_+, $ $ k_1(a)\le k(a,\cdot)\le k_2(a), $ $ k_1(\cdot),k_2(\cdot)\in L^\infty\cap L^1; $
(3) 存在区间 $ [a_1,a_2]\subset[A] $ $ \int_{a_1}^{a_2}k_1(a){\rm d}a>0; $
(4) $ \mu(\cdot)\in L^1_{Loc}(\mathbb R_+) $ $ \int_0^A\mu(a){\rm d}a\rightarrow+\infty. $
(2.2) $\begin{matrix}& \frac{\partial p(a,t)}{\partial a}+\frac{\partial p(a,t)}{\partial t}=-\mu(a)p(a,t),\notag \\ & p(t,0)=\int_0^A\beta(a)p(a,t){\rm d}a, \\ &p(0,a)=p_0(a)\in L^1(0,A).\notag \end{matrix}$
方程(2.2)是一个经典的 Mckendrick-Von Foester 方程. 由文献[1 ]知, 存在一个稳态分布
$p_\infty(a)=\frac{\int_0^Ap_\infty(a){\rm d}a}{\int_0^A{\rm e}^{-\int_0^a\mu(\tau){\rm d}\tau}{\rm d}a}{\rm e}^{-\int_0^a\mu(\tau){\rm d}\tau},$
当 $ t\rightarrow+\infty $ $ p(a,t)\rightarrow p_\infty(a) $ $ (a,t)\in(0,A)\times\mathbb R_+ $ $ p(a,t)=p_\infty(a). $
(2.3) $\begin{matrix} {\cal J}\left( {{u_1},{u_2}} \right) =& \int_0^T {\int_0^A \left[{A_0}i\left( {a,t} \right) + {A_1}{u_1}\left( {a,t} \right)s\left( {a,t} \right) + {A_2}{u_2}\left( {a,t} \right)i\left( {a,t} \right)\right]{\rm d}a{\rm d}t }\notag \\ &+ \frac{1}{2}\int_0^T \;\int_0^A \left({B_1}u_1^2\left( {a,t} \right) + {B_2}u_2^2\left( {a,t} \right)\right){\rm d}a{\rm d}t, \end{matrix}$
其中 $ T $ $ A_0,A_1,A_2 $ $ B_1 $ $ B_2 $ $ A_i>0,$ $i=0,1,2,B_j>0,j=1,2. $ $ (u_1,u_2)\in\mathcal U, $
$\mathcal U=\left\{({u_1},{u_2}) \in({L^\infty }((0,A) \times (0,T)),{L^\infty }((0,A) \times (0,T))|0 \le {u_1} \le {U_1},0 \le {u_2} \le {U_2}\right\}$
${\cal J}(u_1^*,u_2^*) = \min\limits_{ {u_1},{u_2} \in {\cal U}}{\cal J}\left( {{u_1},{u_2}} \right),$
对于任意 $ (u_1,u_2)\in\mathcal U, $ $ x^u $ $ \lambda^u. $ $ \mathcal L=(0,A)\times(0,T), $ $ \mathcal F[u]=(\mathcal F_1u_1,\mathcal F_2u_2), $
$\mathcal F_j[u_j]=\left\{ \begin{aligned} &0, u_j<0, \\ &u_j, 0\le u_j\le U_j, \\ &U_j, u_j>U_j. \end{aligned} \right.j=1,2,$
当 $ \phi=(\phi_1,\phi_2,\phi_3)\in \mathcal L^3, $
$\begin{aligned}& \|\phi\|_{L^1(\mathcal L)}=\sum\limits_{k=1}^3\int_0^T\int_0^A|\phi_k(a,t)|{\rm d}a{\rm d}t, \\ & \|\phi\|_{L^\infty(\mathcal L)}=\sum\limits_{k=1}^3\sup\limits_{(a,t)\in\mathcal L}|\phi_k(a,t)|.\end{aligned}$
从而, 在空间 $ L^1(\mathcal L) $
$\mathscr J[u]=\left\{ \begin{aligned} &\mathcal J(u), u\in\mathcal U, \\ &+\infty, u\notin\mathcal U. \end{aligned} \right.$
为了方便, 记控制变量为 $ u=(u_1,u_2) $ .
引理 2.1 当 $ T $
(1) 当 $ u,v\in\mathcal U, $ $ L^1 $ $ L^\infty $
$\begin{aligned}& \|x^u-x^v\|_{L^1}\le C_x^1\|u-v\|_{L^1}, \\ & \|x^u-x^v\|_{L^\infty}\le C_x^\infty\|u-v\|_{L^\infty};\end{aligned}$
(2) 泛函 $ \mathscr J $ $ L^1(\mathcal L) $
证 由于参数满足假设 2.1, 利用 $ L^1(\mathcal L) $
假设在空间 $ L^1(\mathcal L) $ $ u_n=(u_{1n},u_{2n})\rightarrow u=(u_1,u_2) $ $ u_n^2\rightarrow u^2. $
$\lim\limits_{n\rightarrow\infty}\|u_n^2\|_{L^1(\mathcal L)}=\|u^2\|_{L^1(\mathcal L)}.$
$\begin{aligned}&\|A_0(i^{u_n}-i^u)+A_1U_1(s^{u_n}-s^{u})+A_2U_2(i^{u_n}-i^u)\|_{L^1(\mathcal L)}\\ \le\ & \max\{A_0,A_1U_1,A_2U_2\}\|x^{u_n}-x^u\|_{L^1(\mathcal L)} \le C_f^1\|u_n-u\|_{L^1(\mathcal L)},\end{aligned}$
其中 $ C_1^f=\max\{A_0,A_1U_1,A_2U_2\}C_x^1. $
$\|\mathscr J[u_n]-\mathscr J[u]\|_{L^1(\mathcal L)}\le C_f^1\|u_n-u\|_{L^1(\mathcal L)}.$
定理 2.1 控制问题(2.1)-(2.3)存在最优解 $ (u_1^*,u_2^*)\in \mathcal U $
${\cal J}(u_1^*,u_2^*)=\min\limits_{(u_1,u_2)\in \mathcal U}{\cal J}(u_1,u_2).$
证 由引理2.1知, 状态方程(2.1)的解及控制变量 $ u_j\ (j=1,2) $ $ \inf\limits_{u\in\mathcal U}{\cal J}(u_1,u_2)>-\infty, $ $ u^n\in\mathcal U $ $ \lim\limits_{n\rightarrow+\infty}{\cal J}(u_1^n,u_2^n) $
$(s^n,i^n,r^n)=(s,i,r)(u_1^n,u_2^n).$
由状态变量对控制变量的连续依赖性知, 当 $ n\rightarrow+\infty $
$(s^n,i^n,r^n)=(s,i,r)(u_1^n,u_2^n)\rightarrow (s^*,i^*,r^*)(u_1^*,u_2^*).$
$\begin{align*} &\int_0^T \int_0^A \left({B_1}u_1^2\left( {a,t} \right) + {B_2}u_2^2\left( {a,t} \right)\right){\rm d}a{\rm d}t\\ \le\ &\liminf\limits_{n\rightarrow+\infty}\int_0^T \int_0^A \left({B_1}(u_1^n)^2\left( {a,t} \right) + {B_2}(u_2^n)^2\left( {a,t} \right)\right){\rm d}a{\rm d}t. \end{align*}$
$\begin{aligned} {\cal J}(u_1^*,u_2^*)=\,&\int_0^A\int_0^T\left[A_0i^*(a,t) + A_1u_1^*(a,t)s^*(a,t) + A_2u_2^*(a,t)i^*(a,t)\right. \\ &\left.+\frac{1}{2}\left(B_1(u_1^*)^2(a,t) + B_2(u_2^*)^2(a,t)\right)\right]{\rm d}a{\rm d}t \\ \le\,&\liminf\limits_{n\rightarrow+\infty}\int_0^A\int_0^T\left[A_0i^n(a,t) + A_1u_1^n(a,t)s^n(a,t) + A_2u_2^n(a,t)i^n(a,t)\right. \\ &\left.+\frac{1}{2}\left(B_1(u_1^n)^2(a,t) + B_2(u_2^n)^2(a,t)\right)\right]{\rm d}a{\rm d}t=\inf\limits_{u\in\mathcal U}{\cal J}(u_1,u_2). \end{aligned}$
故 $ (u_1^*,u_2^*) $ $ {\cal J}(u_1,u_2) $ .
接下来, 我们将利用庞特里亚金最大值原理得到最优控制对. 引入拉格朗日乘子$ \lambda = (q,\xi, \eta ) $ $ {\cal H} $
$\begin{aligned} &{\cal H}(x,u,\lambda)\\ =\ & {\cal J}({u_1},{u_2})- \int_ 0^T\int_0^ Aq(a,t)[{s_t} + {s_a} + {\rm{\hat \Lambda }}\left( {a,t} \right)s(a,t) + \left( {\mu \left( a \right) + {u_1}\left( {a,t} \right)} \right)s\left( {a,t} \right)]{\rm d}a{\rm d}t \\ & - \int_0^T {\int _0^ A\xi (a,t)[{i_t} + {i_a} - {\rm{\hat \Lambda }}\left( {a,t} \right)s(a,t) + \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right) + \mu \left( a \right)} \right)i\left( {a,t} \right)]} {\rm d}a{\rm d}t\\ & - \int_0^T {\int _0^ A\eta (a,t)[{r_t} + {r_a} - {u_1}(a,t)s(a,t) - \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right)} \right)i\left( {a,t} \right) + \mu \left( a \right)r \left( a,t \right)]} {\rm d}a{\rm d}t\\ & - \int_0^T \;q(0,t)[s(0,t) - \mathop \int \nolimits_0^A \beta \left( a \right)p\left( {a,t} \right){\rm d}a]{\rm d}t \\ =:& \int_0^T\int_0^AH(a,t){\rm d}a{\rm d}t- \int \nolimits_0^T \;q(0,t)s(0,t){\rm d}t, \end{aligned}$
$\begin{aligned} H(a,t)=\ &{A_0}i\left( {a,t} \right) + {A_1}{u_1}\left( {a,t} \right)s\left( {a,t} \right) + {A_2}{u_2}\left( {a,t} \right)i\left( {a,t} \right){\rm d}a{\rm d}t \\ & +\frac{1}{2}\left({B_1}u_1^2\left( {a,t} \right) + {B_2}u_2^2\left( {a,t} \right)\right)-q(0,t)\beta \left( a \right)p\left( {a,t} \right) \\ & -q(a,t)[{s_t} + {s_a} + {\rm{\hat \Lambda }}\left( {a,t} \right)s(a,t) + \left( {\mu \left( a \right) + {u_1}\left( {a,t} \right)} \right)s\left( {a,t} \right)] \\ & -\xi (a,t)[{i_t} + {i_a} - {\rm{\hat \Lambda }}\left( {a,t} \right)s(a,t) + \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right) + \mu \left( a \right)} \right)i\left( {a,t} \right)] \\ & -\eta (a,t)[{r_t} + {r_a} - {u_1}(a,t)s(a,t) - \left( {\gamma \left( a \right) + {u_2}\left( {a,t} \right)} \right)i\left( {a,t} \right) + \mu \left( a \right)r \left( a,t \right)]. \end{aligned}$
定理 2.2 对于任意 $ u\in\mathcal U, $
(2.4) $\begin{equation} \left\{ \begin{aligned} &{q_a} + {q_t} = - \beta (a)q(0,t) + (q(a,t) - \xi (a,t)){\rm{\hat \Lambda }}\left( {a,t} \right) - {A_1}{u_1}(a,t)\\ & + (\mu (a) + {u_1}(a,t))q(a,t) - \eta (a,t){u_1}(a,t),\\ &{\xi _a} + {\xi _t} = - \beta (a)q(0,t) + (\mu (a) + \gamma (a) + {u_2}(a,t))\xi (a,t)\\ & - (\gamma (a) + {u_2}(a,t))\eta (a,t) - {A_0} - {A_2}{u_2}(a,t)\\ & - \frac{1}{{p_\infty(a)}}\int_0^A {(q(x,t) - \xi (x,t))k(x,a)s(x,t){\rm d}x}, \\ &{\eta _a} + {\eta _t} = - \beta (a)q(0,t) + \mu (a)\eta (a,t) \end{aligned} \right. \end{equation}$
$\begin{aligned} &q(A,t) = \xi (A,t) = \eta (A,t) = 0,\\ & q(a,T) = \xi (a,T) = \eta (a,T) = 0. \end{aligned}$
另外, 伴随系统(2.4)存在一个利普希茨连续的弱解, 即对于任意 $ u,v\in\mathcal U, $
$\|\lambda^u-\lambda^v\|_{L^\infty}\le C_\lambda^\infty\|u-v\|_{L^\infty}.$
$\frac{\partial \lambda(a,t)}{\partial a}+\frac{\partial \lambda(a,t)}{\partial t}=-\frac{\partial H(a,t)}{\partial x}.$
直接求导可得伴随系统(2.1). 结合引理2.1及假设2.1, 伴随系统(2.4)解的利普希茨连续性成立.
定理 2.3 若 $ (u_1^*,u_2^*) $ $ \mathscr J $
$u_1^*(a,t) = \min \left\{ {\max(0,{{\bar u}_1}),{U_1}} \right\},\ u_2^*(a,t) = \min \left\{ {\max (0,{{\overline u }_2}),{U_2}} \right\},$
${\bar u_1}(a,t) = \frac{{s(a,t)(q(a,t) - \eta (a,t) - {A_1})}}{{{B_1}}},\ {\bar u_2}(a,t) = \frac{{i(a,t)(\xi (a,t) - \eta (a,t) - {A_2})}}{{{B_2}}}.$
证 直接利用 $ \frac{\partial{\cal H}(a,t)}{\partial u_j}=0,j=1,2 $
$\begin{aligned} {\bar u_1}(a,t) = \frac{{s(a,t)(q(a,t) - \eta (a,t) - {A_1})}}{{{B_1}}}, \ {\bar u_2}(a,t) = \frac{{i(a,t)(\xi (a,t) - \eta (a,t) - {A_2})}}{{{B_2}}}. \end{aligned}$
因此, 对于任意 $ u\in\mathcal U, $
$u_1^*(a,t) = \min \left\{ {\max(0,{{\bar u}_1}),{U_1}} \right\},\ u_2^*(a,t) = \min \left\{ {\max (0,{{\overline u }_2}),{U_2}} \right\}.$
虽然我们得到泛函 $ \mathscr J $ $ L^1 $ $ L^1 $ $ \epsilon>0, $ $ u_\epsilon\in L^1(\mathcal L) $
(2.5) $\mathscr J(u_\epsilon)\le \inf\limits_{u\in\mathcal U}\mathscr J(u)+\epsilon,$
(2.6) $\mathscr J(u_\epsilon)\le \inf\limits_{u\in\mathcal U}\mathscr J(u)+\sqrt{\epsilon}\|u_\epsilon-u\|_{L^1}.$
$\mathscr J_\epsilon(u)=\mathscr J(u)+\sqrt{\epsilon}\|u_\epsilon-u\|_{L^1}.$
引理 2.2 若 $ u_\epsilon $ $ \mathscr J_\epsilon(u), $
$u_\epsilon=\mathcal F\left(\tilde u_1(x^{u_\epsilon},\lambda^{u_\epsilon})+\sqrt{\epsilon}\pi_1^\epsilon,\tilde u_2(x^{u_\epsilon},\lambda^{u_\epsilon})+\sqrt{\epsilon}\pi_2^\epsilon\right).$
其中 $ \pi_j^\epsilon\in L^\infty(\mathcal L) $ $ |\pi_j^\epsilon|\le1\ (j=1,2) $
$\begin{aligned} \tilde u_1(x^{u_\epsilon},\lambda^{u_\epsilon})=\frac{{s^{u_\epsilon}(a,t)(q^{u_\epsilon}(a,t) - \eta^{u_\epsilon} (a,t) - {A_1})}}{{{B_1}}}, \\ \tilde u_2(x^{u_\epsilon},\lambda^{u_\epsilon})=\frac{{i^{u_\epsilon}(a,t)(\xi^{u_\epsilon} (a,t) - \eta^{u_\epsilon} (a,t) - {A_2})}}{{{B_2}}}. \end{aligned}$
定理 2.4 若 $ T $ $ u^*\in\mathcal U $ $ \mathscr J(u) $
证 对于任意 $ u,v\in\mathcal U, $ $ C_1 $
$\begin{aligned} &\quad\ \|\mathcal F_1[u_1]-\mathcal F_1[v_1]\|_{L^\infty} \\ &=\left\| \frac{s^{u_1}(a,t)(q^{u_1}(a,t) - \eta^{u_1} (a,t) - {A_1})}{B_1}-\frac{s^{v_1}(a,t)(q^{v_1}(a,t) - \eta^{v_1} (a,t) - {A_1})}{B_1}\right\|_{L^\infty} \\ &\le\frac{TC_1}{B_1}\|u-v\|_{L^\infty}. \end{aligned}$
$\|\mathcal F_2[u_2]-\mathcal F_2[v_2]\|_{L^\infty}\le\frac{TC_2}{B_2}\|u-v\|_{L^\infty}.$
为了方便, 定义函数 $ \mathscr G:\mathcal U\rightarrow\mathcal U $
$\mathscr G[u]=\mathcal F(\tilde u_1(x^u,\lambda^u),\tilde u_2(x^u,\lambda^u)).$
再由状态变量及伴随变量的利普希茨连续性知, 存在正常数 $ C_3 $
$\|\mathscr G[u]-\mathscr G[v]\|_{L^\infty}\le TC_3\left(\frac{1}{B_1}+\frac{1}{B_2}\right)\|u-v\|_{L^\infty}.$
故当 $ TC_3\left(\frac{1}{B_1}+\frac{1}{B_2}\right)<1, $ $ \mathscr G $ $ u^* $ . 注意到对于任意 $ u_\epsilon\in\mathcal U $
$\|\mathscr G[u_\epsilon]-u_\epsilon\|_{L^\infty}\le\sqrt{\epsilon}\left(\frac{1}{B_1}+\frac{1}{B_2}\right).$
接下来证明在 $ L^\infty $ $ \epsilon\rightarrow0 $ $ u_\epsilon\rightarrow u^* $ . 事实上, 当 $ u_\epsilon\in\mathcal U, $
$\begin{align*} \|u^*-u_\epsilon\|_{L^\infty}&=\|\mathscr G[u^*]-u_\epsilon\|_{L^\infty} \le\|\mathscr G[u^*]-\mathscr G[u_\epsilon]\|_{L^\infty}+\|\mathscr G[u_\epsilon]-u_\epsilon\|_{L^\infty} \\ &\le TC_3\left(\frac{1}{B_1}+\frac{1}{B_2}\right)\|u^*-u_\epsilon\|_{L^\infty}+\sqrt{\epsilon}\left(\frac{1}{B_1}+\frac{1}{B_2}\right). \end{align*}$
因此, 若存在常数 $ C_3T\left(\frac{1}{B_1}+\frac{1}{B_2}\right) $
$\|u^*-u_\epsilon\|_{L^\infty}\le\frac{\sqrt{\epsilon}\left(\frac{1}{B_1}+\frac{1}{B_2}\right)}{1-C_3T\left(\frac{1}{B_1}+\frac{1}{B_2}\right)}.$
故在 $ L^\infty $ $ \epsilon\rightarrow0 $ $ u_\epsilon\rightarrow u^* $ .
利用 Ekland 变分原理知, 当 $ \epsilon\rightarrow0, $ $ \mathscr J(u^*)\le\inf\limits_{u\in\mathcal U}\mathscr J(u). $
定理2.1-定理2.4表明当 $ T $ $ (u_1,u_2) $
${\cal J}(u_1^*,u_2^*) = \min\limits_{ {u_1},{u_2} \in {\cal U}}{\cal J}\left( {{u_1},{u_2}} \right).$
3 数值模拟
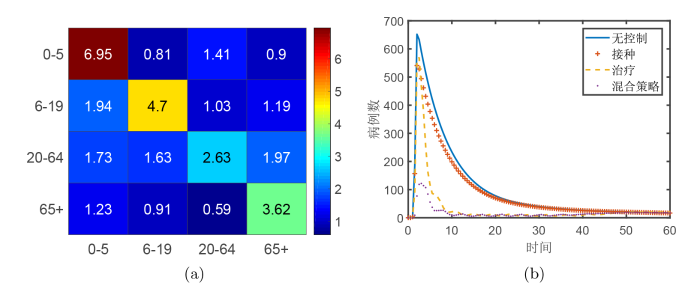
本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
图2
图2
(a) 接触矩阵; (b) 四种不同策略下流感患者时间序列图
另外, 据调查研究[13 ] , 2011-2012 年是流感高发季, 但我国老年人流感疫苗的接种率仅有 4.3%. 文献[15 ]研究表明, 目前我国流感疫苗接种率维持较低的水平, 流感疫苗接种工作未能有效开展; 加之人们对流感及其并发症危害了解甚少, 面对流感往往不能及时就医, 因此, 往往接种流感疫苗和实施治疗不一定同步进行. 为评价流感最优控制策略, 我们考虑无控制、只接种疫苗、只实施治疗、接种疫苗和治疗同时实施四种情况.
观察图2(b) , 比较四种策略, 我们发现流感传播模式基本相同, 即流感患者都经历峰值后, 最终趋于低流行水平. 只引入一种控制措施与无控制相比较, 发现接种疫苗或实施治疗都能减小流感患者峰值, 且缩短急性暴发期. 比较接种和实施治疗的对流感的影响, 不难发现: 接种后感染峰值低于治疗后感染峰值, 但接种疫苗疫情急性暴发周期较长. 因此, 实施接种长期效果显著, 及时治疗短期效果明显. 比较混合策略和其他策略, 混合策略下染病峰值最低, 约为其他策略峰值的1/4, 且最终流行规模最小. 因此, 混合控制策略效果最佳.
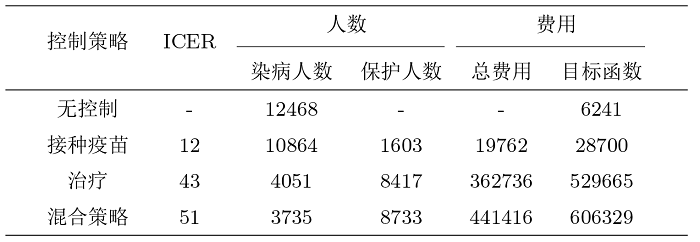
为了定量比较各控制效果, 评估各策略的有效性, 定义增量成本效益比 (ICER) 为
$\textrm{ICER}=\frac{\textrm{两种策略的总费用之差}}{\textrm{两种策略未染病人数之差}}.$
表1 从染病者人数、目标函数值、避免染病人数、总费用、ICER 五个方面定量评价四种不同策略下控制效果. 从表1 可以看出: 从无控制到引入混合控制, 染病者总数逐渐减少, 避免染病人数逐渐增加, 表明公共卫生收益排序为: 混合策略 $ > $ $ > $ $ > $ $ > $ $ > $
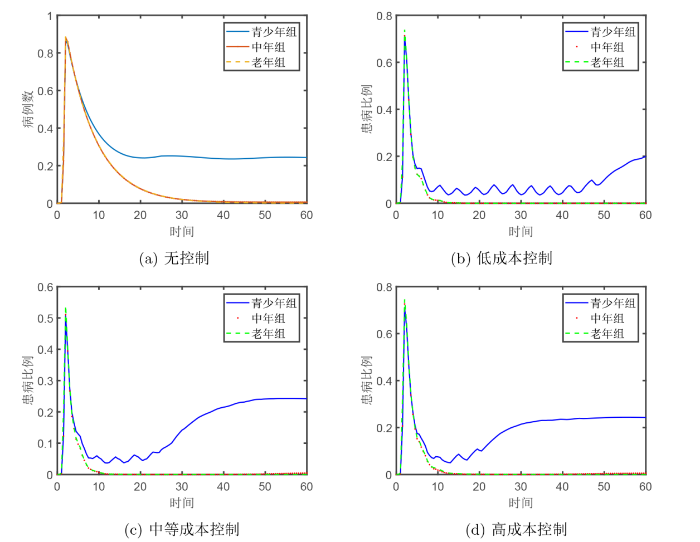
接下来探究策略成本对控制效果的影响. 假设实施混合策略控制流感传播, 固定 $ A_0=1 $ $ A_1=B_1=75, $ $ A_1=B_2=650 $ $ A_1=B_1=7500, $ $ A_1=B_2=65000 $ $ A_1=B_1=75000, $ $ A_1=B_2=650000 $ 图3 给出了青少年组、中年组、老年组人群在不同控制成本效应下染病者人数随时间的变化趋势. 图3 表明: 在不同成本控制下, 流感传播模式相仿, 首先经历一个高峰, 随后递减, 最后进入低流行期; 中年组和老年组患者传播模式几乎相同, 而青少年组在经历峰值下降后会略有上升, 达到一个较高的流行水平. 流感传播呈现出明显的年龄异质性. 实施控制可有效减小各年龄段流感峰值, 且到达到峰值后, 染病者数量的衰减速率更快. 表2 给出定量评判各成本效应指标, 随着成本的提高, 染病者总数、目标函数值、总费用增长明显, 表明公共卫生收益和成本效率都在降低. 因此综合考虑, 低成本控制更有利于流感控制.
图3
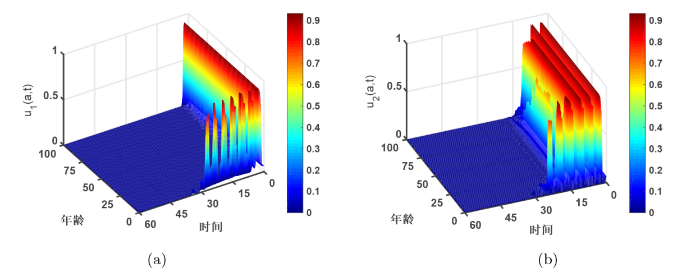
综上所述, 同时引入疫苗和治疗, 并以低成本控制流感效果最佳. 图4 给出最优控制对 $ (u_1,u_2) $
图4
图4
(a) 接种最优控制; (b) 治疗最优控制
在年龄维度上, 实施治疗和疫苗接种贯穿于所有年龄段, 特别要加强青少年的接种力度.
5 结论
本文考虑流感传播机理和流感的年龄异质性, 构建连续年龄结构流感模型. 利用庞特利亚金最大值原理及 Ekland 变分原理得到最优控制问题解存在唯一性. 通过数值模拟的方法, 对比无控制、单一控制和混合控制下的染病者人数和多种评价指标, 得出治疗短期效果突出、接种疫苗长期效果更佳、接种疫苗和治疗组合实施最有效的结论. 在接种疫苗和治疗组合实施的基础上, 探究不同等级的控制成本对流感控制的影响. 我们发现低成本的控制效果最好; 在资源有限的情况下, 最优控制策略应在不同年龄段及时间段采用不同的控制策略, 即流感爆发前期要加大疫苗接种和流感治疗的强度, 特别要提高 0-25 岁人群的疫苗接种比例及提升治疗方案或措施.
参考文献
View Option
[1]
Li X Z Yang J Y Martcheva M . Age Structured Epidemic Modeling . Switzerland : Springer Nature , 2020
[本文引用: 1]
[2]
凌云 , 狄亚敏 , 陆青青 , 李烁 . 流行性感冒的病原学特征及其药物治疗进展
解放军药学学报 , 2018 , 34 02 ): 159 -164
[本文引用: 1]
Ling Y Di Y M Lu Q Q Li S . Pathogenic characteristics of influenza and its drug treatment progress
Pharm J Chin PLA , 2018 , 34 2 ): 159 -164
[本文引用: 1]
[3]
罗道清 . 接种流感疫苗对流感疾病的预防控制作用分析
临床医学工程 , 2020 , 27 08 ): 1035 -1036
[本文引用: 1]
Luo D Q . Analysis of prevention and control effect of influneza vaccination on influenza diseases
Clinical Medicine & Engineering , 2020 , 27 08 ): 1035 -1036
[本文引用: 1]
[4]
Matrajt L Longini Jr I M . Optimizing vaccine allocation at different points in time during an epidemic
PLoS One , 2010 , 5 11 ): e13767
[本文引用: 1]
[5]
Nuno M Castillo-Chavez C Feng Z Martcheva M . Mathematical models of influenza: The role of cross-immunity, quarantine and age-structure //Brauer F, van den Driessche P, Wu J, eds. Mathematical Epidemiology. Lecture Notes in Mathematics, vol 1945. Heidelberg : Springer , 2008 : 349 -364
[本文引用: 1]
[6]
Patel R Longini I M Jr Halloran M E . Finding optimal vaccination strategies for pandemic influenza using genetic algorithms
Journal of Theoretical Biology , 2005 , 234 201 -212
PMID:15757679
[本文引用: 1]
In the event of pandemic influenza, only limited supplies of vaccine may be available. We use stochastic epidemic simulations, genetic algorithms (GA), and random mutation hill climbing (RMHC) to find optimal vaccine distributions to minimize the number of illnesses or deaths in the population, given limited quantities of vaccine. Due to the non-linearity, complexity and stochasticity of the epidemic process, it is not possible to solve for optimal vaccine distributions mathematically. However, we use GA and RMHC to find near optimal vaccine distributions. We model an influenza pandemic that has age-specific illness attack rates similar to the Asian pandemic in 1957-1958 caused by influenza A(H2N2), as well as a distribution similar to the Hong Kong pandemic in 1968-1969 caused by influenza A(H3N2). We find the optimal vaccine distributions given that the number of doses is limited over the range of 10-90% of the population. While GA and RMHC work well in finding optimal vaccine distributions, GA is significantly more efficient than RMHC. We show that the optimal vaccine distribution found by GA and RMHC is up to 84% more effective than random mass vaccination in the mid range of vaccine availability. GA is generalizable to the optimization of stochastic model parameters for other infectious diseases and population structures.
[7]
邱守中 , 潘利花 , 梁夏楠 , 等 . 流感疫苗接种对儿童流感预防的有效性与安全性分析
医学动物防制 , 2022 , 38 05 ): 505 -506
[本文引用: 1]
Qiu S Z Pan L H Liang X N , et al . Analysis on efficacy and safety of inluenza vaccination against influence in children
Journal of Medical Pest Control , 2022 , 38 05 ): 505 -506
[本文引用: 1]
[8]
Read J M Lessler J Riley S , et al . Social mixing patterns in rural and urban areas of southern China . Proceedings of the Royal Society B : Biological Sciences , 2014 , 281 1785 ): 20140268
[本文引用: 1]
[9]
随海田 , 郭洋 , 赵杰 , 等 . 流感疫苗在高危人群中应用安全性、有效性及接种现状研究新进展
中华流行病学杂志 , 2022 , 43 3 ): 436 -439
DOI:10.3760/cma.j.cn112338-20210227-00153
PMID:35345303
[本文引用: 1]
This paper reviews the domestic and foreign studies published in 2020 on the application of influenza vaccine in populations at high risk. The importance of influenza vaccination in population at high risk has been proved by larger sample, multicentre, high-quality evidence-based studies. Influenza vaccination is the most cost-effective measure to prevent influenza. However, the coverage rate of influenza vaccine is very low in China, it is necessary to strengthen the health education to promote influenza vaccination in different populations. It is recommended to give influenza vaccination to the population in whom influenza vaccination has been proven safe and effective before influenza season. Research of the safety, efficiency and cost-effectiveness of influenza vaccine should be accelerated for the populations in whom such data are lacking or insufficient.
Sui H T Guo Y Zhao J , et al . New progress in research on the safety, effectiveness, and vaccination status of influenza vaccines in high-risk populations
Chinese Journal of Epidemiology , 2022 , 43 3 ): 436 -439
DOI:10.3760/cma.j.cn112338-20210227-00153
PMID:35345303
[本文引用: 1]
This paper reviews the domestic and foreign studies published in 2020 on the application of influenza vaccine in populations at high risk. The importance of influenza vaccination in population at high risk has been proved by larger sample, multicentre, high-quality evidence-based studies. Influenza vaccination is the most cost-effective measure to prevent influenza. However, the coverage rate of influenza vaccine is very low in China, it is necessary to strengthen the health education to promote influenza vaccination in different populations. It is recommended to give influenza vaccination to the population in whom influenza vaccination has been proven safe and effective before influenza season. Research of the safety, efficiency and cost-effectiveness of influenza vaccine should be accelerated for the populations in whom such data are lacking or insufficient.
[10]
向蓥飞 , 周德谦 , 钟杰伟 , 等 . 广州市越秀区托幼机构流感样病例暴发疫情经济负担评估和流感疫苗卫生经济学评价
华南预防医学 , 2021 , 47 10 ): 1231 -1235
[本文引用: 1]
Xiang Y F Zhou D Q Zhong W J , et al . Evaluation of the economic burden of influenza like cases outbreak and health economics of influenza vaccines in nursery and child care institutions in Yuexiu district, Guangzhou city
South China Journal of Preventive Medicine , 2021 , 47 10 ): 1231 -1235
[本文引用: 1]
[11]
张春国 . 流行性感冒的药物治疗分析
世界最新医学信息文摘 , 2015 , 15 18 ): 78
[本文引用: 1]
Zhang C G . Analysis of drug therapy for influenza
World Latest Medicne Information , 2015 , 15 18 ): 78
[本文引用: 1]
[12]
赵宏婷 , 范思萌 , 杨孝坤 , 等 . 季节性流感在不同年龄人群中的临床特征及严重程度研究概述
国际病毒学杂志 , 2021 , 28 05 ): 424 -427
[本文引用: 1]
Zhao H T Fan S M Yang X K , et al . Review of clinical characteristics and severity of seasonal influenza in different age groups
International Journal of Virology , 2021 , 28 05 ): 424 -427
[本文引用: 1]
[13]
赵双雨 , 董书衡 , 李欣辰 , 等 . 中国流感疫苗优先推荐接种人群疫苗犹豫现状及影响因素
中国预防医学杂志 , 2021 , 22 10 ): 798 -803
[本文引用: 2]
Zhao S Y Dong S H Li X C , et al . The current situation and influencing factors of hesitancy in recommending influenza vaccines to priority recipients in China
Chin Prev Med , 2021 , 22 10 ): 789 -803
[本文引用: 2]
[14]
中国公共卫生科学数据中心 . https://www.phsciencedata.cn/Share/kysjml.jsp?id=c6f2fbd7-a11a-426f-b9fb-fa3ce0c1b8b4
URL
[本文引用: 1]
[15]
Zhou L Su Q Xu I , et al . Seasonal influenza vacation coverage rate of target groups in selected cities and provinces in China by season(20009/10 to 2011/12)
PLoS One , 2013 , 8 9 ): e73724
[本文引用: 1]
[16]
http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm. [2023 -04 -01 ]
URL
[本文引用: 1]
1
2020
... 方程(2.2)是一个经典的 Mckendrick-Von Foester 方程. 由文献[1 ]知, 存在一个稳态分布 ...
流行性感冒的病原学特征及其药物治疗进展
1
2018
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
流行性感冒的病原学特征及其药物治疗进展
1
2018
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
接种流感疫苗对流感疾病的预防控制作用分析
1
2020
... 流行性感冒是由流感病毒所致的感染, 主要通过日常的接触传染. 流感的传染能力强, 并且流感病毒变异速度快, 人群缺乏普适免疫力. 尤其是幼儿和老年人等免疫系统较弱的人群, 感染流感病毒后容易发展成为重症病例. 每年约有 250, 000-500, 000人死于流感. 人类在感染流感后一周, 体内会产生流感抗体, 并且该抗体在短期内不会消失. 在同一流感流行季, 具有流感抗体的人群对流感具有一定的免疫力, 不会再次感染同类型的流感病毒. 接种疫苗和流感治疗是抑制流感传染的两种有效方法. 甲型 H3N2 亚型及乙型 Yamagata 系疫苗可有效降低接种者罹患流感和严重并发症的风险. 奥司他韦、扎那米韦等神经氨酸酶抑制剂是甲型和乙型流感的有效治疗药物, 能显著降低流感重症和死亡的发生率. 罗道清[3 ] 发现接种流感疫苗能有效降低发生率及并发症. ...
接种流感疫苗对流感疾病的预防控制作用分析
1
2020
... 流行性感冒是由流感病毒所致的感染, 主要通过日常的接触传染. 流感的传染能力强, 并且流感病毒变异速度快, 人群缺乏普适免疫力. 尤其是幼儿和老年人等免疫系统较弱的人群, 感染流感病毒后容易发展成为重症病例. 每年约有 250, 000-500, 000人死于流感. 人类在感染流感后一周, 体内会产生流感抗体, 并且该抗体在短期内不会消失. 在同一流感流行季, 具有流感抗体的人群对流感具有一定的免疫力, 不会再次感染同类型的流感病毒. 接种疫苗和流感治疗是抑制流感传染的两种有效方法. 甲型 H3N2 亚型及乙型 Yamagata 系疫苗可有效降低接种者罹患流感和严重并发症的风险. 奥司他韦、扎那米韦等神经氨酸酶抑制剂是甲型和乙型流感的有效治疗药物, 能显著降低流感重症和死亡的发生率. 罗道清[3 ] 发现接种流感疫苗能有效降低发生率及并发症. ...
Optimizing vaccine allocation at different points in time during an epidemic
1
2010
... 但由于医疗资源的有限性及流感疫苗免疫能力的局限性, 利用有限资源使利益最大化是政府及决策者的理想选择. 以利益为出发点, 许多学者考虑最佳年龄接种分配方案、最小化感染病例或死亡病例等一系列最优控制策略[4 ,6 ] . 大多数模型都假设人群是均匀混合的和人的年龄无关, 不能精准捕捉流感传播的年龄异质性. 为此, 我们提出一类具有连续年龄结构的流感模型, 综合评估最优接种及治疗策略. 年龄结构传染病模型最优控制问题本质上属于$ L^1 $
1
2008
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
Finding optimal vaccination strategies for pandemic influenza using genetic algorithms
1
2005
... 但由于医疗资源的有限性及流感疫苗免疫能力的局限性, 利用有限资源使利益最大化是政府及决策者的理想选择. 以利益为出发点, 许多学者考虑最佳年龄接种分配方案、最小化感染病例或死亡病例等一系列最优控制策略[4 ,6 ] . 大多数模型都假设人群是均匀混合的和人的年龄无关, 不能精准捕捉流感传播的年龄异质性. 为此, 我们提出一类具有连续年龄结构的流感模型, 综合评估最优接种及治疗策略. 年龄结构传染病模型最优控制问题本质上属于$ L^1 $
流感疫苗接种对儿童流感预防的有效性与安全性分析
1
2022
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
流感疫苗接种对儿童流感预防的有效性与安全性分析
1
2022
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
1
2014
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
流感疫苗在高危人群中应用安全性、有效性及接种现状研究新进展
1
2022
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
流感疫苗在高危人群中应用安全性、有效性及接种现状研究新进展
1
2022
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
广州市越秀区托幼机构流感样病例暴发疫情经济负担评估和流感疫苗卫生经济学评价
1
2021
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
广州市越秀区托幼机构流感样病例暴发疫情经济负担评估和流感疫苗卫生经济学评价
1
2021
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
流行性感冒的药物治疗分析
1
2015
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
流行性感冒的药物治疗分析
1
2015
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
季节性流感在不同年龄人群中的临床特征及严重程度研究概述
1
2021
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
季节性流感在不同年龄人群中的临床特征及严重程度研究概述
1
2021
... 许多学者利用不同的方法探讨流感传播的年龄异质性. 赵宏婷等[12 ] 对季节性流感在儿童、成人和老年人群中的临床差异和严重程度差别等研究进行了归纳和分析. 文献[7 ,9 ]研究表明接种流感疫苗能有效降低幼儿、老人等免疫力较弱人群产生严重的并发症, 甚至死亡的概率. 流感病毒变异快, 疫苗产生的免疫作用有限, 不足以抵御所有流感病毒的侵害. 文献[2 ,11 ]分析了流行性感冒的药物治疗程序及效率, 发现在 48 小时内接受药物治疗能缓减症状、缩短病程及降低死亡率. Nuno 等[5 ] 建立年龄结构流感模型并讨论其动力学行为. ...
中国流感疫苗优先推荐接种人群疫苗犹豫现状及影响因素
2
2021
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
... 另外, 据调查研究[13 ] , 2011-2012 年是流感高发季, 但我国老年人流感疫苗的接种率仅有 4.3%. 文献[15 ]研究表明, 目前我国流感疫苗接种率维持较低的水平, 流感疫苗接种工作未能有效开展; 加之人们对流感及其并发症危害了解甚少, 面对流感往往不能及时就医, 因此, 往往接种流感疫苗和实施治疗不一定同步进行. 为评价流感最优控制策略, 我们考虑无控制、只接种疫苗、只实施治疗、接种疫苗和治疗同时实施四种情况. ...
中国流感疫苗优先推荐接种人群疫苗犹豫现状及影响因素
2
2021
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
... 另外, 据调查研究[13 ] , 2011-2012 年是流感高发季, 但我国老年人流感疫苗的接种率仅有 4.3%. 文献[15 ]研究表明, 目前我国流感疫苗接种率维持较低的水平, 流感疫苗接种工作未能有效开展; 加之人们对流感及其并发症危害了解甚少, 面对流感往往不能及时就医, 因此, 往往接种流感疫苗和实施治疗不一定同步进行. 为评价流感最优控制策略, 我们考虑无控制、只接种疫苗、只实施治疗、接种疫苗和治疗同时实施四种情况. ...
1
... 流感传播具有明显的年龄异质性. 图1(a) 给出 2017 年中国流感年龄分布数据[14 ] . 在三个年龄组中, 青少年流感患者普遍偏多, 老年患者最少且分布较平均; 图1(b) 直观地展现了各年龄组染病者占比. 发现大多数月份青少年患者占比超 50%, 少数月份青少年患者和中年患者占比相近, 老年患者占比约为 5%-10%. 因此, 辨识年龄异质性对流感传播的影响关键因素, 对于预防与控制流感传播至关重要. ...
Seasonal influenza vacation coverage rate of target groups in selected cities and provinces in China by season(20009/10 to 2011/12)
1
2013
... 另外, 据调查研究[13 ] , 2011-2012 年是流感高发季, 但我国老年人流感疫苗的接种率仅有 4.3%. 文献[15 ]研究表明, 目前我国流感疫苗接种率维持较低的水平, 流感疫苗接种工作未能有效开展; 加之人们对流感及其并发症危害了解甚少, 面对流感往往不能及时就医, 因此, 往往接种流感疫苗和实施治疗不一定同步进行. 为评价流感最优控制策略, 我们考虑无控制、只接种疫苗、只实施治疗、接种疫苗和治疗同时实施四种情况. ...
1
2023
... 本节将利用数值模拟评估控制策略的有效性. 文献[16 ]可确定出生率函数 $ \beta(a) $ $ \mu(a) $ $ \gamma(a)=1/7. $ 8 ], 接触矩阵 $ k(a,b) $ 图2(a) . 文献[10 ,13 ]表明流感疫苗接种单价为 75 元, 流感治疗单价为 650 元, 因此我们固定 $ A_0=1, $ $ A_1=B_1=75, $ $ A_2=B_2=650. $
