1 引言
随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下
(1.1) $ u_{t}+6\sigma u^{2}u_{x}+ u_{xxx}=0,$
其中 $\sigma=\pm1$, $u=u(x,t)$ 是关于空间变量 $x$ 和时间变量 $t$ 的实函数. 方程 (1.1) 在众多的物理情形下具有重要应用, 例如: 光纤中超连续谱的产生[7 ] 、 晶格中孤子的传播[8 ] 、等离子体中非线性 Alfvén 波的传播[9 ] . 当考虑高阶色散时, 可以得到阶数更高的方程[10 ] . 经典的五阶 mKdV 方程具有如下形式
(1.2) $ u_{t}+(6u^{5}+10\sigma uu_{x}^{2}+10\sigma u^{2}u_{xx}+ u_{xxxx})_{x}=0.$
从方程 (1.2) 及其拉格朗日量出发, 可以导出聚焦形式下包含非线性项 $u^{2}u_{xx}$ 和三阶色散项 $u_{xxx}$ 的扩展的五阶 mKdV (extended mKdV, emKdV) 方程[11 ],[12 ],[13 ] , 即
(1.3) $ u_{t}+\alpha(6 u^{2}u_{x}+u_{xxx})+\beta(6u^{5}+10 uu_{x}^{2}+10 u^{2}u_{xx}+ u_{xxxx})_{x}=0,$
其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题.
近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升.
目前针对 PINNs 算法的研究不仅在经验上取得了成功, 在理论分析上也有显著成果. Jin 等[27 ] 从数据分布和神经网络光滑性的角度研究了分类问题中神经网络的泛化误差; Lu 等[28 ] 从宏观角度对 PINNs 的近似理论及误差来源做了简要分析; Wang 等[29 ] 则从神经正切核的角度分析了 PINNs 的训练动态, 并证明了全连接神经网络损失函数不同分量的收敛速度存在差异; Son 等[30 ] 提出了收敛速度更快的 Sobolev-PINNs, 并从理论上证明了改进后的损失函数可以保证神经网络在相应的 Sobolev 空间中收敛到方程的解.
上述专家学者的工作为研究非线性方程提供了众多值得借鉴、推广的经验和方法, 本文预将深度学习方法推广到狄利克雷边界条件下方程 (1.3) 正反问题的求解中. 本文的结构安排如下: 第二部分以一般的五阶非线性演化方程为例, 介绍 PINNs 深度学习方法求解 PDE 正反问题的主要步骤; 第三部分借助简化的 Hirota 方法给出五阶 emKdV 方程 (1.3) 孤子解的表达式, 并利用 PINNs 方法求解方程的一、二、三孤子解, 对孤子的动力学行进行分析、模拟; 第四部分基于方程的一、二、三孤子解数据, 反求方程的两个待定系数, 并探究不同强度的高斯噪声干扰对 PINNs 算法的影响; 最后在第五部分作了简要总结.
2 物理信息神经网络求解微分方程
对于如下某些物理信息 (初值、边界和一些额外的信息) 已知的 (1+1)-维五阶非线性演化方程
(2.1) $ \left\{\begin{array}{ll}u_{t}=\mathcal N(u,u_{x},u_{xx},u_{xxx},u_{xxxx},u_{xxxxx};\boldsymbol{\lambda}),&x\in[x_{0},x_{p}],t\in[t_{0},t_{q}],\\u(x,t_{0})=\mathcal I(x,t_{0}),&x\in[x_{0},x_{p}],\\u(x_{0},t)=a,u(x_{p},t)=b,&t\in[t_{0},t_{q}],\\u(x,t^{\prime})=u_{\Omega}(x,t^{\prime}), &x\in[x_{0},x_{p}],t^{\prime}\in(t_{0},t_{q}],\end{array}\right.$
其中 $x$ 和 $t$ 分别代表空间和时间; $\mathcal N$ 不仅是 $u(x,t)$ 关于空间变量 $x$ 的导数的非线性函数, 而且是关于反问题待求系数 $\boldsymbol{\lambda}=\lbrace \lambda_1,\lambda_2,\cdots \rbrace$ 的非线性算子, 在考虑正问题时, $\boldsymbol{\lambda}$ 是已知的; $\mathcal I(x,t)$ 是已知的实值光滑函数, $a$ 和 $b$ 为常数; 在考虑反问题时, 我们还知道方程在区域 $\Omega \subset [x_{0},x_{p}] \times (t_{0},t_{q}]$ 内一些观测点处的精确解 $u_{\Omega}(x,t)$.
本章节中主要介绍如何通过多层神经网络求解方程 (2.1) 潜在的解, 以及如何利用已知信息求解方程的系数 $\boldsymbol{\lambda}$. 首先建立神经网络, 然后给出损失函数的定义, 通过极小化损失函数不断更新神经网络的参数, 当网络参数达到最优时输出当前的预测结果. PINNs 求解方程的示意图如图 1 所示
图 1
图 1
物理信息神经网络求解 (1+1) 维五阶非线性演化方程的示意图
2.1 建立神经网络
构建包含一个输入层、$N-1$ 个隐藏层以及一个输出层的全连接神经网络, $x$ 和 $t$ 分别作为网络的输入. 假设隐藏层的第 $j$ 层有 $k$ 个神经元, 则第 $j$ 层将获得第 $j-1$ 层的输出 $\mathbf{x}_{j-1}$ 作为输入, 即
(2.2) $ \begin{aligned}\text{输入层:}\qquad&\mathbf{x}_{0}= \{x;t\},\\\text{隐藏层:}\qquad&\mathbf{x}_{j}=\sigma(\mathbf {W}_{j} \mathbf{x}_{j-1}+\mathbf{b}_{j}),j=1,2,\cdots,N-1,\\\text{输出层:}\qquad&\hat{u}=\mathbf {W}_{j}\mathbf{x}_{j-1}+\mathbf {b}_{j},j=N,\\\end{aligned}$
其中 $\sigma$ 为非线性激活函数, 用于隐藏层单元的计算. 常见的激活函数包括 ReLU、sigmoid、tanh 等. $\mathbf {W}_{j}$ 和 $\mathbf{b}_{j}$ 分别为第 $j$ 层的权重和偏置, 其中 $\mathbf {W}_{1} \in \mathbb{R}^{k \times 2}$, $\mathbf {W}_{j} \in \mathbb{R}^{k \times k} (j=2,\cdots,N-1)$, $\mathbf {W}_{N} \in \mathbb{R}^{k}$, $\mathbf {b}_{j} \in \mathbb{R}^{k} (j=1,2,\cdots,N-1)$, $\mathbf {b}_{N} \in \mathbb{R}$. 神经网络每完成一次训练, 参数 $\boldsymbol{\theta}=\lbrace \mathbf {W}_{j},\mathbf{b}_{j}\rbrace_{j=1}^{N}$ 也随之更新一次. 在求解反问题时, $\boldsymbol{\lambda}$ 只是一个待优化的参数, 并不作为神经网络的输入.
2.2 定义损失函数
预测值和真实值之间的损失一部分来源于神经网络拟合方程本身时的损失; 另一部分来源于神经网络拟合初值、边界条件等信息带来的损失. 对方程本身 (区域内部的配置点) 而言, 引入残差
(2.3) $ \mathcal R_{\boldsymbol{\theta}}(x,t)=\hat{u}_{t}-\mathcal N(\hat{u},\hat{u}_{x},\hat{u}_{xx},\hat{u}_{xxx},\hat{u}_{xxxx},\hat{u}_{xxxxx};\boldsymbol{\lambda}),$
其中 $\boldsymbol{\theta}$ 是包含权重项和偏置项的向量. 定义损失函数
(2.4) $ \begin{split}\left\{\begin{array}{l} \mathcal L_{\mathcal R}(\boldsymbol{\theta};\boldsymbol{\lambda})=\frac{1}{N_{\mathcal R}} \sum\limits_{j=1}^{N_{\mathcal R}} \left| \mathcal R_{\boldsymbol{\theta}}(x_{\mathcal R}^{j},t_{\mathcal R}^{j})\right|^2,\\[4mm] \mathcal L_{\mathcal I}(\boldsymbol{\theta};\boldsymbol{\lambda})=\frac{1}{N_{\mathcal I}} \sum\limits_{j=1}^{N_{\mathcal I}} \left| \hat{u}(x_{\mathcal I}^{j},t_{0})-{\mathcal I}^{j}\right|^2,\\[4mm] \mathcal L_{\mathcal B}(\boldsymbol{\theta};\boldsymbol{\lambda})=\frac{1}{N_{\mathcal B}} \sum\limits_{j=1}^{N_{\mathcal B}} \left| \hat{u}(x_{\mathcal B}^{j},t_{\mathcal B}^{j})-{\mathcal B}^{j}\right|^2,\\[4mm] \mathcal L_{\Omega}(\boldsymbol{\theta};\boldsymbol{\lambda})=\frac{1}{N_{\Omega}} \sum\limits_{j=1}^{N_{\Omega}} \left| \hat{u}(x_{\Omega}^{j},t_{\Omega}^{j})-{\Omega}^{j}\right|^2,\end{array}\right.\end{split}$
其中, $\mathcal L_{\mathcal R}(\boldsymbol{\theta};\boldsymbol{\lambda})$ 表示 PDE 残差的损失, $\mathcal L_{\mathcal I}(\boldsymbol{\theta};\boldsymbol{\lambda})$ 和 $\mathcal L_{\mathcal B}(\boldsymbol{\theta};\boldsymbol{\lambda})$ 分别表示初始条件和边界条件的损失, $\mathcal L_{\Omega}(\boldsymbol{\theta};\boldsymbol{\lambda})$ 表示区域 $\Omega$ 内已知信息点处的损失. $N_{\mathcal R}$, $N_{\mathcal I}$, $N_{\mathcal B}$ 和 $N_{\Omega}$ 分别代表内部配置点、初始和边界取点, 以及额外观测点的数目. $\left\{ {x_{\mathcal R}^{j},t_{\mathcal R}^{j}} \right\}$ 表示用于极小化 PDE 残差的配置点; $\left\{ {x_{\mathcal I}^{j},t_{0},{\mathcal I}^{j}} \right\} _{j=1}^{N_{\mathcal I}}$ 和 $ \left\{ {x_{\mathcal B}^{j},t_{\mathcal B}^{j},{\mathcal B}^{j}} \right\}_{j=1}^{N_{\mathcal B}}$ 分别代表初始训练集和边界训练集; 在求解反问题时, $\left\{ {x_{\Omega}^{j},t_{\Omega}^{j}} \right\}$ 代表额外的观测点, 通过这些点处的信息可以更加准确地识别待求的方程系数 $\boldsymbol{\lambda}$.
2.3 极小化损失函数
为了使预测结果与精确值之间的误差尽可能小, 还需要极小化损失函数, 这也是优化的目标所在, 即
(2.5) $ \min \mathcal L(\boldsymbol{\theta};\boldsymbol{\lambda})=\min [ \mathcal L_{\mathcal R}(\boldsymbol{\theta};\boldsymbol{\lambda})+\mathcal L_{\mathcal I}(\boldsymbol{\theta};\boldsymbol{\lambda})+\mathcal L_{\mathcal B}(\boldsymbol{\theta};\boldsymbol{\lambda})+\mathcal L_{ \Omega}(\boldsymbol{\theta};\boldsymbol{\lambda})].$
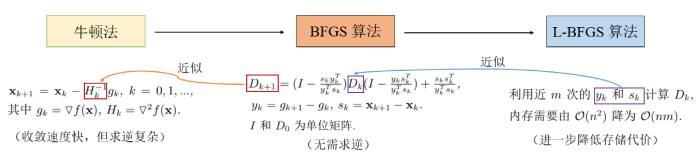
机器学习中解决优化问题常用的算法主要有牛顿法、梯度下降法、Adam 和 L-BFGS 优化算法. 本文主要使用 L-BFGS (Limited-memory BFGS) 优化器来对损失函数进行优化. L-BFGS 算法[31 ] 是一种基于二阶梯度来寻找目标函数最优值的拟牛顿优化算法, 其基本思想是只保存迭代过程中近 $m$ 次的迭代信息, 从而减少数据存储空间, 提升计算效率. 下面我们以一般的优化问题为例, 介绍牛顿法、BFGS 算法和 L-BFGS 算法的联系与区别. 假设多元函数优化问题的目标为 $\arg \min \limits_{\mathbf{x}} f(\mathbf{x})$, $\mathbf{x} \in \mathbb{R}^{n}$, 牛顿法利用函数 $f(\mathbf{x})$ 的前两项泰勒展开式来寻找方程 $f(\mathbf{x})=0$ 的根, 优点是收敛速度较快, 是一种二阶收敛的算法, 缺点是使用牛顿法需要消耗大量资源计算 Hessian 矩阵的逆 $H^{-1}$; BFGS 算法由牛顿法发展而来, 在继承了牛顿法二阶收敛的同时, 通过迭代计算 Hessian 矩阵的近似逆 $D^{-1}$, 进一步降低了运算成本; L-BFGS 算法可以看作 BFGS 算法的近似, 前者只存储和利用向量序列的部分信息 $\lbrace(\mathbf{x}_{i},\nabla f(\mathbf{x}_{i}))\rbrace_{i=1}^{m}$ 来减少内存花销. 图 2 对比展示了牛顿法、BFGS 算法与 L-BFGS 算法间的关系.
图 2
图 2
牛顿法、BFGS 算法与 L-BFGS 优化算法间的关系示意图.
在接下来的章节中, 我们将利用上述 PINNs 方法数据驱动求解五阶 emKdV 方程 (1.3) 的正反问题. 数值实验表明并不需要非常复杂的网络结构便可获得较好精度的预测结果, 本文选用三个隐藏层, 每层 20 个神经元的全连接神经网络, 并且所有代码都基于 Python 3.8 和 Tensorflow 2.8.0, 所有数值算例都执行于配备 Intel Core i7 处理器和 16 GB 内存的 Lenovo 计算机上.
3 数据驱动求解方程 (正问题)
本节我们使用 PINNs 深度学习方法求解具有如下初值和边界条件的五阶 emKdV 方程
(3.1) $ \left\{\begin{array}{l}u_{t}+\alpha(6 u^{2}u_{x}+u_{xxx})+\beta(6u^{5}+10 uu_{x}^{2}+10 u^{2}u_{xx}+ u_{xxxx})_{x}=0,\\u(x,t_{0})=\mathcal I(x,t_{0}),x\in[x_{0},x_{p}],\\u(x_{0},t)=0,u(x_{1},t)=0,t\in[t_{0},t_{1}].\\\end{array}\right.$
为了衡量预测解的精度, 本文用到的 $L^2$ 相对误差定义如下
(3.2) $ \delta(\mathbf{u},\mathbf{\hat{u}})=\frac{\sqrt{\sum\limits_{i=1}^{n}(u_{i}-\hat{u}_{i})^2}}{\sqrt{\sum\limits_{i=1}^{n}u_{i}^2}},$
其中 $\mathbf{u} \in \mathbb{R}^{n}$ 和 $\mathbf{\hat{u}} \in \mathbb{R}^{n}$ 分别为精确解和预测解构成的列向量, $n$ 的大小取决于数据集在时间方向取点个数与空间方向取点个数的乘积; $u_{i}$ 和 $\hat{u}_{i}$ 代表各自的分量.
下面主要以 $\alpha=0.2$, $\beta=0.04$ 为例, 借助 PINNs 深度学习方法研究方程
(3.3) $ u_{t}+0.2(6 u^{2}u_{xx}+u_{xxx})+0.04(6u^{5}+10 uu_{x}^{2}+10 u^{2}u_{xx}+ u_{xxxx})_{x}=0$
的一、二、三孤子解, 并将数据驱动解与已知精确解进行比较, 从而验证方法的有效性. 对于 $\alpha$ 和 $\beta$ 取其它值时方程的解, 我们也进行了数值模拟.
对照文献 [13 ] 的步骤, 可得方程 (3.3) 一孤子解的表达式为
(3.4) $ u(x,t)=\frac{2k_1e^{\theta_1}}{1+e^{2\theta_1}},$
其中 $\theta_1=k_1x-(0.2 k_1^3+0.04 k_1^5)t$, $k_1$ 为常数. 方程 (3.3) 二孤子解的表达式为
(3.5) $ u(x,t)=-\frac{2(k_{1}e^{\theta_1}+k_{2}e^{\theta_2})(a_{12}e^{\theta_1+\theta_2}-1)-2a_{12}(k_{1}+k_{2})e^{\theta_1+\theta_2}(e^{\theta_1}+e^{\theta_2})}{(a_{12}e^{\theta_1+\theta_2}-1)^2+(e^{\theta_1}+e^{\theta_2})^2},$
其中 $a_{12}=\frac{(k_{1}-k_{2})^2}{(k_{1}+k_{2})^2}$, $\theta_1=k_1x-(0.2 k_1^3+0.04 k_1^5)t$, $\theta_2=k_2x-(0.2 k_2^3+0.04 k_2^5)t$, $k_{1}$ 和 $k_{2}$ 为常数. 方程 (3.3) 三孤子解的表达式为
(3.6) $ u(x,t)=-\frac{X}{Y},$
并且 $a_{pq}=\frac{(k_{p}-k_{q})^2}{(k_{p}+k_{q})^2}$, $1\leq p \leq q \leq 3$; $\theta_i=k_ix-(0.02 k_i^3+0.04 k_i^5)t$, $1\leq i \leq 3$, $k_{i}$ 为常数.
3.1 数据驱动求解一孤子解
在一孤子解 (3.4) 中, 取参数 $k_1=1$, 解的表达式为
(3.7) $ u(x,t)=\frac{2e^{x-0.24t}}{1+e^{2x-0.48t}}.$
对 (3.7) 式在区域 $x\in[-15,15]$, $t\in[-5,5]$ 内进行离散, 获得 512*201 个点的测试数据集. 借助拉丁超立方体抽样方法[32 ] 从上述数据集中抽取 $N_{\mathcal R}=10000$ 个内部配置点用于方程残差的训练; 选取 $N_{\mathcal I}=100$ 和 $N_{\mathcal B}=120$ 个点分别用于初始和边界条件的训练.
图 3
图 3
[$-\pi,\pi$] 区间内五种激活函数的图像.
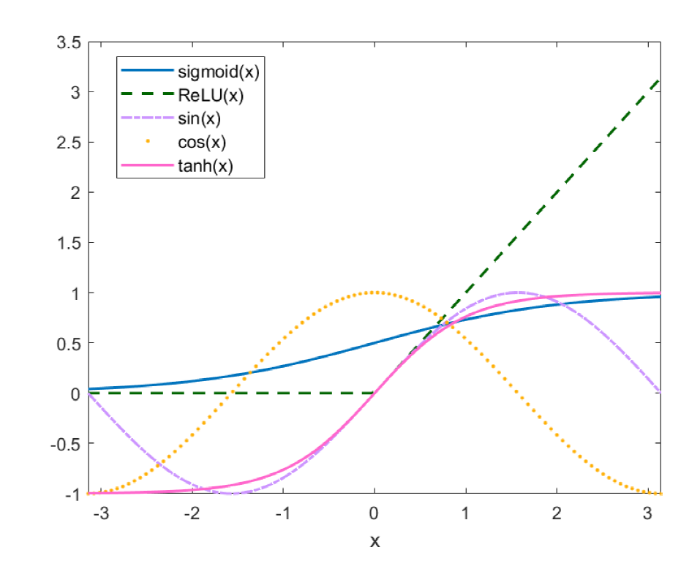
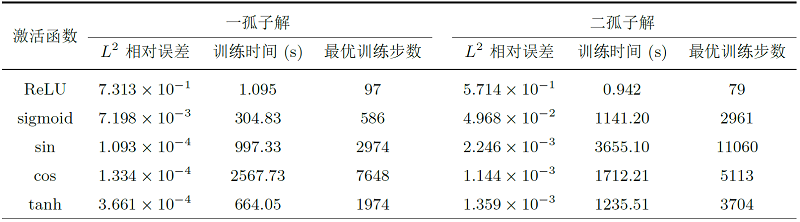
表 1 比较了 ReLU、sigmoid、$\tanh$、$\sin$ 和 $\cos$ 函数 (五种激活函数在区间 [$-\pi,\pi$] 内的函数图像如图 3 所示) 对五阶 emKdV 方程一孤子解进行求解时的预测精度、运行时间和迭代步数, 结果表明: ReLU 激活函数对于当前问题的求解是失效的 (文献 [33 ] 在理论上解释了 ReLU 作为激活函数的神经网络没有办法在 $H^{2}(\Omega)$ 范数下逼近函数); 使用 sigmoid 作为激活函数时, 误差能在非常短的时间达到 $\mathcal{O}(10^{-3})$; 在当前数据集下, 选用双曲正切函数 $\tanh$ 和三角函数 $\sin$、$\cos$ 作为激活函数, 均可使最后的 $L^2$ 相对误差达到 $\mathcal{O}(10^{-4})$, 但是 $\tanh$ 所消耗的时间和训练步数均小于三角函数, 所以本文选用 $\tanh$ 作为激活函数求解 emKdV 方程的一孤子解.
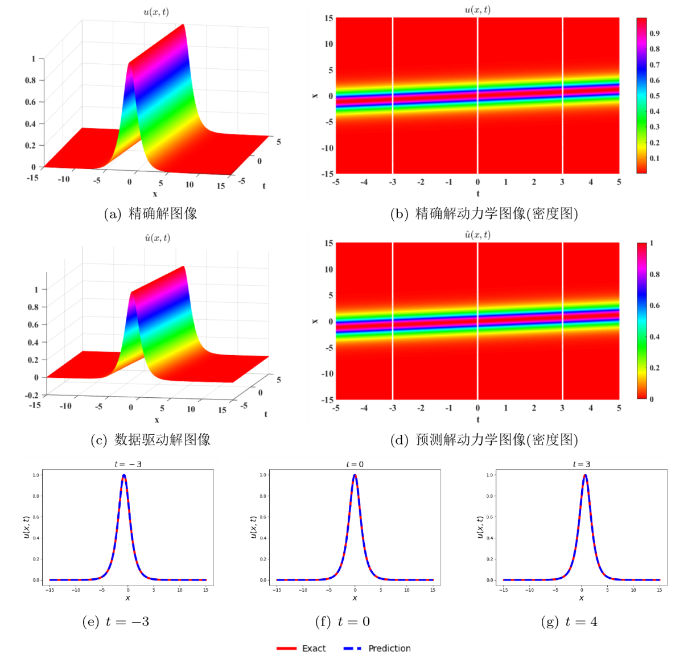
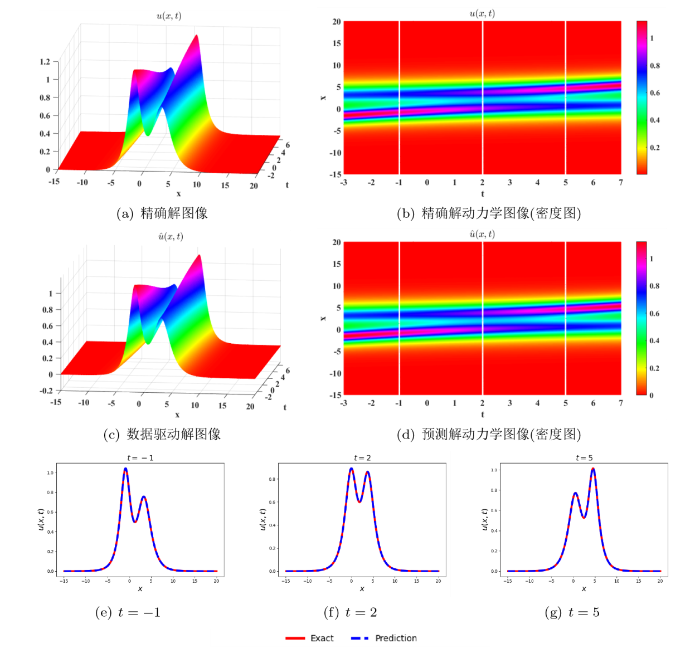
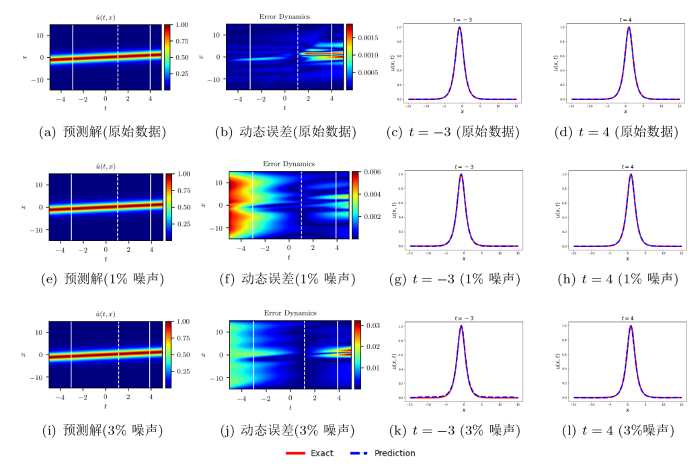
图 4 展示了 PINNs 方法求解方程 (3.3) 一孤子解的运行结果. 方程一孤子解图像以及解的动态变化情况如图 4(a) 和图 4(b) 所示; 一孤子解的形状呈钟状, 且在无穷远处衰减为零, 孤子的传播速度和振幅成正比, 振幅越大, 速度也越高. 图 4(c) 和图 4(d) 分别为预测解的三维图像和密度图; 当前数据驱动解的 $L^2$ 相对误差为 $3.661\times 10^{-4}$, 模型迭代 1974 步达到最优, 训练时长为 $664.05$ 秒; 图 4(e) -图 4(g) 比较了 $t=-3$, $t=0$, $t=3$ 三个时刻精确解与预测解的图像, 两条不同颜色曲线的拟合程度反应了预测精度的好坏.
图 4
图 4
五阶 emKdV 方程的一孤子解. (a) 和 (b): 精确解的三维图像与密度图; (c) 和 (d): 数据驱动解的三维图像和密度图; (e)-(g): $t=-3$, $t=0$, $t=3$ 三个时刻精确解与预测解的比较.
3.2 数据驱动求解二孤子解
在二孤子解 (9) 中, 取参数 $k_1=1.3$, $k_2=0.7$, 解的表达式为
(3.8) $ u(x,t)=-\frac{P}{Q},$
下面将数据驱动求解一孤子解的方法推广到求解二孤子解中. 首先对方程的二孤子解 (12) 在区域 $x\in[-15,20]$, $t\in[-3,7]$ 内进行离散, 获得所需的训练和测试数据. 具体的抽样方法和取点数量与求解一孤子解时相同. 分别使用 ReLU、sigmoid、$\tanh$、$\sin$ 和 $\cos$ 函数对方程 (3.3) 的二孤子解进行求解, 实验数据如表 1 所示. 通过对比, 五种激活函数的表现与求解一孤子解时的结论相似. 综合考虑之下选用 $\tanh$ 作为激活函数求解 emKdV 方程的二孤子解.
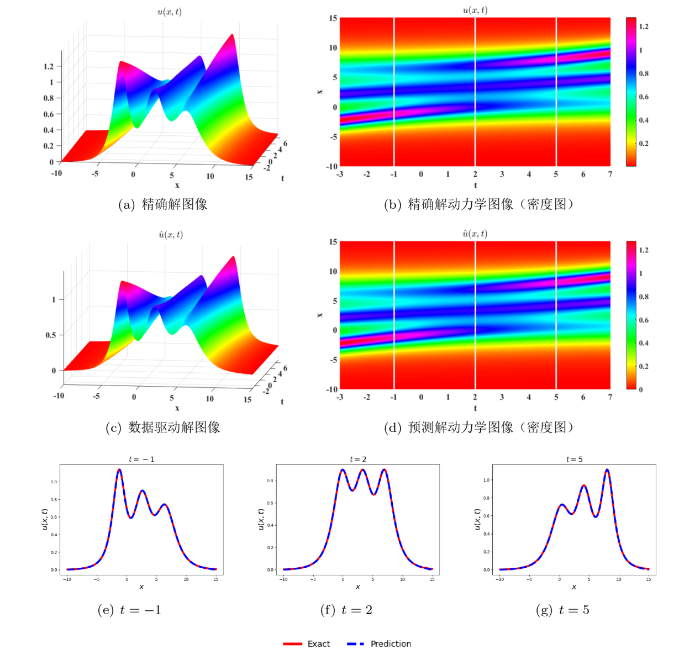
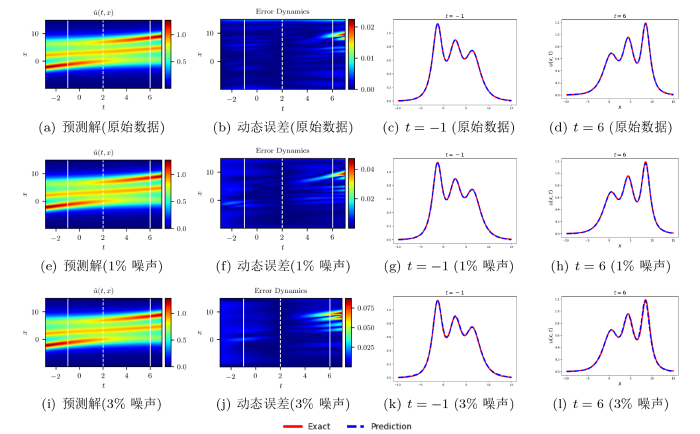
图 5 展示了数据驱动求解五阶 emKdV 方程 (3.3) 二孤子解的运行结果. 方程二孤子解图像以及解的动态变化情况如图 5(a) 和图 5 (ab) 所示: 随着时间的演化, 振幅较高的孤子与振幅较低的孤子发生了相位转换; 除了发生相位转换外, 两个孤子在相互作用后振幅和速度不变, 该类型的孤子也被称为"追赶孤子". 预测解的三维图 5(c) 和密度图 5(d) 准确模拟了孤子相位变化的过程. 当前数据驱动解的 $L^2$ 相对误差为 $1.359\times 10^{-3}$, 模型迭代 3704 步, 总共花费 $1235.51$ 秒. 图 5(e) -图 5(g) 比较了 $t=-1$, $t=2$, $t=5$ 三个时刻精确解与预测解的图像, 图形可见, 孤子自左向右传播, 振幅高的追赶上振幅低的孤子, 然后两者保持原有的速度继续向前传播.
图 5
图 5
五阶 emKdV 方程的二孤子解. (a) 和 (b): 精确解的三维图像与密度图; (c) 和 (d): 数据驱动解的三维图像和密度图; (e)-(g): $t=-1$, $t=2$, $t=5$ 三个时刻精确解与预测解的比较.
3.3 数据驱动求解三孤子解
在三孤子解 (10) 中, 取参数 $k_1=1.5$, $k_2=1.2$, $k_3=0.6$, 解的表达式为
(3.9) $ u(x,t)=-\frac{U}{V},$
对方程的三孤子解 (3.9) 在区域 $x\in[-10,15]$, $t\in[-3,7]$ 内进行离散, 获得所需的测试数据集. 数据的抽样方法和取点数量与求解二孤子解时相同, 选用双曲正切函数 $\tanh$ 作为激活函数. 数据驱动求解五阶 emKdV 方程 (3.3) 三孤子解运行结果如图 6 所示: 三个孤子相互作用并且具有一个共同的作用点, 随着时间的演化, 振幅最高的孤子与振幅最低的孤子发生了相位转换; 除了发生相位转换外, 三个孤子在相互作用后振幅和速度不变. 预测解的三维图 图 6(c) 和密度图 图 6(d) 准确模拟了相位变化的过程. 当前数据驱动解的 $L^2$ 相对误差为 $4.549\times 10^{-3}$, 模型迭代 7054 步, 总共花费 $2982.91$ 秒.
图 6
图 6
五阶 emKdV 方程的三孤子解. (a) 和 (b): 精确解的三维图像与密度图; (c) 和 (d): 数据驱动解的三维图像和密度图; (e)-(g): $t=-1$, $t=2$, $t=5$ 三个时刻精确解与预测解的比较.
双曲正切函数 $\tanh$ 在求解方程一、二、三孤子解时的综合表现如表 2 所示. 通过对运行时间、迭代步数和预测精度进行比较, 不难发现: 在数据驱动求解方程的孤子解时, 随着解的结构变复杂, 计算复杂度也会相应增加, 预测解的精度会随之下降.
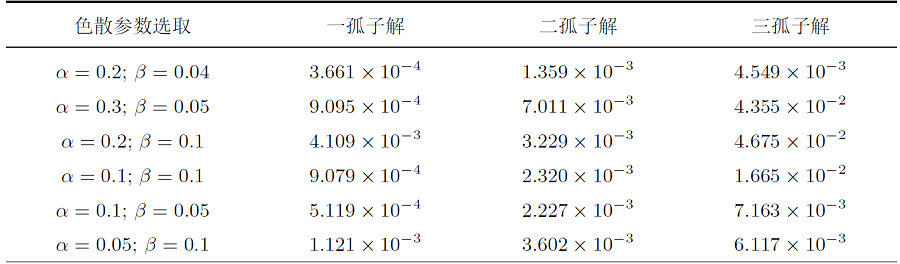
为了验证 PINNs 方法在求解五阶 emKdV 方程正问题中的普适性, 我们使用深度学习方法模拟了方程 (1.3) 中色散系数 $\alpha$ 和 $\beta$ 取不同值时的解. PINNs 求解不同色散系数下五阶 emKdV 方程一、二、三孤子解时的 $L^2$ 相对误差如表 3 所示: 当改变参数 $\alpha$ 和 $\beta$ 的值时, 深度学习方法对于求解方程 (1.3) 的多重孤子解同样是有效的.
4 数据驱动发现方程 (反问题)
根据方程解的信息对神经网络参数进行优化, 从而获得方程系数的预测值, 这个过程也被称为“数据驱动发现方程”. 考虑具有如下初值、边界和观测信息条件的五阶 emKdV 方程
(4.1) $ \left\{\begin{array}{l}u_{t}+0.2(\lambda_1 u^{2}u_{x}+u_{xxx})+0.04(\lambda_1 u^{5}+\lambda_2 uu_{x}^{2}+\lambda_2 u^{2}u_{xx}+ u_{xxxx})_{x}=0,\\u(x,t_{0})=\mathcal I(x,t_{0}),x\in[x_{0},x_{p}],\\u(x_{0},t)=0,u(x_{1},t)=0,t\in[t_{0},t_{1}],\\u(x,t^{\prime})=u_{\Omega}(x,t^{\prime}), x\in[x_{0},x_{p}],t^{\prime}\in(t_{0},t_{q}],\end{array}\right.$
其中 $\boldsymbol{\lambda}=\lbrace \lambda_1,\lambda_2\rbrace$ 为待求的系数, 方程的初始条件 $\mathcal I(x,t_{0})$ 和边界条件已知; 此外, 我们知道方程在 $t=t^{\prime}$ 时刻精确解 $u_{\Omega}(x,t^{\prime})$ 的表达式. 接下来的数值实验中, 在区域 $x\in[x_{0},x_{p}]$, $t\in[t_{0},t_{q}]$ 内部随机抽取 $N_{\mathcal R}=20000$ 个配置点用于方程残差的训练; 选取 $N_{\mathcal I}=200$ 和 $N_{\mathcal B}=100$ 个点, 分别用于初始和边界条件的训练; 在 $t=t^{\prime}$ 时刻等距选取 $N_{\Omega}=101$ 个观测点用于提高模型的预测精度. 赋予待求系数 $\boldsymbol{\lambda}$ 初始猜测值 $\lambda_1=12$, $\lambda_2=2.5$, 并选用 $\tanh$ 作为神经网络的激活函数来逼近方程解以及此时对应的预测系数.
4.1 基于多重孤子解数据驱动求解方程系数
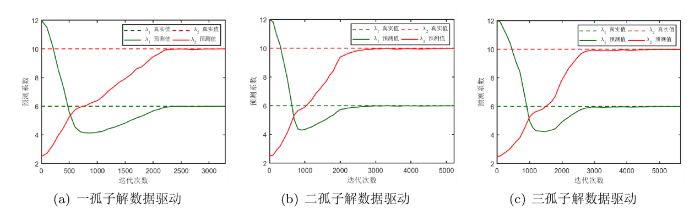
首先, 基于一孤子解 (11) 在区域 $x\in[-15,15]$, $t\in[-5,5]$ 内求解方程 (4.1) 的两个待定系数, 选取 $t^{\prime}=1$ 时刻的观测信息用于模型的校正; 然后, 利用二孤子解 (12) 在区域 $x\in[-15,20]$, $t\in[-3,7]$ 内求解方程的系数, 选取 $t^{\prime}=1$ 时刻的观测信息对模型进行校正; 最后, 利用三孤子解 (13) 在区域 $x\in[-10,15]$, $t\in[-3,7]$ 内求解方程系数, 选取 $t^{\prime}=2$ 时刻的观测信息用于模型的校正. 模型训练过程中, 每进行 100 次迭代输出一次系数的预测值. 待定系数 $\boldsymbol{\lambda}=\lbrace \lambda_1,\lambda_2\rbrace$ 的预测变化曲线如图 7 所示.
图 7
图 7
训练过程中待求系数 $\boldsymbol{\lambda}=\lbrace \lambda_1,\lambda_2\rbrace$ 的预测变化曲线.
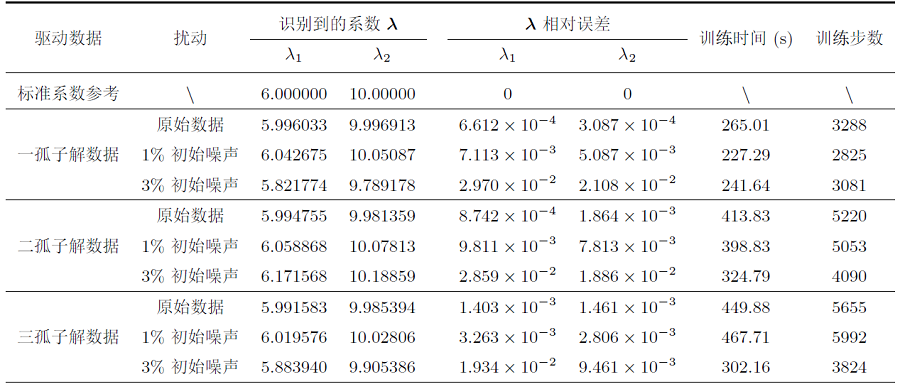
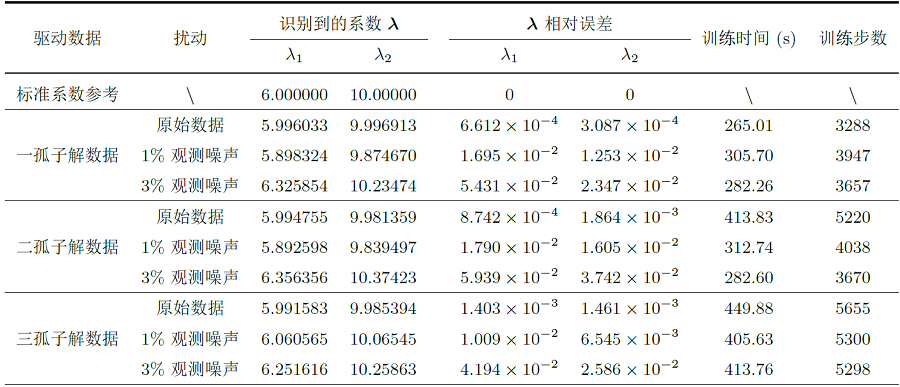
表 4 中“原始数据”一栏展示了分别由方程一、二、三孤子解数据驱动求解方程 (4.1) 系数的实验结果. 基于一孤子解 (11) 数据模拟待定系数时, 模型迭代 3288 次达到最优, 训练时长为 265.01 秒, 此时方程系数的预测值 $\lambda_1=5.996033$, $\lambda_2=9.996913$, 两者的相对误差均为 $\mathcal{O}(10^{-4})$; 基于二孤子解 (12) 数据模拟待定系数时, 模型迭代 5220 次达到最优, 训练时长为 413.83 秒, 此时方程系数的预测值 $\lambda_1=5.994755$, $\lambda_2=9.981359$, 其中 $\lambda_1$ 的相对误差为 $\mathcal{O}(10^{-4})$, 而 $\lambda_2$ 的相对误差为 $\mathcal{O}(10^{-3})$; 基于三孤子解 (13) 数据模拟待定系数时, 神经网络在训练 5655 步时达到最优, 训练时长为 449.88 秒, 此时方程系数的预测值 $\lambda_1=5.991583$, $\lambda_2=9.985394$, 其中 $\lambda_1$ 与 $\lambda_2$ 的相对误差均为 $\mathcal{O}(10^{-3})$.
4.2 噪声扰动对 PINNs 算法的影响
在偏微分方程数值求解时, 任何一个小的扰动都会带来解的急剧变化. 为了检验 PINNs 算法求解五阶 emKdV 方程的鲁棒性, 我们分别在初始条件和观测数据中添加高斯噪声 (概率密度函数服从正态分布的一类噪声), 即
(4.2) $ u_{\mathcal I}^{\delta}(x,t_{0})=\mathcal I(x,t_{0})+\varepsilon(x,t_{0}),$
(4.3) $ u_{\Omega}^{\delta}(x,t^{\prime})=u_{\Omega}(x,t^{\prime})+\varepsilon(x,t^{\prime}),$
其中 $\varepsilon(x,t)$ 为高斯噪声.
当分别在初始数据中加入 1%、 3% 的噪声时模型的预测情况如表 4 所示. 表格第二行给出了五阶 emKdV 方程的标准系数, 其中 $\lambda_1=6$, $\lambda_2=10$. 当在孤子解数据中加入 1% 的初始噪声时, 预测系数的相对误差依然可以达到 $\mathcal{O}(10^{-3})$; 当加入 3% 的初始噪声时, 预测系数的相对误差升高到了 $\mathcal{O}(10^{-2})$.
图 8(a) 、图 8(e) 和图 8(i) 所展示的预测解图像几乎相同, 加入 3% 的初始噪声并不会影响解的大致轮廓; 图 8 左侧第一列和第二列六幅图中的白色虚线标记出了 $t=1$ 时刻, 从误差动态图 8(b) 、 图 8(f) 和图 8(j) 中可以看出: 在 $t=1$ 时刻附近的误差要明显小于其它时刻, 因此我们也可以将 $t=1$ 处的已知信息理解为对模型的一次“校正”; 第三列和最后一列分别为 $t=-3$ 和 $t=4$ 时刻下精确解与预测解的比较, 这两个时刻对应图 7 前两列白色实线部分. 图 9 和图 10 分别展示了由二、三孤子解数据驱动下的结果. 不同颜色曲线的拟合程度反映了预测解与精确解的近似程度, 又因为此时的预测解对应了求得的预测系数, 所以曲线的近似程度也间接反映了预测系数的精度. 从误差动态图 10(j) 观察到: 当在方程的三孤子解数据加入 3% 的初始噪声, $t=-1$ 和 $t=6$ 时刻附近精确解与预测解之间的误差是比较大的, 但在图 10(k) 和图 10(l) 中可以看出, 此时基于预测系数的预测解 (蓝色虚线) 和精确解 (红色实线) 拟合效果依然非常好.
图 8
图 8
不同噪声下识别到的 emKdV 方程的一孤子解.
图 9
图 9
不同噪声下识别到的 emKdV 方程的二孤子解.
图 10
图 10
不同噪声下识别到的 emKdV 方程的三孤子解
表 5 展示了分别基于方程一、二、三孤子解实验数据并伴随 1%、 3% 的观测噪声时, 数据驱动识别待求系数的实验结果. 当在孤子解数据中加入 3% 的观测噪声时, 预测系数的相对误差依然可以达到 $\mathcal{O}(10^{-2})$; 与表 4 实验结果相比, 观测噪声对 PINNs 模型的影响要略大于初始噪声; 从表 4 和 表 5 中的实验数据不难看出, 基于多重孤子解数据驱动求解方程系数的 PINNs 模型具有很好的鲁棒性.
5 总结与展望
本文介绍了物理信息神经网络 (PINNs) 求解偏微分方程正反问题的主要步骤, 并验证双曲正切函数 $\tanh$ 作为激活函数求解五阶 emKdV 方程孤子解的有效性, 使用 $\tanh$ 作为激活函数求解一孤子解的精度可以达到 $\mathcal{O}(10^{-4})$, 二孤子解和三孤子解的精度可以达到 $\mathcal{O}(10^{-3})$. PINNs 深度学习方法在求解五阶 emKdV 方程反问题时具有很好的稳定性和鲁棒性, 当分别在孤子解的初始数据和观测数据中加入 3% 的高斯噪声, 预测系数的相对误差仍然可以达到 $\mathcal{O}(10^{-2})$. 数值实验显示 PINNs 方法不仅可以有效求解五阶 emKdV 方程的正反问题, 而且有助于发现和揭示孤子的动力学行为.
尽管目前有非常多的数值实验证实 PINNs 在数值求解非线性偏微分方程方面具有其独特的优势, 然而面对复杂的非线性问题, PINNs 在理论层面的分析尚有大量的工作需要完成, 包括损失函数的收敛问题和解的逼近问题.
参考文献
View Option
[1]
Draper L Freak wave Mar Obs , 1965 , 35 2 ): 193 -195
[本文引用: 1]
[3]
Zabusky N J Kruskal M D Interaction of "solitons" in a collisionless plasma and the recurrence of initial states
Phys Rev Lett , 1965 , 15 6 ): 240 -243
DOI:10.1103/PhysRevLett.15.240
URL
[本文引用: 1]
[6]
黄念宁 . 孤子理论和微扰方法 . 上海 : 上海科技教育出版社 , 1996
[本文引用: 1]
Huang N N Theory of Solitons and Method of Pertubations . Shanghai : Shanghai Scientific and Technological Education Press , 1996
[本文引用: 1]
[7]
Leblond H Grelu P Mihalache D Models for supercontinuum generation beyond the slowly-varying-envelope approximation
Phys Rev A , 2014 , 90 5 ): 053816
DOI:10.1103/PhysRevA.90.053816
URL
[本文引用: 1]
[8]
Ono H Soliton fission in anharmonic lattices with reflectionless inhomogeneity
J Phys Soc Jpn , 1992 , 61 12 ): 4336 -4343
DOI:10.1143/JPSJ.61.4336
URL
[本文引用: 1]
[9]
Khater A H El-Kalaawy O H Callebaut D K Bäcklund transformations and exact solutions for Alfvén solitons in a relativistic electron-positron plasma
Phys Scr , 1998 , 58 6 ): 545
DOI:10.1088/0031-8949/58/6/001
URL
[本文引用: 1]
[10]
Ito M An extension of nonlinear evolution equations of the KdV (mKdV) type to higher orders
J Phys Soc Jpn , 1980 , 49 2 ): 771 -778
DOI:10.1143/JPSJ.49.771
URL
[本文引用: 1]
[12]
Marchant T R Smyth N F The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography
J Fluid Mech , 1990 , 221: 263-287
[本文引用: 1]
[13]
Wazwaz A M Xu G Q An extended modified KdV equation and its Painlevé integrability
Nonlinear Dyn , 2016 , 86: 1455-1460
[本文引用: 3]
[14]
GrimShaw R PelinovSky E Poloukhina O Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface
Nonlin Processes Geophys , 2002 , 9 3/4 ): 221 -235
DOI:10.5194/npg-9-221-2002
URL
[本文引用: 1]
. A higher-order extension of the familiar Korteweg-de Vries equation is derived for internal solitary waves in a density- and current-stratified shear flow with a free surface. All coefficients of this extended Korteweg-de Vries equation are expressed in terms of integrals of the modal function for the linear long-wave theory. An illustrative example of a two-layer shear flow is considered, for which we discuss the parameter dependence of the coefficients in the extended Korteweg-de Vries equation.\n
[15]
Pelinovskii E N Polukhina O E Lamb K Nonlinear internal waves in the ocean stratified in density and current
Oceanology , 2000 , 40 6 ): 757 -766
[本文引用: 1]
[16]
Wang X Zhang J L Wang L Conservation laws, periodic and rational solutions for an extended modified Korteweg-de Vries equation
Nonlinear Dyn , 2018 , 92: 1507-1516
[本文引用: 1]
[17]
Liu N Guo B L Wang D S et al. Long-time asymptotic behavior for an extended modified Korteweg-de Vries equation
Commun Math Sci , 2019 , 17 7 ): 1877 -1913
DOI:10.4310/CMS.2019.v17.n7.a6
URL
[本文引用: 1]
[18]
Baydin A G Pearlmutter B A Radul A A et al. Automatic differentiation in machine learning: a survey
J March Learn Res , 2018 , 18: 1-43
[本文引用: 1]
[19]
Raissi M Perdikaris P Karniadakis G E Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
J Comput Phys , 2019 , 378: 686-707
[本文引用: 1]
[20]
Li J Chen Y Solving second-order nonlinear evolution partial differential equations using deep learning
Commun Theor Phys , 2020 , 72 10 ): 105005
DOI:10.1088/1572-9494/aba243
URL
[本文引用: 1]
[21]
Li J Chen Y A deep learning method for solving third-order nonlinear evolution equations
Commun Theor Phys , 2020 , 72 11 ): 115003
DOI:10.1088/1572-9494/abb7c8
[本文引用: 1]
<p>It has still been difficult to solve nonlinear evolution equations analytically. In this paper, we present a deep learning method for recovering the intrinsic nonlinear dynamics from spatiotemporal data directly. Specifically, the model uses a deep neural network constrained with given governing equations to try to learn all optimal parameters. In particular, numerical experiments on several third-order nonlinear evolution equations, including the Korteweg–de Vries (KdV) equation, modified KdV equation, KdV–Burgers equation and Sharma–Tasso–Olver equation, demonstrate that the presented method is able to uncover the solitons and their interaction behaviors fairly well.</p>
[22]
Li J H Chen J C Li B Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation
Nonlinear Dyn , 2022 , 107: 781-792
[本文引用: 1]
[24]
Wang L Yan Z Y Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schrödinger equation with a potential using the PINN deep learning
Phys Lett A , 2021 , 404: 127408
DOI:10.1016/j.physleta.2021.127408
URL
[本文引用: 1]
[25]
Cui S K Wang Z Han J Q et al. A deep learning method for solving high-order nonlinear soliton equations
Commun Theor Phys , 2022 , 74 7 ): 075007
DOI:10.1088/1572-9494/ac7202
[本文引用: 1]
We propose an effective scheme of the deep learning method for high-order nonlinear soliton equations and explore the influence of activation functions on the calculation results for higher-order nonlinear soliton equations. The physics-informed neural networks approximate the solution of the equation under the conditions of differential operator, initial condition and boundary condition. We apply this method to high-order nonlinear soliton equations, and verify its efficiency by solving the fourth-order Boussinesq equation and the fifth-order Korteweg–de Vries equation. The results show that the deep learning method can be used to solve high-order nonlinear soliton equations and reveal the interaction between solitons.
[26]
Li J H Li B Mix-training physics-informed neural networks for the rogue waves of nonlinear Schrödinger equation
Chaos, Solitons & Fractals , 2022 , 164: 112712
DOI:10.1016/j.chaos.2022.112712
URL
[本文引用: 1]
[27]
Jin P Z Lu L Tang Y F et al. Quantifying the generalization error in deep learning in terms of data distribution and neural network smoothness
Neural Networks , 2020 , 130: 85-99
[本文引用: 1]
[28]
Lu L Meng X H Mao Z P et al. DeepXDE: A deep learning library for solving differential equations
SIAM Rev , 2021 , 63: 208-228
[本文引用: 1]
[30]
Son H Jang J W Han W J et al. Sobolev training for physics informed neural networks . arXiv proprint arXiv: 2101. 08932.2021
[本文引用: 1]
[31]
Liu D C Nocedal J On the limited memory BFGS method for large scale optimization
Math Program , 1989 , 45 1 ): 503 -528
DOI:10.1007/BF01589116
URL
[本文引用: 1]
[33]
Jiao Y L Lai Y M Li D W et al. A rate of convergence of physics informed neural networks for the linear second order elliptic pdes
Commun Comput Phys , 2022 , 31 4 ): 1272 -1295
DOI:10.4208/cicp
URL
[本文引用: 1]
1
1965
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
Solitons in optical communications
1
1996
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
Interaction of "solitons" in a collisionless plasma and the recurrence of initial states
1
1965
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
The physics of trapped dilute-gas Bose-Einstein condensates
1
1998
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
The modified Korteweg-de Vries equation
1
1973
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
1
1996
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
1
1996
... 随着科学技术的发展, 线性模型已不足以反映客观世界的变化规律. 近几十年来, 流体力学、光纤通信、等离子体物理、生物学等领域中的非线性问题[1 ],[2 ],[3 ],[4 ] 越发受到人们的关注. 想要理解这些非线性现象的本质, 便要建立并求解这些非线性模型的偏微分方程 (PDE). 修正的 KdV (modified KdV, mKdV) 方程作为一类具有 $N$ 孤子解的完全可积方程[5 ],[6 ] , 其标准形式如下 ...
Models for supercontinuum generation beyond the slowly-varying-envelope approximation
1
2014
... 其中 $\sigma=\pm1$, $u=u(x,t)$ 是关于空间变量 $x$ 和时间变量 $t$ 的实函数. 方程 (1.1) 在众多的物理情形下具有重要应用, 例如: 光纤中超连续谱的产生[7 ] 、 晶格中孤子的传播[8 ] 、等离子体中非线性 Alfvén 波的传播[9 ] . 当考虑高阶色散时, 可以得到阶数更高的方程[10 ] . 经典的五阶 mKdV 方程具有如下形式 ...
Soliton fission in anharmonic lattices with reflectionless inhomogeneity
1
1992
... 其中 $\sigma=\pm1$, $u=u(x,t)$ 是关于空间变量 $x$ 和时间变量 $t$ 的实函数. 方程 (1.1) 在众多的物理情形下具有重要应用, 例如: 光纤中超连续谱的产生[7 ] 、 晶格中孤子的传播[8 ] 、等离子体中非线性 Alfvén 波的传播[9 ] . 当考虑高阶色散时, 可以得到阶数更高的方程[10 ] . 经典的五阶 mKdV 方程具有如下形式 ...
B?cklund transformations and exact solutions for Alfvén solitons in a relativistic electron-positron plasma
1
1998
... 其中 $\sigma=\pm1$, $u=u(x,t)$ 是关于空间变量 $x$ 和时间变量 $t$ 的实函数. 方程 (1.1) 在众多的物理情形下具有重要应用, 例如: 光纤中超连续谱的产生[7 ] 、 晶格中孤子的传播[8 ] 、等离子体中非线性 Alfvén 波的传播[9 ] . 当考虑高阶色散时, 可以得到阶数更高的方程[10 ] . 经典的五阶 mKdV 方程具有如下形式 ...
An extension of nonlinear evolution equations of the KdV (mKdV) type to higher orders
1
1980
... 其中 $\sigma=\pm1$, $u=u(x,t)$ 是关于空间变量 $x$ 和时间变量 $t$ 的实函数. 方程 (1.1) 在众多的物理情形下具有重要应用, 例如: 光纤中超连续谱的产生[7 ] 、 晶格中孤子的传播[8 ] 、等离子体中非线性 Alfvén 波的传播[9 ] . 当考虑高阶色散时, 可以得到阶数更高的方程[10 ] . 经典的五阶 mKdV 方程具有如下形式 ...
Soliton interaction for the extended Korteweg-de Vries equation
1
1996
... 从方程 (1.2) 及其拉格朗日量出发, 可以导出聚焦形式下包含非线性项 $u^{2}u_{xx}$ 和三阶色散项 $u_{xxx}$ 的扩展的五阶 mKdV (extended mKdV, emKdV) 方程[11 ],[12 ],[13 ] , 即 ...
The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography
1
1990
... 从方程 (1.2) 及其拉格朗日量出发, 可以导出聚焦形式下包含非线性项 $u^{2}u_{xx}$ 和三阶色散项 $u_{xxx}$ 的扩展的五阶 mKdV (extended mKdV, emKdV) 方程[11 ],[12 ],[13 ] , 即 ...
An extended modified KdV equation and its Painlevé integrability
3
2016
... 从方程 (1.2) 及其拉格朗日量出发, 可以导出聚焦形式下包含非线性项 $u^{2}u_{xx}$ 和三阶色散项 $u_{xxx}$ 的扩展的五阶 mKdV (extended mKdV, emKdV) 方程[11 ],[12 ],[13 ] , 即 ...
... 其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题. ...
... 对照文献 [13 ] 的步骤, 可得方程 (3.3) 一孤子解的表达式为 ...
Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface
1
2002
... 其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题. ...
Nonlinear internal waves in the ocean stratified in density and current
1
2000
... 其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题. ...
Conservation laws, periodic and rational solutions for an extended modified Korteweg-de Vries equation
1
2018
... 其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题. ...
Long-time asymptotic behavior for an extended modified Korteweg-de Vries equation
1
2019
... 其中 $0<\alpha<1$ 和 $0<\beta<1$ 分别代表相关非线性项的三阶和五阶色散系数. 方程 (1.3) 对于描述按密度和电流分层的流体中的非线性内波有一定的应用[14 ],[15 ] . 目前, 对于方程 (1.3) 解的研究已经有比较多的工作: 文献 [16 ] 导出了方程的无穷守恒律, 并通过达布变换方法求得了方程的周期解和有理解; 文献 [13 ] 使用简化的 Hirota 方法求解了方程 (1.3) 的孤子解, 并对其 Painlevé 可积性进行了讨论; 文献 [17 ] 借助非线性最速下降法分析了方程 (1.3) 解的长时间渐近行为. 本文主要研究聚焦形式下五阶 emKdV 方程 (1.3) 的正反问题. ...
Automatic differentiation in machine learning: a survey
1
2018
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
1
2019
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Solving second-order nonlinear evolution partial differential equations using deep learning
1
2020
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
A deep learning method for solving third-order nonlinear evolution equations
1
2020
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation
1
2022
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
梯度优化物理信息神经网络 (GOPINNs): 求解复杂非线性问题的深度学习方法
1
2023
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
梯度优化物理信息神经网络 (GOPINNs): 求解复杂非线性问题的深度学习方法
1
2023
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schr?dinger equation with a potential using the PINN deep learning
1
2021
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
A deep learning method for solving high-order nonlinear soliton equations
1
2022
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Mix-training physics-informed neural networks for the rogue waves of nonlinear Schr?dinger equation
1
2022
... 近几年, 随着人工智能的兴起, 科学家发现利用深度学习方法求解非线性问题具有其独特的优势: 例如在求解复杂区域上的 PDE 时, 只需在区域内随机取点, 使用自动微分计算导数[18 ] , 而不需要划分网格; 使用深度学习方法求解反问题要比传统方法简单的多, 而且可以在较高的精度下处理带有噪声的数据. 将深度学习方法与科学计算结合已经成为当下非常重要的课题, 其中具有代表性的工作便是 2017 年 Raissi, Perdikaris 和 Karniadakis 提出的物理信息神经网络 (PINNs), 其主要思想是将一些潜在的物理规律嵌入到神经网络方法当中, 便于直接从时空数据中揭示方程的动力学行为[19 ] . 与传统的神经网络相比, 该网络仅用非常少的数据便可获得相当精确的解, 充分体现了其在求解 PDE 正反问题中的优势. 2020 年, Li 和 Chen[20 ],[21 ] 基于 PINNs 深度学习方法, 在不同初始条件下, 对二阶 Burgers 方程和三阶 KdV 方程、mKdV 方程、STO 方程进行了数值求解, 并对方程孤子解的动力学行为进行了分析. 2021 年, Li 等[22 ],[23 ] 提出了梯度优化物理信息神经网络 (GOPINNs), 与原始的 PINNs 相比, GOPINNs 在求解某些复杂非线性问题时非常高效. Wang 和 Yan[24 ] 利用 PINNs 方法求解了散焦非线性薛定谔方程的怪波解, 并对其反问题做了研究. 2022 年, Cui 等[25 ] 借助 PINNs 方法对四阶 Boussinesq 方程及五阶 KdV 方程的孤子解进行了研究. Li[26 ] 基于先验信息, 提出了混合训练的物理信息神经网络 (MTPINNs), 数值结果表明改进后的模型不仅能快速模拟非线性薛定谔方程怪波解的动力学行为, 而且其逼近能力和绝对误差精度较原始 PINNs 也有明显提升. ...
Quantifying the generalization error in deep learning in terms of data distribution and neural network smoothness
1
2020
... 目前针对 PINNs 算法的研究不仅在经验上取得了成功, 在理论分析上也有显著成果. Jin 等[27 ] 从数据分布和神经网络光滑性的角度研究了分类问题中神经网络的泛化误差; Lu 等[28 ] 从宏观角度对 PINNs 的近似理论及误差来源做了简要分析; Wang 等[29 ] 则从神经正切核的角度分析了 PINNs 的训练动态, 并证明了全连接神经网络损失函数不同分量的收敛速度存在差异; Son 等[30 ] 提出了收敛速度更快的 Sobolev-PINNs, 并从理论上证明了改进后的损失函数可以保证神经网络在相应的 Sobolev 空间中收敛到方程的解. ...
DeepXDE: A deep learning library for solving differential equations
1
2021
... 目前针对 PINNs 算法的研究不仅在经验上取得了成功, 在理论分析上也有显著成果. Jin 等[27 ] 从数据分布和神经网络光滑性的角度研究了分类问题中神经网络的泛化误差; Lu 等[28 ] 从宏观角度对 PINNs 的近似理论及误差来源做了简要分析; Wang 等[29 ] 则从神经正切核的角度分析了 PINNs 的训练动态, 并证明了全连接神经网络损失函数不同分量的收敛速度存在差异; Son 等[30 ] 提出了收敛速度更快的 Sobolev-PINNs, 并从理论上证明了改进后的损失函数可以保证神经网络在相应的 Sobolev 空间中收敛到方程的解. ...
When and why PINNs fail to train: A neural tangent kernel perspective
1
2022
... 目前针对 PINNs 算法的研究不仅在经验上取得了成功, 在理论分析上也有显著成果. Jin 等[27 ] 从数据分布和神经网络光滑性的角度研究了分类问题中神经网络的泛化误差; Lu 等[28 ] 从宏观角度对 PINNs 的近似理论及误差来源做了简要分析; Wang 等[29 ] 则从神经正切核的角度分析了 PINNs 的训练动态, 并证明了全连接神经网络损失函数不同分量的收敛速度存在差异; Son 等[30 ] 提出了收敛速度更快的 Sobolev-PINNs, 并从理论上证明了改进后的损失函数可以保证神经网络在相应的 Sobolev 空间中收敛到方程的解. ...
1
08932.2021
... 目前针对 PINNs 算法的研究不仅在经验上取得了成功, 在理论分析上也有显著成果. Jin 等[27 ] 从数据分布和神经网络光滑性的角度研究了分类问题中神经网络的泛化误差; Lu 等[28 ] 从宏观角度对 PINNs 的近似理论及误差来源做了简要分析; Wang 等[29 ] 则从神经正切核的角度分析了 PINNs 的训练动态, 并证明了全连接神经网络损失函数不同分量的收敛速度存在差异; Son 等[30 ] 提出了收敛速度更快的 Sobolev-PINNs, 并从理论上证明了改进后的损失函数可以保证神经网络在相应的 Sobolev 空间中收敛到方程的解. ...
On the limited memory BFGS method for large scale optimization
1
1989
... 机器学习中解决优化问题常用的算法主要有牛顿法、梯度下降法、Adam 和 L-BFGS 优化算法. 本文主要使用 L-BFGS (Limited-memory BFGS) 优化器来对损失函数进行优化. L-BFGS 算法[31 ] 是一种基于二阶梯度来寻找目标函数最优值的拟牛顿优化算法, 其基本思想是只保存迭代过程中近 $m$ 次的迭代信息, 从而减少数据存储空间, 提升计算效率. 下面我们以一般的优化问题为例, 介绍牛顿法、BFGS 算法和 L-BFGS 算法的联系与区别. 假设多元函数优化问题的目标为 $\arg \min \limits_{\mathbf{x}} f(\mathbf{x})$, $\mathbf{x} \in \mathbb{R}^{n}$, 牛顿法利用函数 $f(\mathbf{x})$ 的前两项泰勒展开式来寻找方程 $f(\mathbf{x})=0$ 的根, 优点是收敛速度较快, 是一种二阶收敛的算法, 缺点是使用牛顿法需要消耗大量资源计算 Hessian 矩阵的逆 $H^{-1}$; BFGS 算法由牛顿法发展而来, 在继承了牛顿法二阶收敛的同时, 通过迭代计算 Hessian 矩阵的近似逆 $D^{-1}$, 进一步降低了运算成本; L-BFGS 算法可以看作 BFGS 算法的近似, 前者只存储和利用向量序列的部分信息 $\lbrace(\mathbf{x}_{i},\nabla f(\mathbf{x}_{i}))\rbrace_{i=1}^{m}$ 来减少内存花销. 图 2 对比展示了牛顿法、BFGS 算法与 L-BFGS 算法间的关系. ...
Large sample properties of simulations using Latin hypercube sampling
1
1987
... 对 (3.7) 式在区域 $x\in[-15,15]$, $t\in[-5,5]$ 内进行离散, 获得 512*201 个点的测试数据集. 借助拉丁超立方体抽样方法[32 ] 从上述数据集中抽取 $N_{\mathcal R}=10000$ 个内部配置点用于方程残差的训练; 选取 $N_{\mathcal I}=100$ 和 $N_{\mathcal B}=120$ 个点分别用于初始和边界条件的训练. ...
A rate of convergence of physics informed neural networks for the linear second order elliptic pdes
1
2022
... 表 1 比较了 ReLU、sigmoid、$\tanh$、$\sin$ 和 $\cos$ 函数 (五种激活函数在区间 [$-\pi,\pi$] 内的函数图像如图 3 所示) 对五阶 emKdV 方程一孤子解进行求解时的预测精度、运行时间和迭代步数, 结果表明: ReLU 激活函数对于当前问题的求解是失效的 (文献 [33 ] 在理论上解释了 ReLU 作为激活函数的神经网络没有办法在 $H^{2}(\Omega)$ 范数下逼近函数); 使用 sigmoid 作为激活函数时, 误差能在非常短的时间达到 $\mathcal{O}(10^{-3})$; 在当前数据集下, 选用双曲正切函数 $\tanh$ 和三角函数 $\sin$、$\cos$ 作为激活函数, 均可使最后的 $L^2$ 相对误差达到 $\mathcal{O}(10^{-4})$, 但是 $\tanh$ 所消耗的时间和训练步数均小于三角函数, 所以本文选用 $\tanh$ 作为激活函数求解 emKdV 方程的一孤子解. ...
