1 引言
(1.1) $ \begin{cases}\partial_tu + \partial_x(uv)=0,\\\partial_t v-\partial_xu=0,\end{cases}$
$t>0$, $x\in \mathbb{R}$.
(1.2) $ \begin{cases} \partial_tp=D\partial_x(p\partial_x\ln(\frac{p}{\Phi(\omega)})),\\ \partial_t\omega=(\lambda p-\mu)\omega+\varepsilon\partial_x^2\omega,\end{cases}$
其中 $p(x,t)$ 表示粒子密度, $\omega(x,t)$ 表示物质的浓度, $D$ 表示粒子的扩散率. 函数 $\Phi$ 通常被称为趋化势能, 其公式为
(1.3) $ \Phi(\omega)=\omega^{-\alpha}.$
如果 $\alpha<0$, 则称为正趋化, 反之, 则称为负趋化. 利用 (1.3) 式, 通过变换
(1.4) $ u=p,v=\partial_x(\ln\omega).$
(1.5) $ \begin{cases}\partial_tu-\alpha D \partial_x(uv)=D\partial_x^2u,\\\partial_t v-\partial_x(\lambda u+\varepsilon v^2)=\varepsilon\partial_x^2v.\end{cases}$
(1.6) $ \tilde{t}=\lambda t, \tilde{x}=\sqrt{\frac{\lambda}{-\alpha D}}x,\tilde{v}=\sqrt{\frac{-\alpha D}{\lambda}}v, \tilde{\varepsilon}=\frac{\varepsilon}{-\alpha D}, \tilde{D}=-\frac{1}{\alpha}.$
为了简单起见, 令 $\tilde{t}=t, \tilde{x}=x, \tilde{v}=v, \tilde{\varepsilon}=\varepsilon, \tilde{D}=D$, (1.5) 式简化为
(1.7) $ \begin{cases}\partial_tu + \partial_x(uv)=D\partial_x^2u,\\\partial_t v-\partial_x( u+\varepsilon v^2)=\varepsilon\partial_x^2v.\end{cases}$
(1.1) 式是 (1.7) 式的一个特例 ($D=0$, $\varepsilon=0$), 也是混合型. 通过计算, 若 $v^2\geq4u$, 方程 (1.1)是双曲型; 若 $v^2<4u$, 方程 (1.1) 是椭圆型; 若 $v^2=4u$, 方程 (1.1) 是非严格双曲型. 此外, 如果 $u=0, v>0$, 第一特征族是线性退化的. 如果 $u=0, v<0$, 第二特征族是线性退化的.
近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ].
本文考虑方程 (1.1) 的黎曼问题, 黎曼初值满足
(1.8) $ U_0=(v,u)|_{t=0}=\begin{cases}U_-=(v_-,u_-) \quad x<0,\\U_+=(v_+,u_+) \quad x>0.\end{cases}$
在第 2 节中, 我们介绍了方程 (1.1) 的一些基本性质以及基本波情况. 在第 3 节中, 关于 $u\geq0$, 我们构造了左右状态在同一象限以及不同象限的黎曼解. 特别地, 当左状态在第二象限, 右状态在第一象限时, 该初值问题都是黎曼可解的.
2 预备知识
本节主要是介绍方程 (1.1) 的一些基本性质与基本波情况. 在光滑解意义下, 方程 (1.1) 可以等价为
(2.1) $ \lambda_1=\frac{v-\sqrt{v^2-4u}}{2},\quad \lambda_2=\frac{v+\sqrt{v^2-4u}}{2},$
易知, 若 $v^2\geq4u$, 方程 (1.1) 是双曲型. 若 $v^2<4u$, 方程 (1.1) 是椭圆型. 经计算
(2.2) $ \nabla \lambda_1\cdot r_1=1-\frac{v}{\sqrt{v^2-4u}}, \quad \nabla \lambda_2\cdot r_2=1+\frac{v}{\sqrt{v^2-4u}},$
这意味着, 如果 $v^2-4u>0$ 且 $u\neq0$, 对于每一个特征值都是真正非线性的. 其相应的基本波只可能是激波或稀疏波. 如果 $u=0, v>0$, 第一特征族是线性退化的. 如果 $u=0, v<0$, 第二特征族是线性退化的. 其相应的基本波分别是 1-接触间断 $J_1$ 和 2-接触间断 $J_2$.
根据 $k$-Riemann 不变量[16 ] 的定义, 我们得到了 1-Riemann 不变量和 2-Riemann 不变量的表达式
(2.3) $ w_1=(\Omega-v)(\Omega+2v)^2,$
(2.4) $ w_2=(\Omega+v)(\Omega-2v)^2,$
其中 $\Omega=\sqrt{v^2-4u}$. 值得注意的是 $w_1(v,u)=w_2(-v,u)$. 此外
(2.5) $ \begin{cases}w_1=0, \qquad u=0 (v>0),\\w_2=0,\qquad u=0 (v<0).\end{cases}$
下面我们将介绍混合型方程组的激波. 设间断线为 $s=\frac{{\rm d}x}{{\rm d}t}$, 根据 Rankine-Hugoniot 条件[16 ] , 可得
(2.6) $ \begin{cases}s[u]=[uv], \\s[v]=-[u],\end{cases}$
其中 $[a]=a-a_-$. 消除 (2.6) 式中 $s$, 则有
(2.7) $ [u]^2+[v][uv]=0.$
(2.8) $ (u-u_-)^2+v(u-u_-)(v-v_-)+u_-(v-v_-)^2=0,$
(2.9) $ s(v;v_-,u_-)=-\frac{u-u_-}{v-v_-}=\frac{v\pm\sqrt{v^2-4u_-}}{2}, \quad v^2>4u_-.$
由于椭圆域的存在, Lax 熵条件[16 ] 不再适用. 利用 Hsiao 等[4 ] 所提的一般熵条件, 可知 1-激波曲线 $S_1(v;v_-,u_-)$ 满足
(2.10) $ S_1: \begin{cases}s_1(v;v_-,u_-)=\displaystyle\frac{v-\sqrt{v^2-4u_-}}{2},\\[3mm]u=u_-\displaystyle\frac{v-\sqrt{v^2-4u_-}}{2}(v-v_-), v<v_-.\end{cases}$
2-激波曲线 $S_2(v;v_-,u_-)$ 满足
(2.11) $ S_2: \begin{cases}s_2(v;v_-,u_-)=\displaystyle\frac{v+\sqrt{v^2-4u_-}}{2},\\[3mm]u=u_-\displaystyle\frac{v+\sqrt{v^2-4u_-}}{2}(v-v_-), v<v_-.\end{cases}$
接下来我们寻求 $(v,u)(x,t)=(u,v)(\xi)$, $\xi=\frac{x}{t}$ 形式的自相似解. 利用 (2.3) 式和 (2.4) 式, 我们推导出 1-稀疏波 $R_1$ 和 2-稀疏波 $R_2$ 如下
(2.12) $ R_1: \begin{cases}\sqrt{\Omega-v} (\Omega+2v)=\sqrt{\Omega_-v_-}(\Omega_-+2v_-), \quad & v<0,\\\sqrt{-\Omega+v} (\Omega+2v)=\sqrt{-\Omega_-+v_-}(\Omega_-+2v_-), \quad& v>0.\end{cases}$
(2.13) $ R_2: \begin{cases}\sqrt{\Omega+v} (\Omega-2v)=\sqrt{\Omega_-+v_-}(\Omega_-2v_-), \quad &v>0,\\\sqrt{-\Omega-v} (\Omega-2v)=\sqrt{-\Omega_-v_-}(\Omega_-2v_-), \quad& v<0,\end{cases}$
其中 $\Omega=\sqrt{v^2-4u}$, $\Omega_-=\sqrt{v_-^2-4u_-}$.
(2.14) $ \begin{aligned}u'(v)=\frac{\Omega-v}{2}\begin{cases} >0,\qquad v<0, \\ <0,\qquad {v>0, } \end{cases}\\u"(v)=\frac{v-\Omega}{\Omega} \begin{cases}<0,\qquad v<0, \\ >0,\qquad {v>0. } \end{cases}\end{aligned}$
由于稀疏波的特征速度随着 $\frac{x}{t}$ 的增加而增加, 这就意味着 $\lambda_1(v_-, u_-)<\lambda_1(v,u)$. 从
(2.15) $ \frac{\text{d}\lambda_1(v,u(v))}{{\rm d}v}=\frac{\Omega-v+2u'(v)}{2\Omega}=\frac{\Omega-v}{\Omega}\begin{cases} >0,\qquad v<0,\\<0,\qquad v>0, \end{cases}$
(2.16) $ R_1: \begin{cases} v>v_-,\qquad v<0, \\ v<v_-,\qquad v>0. \end{cases}$
类似地, 2-稀疏波 $R_2$ 的一阶导和二阶导为
(2.17) $ \begin{aligned}& u'(v)=-\frac{\Omega+v}{2} \begin{cases} <0,\qquad v>0, \\ >0,\qquad v<0, \end{cases}\\&u"(v)=-\frac{\Omega+v}{\Omega} \begin{cases}<0,\qquad v>0, \\ >0,\qquad v<0, \end{cases}\\&\frac{\text{d}\lambda_2(v,u(v))}{{\rm d}v}=\frac{\Omega+v-2u'(v)}{2\Omega}=\frac{\Omega+v}{\Omega}\begin{cases} >0,\qquad v>0, \\ <0,\qquad v<0. \end{cases}\end{aligned}$
(2.18) $ R_2: \begin{cases} v>v_-,\qquad v>0, \\ v<v_-,\qquad v<0. \end{cases}$
3 黎曼解
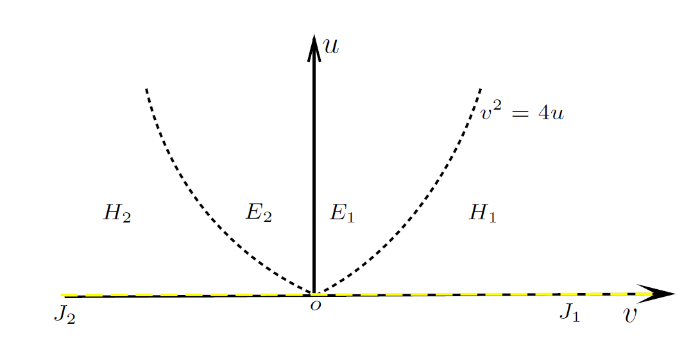
本节中, 我们构造了$u\geq0$ 方程 (1.1) (7) 的黎曼解. 首先, 我们将区域划分如下
其中 $H$ 满足 $v^2-4u\geq 0$, 是非严格双曲域, $E$ 满足 $v^2-4u< 0$, 是椭圆域. $H_{1}\cup E_{1}$ 是第一象限, $H_{2}\cup E_{2}$ 是第二象限.
图 1
记 $U_{-}=(v_{-},u_-)$, $U_{+}=(v_{+},u_+)$, $U_{m}=(v_{m},u_m)$. 接下来, 我们主要研究固定左状态 $U_{-}$ 在双曲域的情形, 当左状态在椭圆域的情况可参见文献 [5 ]. 关于方程 (1.1) (7) 的黎曼问题分两种情况讨论. 如果 $U_{-}$ 和 $U_{+}$ 都在同一象限, 主要结果如下.
定理 3.1 假设 $u\geq0$, $U_{m}$ 是连接 $U_{-}$ 和 $U_{+}$ 的中间状态. 方程 (1.1) (7) 在同一象限的黎曼解构造如下
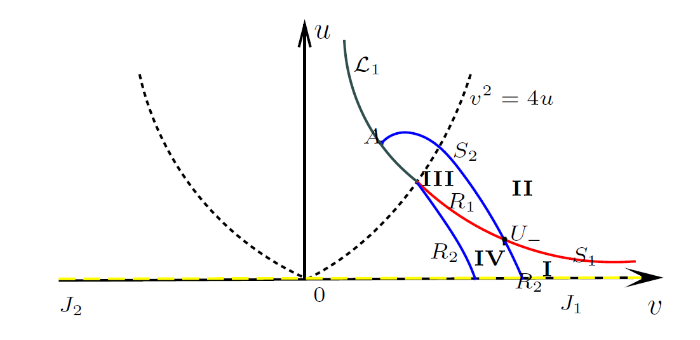
(a) $U_{-}$, $U_{+} \in H_1 $. (见图 2 )
图 2
如果 $(v_{+},u_+)\in I $, $(v_{-},u_-)\xrightarrow{S_1}(v_{m},u_m)\xrightarrow{R_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in II $, $(v_{-},u_-)\xrightarrow{S_1}(v_{m},u_m)\xrightarrow{S_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in III $, $(v_{-},u_-)\xrightarrow{R_1}(v_{m},u_m)\xrightarrow{S_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in IV $, $(v_{-},u_-)\xrightarrow{R_1}(v_{m},u_m)\xrightarrow{R_2}(v_{+},u_+)$.
其中$II$, $III$ 可解域即包含于 $E_1$ 区域也包含于 $H_1$ 区域.
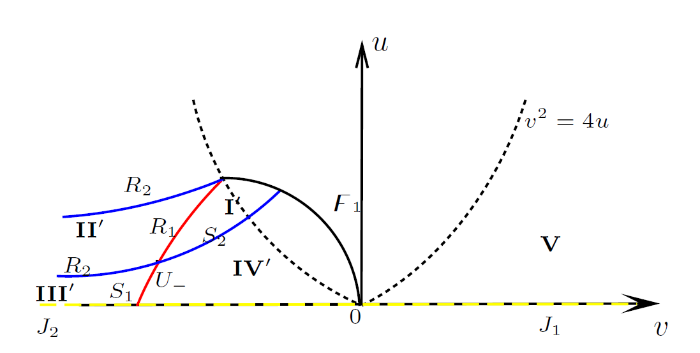
(b) $U_{-}$, $U_{+} \in H_2 $. (见图 3 )
图 3
如果 $(v_{+},u_+)\in I' $, $(v_{-},u_-)\xrightarrow{R_1}(v_{m},u_m)\xrightarrow{S_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in II' $, $(v_{-},u_-)\xrightarrow{R_1}(v_{m},u_m)\xrightarrow{R_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in III' $, $(v_{-},u_-)\xrightarrow{S_1}(v_{m},u_m)\xrightarrow{R_2}(v_{+},u_+)$,
如果 $(v_{+},u_+)\in IV' $, $(v_{-},u_-)\xrightarrow{S_1}(v_{m},u_m)\xrightarrow{S_2}(v_{+},u_+)$.
其中$I'$, $IV'$ 可解域即包含于 $E_2$ 区域也包含于 $H_2$ 区域.
注 3.1 曲线$\mathcal{L}_{1}$ 满足
(3.1) $ \begin{cases}u_m=u_-\displaystyle\frac{v_m-\sqrt{v_m^2-4u_-}}{2}(v_m-v_-),\\[3mm]u=u_m-\displaystyle\frac{v+\sqrt{v^2-4u_m}}{2}(v-v_m),\end{cases}$
其中 $v=-2\sqrt{u_m}$, $ 0\leq u_m \leq -\sqrt{u_{-}}(\sqrt{u_{-}}+v_-)$. 易知, 曲线 $\mathcal{L}_{2}$ 也由方程 (3.1) 表示, 其中 $v=2\sqrt{u_m}$, $v_m>\frac{4u_{-}+v^{2}_{-}}{2v_{-}}$.
如果 $U_{-}$ 和 $U_{+}$ 不在同一象限, 主要结果如下.
定理3.2 假设 $u\geq0$, $U_{m}$ 是连接 $U_{-}$ 和 $U_{+}$ 的中间状态. 若 $U_{-}$ 在第二象限, $U_{+}$ 在第一象限, 方程 (1.1), (7) 的黎曼解包含激波, 稀疏波和接触间断 (见图 3 , 图 4 ), 并且存在 2-接触间断跳跃到 1-接触间断的现象. 如果 $(v_{+},u_+)\in V$, 其黎曼解构造为
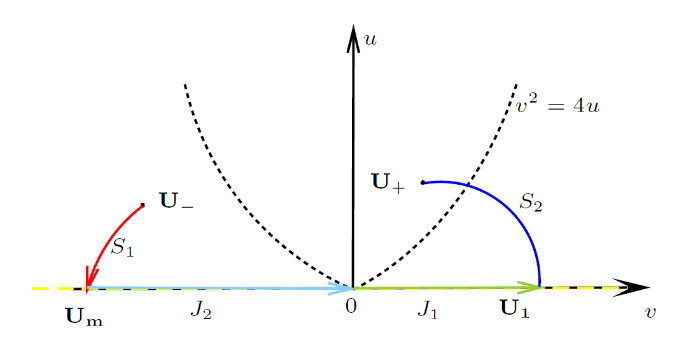
图 4
$v_{m}<0$, $(v_{1},0)$ 也是一个中间状态且满足 $v_{1}>0$. 特别地, 可解域 $V$ 是整个第一象限.
注 3.2 如果 $u_-=0, v_->0$, 激波曲线满足 $u=-({v}^2-vv_-)$, 它是关于$v=\frac{v_-}{2}$ 对称的, 且经过原点 $(0,0)$.
推论 3.1 若 $U_{-} $ 在第二象限, $U_{+}$ 在第一象限, 且 $U_{-}, U_{+}$ 均在 $v$ 轴上, 那么方程 (1.1), (7) 的黎曼解构造为
参考文献
View Option
[1]
Guo J Xiao J X Zhao H J et al. Global solutions to a hyperbolic-parabolic coupled system with large initial data
Acta Math Sci , 2009 , 29B 3 ): 629 -641
[本文引用: 1]
[2]
Horstmann D From 1970 until present: the Keller-Segel model in chemotaxis and its consequences
Jahresbericht der Deutschen Mathematiker-Vereinigung , 2003, 105: 103-165
[本文引用: 1]
[3]
Hou Q Q Wang Z A Zhao K Boundary layer problem on a hyperbolic system arising from chemotaxis
J Differential Equations , 2016 , 261: 5035-5070
[本文引用: 1]
[4]
Hsiao L De Mottoni P Existence and uniqueness of the Riemann problem for a nonlinear system of conservation laws of mixed type
Transactions of the American Mathematical Society , 1990 , 332 2 ): 121 -158
DOI:10.1090/tran/1992-332-01
URL
[本文引用: 2]
[5]
He F Wang Z Chen T T The shock waves for a mixed-type system from chemotaxis
Acta Math Sci , 2023 , 43B 4 ): 1717 -1734
[本文引用: 1]
[9]
Li H C Zhao K Initial-boundary value problems for a system of hyperbolic balance laws arising from chemotaxis
J Differential Equations , 2015 , 258: 302-338
[本文引用: 1]
[10]
Li T Pan R Zhao K Global dynamics of a hyperbolic-parabolic model arising from chemotaxis
SIAM J Appl Math , 2012 , 72: 417-443
[本文引用: 1]
[11]
Li J Wang L Zhang K Asymptotic stability of a composite wave of two traveling waves to a hyperbolic-parabolic system modeling chemotaxis
Math Methods Appl Sci , 2013 , 36: 1862 -1877
DOI:10.1002/mma.v36.14
URL
[本文引用: 1]
[12]
Li T Wang Z A Nonlinear stability of travelling waves to a hyperbolic-parabolic system modeling chemotaxis
SIAM J Appl Math , 2009 , 70: 1522-1541
[本文引用: 1]
[13]
Li T Liu H Wang L Oscillatory traveling wave solutions to an attractive chemotaxis system
J Differential Equation , 2016 , 261: 7080-7098
[本文引用: 2]
[14]
Li T Mathur N Rienmann problem for a non-strictly hyperbolic system in chemotaxis
Discrete and Continuous Dynamical System Series B , 2022 , 27 4 ): 2173 -2187
DOI:10.3934/dcdsb.2021128
URL
[本文引用: 2]
[15]
Li J Y Li T Wang Z A Stability of traveling waves of the Keller-Segel system with logarithmic sensitivity
Math Models Methods Appl Sci , 2014 , 24: 2819-2849
[本文引用: 1]
[16]
Smoller J Shock Waves and Reaction-Diffusion Equations . New York : Springer-Verlag , 1994
[本文引用: 3]
[17]
Zhang M Zhu C J Global existence of solutions to a hyperbolic-parabolic system
Proc Amer Math Soc , 2007 , 135 4 ): 1017 -1027
DOI:10.1090/S0002-9939-06-08773-9
URL
[本文引用: 1]
Global solutions to a hyperbolic-parabolic coupled system with large initial data
1
2009
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
From 1970 until present: the Keller-Segel model in chemotaxis and its consequences
1
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Boundary layer problem on a hyperbolic system arising from chemotaxis
1
2016
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Existence and uniqueness of the Riemann problem for a nonlinear system of conservation laws of mixed type
2
1990
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
... 由于椭圆域的存在, Lax 熵条件[16 ] 不再适用. 利用 Hsiao 等[4 ] 所提的一般熵条件, 可知 1-激波曲线 $S_1(v;v_-,u_-)$ 满足 ...
The shock waves for a mixed-type system from chemotaxis
1
2023
... 记 $U_{-}=(v_{-},u_-)$, $U_{+}=(v_{+},u_+)$, $U_{m}=(v_{m},u_m)$. 接下来, 我们主要研究固定左状态 $U_{-}$ 在双曲域的情形, 当左状态在椭圆域的情况可参见文献 [5 ]. 关于方程 (1.1) (7) 的黎曼问题分两种情况讨论. 如果 $U_{-}$ 和 $U_{+}$ 都在同一象限, 主要结果如下. ...
Model for chemotaxis
1
1971
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Traveling bands of chemotactic bacteria: a theoretical analysis
1
1971
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Initiation of slime mold aggregation viewed as an instability
1
1970
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Initial-boundary value problems for a system of hyperbolic balance laws arising from chemotaxis
1
2015
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Global dynamics of a hyperbolic-parabolic model arising from chemotaxis
1
2012
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Asymptotic stability of a composite wave of two traveling waves to a hyperbolic-parabolic system modeling chemotaxis
1
2013
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Nonlinear stability of travelling waves to a hyperbolic-parabolic system modeling chemotaxis
1
2009
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Oscillatory traveling wave solutions to an attractive chemotaxis system
2
2016
... 该方程 (1.1) 源于趋化模型[13 ] ...
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Rienmann problem for a non-strictly hyperbolic system in chemotaxis
2
2022
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
... 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
Stability of traveling waves of the Keller-Segel system with logarithmic sensitivity
1
2014
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
3
1994
... 根据 $k$-Riemann 不变量[16 ] 的定义, 我们得到了 1-Riemann 不变量和 2-Riemann 不变量的表达式 ...
... 下面我们将介绍混合型方程组的激波. 设间断线为 $s=\frac{{\rm d}x}{{\rm d}t}$, 根据 Rankine-Hugoniot 条件[16 ] , 可得 ...
... 由于椭圆域的存在, Lax 熵条件[16 ] 不再适用. 利用 Hsiao 等[4 ] 所提的一般熵条件, 可知 1-激波曲线 $S_1(v;v_-,u_-)$ 满足 ...
Global existence of solutions to a hyperbolic-parabolic system
1
2007
... 近些年来, 对于模型 (1.7) 中 $D>0$ 的情况, 研究成果比较完善. 2007 年, Zhang 和 Zhu[17 ] 证明了小初值下全局解的存在性. 2016 年, Li, Liu 和 Wang[13 ] 研究了 $D=1, \varepsilon>0$ 时的行波解. 对于方程 (1.1), Li 等[14 ] 解决了双曲域中同一区域的黎曼问题. 本文利用 Hsiao 等[4 ] 所提的一般熵条件, 扩展了文献 [14 ] 中的黎曼可解区域, 并刻画了左右状态在不同象限的黎曼解构造. 关于趋化模型的更多结果, 可以参考文献 [1 ],[2 ],[3 ],[6 ],[7 ],[8 ],[9 ],[10 ],[11 ],[12 ],[15 ]. ...
