迭代方程的研究不仅对函数方程理论的发展有重要作用^[1],[27], 而且在动力系统的研究中也有广泛的应用^[2],[8]. 例如, 著名的 Feigenbaum 方程^{[12],[19],[26]}

其中 $ \lambda\in \rm{(0, 1)} $ 是固定的常数, $ f: \rm{[0,1]}\rightarrow\rm{[0,1]} $ 是未知的函数, 可以用它来刻画环上的映射产生混沌的拟周期路径. 此外, 在平面映射的不变曲线研究中^{[11],[16],[17]}, 关键的一个步骤就是解下面的函数方程

其中 $ \phi $ 是已知的实连续函数. 事实上, 方程 (1.2) 与方程 (1.1) 在 $ \lambda=1 $ 时是下面的一般迭代方程的特殊情形

其中 $ X $ 是 $ \mathbb{R} $ 的一个非空子集, $ G,F: X\to X $ 都是已知函数, $ f^{n} $ 表示未知函数 $ f: X\to X $ 的 $ n $ 次迭代, 即: $ f^{n}(x):=f(f^{n-1}(x)) $ 并且 $ f^{0}(x):=x, x\in X $. 特别, 如果 $ G $ 是线性的, 方程 (1.3) 就是著名的多项式型迭代函数方程

其中 $ \alpha_{i}, i=1, 2,\cdot\cdot\cdot,n $, 都是实常数. 方程 (1.4) 与很多重要问题密切相关, 比如动力系统中的正规形理论^[2], 微分同胚同宿轨的横截相交性^[7], 平面映射的动力学性质^[8]以及不变曲线^[11], 这些问题都吸引了很多研究者去寻找它的解. 对于方程 (1.4) 中的 $ F $ 是线性的情况, 它的连续解在文献 [10],[23],[25] 中已经给出. 然而对于非线性情况, 由于迭代的非线性性，问题就变得非常复杂, 像解的存在性和唯一性这些基本问题都很难解决. 直到 1987 年, 张伟年^[28] 通过构造含有函数迭代的线性组合的结构算子, 在 $ \alpha_{1}>0 $ 不太大的条件下应用不动点定理得到了方程 (1.4) 解的存在性. 后来按照这个思路, 研究者们又得到像光滑解, 凸解, 对称解 ^{[15],[29],[31]}这些结论. 由于 $ \alpha_{1}>0 $ 这个强加的条件不自然, 为了克服这个条件, 不少研究者花费大量的精力去研究自然假设 $ \alpha_{m}>0 $ 下方程 (1.4) 解的存在性这个公开问题 (简称首项系数问题)^[27],[30]. 另一方面, 对于 $ F $ 在不动点是非双曲的扩张情形, 研究者利用 Schauder's 不动点定理得到方程 (1.4) 在不动点邻域的局部 $ C^{1} $ 解^[4]. 2007 年, 研究者^[24]采用不同于文献 [4] 中的方法构造出方程 (1.4) 在有一个端点是 $ F $ 的不动点的闭区间上无穷多个 $ C^{0} $ 递增解. 基于文献 [24] 的结论, 张文萌等人利用在区间的一个端点是局部线性解的序列来逼近真解的办法得到两个不动点之间的全局递增连续解^[32]. 之后, 李林和张文萌对 $ F $ 在原点某个邻域是线性的且方程 (1.4) 的阶数 $ n $ 为偶数的情形下, 给出它的 $ C^{0} $ 递减解^[14]. 关于利用特征分析的方法来得到方程 (1.4) 解的结论可以参考文献 [5],[6],[18],[20],[33].

值得注意的是迭代方程的同胚解在化简函数方程以及动力系统的线性化和共轭变换中起到重要作用^{[3],[21],[34],[35]}. 实际上, 已经有不少研究者在努力寻找这种解. 2013 年, 对于局部线性函数 $ F $, 研究者考虑方程 (1.4) 的阶数 $ n $ 为偶数时的递减同胚解^[14]. 随后, 宋威等人^[13],[22]对一般方程 (1.3) 在 $ F $ 是 $ C^1 $ 并且 $ F' $ 是 Lipschitzian 的条件下得到递增和递减的同胚解. 本文是文献 [13],[14],[22],[32] 这些工作的延续. 在本文中, 我们首先讨论除去文献 [13],[22] 中所要求的 Lipschitzian 条件下方程 (1.3) 的同胚解. 然后, 将所得到的主要结论应用到求解多项式型迭代方程 (1.4).

在本文中, 设 $ I:=[-1,1] $ 和 $ J:=[0,1] $ 为紧区间.

令 $ \vec{x}:=(x_{1}, x_{2},\cdot\cdot\cdot,x_{n})\in\mathbb{R}^{n} $, 其中 $ x_{1}, x_{2},\cdot\cdot\cdot,x_{n}\in\mathbb{R} $. 对于 $ a\neq b\in \mathbb{R} $ 和 $ n\in\mathbb{N} $, 记 $ \overrightarrow{(a, b)_{n}} $, 这里 $ (a, b, a, b,\cdot\cdot\cdot)\in\mathbb{R}^{n} $. 显然 $ a $ 位于奇数位置而 $ b $ 位于偶数位置. 例如, $ \overrightarrow{(1, 2)_{4}}=(1, 2, 1, 2) $ 和 $ \overrightarrow{(1, 2)_{5}}=(1, 2, 1, 2, 1) $. 令 $ C(L_{1},L_{2}):=\{f\in C(L_{1})| f(L_{1})\subset L_{2}\} $, 其中 $ L_{1} $ 和 $ L_{2} $ 都是紧区间并且 $ C(L_{1}) $ 是由定义在 $ L_{1} $ 上的所有连续函数所组成. 进一步, 令

称多元函数 $ G: \mathbb{R}^n \to \mathbb{R} $ 为齐次的, 如果它满足下面的条件

设 $ \vec{x} $, $ \vec{y}\in \mathbb{R}^{n} $. 如果对所有的 $ i=1, 2,\cdot\cdot\cdot, n $ 都有 $ x_{i}\geq y_{i} $, 则我们在$ \vec{x} $ 与 $ \vec{y} $ 之间定义一个偏序为 $ \vec{x}\succeq_{1} \vec{y} $. 如果对所有奇数 $ i $, $ x_{i}\geq y_{i} $ 且对于所有偶数 $ i $, 有 $ x_{i} \leq y_{i} $, 则 $ \vec{x} $ 与 $ \vec{y} $ 之间的偏序定义为 $ \vec{x}\succeq_{2} \vec{y} $. 用 $ \Lambda(L^{n},L) $ 表示从 $ L^{n} $ 到 $ L $ 所有连续齐次函数的集合, 其中 $ L $ 是一个紧区间, $ L^{n}:=\underbrace{L \times L\times L\cdot\cdot\cdot\times L}_{n \rm times} $.

定义

其中条件 ({C}$_{1}$)-({C}$_{3}) $ 定义如下

(C$_{1}$) : $ G $ 关于每个变量 $ x_{i} $, $ x_{i}\in J $, $ i=1,2,\cdots,n $, 是严格递增的.

(C$_{2}$) : 对于 $ \vec{x},\vec{y}\in J^{n} $ 且满足 $ \vec{x}\succeq_{1} \vec{y} $, 都有$ |G(\vec{x})-G(\vec{y})|\geq\|\vec{x}-\vec{y}\|_{*} $, 这里 $ \|\cdot\|_{*} $ 是 $ \mathbb{R}^{n} $ 上的一个范数, 定义为 $ \|\vec{z}\|_{*}:=\frac{1}{n}\sum\limits_{i=1}^{n}|z_{i}|, \vec{z}\in \mathbb{R}^{n} $.

(C$_{3}$) : $ G(0, 0,\cdot\cdot\cdot, 0)=0 $, $ G(1, 1,\cdot\cdot\cdot, 1)=1 $.

同时, 定义

其中条件 ({D}$_{1})$-({D}$_{3}) $ 定义如下

$ (\rm{D}_{1}) $: $ G $ 关于偶下标变量 $ x_{i} $ 是递增的而关于奇下标变量 $ x_{i} $ 是递减的, 这里 $ x_{i}\in I, $ $i=1,2,\cdots,n $.

$ (\rm{D}_{2}) $: 对于任意 $ \vec{x},\vec{y}\in I^{n} $ 满足 $ \vec{x}\succeq_{2} \vec{y} $ 有 $ |G(\vec{x})-G(\vec{y})|\geq\| \vec{x}-\vec{y}\|_{*} $.

$ (\rm{D}_{3}) $: $ G(0, 0,\cdot\cdot\cdot, 0)=0 $, $ G(\overrightarrow{(1, -1)_{n}})=-1 $, $ G(\overrightarrow{(-1, 1)_{n}})=1 $.

例2.1 设 $ G_1(x_{1},x_{2},x_{3})=\frac{1}{3}x_{1}+\frac{1}{3}x_{2}+\frac{1}{3}x_{3}, x_{1},x_{2},x_{3}\in J $. 显然 $ G_1 $ 是一个连续的齐次函数并且满足条件 ({C}$_{1})$-({C}$_{3}) $. 因此 $ G_1\in M(J^{3}) $.

设 $ G_2(x_{1},x_{2},x_{3})=-\frac{1}{3}x_{1}+\frac{1}{3}x_{2}-\frac{1}{3}x_{3}, x_{1},x_{2},x_{3}\in I $. 可以验证 $ G_2 $ 是一个连续的齐次函数并且满足条件 ({D}$_{1})$-({D}$_{3}) $. 因此 $ G_2\in N(I^{3}) $.

引理2.1^[引理1] 设 $ g, g_{m}\in C(\tilde{I}) $, $ f, f_{m}\in C(\tilde{I},\tilde{I}), m\in \mathbb{N} $ 并且满足当 $ m\rightarrow\infty $ 时, $ g_{m}\rightarrow g, f_{m}\rightarrow f $. 那么当 $ m\rightarrow \infty $ 时, $ g_{m}\circ f_{m}\rightarrow g\circ f $. 另外, 如果 $ f $ 和所有的 $ f_{m} $ ($ m\in \mathbb{N}) $ 都在集合 $ H(\tilde{I},\tilde{I}) $ 中, 则当 $ m\rightarrow\infty $ 时, $ f_{m}^{-1}\rightarrow f^{-1} $, 其中 $ \tilde{I}:=[\tilde{\alpha},\tilde{\beta}] $, $ \tilde{\alpha},\tilde{\beta}\in \mathbb{R} $, $ C(\tilde{I}) $ 是一个赋予上确界范数 $ \|f\|:=\sup\limits_{x\in \tilde{I}} |f(x)| $ 的 Banach 空间.

注意: 如果序列 $ (f_{m})_{m\in \mathbb{N}}\subset C(\tilde{I},\tilde{I}) $ 满足 $ \lim\limits_{m\rightarrow\infty}f_{m}=f $, 则

进一步, 如果 $ f $ 和 $ f_{m} $ ( $ m\in \mathbb{N}) $ 都在类 $ H(\tilde{I},\tilde{I}) $ 中, 则

在这一节中, 我们关注方程 (1.3) 的递增同胚解.

令

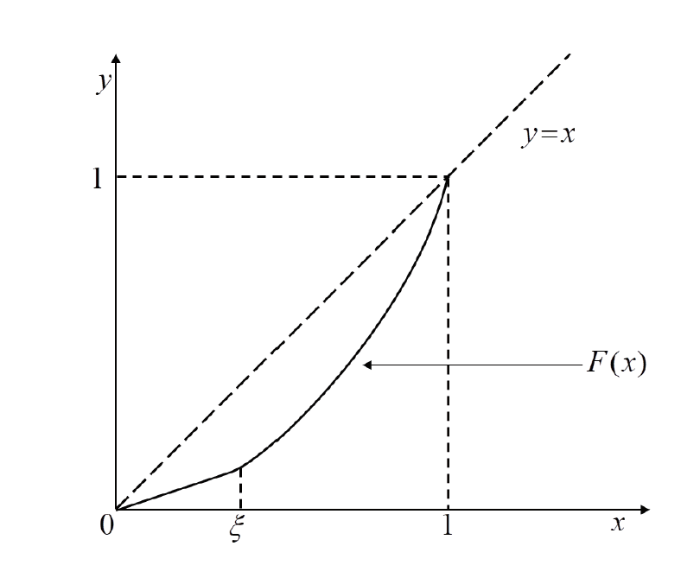
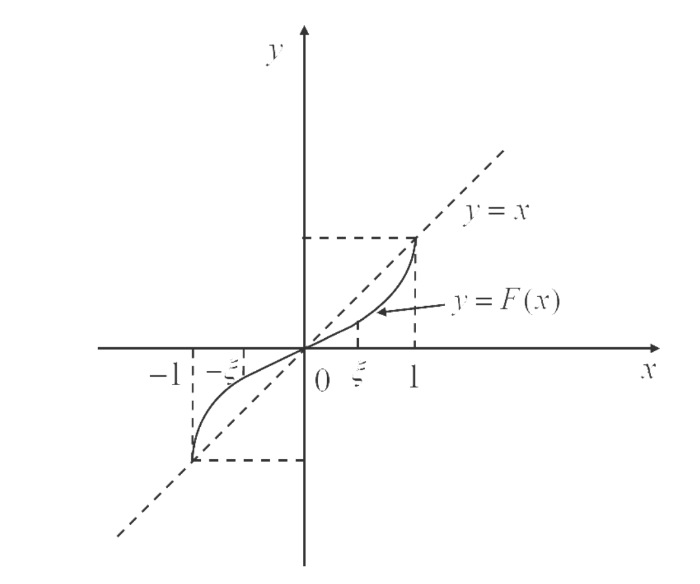
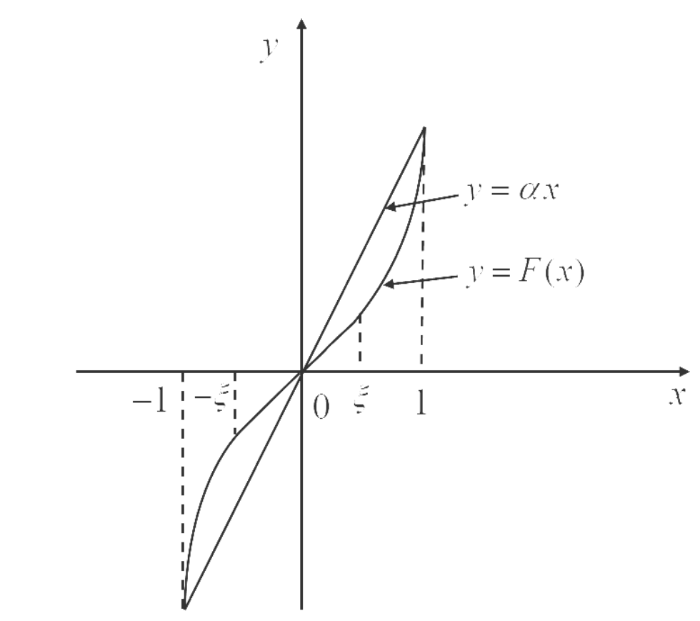
$ \mathcal{R}^{\xi}[J]:=\{F\in H_{+}(J, J)| F(x)-x<0, \forall x\in (0,1) $ 且 $ F $ 在 $ [\xi], \xi\in (0, 1) $ 上是线性的 $ \} $ (见图 1).

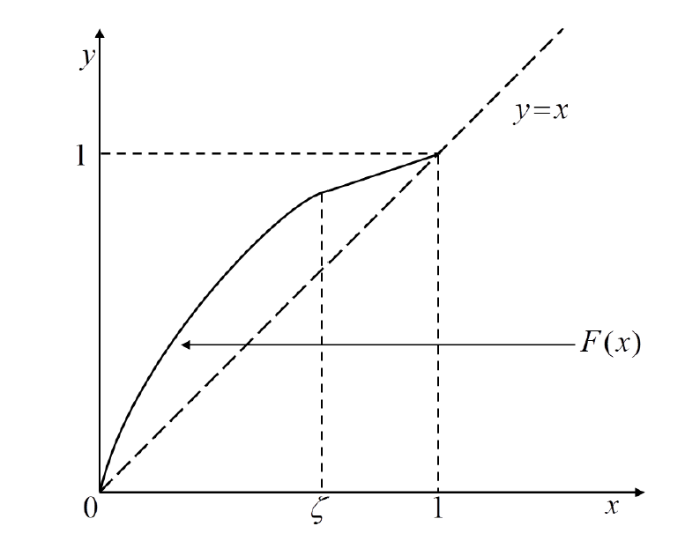
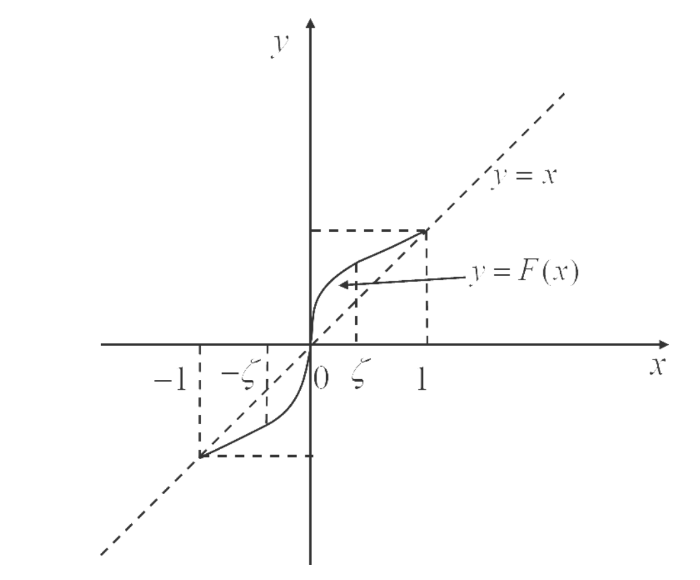
$ \mathcal{S}^{\zeta}[J]:=\{F\in H_{+}(J, J)| F(x)-x>0, \forall x\in (0,1) $ 和 $ F $ 在 $ [\zeta], \zeta\in (0, 1) $ 上是线性的 $ \} $ (见图 2).

显然, $ \mathcal{R}^{\xi}[J] $ 和 $ \mathcal{S}^{\zeta}[J] $ 是两个局部线性函数的集合.

我们定义一个比上面更一般的集合

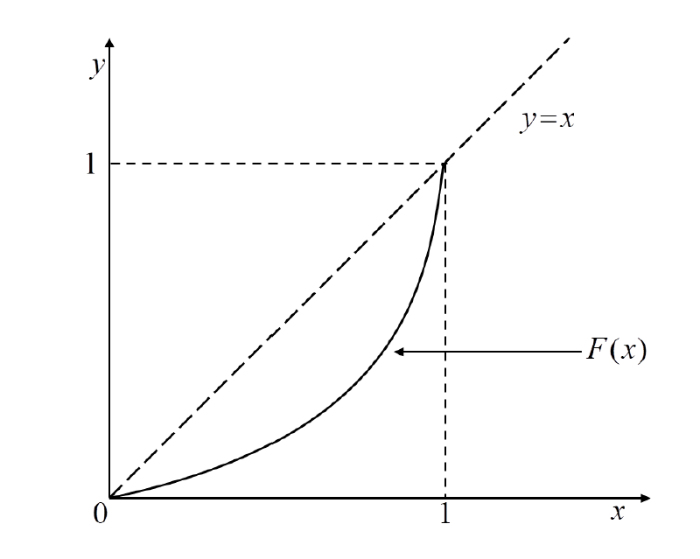
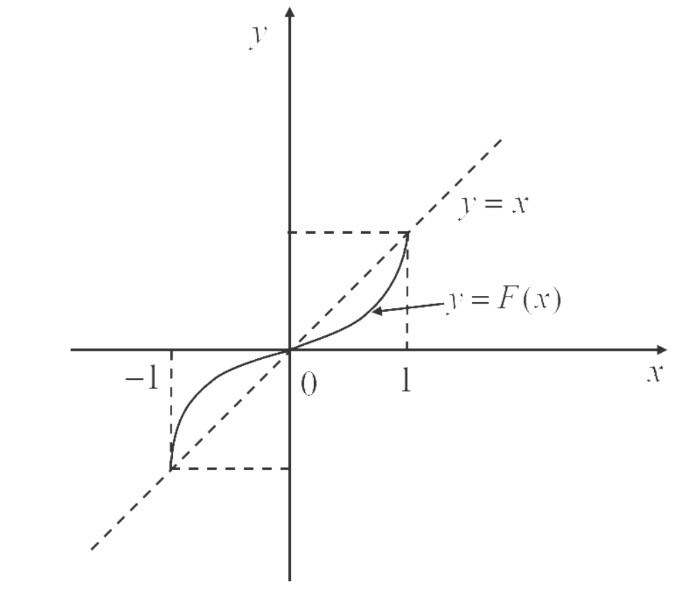
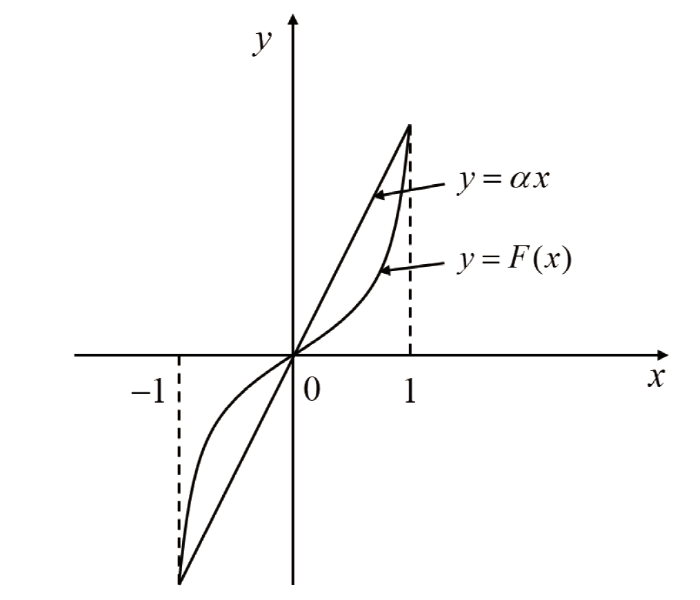
$ \mathcal{R}[J]:=\{F\in H_{+}(J, J)| F(x)-x<0, \forall x\in (0,1)\} $ (见图 3).

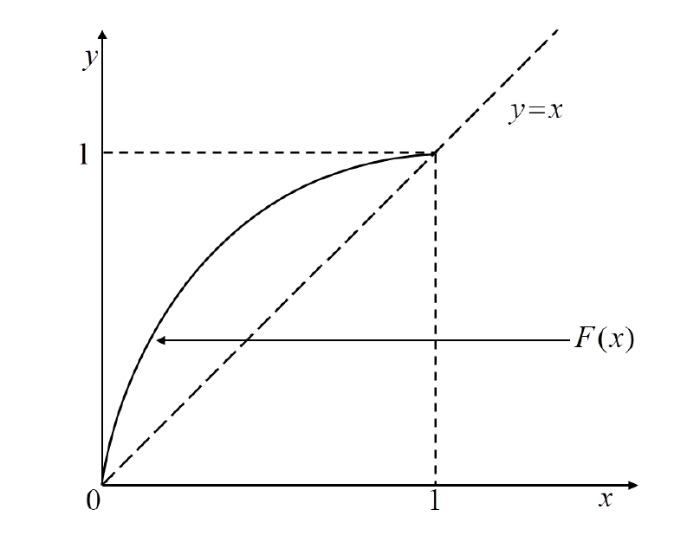
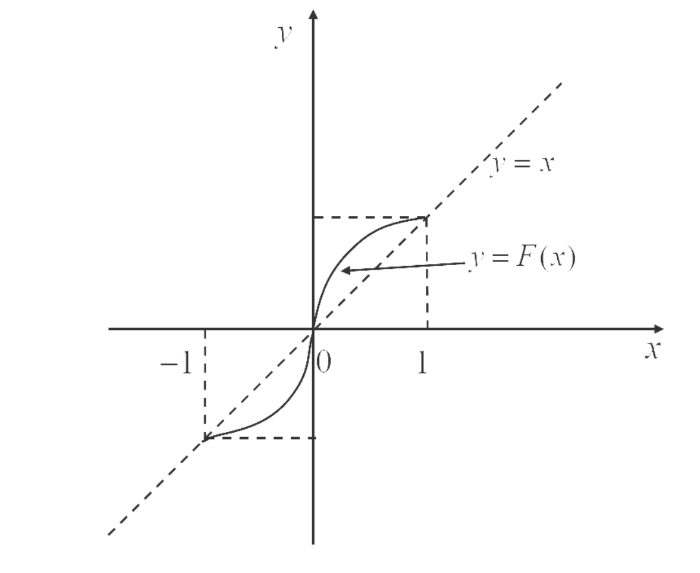
$ \mathcal{S}[J]:=\{F\in H_{+}(J, J)| F(x)-x>0, \forall x\in (0,1)\} $ (见图 4).

注3.1 注意函数 $ \tilde{F}\in\mathcal{S}^{\zeta}[J] $ (或者 $ \mathcal{S}[J] $) 通过变换 $ F(x)=1-\tilde{F}(1-x) $, 其中 $ \xi=1-\zeta $, 能转化为 $ F\in\mathcal{R}^{\xi}[J] $ (或者 $ \mathcal{R}[J] $). 因此, 我们只需考虑集合 $ \mathcal{R}^{\xi}[J] $ 和集合 $ \mathcal{R}[J] $.

下面我们首先考虑在 $ G\in M(J^{n}) $ 和 $ F\in \mathcal{R}^{\xi}[J] $ 情形下, 方程 (1.3) 的递增同胚解.

定理3.1 若 $ G\in M(J^{n}) $ 和 $ F\in \mathcal{R}^{\xi}[J] $, 则方程 (1.3) 有依赖参数 $ \xi $ 的解.

证 首先, 我们求出方程 (1.3) 在区间 $ [0, \xi) $ 上的线性解. 因为 $ F\in \mathcal{R}^{\xi}[J] $, 所以 $ F $ 在区间 $ [0, \xi) $ 上可以表示为 $ F(x)=cx, x\in [0, \xi) $, 其中 $ c\in (0,1) $ 是一个固定常数. 此外, 注意 $ G\in M(J^{n}) $, 这样函数

恰好有一个正根 $ s_{1}\in (0, 1) $. 这是根据 $ G $ 的连续性以及 $ G(0, 0,\cdot\cdot\cdot, 0)=0 $ 和 $ G(1, 1,\cdot\cdot\cdot, 1)=1 $ 所得到. 设 $ \bar{f}(x):=s_{1}x, x\in [0,\xi) $. 显然 $ \bar{f} $ 是一个自映射. 对于每个 $ n\in\mathbb{N} $, $ \bar{f}^{n}(x)=s_{1}^{n}x, x\in [0,\xi) $. 因为 $ G $ 是齐次的且 $ s_{1} $ 是 (3.1) 式定义的函数 $ \rho $ 的一个根, 所以我们有

这样, 函数 $ \bar{f}(x)=s_{1}x $ 是方程 (1.3) 在 $ [0,\xi) $ 上的解.

接下来, 我们将 $ [0,\xi) $ 上的解延拓到整个区间 $ [0,1] $ 上. 为了这个目的, 我们需要构造一个序列去划分区间 $ [\xi,1] $. 定义 $ \bar{x}_{m}:=s_{1}^{m}\xi, m\geq1 $ 和

从 (3.1) 式我们可以看出

接下来, 我们证明序列 $ (\bar{x}_{-m}), m\geq0 $, 是严格递增的并且整个序列落在区间 $ (0,1) $ 上. 因为 $ 0<\bar{x}_{i}<\bar{x}_{i-1}<1, i=1,\cdot\cdot\cdot, n $, 以及函数 $ G $ 关于每个变量都是严格递增且满足 $ G(0, 0,\cdot\cdot\cdot, 0)=0, G(1, 1,\cdot\cdot\cdot, 1)=1 $, 所以可知

另外, $ F^{-1}: [0,1]\rightarrow [0,1] $ 是严格递增的. 这个条件联合 (3.2)-(3.3) 式又可以得出

这表明 $ 0<\bar{x}_{0}<\bar{x}_{-1}<1. $ 通过对 $ m $ 用归纳法, 我们能证明序列 $ (\bar{x}_{-m}), m\geq0 $ 满足 $ 0<\xi=\bar{x}_{0}<\bar{x}_{-1}<\cdot\cdot\cdot<\bar{x}_{-m}<\cdot\cdot\cdot<1, $ 这一点意味着 $ \lim\limits_{m\rightarrow\infty}\bar{x}_{-m}=1 $. 事实上, 如果 $ \lim\limits_{m\rightarrow\infty}\bar{x}_{-m}=b\in (\xi,1) $, 在 (3.2) 式两边让 $ m\rightarrow\infty $, 我们就可以得到

这与 $ F(x)<x, x\in(0,1) $ 发生矛盾. 所以

定义函数 $ \bar{f}_{i}: J_{i}\rightarrow J_{i+1} $ 且满足 $ \bar{f}_{i}(x)=\bar{f}(x), i=0,\cdot\cdot\cdot, n-2 $.

进一步，归纳地定义函数 $ \bar{f}_{-m} $ 和函数 $ \Phi_{-m} $ 如下

其中 $ m\in \mathbb{N}, y\in J_{-m+1}, x\in J_{-m} $. 接下来, 我们断定对每个 $ m\geq 1 $, 函数 $ \bar{f}_{-m} $ 是一个从 $ J_{-m} $ 到 $ J_{-m+1} $ 的保向同胚, 也就是,

(i) $ \bar{f}_{-m} $ 是有定义的, 在 $ J_{-m} $ 上连续并且严格递增, 且

(ii) $ \bar{f}_{-m}(\bar{x}_{-m})=\bar{x}_{-m+1} $, $ f_{-m}(\bar{x}_{-m+1})=\bar{x}_{-m+2} $.

当 $ m=1 $ 时, 从 (3.4) 式我们可以推断出

这个结论联系 $ \bar{f}_{i}(x)=\bar{f}(x)=s_1x $ 和 $ \bar{x}_{m}=s_{1}^{m}\xi, i=0,\cdot\cdot\cdot, n-2 $ 有

从 (3.2) 式可以推出 $ \Phi_{-1}(\bar{x}_{0})=\bar{x}_{-1} $ 与 $ \Phi_{-1}(\bar{x}_{1})=\bar{x}_{0} $. 此外, 由于 $ G $ 和 $ F^{-1} $ 的严格单调性, 函数 $ \bar{f}_{-1} $ 在 $ J_{-1} $ 上是有定义的, 连续且严格递增的并且满足 $ \bar{f}_{-1}(\bar{x}_{-1})=\bar{x}_{0} $ 和 $ \bar{f}_{-1}(\bar{x}_{0})=\bar{x}_{1} $. 因此,我们的论断就可以用归纳法证明.

最后, 定义

显然, 函数 $ f $ 在 $ J $ 上是有定义的, 由结论 (i)-(ii) 可以得出它是连续且严格递增的. 另外, 因为 $ f(1)=1, f(\bar{x}_{-m})=\bar{x}_{-m+1}, \bar{x}_{-m}\rightarrow0, m\rightarrow\infty $, 所以 $ f $ 在端点1也是连续的. 利用 (3.4)-(3.5) 式, 对于所有 $ m\geq1 $ 和 $ x\in J_{-m} $ 我们可以验证

因此, (3.5) 式定义的函数 $ f $ 在整个区间 $ J $ 上是方程 (1.3) 的严格递增同胚解. 证毕.

定理 3.1 关注的是 $ F $ 是局部线性条件下方程 (1.3) 的同胚解. 在这一节末尾, 我们继续研究非线性情况下方程的解.

引理3.1 若 $ G\in M(J^{n}) $, $ F\in H_{+}(J,J) $ 且 $ (F_{m})_{m\in \mathbb{N}}\subset H_{+}(J,J) $ 满足$ \lim\limits_{m\rightarrow\infty}F_{m}=F $. 如果对每一个 $ m\in \mathbb{N} $, $ f_{m}\in H_{+}(J,J) $ 是下面方程的一个解

那么序列 $ (f_{m})_{n\in \mathbb{N}} $ 有一个聚点 $ f\in H_{+}(J,J) $ 且满足方程(1.3).

证 因为对于每个 $ i=1,\cdot\cdot\cdot,n, m \in \mathbb{N} $, $ f_{m} $ s都是严格递增的, 所以我们有

此外, 对于每个 $ m\in\mathbb{N} $, 从 (3.6) 式可以推出

注意 $ G $ 关于每个变量都是严格递增的且满足条件 ({C}$_{2} $), 那么对于所有的 $ i=1,\cdot\cdot\cdot, n $, 我们可知

从而 (3.8)-(3.9) 式表明

根据 Ascoli-Arzela 引理, 从 $ \lim\limits_{m\rightarrow\infty}F_{m}=F $ 容易知道 $ (F_{m})_{m\in \mathbb{N}} $ 在 $ C(J) $ 中是等度连续的. 则不等式 (3.7)-(3.10) 表明对于 $ \varepsilon>0 $, 只要 $ x_{1},x_{2}\in I $ 且$ |x_{1}-x_{2}|<\delta(\varepsilon) $ 就存在一个常数 $ \delta(\varepsilon)>0 $ 使得 $ |f_{m}^{i}(x_{1})-f_{m}^{i}(x_{2})|<n|F_{m}(x_{1})-F_{m}(x_{2})|<\varepsilon. $ 因此, 对于每个 $ i=1,\cdot\cdot\cdot,n $, 序列 $ (f_{m}^{i})_{m\in\mathbb{N}} $ 是等度连续的. 注意 $ (f_{m}^{i})_{m\in\mathbb{N}} $ 也是一致有界的. 因此, 再一次应用 Ascoli-Arzela 引理, 这个序列在 $ C(J,J) $ 中有一个收敛的子序列 $ (f_{m_{\tau}}^{i})_{\tau\in\mathbb{N}} $.

另一方面, 因为 $ 1,\cdot\cdot\cdot, n $ 是互素的, 则存在 $ b_{1},\cdot\cdot\cdot, b_{n} $ 使得 $ b_{1}1+\cdot\cdot\cdot+b_{n}n=1 $. 从而

接下来我们断定对每一个 $ i=1,\cdot\cdot\cdot, n $ 都有

如果 (3.11) 式成立, 那么根据引理 2.1, 当 $ \tau\rightarrow\infty $ 时, $ f_{m_{\tau}} $ 在 $ H_{+}(J,J) $ 中存在极限. 设 $ f:=\lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}} $. 从方程 (3.6) 可知

在 (3.12) 式两边让 $ \tau $ 趋于 $ \infty $, 再次根据引理 2.1 我们又得到

因此 $ f\in H_{+}(J,J) $ 是方程 (1.3) 的解. 为了证明 (3.11) 式, 只需证明对每个 $ i=1,\cdot\cdot\cdot,n, \lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}^{i} $ 是严格递增的. 这里, 我们利用反证法, 假若对某个 $ i $ 存在两个不同的点 $ x_{1},x_{2}\in I $ 使得 $ \lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}^{i}(x_{1})=\lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}^{i}(x_{2}) $. 不失一般性, 设

其中 $ q\in \{2,\cdot\cdot\cdot,n+1\} $ 和 $ \{i_{1},\cdot\cdot\cdot,i_{n}\} $ 是 $ \{1,\cdot\cdot\cdot,n\} $ 的一个排列. 若 $ q=n+1 $, 即 (3.13) 式对所有的 $ l=1,\cdot\cdot\cdot,n $ 都成立. 因为 $ G $ 关于每个变量都是连续且严格递增的, 利用方程 (3.12) 我们得到

这表明 $ \lim\limits_{\tau\rightarrow\infty}F_{m_{\tau}}(x_{1})=\lim\limits_{\tau\rightarrow\infty}F_{m_{\tau}}(x_{2}) $, 与 $ F=\lim\limits_{\tau\rightarrow\infty}F_{m_{\tau}} $ 是严格递增的事实发生矛盾.

如果 $ q\in \{2,\cdot\cdot\cdot,n\} $, 我们采用^[引理2]证明中的方法找一个合适的 $ \gamma\in\mathbb{N} $ 使得

然后重复上面的过程, 我们最终可以得到一个 $ \tilde{\gamma}\in\mathbb{N} $ 满足 $ f_{m_{\tau}}^{\tilde{\gamma}}(x_{1})\neq f_{m_{\tau}}^{\tilde{\gamma}}(x_{2}) $, 而对所有的 $ i=1, 2,\cdot\cdot\cdot, n $ 都满足 $ \lim\limits_{\tau\rightarrow\infty}f^{i+\tilde{\gamma}}_{m_{\tau}}(x_{1})=\lim\limits_{\tau\rightarrow\infty}f^{i+\tilde{\gamma}}_{m_{\tau}}(x_{2}) $. 然后, 将 (3.12) 式中的 $ x $ 用 $ f_{m_{\tau}}^{\tilde{\gamma}}(x) $ 替换, 得到下面的方程

显然

根据 $ G $ 和 $ F_{m_{\tau}} $ 的连续性以及条件 $ \lim\limits_{\tau\rightarrow\infty}F_{m_{\tau}}=F $ 有

因此, 借助 $ \lim\limits_{\tau\rightarrow\infty}f^{i+\tilde{\gamma}}_{m_{\tau}}(x_{1})=\lim\limits_{\tau\rightarrow\infty}f^{i+\tilde{\gamma}}_{m_{\tau}}(x_{2}), i=1, 2,\cdot\cdot\cdot, n $ 可得

这明显与 $ F $ 是严格递增的以及 $ \lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}^{\tilde{\gamma}}(x_{1})\neq\lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}^{\tilde{\gamma}}(x_{2}) $ 发生矛盾. 证毕.

利用定理 3.1 和引理 3.1, 我们得到本节的主要结论.

定理3.2 若 $ G\in M(J^{n}), F\in \mathcal{R}[J] $, 则方程 (1.3) 有解 $ f\in H_{+}(J,J) $.

证 设 $ F\in\mathcal{R}[J] $, $ (\xi_{m})_{m\in \mathbb{N}}\subset (0,1) $ 是一个满足 $ \lim\limits_{m\rightarrow\infty}\xi_{m}=0 $ 的序列. 对每一个 $ m\in \mathbb{N} $ 我们定义函数 $ F_{m}: J\to J $ 如下

其中 $ \kappa_{m}=\frac{F(\xi_{m})}{\xi_{m}} $. 容易看出 $ F_{m}\in \mathcal{R}^{\xi_{m}}[J] $ 且$ \lim\limits_{m\rightarrow\infty}F_{m}=F $. 所以根据定理 3.1 和引理 3.1, 我们得到方程 (1.3) 有一个解 $ f\in H_{+}(J,J) $. 证毕.

在这一节中, 我们主要考虑方程 (1.3) 的递减同胚解.

定义

$ \mathcal{W}^{\xi}[I]:=\{F\in H_{+}(I,I)| F(0)=0, x(F(x)-x)<0, \forall x\in (-1,0)\cup(0,1) $, $ F $ 在 $ [-\xi, \xi]$, $\xi \in (0, 1) $ 上是线性的 $ \} $ (见图 5),

$ \mathcal{V}^{\zeta}[I]=\{F\in H_{+}(I,I)| F(0)=0, x(F(x)-x)>0, \forall x\in (-1,0)\cup(0,1), F $ 在 $ [-1,-\zeta]\cup[\zeta,1], \zeta\in (0, 1) $ 上是线性的 $ \} $ (见图 6).

显然, 集合 $ \mathcal{W}^{\xi}[I] $ 和集合 $ \mathcal{V}^{\zeta}[I] $ 是由局部线性函数所构成. 类似地, 我们也考虑下面非线性函数构成的集合.

$ \mathcal{W}[I]:=\{F\in H_{+}(I,I)| F(0)=0, x(F(x)-x)<0, \forall x\in (-1,0)\cup(0,1)\} $ (见图 7).

$ \mathcal{V}[I]:=\{F\in H_{+}(I,I)| F(0)=0, x(F(x)-x)>0, \forall x\in (-1,0)\cup(0,1)\} $ (见图 8).

注4.1 注意: 每个函数 $ \tilde{F}\in\mathcal{V}^{\zeta}[I] $ (或者 $ \mathcal{V}[I] $) 通过变换 $ F(x)=1-\tilde{F}(1-x) $ 可以转化为 $ F\in\mathcal{W}^{\xi}[I] $ (或者 $ \mathcal{W}[I] $), 这里 $ \xi=1-\zeta $. 因此, 我们仅需处理 $ \mathcal{W}^{\xi}[I] $ 和 $ \mathcal{W}[I] $ 这两种集合的情形.

接下来, 我们首先研究局部线性的情况.

定理4.1 如果 $ G\in N(I^{n}), F\in \mathcal{W}^{\xi}[I] $, 那么方程 (1.3) 有一个依赖参数 $ \xi $ 的解 $ f\in H_{-}(I,I) $.

证 类似定理 3.1 中的证明, 设 $ F(x):=\tilde{c}x, x\in (-\xi, \xi) $, 这里 $ \tilde{c}\in (0,1) $ 是一个固定的常数. 则 $ \tilde{f}(x):=\tilde{r}_{1}x $ 是方程 (1.3) 在 $ [\tilde{r}_{1}\xi,\xi) $ 上的一个解, 其中 $ \tilde{r}_{1}\in (-1,0) $ 是下面方程的一个负根

接下来为了构造方程 (1.3) 在 $ (-1,\tilde{r}_{1}\xi]\cup[\xi,1) $ 上的解, 我们需要用一个序列划分区间 $ (-1,\tilde{r}_{1}\xi]\cup[\xi,1) $. 设 $ \tilde{x}_{m}:=\tilde{r}_{1}^{m}\xi, m\geq1 $. 定义

显然, 序列 $ (\tilde{x}_{-m}) $, $ m\geq 0 $ 是严格递增的并且 $ \lim\limits_{m\rightarrow\infty}\tilde{x}_{-2k+1}=-1 $, $ \lim\limits_{m\rightarrow\infty}\tilde{x}_{-2k}=1 $. 所以

这里当 $ j $ 为奇数时 $ I_{j}:=[\tilde{x}_{j},\tilde{x}_{j+2}] $, $ j $ 为偶数时 $ I_{j}:=[\tilde{x}_{j+2},\tilde{x}_{j}] $. 定义函数 $ \tilde{f}_{i}: I_{i}\rightarrow I_{i+1} $ 使得对所有 $ i=0,\cdot\cdot\cdot, n-2, $ 有 $ \tilde{f}_{i}(x)=\tilde{f}(x) $. 我们进一步归纳地定义函数 $ \tilde{f}_{-m} $ 和 $ \Psi_{-m} $ 如下

其中 $ m\in \mathbb{N}, y\in I_{-m+1}, x\in I_{-m} $. 显然对于 $ m\in \mathbb{N} $, 函数 $ \tilde{f}_{-m} $ 在 $ I_{-m} $ 上是有定义的连续严格递减函数. 最后定义

可以验证函数 $ f $ 是方程 (1.3) 在整个 $ I $ 上的一个递减同胚解. 证毕.

下面我们继续讨论方程 (1.3) 的非线性递减同胚解.

引理4.1 若 $ G\in N(I^{n}) $, $ F\in H_{+}(I,I) $, $ (F_{m})_{m\in \mathbb{N}}\subset H_{+}(I,I) $ 满足 $ \lim\limits_{m\rightarrow\infty}F_{m}=F $. 对每一个 $ m\in \mathbb{N} $, 设 $ f_{m}\in H_{-}(I,I) $ 是下面方程的一个解

则这个序列 $ (f_{m})_{n\in \mathbb{N}} $ 有一个聚点 $ f\in H_{-}(I,I) $ 且满足方程 (1.3).

证 因为 $ f_{m} $ 是严格递减的, 对每一个偶数 (或者奇数) $ i $ 以及 $ m\in \mathbb{N} $ 分别有

和

因为 $ G $ 满足条件 ({D}$_{1} $)-({D}$_{2} $), 回忆一下 ({D}$_{1} $) 是说 $ G $ 关于每个偶下标的变量是严格递增的而关于每个奇下标的变量是严格递减的, ({D}$_{2} $) 是对于所有满足 $ \vec{x}\succeq_{2}\vec{y} $ 的 $ \vec{x},\vec{y}\in I^{n} $ 都有 $ |G(\vec{x})-G(\vec{y})|\geq\|\vec{x}-\vec{y}\|_{*} $, 所以我们有

从 (4.1)-(4.2) 式可推出

因为 $ \lim\limits_{m\rightarrow\infty}F_{m}=F $, 根据 Ascoli-Arzela 引理, 序列 $ (F_{m})_{m\in \mathbb{N}} $ 在 $ C(I) $ 上是等度连续的. 此外不等式 (4.3) 表明对每一个 $ i=1,\cdot\cdot\cdot,n $, 序列 $ (f_{m}^{i})_{m\in\mathbb{N}} $ 是等度连续且一致有界. 再一次利用 Ascoli-Arzela 引理, 这个序列在 $ C(I,I) $ 上有一个收敛的子序列 $ (f_{m_{\tau}}^{i})_{\tau\in\mathbb{N}} $. 最后, 利用引理 3.1 中的证明方法可知 $ f:=\lim\limits_{\tau\rightarrow\infty}f_{m_{\tau}}\in H_{-}(I,I) $ 是方程(1.3)的解. 证毕.

定理4.2 若 $ G\in N(I^{n}), F\in \mathcal{W}[I] $. 则方程 (1.3) 有一个解 $ f\in H_{-}(I,I) $.

证 设 $ F\in\mathcal{W}[I] $, $ (\xi_{m})_{m\in \mathbb{N}}\subset (0,1) $ 是一个满足$ \lim\limits_{m\rightarrow\infty}\xi_{m}=0 $ 的序列. 对每一个 $ m\in \mathbb{N} $ 我们定义函数 $ F_{m}\in \mathcal{W}[I] $ 如下

其中 $ \lambda_{m}=\frac{F(\xi_{m})-F(-\xi_{m})}{2\xi_{m}} $. 显然 $ \lim\limits_{m\rightarrow\infty}F_{m}=F $. 根据定理 4.1 和引理 4.1, 我们可知方程 (1.3) 有一个解 $ f\in H_{-}(I,I) $. 证毕.

在这一节, 我们将利用第三节和第四节的主要结论求解多项式型函数迭代方程 (1.4).

正如我们在引言中所说, 如果方程 (1.3) 中的函数 $ G $ 是线性的, 那么方程 (1.3) 就变成它的特殊情形方程 (1.4), 并且方程 (1.4) 的递增同胚解在文献 [32] 中已经研究过. 在这一节我们继续研究它的递减同胚解. 为了应用前面的主要结论, 我们需要下面的一些假设

进一步定义两类局部线性和非线性的函数.

$ \mathcal{P}_{\alpha}^{\xi}[I]:=\{F\in H_{+}(I,\alpha I)| F(0)=0, x(F(x)-\alpha x)<0, \forall x\in (-1,0)\cup(0,1), F $ 在 $ [-\xi, \xi], \xi\in (0, 1) $, 上是线性的 $ \} $ (见图 9),

$ \mathcal{P}_{\alpha}[I]:=\{F\in H_{+}(I,\alpha I)| F(0)=0, x(F(x)-\alpha x)<0, \forall x\in (-1,0)\cup(0,1)\} $ (见图 10), 其中 $ \alpha:=\sum\limits_{{\rm even} i}\alpha_{i}-\sum\limits_{{\rm odd} i}\alpha_{i} $. 显然根据 $ (\mathcal{H}) $ 可知 $ \alpha>0 $. 此外, $ \mathcal{P}^{\xi}_{\alpha}[I] $ 是一个局部线性函数的集合, 而 $ \mathcal{P}_{\alpha}[I] $ 是一个非线性函数的集合.

利用定理 4.1, 我们首先考虑方程 (1.4) 在区间 $ I $ 上的局部线性递减同胚解, 然后它的一般递减同胚解可以通过定理 4.2 得到.

推论5.1 若 $ (\mathcal{H}) $ 成立, 同时 $ F\in \mathcal{P}_{\alpha}^{\xi}[I] $, 则方程 (1.4) 有一个解 $ f\in H_{-}(I,I) $ 满足 $ f(0)=0 $ 且它在原点的某邻域是线性的.

推论 5.1 的证明与定理 4.1 的证明相似, 这里我们略去.

推论5.2 若 $ (\mathcal{H}) $ 成立并且 $ F\in \mathcal{P}_{\alpha}[I] $, 则方程 (1.4) 有一个解 $ f\in H_{-}(I,I) $.

证 为了方便起见, 我们去掉所有系数为 0 的项并重写方程 (1.4) 如下

其中 $ m_{1},\cdot\cdot\cdot,m_{k}\in\{1,\cdot\cdot\cdot, m\} $, $ (-1)^{m_{l}}\alpha_{m_{l}}>0, \forall l=1,\cdot\cdot\cdot,k $.

设 $ d:=(m_{1},\cdot\cdot\cdot, m_{k}) $. 如果 $ d\geq2 $ 是偶数, 那么

其中 $ \check{f}:=f^{d} $. 假设 $ \check{f}\in H_{-}(I,I) $ 是下面方程的一个解

因为 $ \check{f} $ 没有严格递减的偶数阶迭代根, 所以方程 (5.1) 没有严格递减解 $ f\in H_{-}(I,I) $. 另一方面, 如果 $ d\geq3 $ 是奇数, 则根据文献 [p427] 可以得到 $ \check{f} $ 的所有 $ d $ 阶严格递减的迭代根 $ f\in H_{-}(I,I) $, 它们正是方程 (5.2) 的解. 因此, 我们仅仅需要考虑 $ d=1 $ 的情况.

设 $ F\in\mathcal{P}_{\alpha}[I] $, $ (\xi_{m})_{m\in \mathbb{N}}\subset (0,1) $ 是一个满足条件 $ \lim\limits_{m\rightarrow\infty}\xi_{m}=0 $ 的序列. 对每一个 $ m\in \mathbb{N} $ 我们定义函数 $ F_{m}\in \mathcal{P}_{\alpha}^{\xi_{m}}[I] $ 如下

其中 $ \chi_{m}=\frac{F(\xi_{m})-F(-\xi_{m})}{2\xi_{m}} $. 显然 $ \lim\limits_{m\rightarrow\infty}F_{m}=F $. 根据定理 4.2 的证明, 我们可知方程 (5.1)有解 $ f\in H_{-}(I,I) $. 证毕.

例5.1 考虑方程

显然 $ \alpha=\alpha_2+\alpha_4-\alpha_1-\alpha_3=4 $ 并且 $ F(x):=4x^{3}\in \mathcal{P}_{4}[I] $. 因此, 方程 (5.3) 有一个解 $ f\in H_{-}(I,I) $.