数学物理学报, 2024, 44(1): 37-49

周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近

何娅,, 安静,*

贵州师范大学数学科学学院 贵阳 550025

An Effective Fourier Spectral Approximation for Fourth-Order Eigenvalue Problems with Periodic Boundary Conditions

He Ya,, An Jing,*

School of Mathematical Sciences, Guizhou Normal University, Guiyang 550025

通讯作者: 安静, E-mail:aj154@163.com

收稿日期: 2022-09-6   修回日期: 2023-08-25  

基金资助: 国家自然科学基金项目(12061023)(Guizhou Science)
贵州省科技计划项目(黔科合平台人才[2017]5726-39)
贵州师范大学学术新苗基金项目(黔师新苗[2021]A04)

Received: 2022-09-6   Revised: 2023-08-25  

Fund supported: National Natural Science Foundation of China(12061023)
Guizhou Province Science and Technology Planning Project(Guizhou Science)
Guizhou Province Science and Technology Planning Project(Technology Cooperation Platform Talents [2017]5726-39)
Guizhou Normal University Academic New Talent Foundation(Qian Teacher New Talent [2021]A04)

作者简介 About authors

何娅,E-mail:Hy10190726@163.com

摘要

文章提出了周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近方法. 首先, 根据周期边界条件引入了适当的 Sobolev 空间和相应的逼近空间, 建立了原问题的一种弱形式及其离散格式, 并推导了等价的算子形式. 其次, 定义了正交投影算子, 并证明了其逼近性质, 结合紧算子的谱理论证明了逼近特征值的误差估计. 另外, 构造了逼近空间中的一组基函数, 推导了离散格式基于张量积的矩阵形式. 最后, 文章给出了一些数值算例, 数值结果表明其算法是有效的和谱精度的.

关键词： 周期边界; 四阶特征值问题; Fourier 谱方法; 误差估计

Abstract

In this paper, we put forward an effective Fourier spectral approximation method for fourth-order eigenvalue problems with periodic boundary conditions. Firstly, we introduce the appropriate Sobolev space and the corresponding approximation space according to the periodic boundary conditions, establish a weak form of the original problem and its discrete form, and derive the equivalent operator form. Then we define an orthogonal projection operator and prove its approximation properties. Combined with the spectral theory of compact operators, we prove the error estimates of approximation eigenvalues. In addition, we construct a set of basis functions of the approximation space, and derive the matrix form based on tensor product associated with the discrete scheme. Finally, we provide some numerical examples, and the numerical results show our algorithm is effective and spectral accuracy.

Keywords： Periodic boundary; Fourth-order eigenvalue problem; Fourier spectral method; Error estimates

PDF (624KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

何娅, 安静. 周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近[J]. 数学物理学报, 2024, 44(1): 37-49

He Ya, An Jing. An Effective Fourier Spectral Approximation for Fourth-Order Eigenvalue Problems with Periodic Boundary Conditions[J]. Acta Mathematica Scientia, 2024, 44(1): 37-49

1 引言

特征值问题在量子力学、流体力学、随机过程和结构力学等学科领域有着广泛的应用[6,7,13], 如机械振动模式结构的非线性弹性框架, 稳态的爱因斯坦凝聚[14]和基态电子结构[18,23]等. 关于特征值问题的数值方法已经有很多研究成果, 主要包括有限元法[11,16,17,20], 谱方法[3,4,9,10,19,22], 有限差分法[15]. 近年来, 关于四阶问题的高精度数值方法引起了很多学者的关注, 文献[1]提出了圆、球、椭圆域上双调和特征值问题的一种谱-Galerkin 方法; 文献[8]提出了固支板、紧支板和 Cahn-Hilliard 类型三种边界条件下双调和特征值问题基于 Legendre-Galerkin 逼近的一种直接谱方法; 文献[2]提出了球域上双调和特征值问题基于极小极大原理的一种高精度谱方法.

然而, 据我们所知, 很少有关于周期边界条件的四阶特征值问题的 Fourier 谱逼近的报道. 因此, 本文的目的是提出周期边界条件下四阶特征值问题的一种有效的 Fourier 谱逼近方法. 首先, 我们根据周期边界条件引入了适当的 Sobolev 空间和相应的逼近空间, 建立了原问题的一种弱形式及其离散格式, 并推导了等价的算子形式. 其次, 我们定义了正交投影算子, 并证明了其逼近性质, 结合紧算子的谱理论证明了逼近特征值的误差估计. 另外, 我们构造了逼近空间中的一组基函数, 推导了离散格式基于张量积的矩阵形式. 最后, 我们给出了一些数值算例, 数值结果表明我们的算法是有效的和谱精度的.

本文剩余部分组织如下: 在第 2 节我们推导了周期边界条件下四阶特征值问题的弱形式及其离散格式; 在第 3 节我们证明了逼近特征值的误差估计; 在第 4 节我们详细描述了算法的实现过程; 在第 5 节我们给出了一些数值算例.

2 弱形式及其离散格式

作为一个模型, 我们考虑如下的四阶特征值问题

$\Delta^2u-\nabla(\alpha\nabla u)+\beta u=\lambda u, \ \ \ \ \ \ \ \ \ (x,y)\in \Omega,$
$u(x,y)=u(x+L_x,y),\partial_{x}u(x,y)=\partial_{x}u(x+L_x,y),\ \ \ \ \ \ \ \ \ (x,y)\in \Omega,$
$u(x,y)=u(x,y+L_y),\partial_{y}u(x,y)=\partial_{y}u(x,y+L_y),\ \ \ \ \ \ \ \ \ (x,y)\in \Omega,$

其中$\alpha$是一个非负有界的$(L_x,L_y)$周期函数,$\beta$是一个有界函数,$\Omega=(x_L,x_R)\times(y_L,y_R), L_x=x_R-x_L, L_y=y_R-y_L$. 下面将推导 (2.1)-(2.3) 式的弱形式及其离散格式, 用$H^s(\Omega)$表示$s$阶 Sobolev 空间,$\|\cdot\|_{s,\Omega}$和$|\cdot|_{s,\Omega}$分别表示$H^s(\Omega)$中的范数和半范数. 特别地, 我们有

$H^0(\Omega)=L^2(\Omega)=\left\{u:\int_{\Omega} |u|^2 {\rm d}x{\rm d}y<\infty\right\},$

相应的内积和范数分别是

$(u,v)=\int_\Omega u\bar{v}{\rm d}x{\rm d}y,\|u\|=\bigg(\int_\Omega |u|^2{\rm d}x{\rm d}y\bigg)^{\frac{1}{2}}.$

定义Sobolev空间

$H_p^2(\Omega)=\left\{u\in H^2(\Omega):u \text{ 满足周期边界条件 (2.2)-(2.3)}\right\},$

相应的内积和范数分别为

$(u,v)_{2,\Omega}=\sum\limits_{|{\alpha}|=0}^2\int_\Omega D^{{\alpha}} uD^{{\alpha}} \bar{v} {\rm d}x{\rm d}y,\|u\|_{2,\Omega}=\bigg(\sum\limits_{|{\alpha}|=0}^2\|D^{{\alpha}} u\|^2\bigg)^\frac{1}{2},$

其中

${\alpha}=(\alpha_1,\alpha_2),|{\alpha}|=\alpha_1+\alpha_2,D^{{\alpha}}=\frac{\partial^{|{\alpha}|}}{\partial x^{\alpha_1}\partial y^{\alpha_2}}.$

由格林公式可知 (2.1)-(2.3) 式的弱形式为: 找$\lambda\in \mathbb{C}$,$0\neq u\in H_p^2(\Omega)$, 使得

$\begin{matrix} a(u,v)=\lambda b(u,v),\quad \forall v\in H_p^2(\Omega), \end{matrix}$

其中

$\begin{align*} a(u,v)&=\int_{\Omega}\Delta u\Delta \bar{v}{\rm d}x{\rm d}y+\int_{\Omega}\alpha\nabla u\nabla\bar{v}{\rm d}x{\rm d}y+\int_{\Omega}\beta u\bar{v}{\rm d}x{\rm d}y,\\ b(u,v)&=\int_{\Omega}u\bar{v}{\rm d}x{\rm d}y. \end{align*}$

定义如下的逼近空间

$X_{\scriptscriptstyle{M}}(\Omega)=\text{span}\Big\{{\rm e}^{{\rm i}2\pi k\frac{x-x_L}{L_x}}{\rm e}^{{\rm i}2\pi j\frac{y-y_L}{L_y}}, |k|=0,1,\cdots,M, |j|=0,1,\cdots,M\Big\}.$

则弱形式(2.4)相应的离散格式为: 找$\lambda_M\in\mathbb{C}$,$0\neq u_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)$, 使得

$\begin{matrix}a(u_{\scriptscriptstyle{M}},v_{\scriptscriptstyle{M}})=\lambda_{\scriptscriptstyle{M}} b(u_{\scriptscriptstyle{M}},v_{\scriptscriptstyle{M}}),\quad \forall v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega).\end{matrix}$

3 误差估计

在这一节, 我们将证明逼近特征值的误差估计, 由于$\alpha$是一个非负有界的$(L_x,L_y)$周期函数, 则有

$\begin{matrix}&\alpha_\ast:=\inf\limits_{(x,y)\in \Omega}\alpha(x,y)\geq0, \alpha^\ast:=\sup\limits_{(x,y)\in \Omega}\alpha(x,y)<\infty.\end{matrix}$

由于$\beta(x,y)$是一个有界函数, 不妨假设$\beta(x,y)$满足下面的条件

$\begin{matrix} &\beta_\ast:=\inf\limits_{(x,y)\in \Omega}\beta(x,y)>0, \beta^\ast:=\sup\limits_{(x,y)\in \Omega}\beta(x,y)<\infty.\end{matrix}$

事实上, 当$\beta(x,y)\leq0$, 我们只需要将方程 (2.1) 化为如下的等价形式

$\begin{align*} &\Delta^2u-\nabla(\alpha\nabla u)+\hat{\beta} u=\hat{\lambda }u, \end{align*}$

其中$\hat{\beta}=\beta+K, \hat{\lambda }=\lambda +K$, 则只要$K$足够大,$\hat{\beta}$自然能够满足条件(2.1).不失一般性, 令

$\begin{align*} x_L=y_L=0,x_R=y_R=2\pi, \end{align*}$

则$L_x=L_y=2\pi$,$\Omega=(0,2\pi)\times(0,2\pi)$. 为了叙述方便, 我们用$a\lesssim b$表示$a\leq Cb$, 其中$C$为大于零的常数.

引理 3.1$\forall u,v\in H_p^2(\Omega)$, 则下列等式成立

$\begin{align*}\int_\Omega \partial_{xy}u\partial_{xy}\bar{u}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}u\partial_{yy}\bar{u}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}\bar{u}\partial_{yy}u{\rm d}x{\rm d}y,\\\int_\Omega \partial_{xy}u\partial_{xy}\bar{v}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}u\partial_{yy}\bar{v}{\rm d}x{\rm d}y=\int_\Omega \partial_{yy}u\partial_{xx}\bar{v}{\rm d}x{\rm d}y.\end{align*}$

证 由分部积分公式有

$\begin{align*}\int_\Omega \partial_{xy}u\partial_{xy}\bar{u}{\rm d}x{\rm d}y&=\int_0^{2\pi} \partial_{xy}u\partial_{y}\bar{u}|_{x=0}^{x=2\pi}{\rm d}y-\int_\Omega \partial_{xxy}u\partial_{y}\bar{u}{\rm d}x{\rm d}y\\&=\int_0^{2\pi}\partial_{xy}u\partial_{y}\bar{u}|_{x=0}^{x=2\pi}{\rm d}y-\int_0^{2\pi}\partial_{xx}u\partial_{y}\bar{u}|_{y=0}^{y=2\pi}dx+\int_\Omega \partial_{xx}u\partial_{yy}\bar{u}{\rm d}x{\rm d}y,\end{align*}$

由周期边界条件 (2.2)-(2.3) 可得

$\partial_{xy}u(x,y)=\partial_{xy}u(x+2\pi,y),\partial_{y}\bar{u}(x,y)=\partial_{y}\bar{u}(x+2\pi,y),$
$\partial_{xx}u(x,y)=\partial_{xx}u(x,y+2\pi),\partial_{y}\bar{u}(x,y)=\partial_{y}\bar{u}(x,y+2\pi).$

则有

$\partial_{xy}u\partial_{y}\bar{u}|_{x=0}^{x=2\pi}=0,\partial_{xx}u\partial_{y}\bar{u}|_{y=0}^{y=2\pi}=0.$

因此

$\int_\Omega\partial_{xy}u\partial_{xy}\bar{u}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}u\partial_{yy}\bar{u}{\rm d}x{\rm d}y.$

将上式两边取共轭可得

$\int_\Omega\partial_{xy}u\partial_{xy}\bar{u}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}\bar{u}\partial_{yy}u{\rm d}x{\rm d}y.$

同理可证

$\int_\Omega \partial_{xy}u\partial_{xy}\bar{v}{\rm d}x{\rm d}y=\int_\Omega \partial_{xx}u\partial_{yy}\bar{v}{\rm d}x{\rm d}y=\int_\Omega \partial_{yy}u\partial_{xx}\bar{v}{\rm d}x{\rm d}y.$

证毕.

引理 3.2$\forall u\in H^2_p(\Omega)$, 则下列不等式成立

$\begin{align*}&\int_\Omega|\partial_xu|^2{\rm d}x{\rm d}y\leq \frac{1}{2}\|u\|^2+\frac{1}{2}\int_\Omega|\partial_{xx}u|^2{\rm d}x{\rm d}y,\\&\int_\Omega|\partial_yu|^2{\rm d}x{\rm d}y\leq \frac{1}{2}\|u\|^2+\frac{1}{2}\int_\Omega|\partial_{yy}u|^2{\rm d}x{\rm d}y.\end{align*}$

证 由 Cauchy-Schwarz 不等式和均值不等式有

$\begin{align*}\int_\Omega|\partial_xu|^2{\rm d}x{\rm d}y&=\int_0^{2\pi}\int_0^{2\pi}\partial_xu\partial_x\bar{u}{\rm d}x{\rm d}y=\int_0^{2\pi}u\partial_x\bar{u}|_{x=0}^{x=2\pi}{\rm d}y-\int_0^{2\pi}\int_0^{2\pi}u\partial_{xx}\bar{u}{\rm d}x{\rm d}y\\&=-\int_0^{2\pi}\int_0^{2\pi}u\partial_{xx}\bar{u}{\rm d}x{\rm d}y\leq\bigg(\int_\Omega|u|^2{\rm d}x{\rm d}y\bigg)^{\frac{1}{2}}\bigg(\int_\Omega|\partial_{xx}u|^2{\rm d}x{\rm d}y\bigg)^{\frac{1}{2}}\\&\leq\frac{1}{2}\|u\|^2+\frac{1}{2}\int_\Omega|\partial_{xx}u|^2{\rm d}x{\rm d}y.\end{align*}$

同理可得

$\begin{align*}&\int_\Omega|\partial_yu|^2{\rm d}x{\rm d}y\leq \frac{1}{2}\|u\|^2+\frac{1}{2}\int_\Omega|\partial_{yy}u|^2{\rm d}x{\rm d}y.\end{align*}$

证毕.

定理 3.1 若$\alpha(x,y)$,$\beta(x,y)$分别满足条件(3.1)和(3.2), 则$a(u,v)$为定义在$H_p^2(\Omega)\times H_p^2(\Omega)$上的正定连续的双线性泛函, 即

$|a(u,v)|\leq M^*\|u\|_{2,\Omega}\|v\|_{2,\Omega}, a(u,u)\geq M_*\|u\|_{2,\Omega}^2,$

其中$M^*=\max\{1,\alpha^*,\beta^*\}$,$M_*=\frac{1}{2}\min\{1,\beta_*\}$.

证 由引理 3.1 可得

$\begin{align*}\int_\Omega\Delta u\Delta \bar{v}{\rm d}x{\rm d}y&=\int_\Omega(\partial_{xx}u\partial_{xx}\bar{v}+\partial_{xx}u\partial_{yy}\bar{v}+\partial_{yy}u\partial_{xx}\bar{v}+\partial_{yy}u\partial_{yy}\bar{v}){\rm d}x{\rm d}y\\&=\int_\Omega(\partial_{xx}u\partial_{xx}\bar{v}+2\partial_{xy}u\partial_{xy}\bar{v}+\partial_{yy}u\partial_{yy}\bar{v}){\rm d}x{\rm d}y.\end{align*}$

则由 Cauchy-Schwarz 不等式有

$\begin{align*}|a(u,v)|&=\bigg|\int_\Omega\Delta u\Delta \bar{v} {\rm d}x{\rm d}y+\int_\Omega \alpha\nabla u\nabla\bar{v}{\rm d}x{\rm d}y+\int_\Omega \beta u\bar{v}{\rm d}x{\rm d}y\bigg|\\&\leq \int_\Omega(|\partial_{xx}u\partial_{xx}v|+2|\partial_{xy}u\partial_{xy}v|+|\partial_{yy}u\partial_{yy}v)|{\rm d}x{\rm d}y\\&\quad\ +\alpha^*\int_\Omega(|\partial_xu\partial_xv|+|\partial_yu\partial_yv|){\rm d}x{\rm d}y+\beta^*\int_\Omega|uv|{\rm d}x{\rm d}y\\&\leq \max\{1,\alpha^*,\beta^*\}\|u\|_{2,\Omega}\|v\|_{2,\Omega}.\end{align*}$

另一方面, 由引理 3.2 有

$\begin{align*}a(u,u)&=\int_\Omega(\partial_{xx}u\partial_{xx}\bar{u}+2\partial_{xy}u\partial_{xy}\bar{u}+\partial_{yy}u\partial_{yy}\bar{u}){\rm d}x{\rm d}y\\& +\int_\Omega\alpha(\partial_xu\partial_x\bar{u}+\partial_yu\partial_y\bar{u}){\rm d}x{\rm d}y+\int_\Omega\beta u\bar{u}{\rm d}x{\rm d}y\\&\geq \int_\Omega(|\partial_{xx}u|^2+2|\partial_{xy}u|^2+|\partial_{yy}u|^2){\rm d}x{\rm d}y+\beta_*\int_\Omega |u|^2{\rm d}x{\rm d}y\\&\geq \min\{1,\beta_*\}\int_\Omega(|\partial_{xx}u|^2+2|\partial_{xy}u|^2+|\partial_{yy}u|^2+ |u|^2){\rm d}x{\rm d}y\\&\geq \frac{1}{2}\min\{1,\beta_*\}\|u\|_{2,\Omega}^2.\end{align*}$

证毕.

类似于定理 3.1 的证明, 我们有下面的定理

定理 3.2$b(u,v)$是定义在$L^2(\Omega)\times L^2(\Omega)$上的正定连续的双线性泛函, 即

$|b(u,v)|\leq \|u\|\|v\|, b(u,u)\geq\|u\|^2.$

根据定理 3.1, 定理 3.2 以及 Lax-Milgram 引理, 可以定义解算子$T:L^2(\Omega)\rightarrow H_p^2(\Omega)$, 使得

$\begin{equation}a(Tu,v)=b(u,v),\quad \forall v\in H_p^2(\Omega).\end{equation}$

则 (2.4) 式有如下等价的算子形式

$Tu=\lambda^{-1}u.$

定理 3.3 由 (3.3) 式定义的算子$T:H_p^2(\Omega)\rightarrow H_p^2(\Omega)$是一个紧算子.

证 在 (3.3) 式中取$v=Tu$, 由定理 3.1 可得

$M_*\|Tu\|_{2,\Omega}^2\leq a(Tu,Tu)=b(u,Tu)\leq\|u\|\|Tu\|_{2,\Omega},$

即

$\begin{equation} \|Tu\|_{2,\Omega}\leq M_*^{-1}\|u\|. \end{equation}$

假设$S$为$H_p^2(\Omega)$中的一个有界集, 由$H_p^2(\Omega)$紧嵌入$L^2(\Omega)$可知$S$为$L^2(\Omega)$中的列紧集, 再由 (3.5) 式可知$S$为$H_p^2(\Omega)$中的列紧集. 因此,$T:H_p^2(\Omega)\rightarrow H_p^2(\Omega)$是一个紧算子. 证毕.

考虑 (2.4) 式的共轭问题: 找$\lambda^*\in\mathbb{C}$,$0\neq u^*\in H_p^2(\Omega)$, 使得

$\begin{equation} a(v,u^*)=\overline{\lambda^*} b(v,u^*),\quad \forall v\in H_p^2(\Omega). \end{equation}$

定义相应的解算子$T^*:L^2(\Omega)\rightarrow H_p^2(\Omega)$, 使得

$\begin{equation} a(v,T^*u^*)=b(v,u^*),\quad \forall v\in H_p^2(\Omega). \end{equation}$

则 (3.6) 式有如下等价的算子形式

$\begin{equation} T^*u^*=(\lambda^{*})^{-1}u^*. \end{equation}$

由于

$a(Tu,v)=b(u,v)=a(u,T^*v),u,v\in H_p^2(\Omega),$

则$T^*$为$T$的共轭算子, 从而$T^*:H_p^2(\Omega)\rightarrow H_p^2(\Omega)$也是一个紧算子. 类似于算子$T$的定义, 我们引入相应的解算子:$T_M:L^2(\Omega)\rightarrow X_M(\Omega)$, 使得

$\begin{equation} a(T_Mu,v_M)=b(u,v_M),\quad\forall u\in L^2(\Omega), \forall v_M\in X_M(\Omega). \end{equation}$

显然$T_M:L^2(\Omega)\rightarrow X_M(\Omega)$是一个有限秩算子, 且 (2.5) 式有如下等价的算子形式

$\begin{equation} T_Mu_M=\lambda_M^{-1}u_M. \end{equation}$

定义投影算子$\Pi_{\scriptscriptstyle{M}}:H_p^2(\Omega)\rightarrow X_{\scriptscriptstyle{M}}(\Omega)$, 使得

$\begin{equation} a(u-\Pi_{\scriptscriptstyle{M}} u,v_M)=0,\quad \forall u\in H_p^2(\Omega), \forall v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega). \end{equation}$

引理 3.3 令$T$和$T_{\scriptscriptstyle{M}}$分别为 (3.3) 式和 (3.9) 式定义的有界线性算子, 则有

$T_{\scriptscriptstyle{M}}=\Pi_{\scriptscriptstyle{M}}T.$

证 由 (3.3), (3.9) 式和 (3.11) 式, 对$\forall u\in H_p^2(\Omega)$,$\forall v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)$, 有

$\begin{align*} a(\Pi_{\scriptscriptstyle{M}}Tu-T_{\scriptscriptstyle{M}}u,v_{\scriptscriptstyle{M}})&=a(\Pi_{\scriptscriptstyle{M}}Tu-Tu+T u-T_{\scriptscriptstyle{M}}u,v_{\scriptscriptstyle{M}})\\ &=a(\Pi_{\scriptscriptstyle{M}}Tu-Tu,v_{\scriptscriptstyle{M}})+a(T u-T_{\scriptscriptstyle{M}}u,v_{\scriptscriptstyle{M}}) =0. \end{align*}$

在上式中取$v_{\scriptscriptstyle{M}}=\Pi_{\scriptscriptstyle{M}}Tu-T_{\scriptscriptstyle{M}}u$可得

$a(\Pi_{\scriptscriptstyle{M}}Tu-T_{\scriptscriptstyle{M}}u,\Pi_{\scriptscriptstyle{M}}Tu-T_{\scriptscriptstyle{M}}u)=0.$

由定理 3.1 有

$T_{\scriptscriptstyle{M}}=\Pi_{\scriptscriptstyle{M}}T.$

证毕.

显然,$T_{\scriptscriptstyle{M}}|_{X_{\scriptscriptstyle{M}}(\Omega)}: X_{\scriptscriptstyle{M}}(\Omega)\rightarrow X_{\scriptscriptstyle{M}}(\Omega)$也是一个有限秩算子. 令

$\begin{align*} \xi_{{\scriptscriptstyle{M}}}=\sup\limits_{u\in H_p^2(\Omega),\|u\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\|Tu-v_{\scriptscriptstyle{M}}\|_{2,\Omega}. \end{align*}$

由于$X_M(\Omega)$在$H_p^2(\Omega)$中终归稠密, 且逐一包含, 则有

$\begin{matrix} \lim\limits_{M\rightarrow\infty}\xi_{\scriptscriptstyle{M}}=0.\end{matrix}$

定理 3.4 令$\|u\|_a=\sqrt{a(u,u)}$, 则下面的等式成立

$\begin{matrix} \lim\limits_{M\rightarrow \infty}\|T-T_{\scriptscriptstyle{M}}\|_{\mathcal{L}( H_p^2(\Omega), H_p^2(\Omega))}=0. \end{matrix}$

证 由算子的范数定义和定理 3.1 可得

$\begin{align*} \|T-T_{\scriptscriptstyle{M}}\|_{\mathcal{L}( H_p^2(\Omega), H_p^2(\Omega))}&=\sup\limits_{u\in H_p^2(\Omega),\|u\|_{2,\Omega}=1}\|(T-T_{\scriptscriptstyle{M}})u\|_{2,\Omega}\\ &\leq\sup\limits_{u\in H_p^2(\Omega),\|u\|_{2,\Omega}=1}\frac{1}{\sqrt{M_*}}\|Tu-\Pi_{\scriptscriptstyle{M}}Tu\|_{a}\\ &\leq\sup\limits_{u\in H_p^2(\Omega),\|u\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\frac{1}{\sqrt{M_*}}|T u-v_{\scriptscriptstyle{M}}\|_{a}\\ &\leq\sup\limits_{u\in H_p^2(\Omega),\|u\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\sqrt{\frac{M^*}{M_*}}\|T u-v_{\scriptscriptstyle{M}}\|_{2,\Omega}\\ &=\sqrt{\frac{M^*}{M_*}}\xi_{\scriptscriptstyle{M}}. \end{align*}$

由 (3.12) 式知结论成立. 证毕.

类似地, 由格林公式可知 (3.6) 式的离散格式为: 找$\lambda_M^*\in\mathbb{C}$,$0\neq u_M^*\in X_M(\Omega)$, 使得

$\begin{matrix} a(v,u_M^*)=\overline{\lambda_M^*} b(v,u_M^*),\quad \forall v\in X_M(\Omega). \end{matrix}$

定义相应的解算子$T_M^*:L^2(\Omega)\rightarrow X_M(\Omega)$, 使得

$\begin{matrix} a(v,T_M^*u^*)=b(v,u^*),\quad \forall u^*\in L^2(\Omega), \forall v\in H_p^2(\Omega). \end{matrix}$

由 (3.15) 式可知 (3.14) 式等价的算子形式为

$T_M^*u_M^*=\lambda_M^{*-1}u_M^*.$

我们用$\lambda$和$\mu$分别表示代数重数为$g$的特征值和$\lambda^{-1}-T$的陡度. 由

$ \lim\limits_{M\rightarrow \infty}\|T-T_{\scriptscriptstyle{M}}\|_{\mathcal{L}( H_p^2(\Omega), H_p^2(\Omega))} =0 $

可知$g$个特征值$\lambda_{j,M}\ (j=1,\cdots,g)$将收敛到$\lambda$. 令$\rho(T)$和$\sigma(T)$分别表示算子$T$的预解集和谱集. 定义谱投影

$E=\frac{1}{2\pi {\rm i}}\int_\Gamma\mathcal{ R}_z(T){\rm d}z, E_M=\frac{1}{2\pi {\rm i}}\int_\Gamma \mathcal{R}_z(T_M){\rm d}z,$

其中$\Gamma$属于$\rho(T)$, 且是以谱点$\lambda^{-1}$为中心, 不再含有其它谱点的一个圆,$\mathcal{R}_z(T)=(z-T)^{-1}$. 由文献[5]可知$E$是一个到相应于$\lambda^{-1}$和$T$的广义特征向量空间的投影, 即$\mathcal{R}(E)=\mathcal{N}((\lambda^{-1}-T)^\mu)$, 其中$\mathcal{R}$表示像集,$\mathcal{N}$表示零空间. 类似地,$E_M$是一个到相应于$\lambda_{j,M}^{-1}(j=1,2,\cdots,g)$和$T_M$的广义特征向量空间直和的投影,即$\mathcal{R}(E_M)=\sum\limits_{j=1}^{g}\mathcal{N}((\lambda_{j,M}^{-1}-T_M)^{\mu_{j}})$, 其中$\mu_j$是$\lambda_{j,M}^{-1}-T_M$的陡度. 对于共轭问题 (3.6) 和 (3.14), 我们能够类似地定义$E^*, \mathcal{R}(E^*)$,$E_M^*, \mathcal{R}(E_M^*)$.令

$\begin{align*} &\varepsilon_{{\scriptscriptstyle{M}}}(\lambda)=\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\|u-v_{\scriptscriptstyle{M}}\|_{2,\Omega},\\ &\varepsilon_{{\scriptscriptstyle{M}}}^*(\lambda^*)=\sup\limits_{u^*\in \mathcal{R}(E^*),\|u^*\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\|u^*-v_{\scriptscriptstyle{M}}\|_{2,\Omega}. \end{align*}$

则由文献[5,定理 8.2-8.3], 我们有下面的结果.

定理 3.5 存在一个常数$C$, 使得下列不等式成立

$\begin{align*} &|\lambda-(\frac{1}{g}\sum_{j=1}^g\lambda_{j,M}^{-1})^{-1}|\leq C\varepsilon_{{\scriptscriptstyle{M}}}(\lambda)\varepsilon_{{\scriptscriptstyle{M}}}^*(\lambda^*),\\ &|\lambda-\lambda_{j,M}|\leq C[\varepsilon_{{\scriptscriptstyle{M}}}(\lambda)\varepsilon_{{\scriptscriptstyle{M}}}^*(\lambda^*)]^{\frac{1}{\mu}}. \end{align*}$

定理 3.4 对$\forall u\in H_p^m(\Omega)$,$0\leq\sigma\leq m$, 则存在常数$C$, 使得下列不等式成立

$\|\Pi_{\scriptscriptstyle{M}}u-u\|_{\sigma,\Omega}\leq C M^{\sigma-m}|u|_{m,\Omega}.$

证 由于

$\begin{align*} D^{{\alpha}}(u-\Pi_{\scriptscriptstyle{M}}u)=D^{{\alpha}} \bigg(\sum\limits_{|k|>M, |j|>M}u_{kj}{\rm e}^{{\rm i}kx+ijy}\bigg) =\sum\limits_{|k|>M, |j|>M}(ik)^{\alpha_1}(ij)^{\alpha_2}u_{kj}{\rm e}^{{\rm i}kx+ijy}, \end{align*}$

对于$0\leq |{\alpha}|\leq\sigma\leq m$, 取$\alpha_1\leq m_1,\alpha_2\leq m- m_1$, 则有

$\begin{align*} \|D^{{\alpha}}(u-\Pi_Mu)\|^2&=(2\pi)^2\sum\limits_{|k|>M, |j|>M}k^{2\alpha_1}j^{2\alpha_2}|u_{kj}|^2\\ &=(2\pi)^2\sum\limits_{|k|>M,|j|>M}k^{2(\alpha_1-m_1)}j^{2[\alpha_2-(m-m_1)]}|u_{kj}|^2k^{2m_1}j^{2(m-m_1)}\\ &\leq (2\pi)^2M^{2(\alpha_1-m_1)}M^{2[\alpha_2-(m-m_1)]}\sum\limits_{|k|>M,|j|>M}|u_{kj}|^2k^{2m_1}j^{2(m-m_1)}\\ &\leq M^{2(|{\alpha}|-m)}\sum\limits_{|k|\geq0,|j|\geq0}(2\pi)^2|u_{kj}|^2k^{2m_1}j^{2(m-m_1)}\\ &\leq M^{2(\sigma-m)}\|D^mu\|^2. \end{align*}$

对$|{\alpha}|$从 0 到$\sigma$求和可知结论成立. 证毕.

定理 3.6 对$\forall u\in H_p^m(\Omega)$, 存在一个常数$C$, 使得下列不等式成立

$\varepsilon_{{\scriptscriptstyle{M}}}(\lambda)\leq C M^{2-m}\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}|u|_{m,\Omega},$
$\varepsilon_{{\scriptscriptstyle{M}}}^*(\lambda^*)\leq C M^{2-m}\sup\limits_{u^*\in \mathcal{R}(E^*),\|u^*\|_{2,\Omega}=1}|u^*|_{m,\Omega}.$

证 由引理 3.4 可得

$\begin{align*} \varepsilon_{{\scriptscriptstyle{M}}}(\lambda)&=\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}\inf\limits_{v_{\scriptscriptstyle{M}}\in X_{\scriptscriptstyle{M}}(\Omega)}\|u-v_{\scriptscriptstyle{M}}\|_{2,\Omega}\\ &\leq\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}\|u-\Pi_{\scriptscriptstyle{M}}u\|_{2,\Omega} \leq CM^{2-m}\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}|u|_{m,\Omega}. \end{align*}$

类似于 (3.16) 式证明, 我们能得到 (3.17) 式. 证毕.

作为定理 3.5 和定理 3.6 的直接结果, 我们有下面的误差估计.

定理 3.7 对$\forall u\in H_p^m(\Omega)$, 存在一个常数$C$, 使得下列不等式成立

$\begin{align*} &|\lambda-(\frac{1}{g}\sum_{j=1}^g\lambda_{j,M}^{-1})^{-1}|\leq C M^{2(2-m)}[K_m(u)K_m^*(u^*)],\\ &|\lambda-\lambda_{j,M}|\leq C M^{\frac{2(2-m)}{\mu}}[K_m(u)K_m^*(u^*)]^{\frac{1}{\mu}}, \end{align*}$

其中

$K_m(u)=\sup\limits_{u\in \mathcal{R}(E),\|u\|_{2,\Omega}=1}|u|_{m,\Omega}, K_m^*(u^*)=\sup\limits_{u^*\in \mathcal{R}(E^*),\|u^*\|_{2,\Omega}=1}|u^*|_{m,\Omega}.$

4 算法的有效实现

在这一节我们将详细描述算法的有效实现过程. 首先构造逼近空间中的一组基函数

$\begin{align*} \varphi_{kj}={\rm e}^{{\rm i}kx}{\rm e}^{{\rm i}jy},|k|=0,1,\cdots, M,|j|=0,1,\cdots, M. \end{align*}$

则逼近空间可表示为

$\begin{align*} X_{\scriptscriptstyle{M}}(\Omega)=\text{span}\{{\rm e}^{{\rm i}kx}{\rm e}^{{\rm i}jy}, |k|=0,1,\cdots,M, |j|=0,1,\cdots,M\}. \end{align*}$

我们将寻找

$\begin{matrix} u_{\scriptscriptstyle{M}}(x,y)=\sum_{|k|=0}^{M}\sum_{|j|=0}^{M} u_{kj}\varphi_{kj}. \end{matrix}$

令

$U=\left( \begin{array}{ccccccc} u_{\scriptscriptstyle{-M,-M}} & \cdots & u_{\scriptscriptstyle{-M,0}} & \cdots & u_{\scriptscriptstyle{-M,M}}\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ u_{\scriptscriptstyle{0,-M}} & \cdots & u_{\scriptscriptstyle{00}} & \cdots &u_{\scriptscriptstyle{0,M}}\\ \vdots &\ddots & \vdots & \ddots & \vdots\\ u_{\scriptscriptstyle{M,-M}} & \cdots & u_{\scriptscriptstyle{M,0}} & \cdots &u_{\scriptscriptstyle{M,M}}\\ \end{array} \right)_.$

用$\overline{U}$表示由$U$的列构成的长度为$(2M+1)^2$的列向量, 则对$v_{\scriptscriptstyle{M}}={\rm e}^{{\rm i}sx}{\rm e}^{{\rm i}ty}$,$|s|=0,1,\cdots,M$,$|t|=0,1,\cdots,M$, 有

$\begin{align*} & \int_0^{2\pi}\int_0^{2\pi} \Delta u_{\scriptscriptstyle{M}}\Delta \bar{v}_{\scriptscriptstyle{M}} {\rm d}x{\rm d}y \\ &=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj} \int_0^{2\pi}\int_0^{2\pi}\Delta({\rm e}^{{\rm i}kx}{\rm e}^{{\rm i}jy})\Delta({\rm e}^{-{\rm i}sx}{\rm e}^{-{\rm i}ty}) {\rm d}x{\rm d}y\\ &=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}(d_{sk}h_{tj}+e_{sk}f_{tj}+f_{sk}e_{tj}+h_{sk}d_{tj})\\ &=D(s,:)UH(t,:)^{T}+E(s,:)UF(t,:)^{T}+F(s,:)UE(t,:)^{T}+H(s,:)UD(t,:)^{T}\\ &=[H(t,:)\otimes D(s,:)+F(t,:)\otimes E(s,:)+E(t,:)\otimes F(s,:)+D(t,:)\otimes H(s,:)]\overline{U}, \end{align*}$

其中

$\begin{align*} & D=(d_{sk}), E=(e_{sk}), F=(f_{sk}), H=(h_{sk}),\\ &d_{sk}=2\pi k^2s^2\delta_{sk}, e_{sk}=2\pi k^2\delta_{sk}, f_{sk}=2\pi s^2\delta_{sk}, h_{sk}=2\pi \delta_{sk}, \end{align*}$

$\delta_{sk}$是克罗内克函数,$H(s,:)$表示矩阵$H=(h_{sk})$的第$s$行,$\otimes$表示矩阵的张量积, 即$H\otimes D=(h_{sk}D)$.

$\begin{align*} & \int_0^{2\pi}\int_0^{2\pi} \alpha(x,y)\nabla u_{\scriptscriptstyle{M}}\nabla\bar{v}_{\scriptscriptstyle{M}} {\rm d}x{\rm d}y\\ &=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}\int_0^{2\pi}\int_0^{2\pi} \alpha(x,y)\nabla({\rm e}^{{\rm i}kx}{\rm e}^{{\rm i}jy})\nabla({\rm e}^{-{\rm i}sx}{\rm e}^{-{\rm i}ty}) {\rm d}x{\rm d}y\\ & =\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}(ks+jt)\int_0^{2\pi}\int_0^{2\pi} \alpha(x,y) {\rm e}^{{\rm i}(k-s)x}{\rm e}^{{\rm i}(j-t)y} {\rm d}x{\rm d}y\\ &=L((t+M+1)+(2M+1)(s+M),:)\overline{U}, \end{align*}$

其中$L=(l_{sktj})$是矩阵,$l_{sktj}$为矩阵$L$第$(t+M+1)+(2M+1)(s+M)$行, 第$(j+M+1)+(2M+1)(k+M)$列的元素, 即

$l_{sktj}=(ks+jt)\int_0^{2\pi}\int_0^{2\pi} \alpha(x,y) {\rm e}^{{\rm i}(k-s)x}{\rm e}^{{\rm i}(j-t)y} {\rm d}x{\rm d}y.$
$\begin{align*} \int_0^{2\pi}\int_0^{2\pi} \beta(x,y) u_{\scriptscriptstyle{M}}\bar{v}_{\scriptscriptstyle{M}}{\rm d}x{\rm d}y &=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}\int_0^{2\pi}\int_0^{2\pi} \beta(x,y) {\rm e}^{{\rm i}(k-s)x}{\rm e}^{{\rm i}(j-t)y} {\rm d}x{\rm d}y\\ &=R((t+M+1)+(2M+1)(s+M),:)\overline{U}, \end{align*}$

其中$R=(r_{sktj})$是矩阵,$r_{sktj}$为矩阵$R$第$(t+M+1)+(2M+1)(s+M)$行, 第$(j+M+1)+(2M+1)(k+M)$列的元素, 即

$r_{sktj}=\int_0^{2\pi}\int_0^{2\pi} \beta(x,y) {\rm e}^{{\rm i}(k-s)x}{\rm e}^{{\rm i}(j-t)y}{\rm d}x{\rm d}y.$
$\begin{align*} \int_0^{2\pi}\int_0^{2\pi} u_{\scriptscriptstyle{M}}\bar{v}_{\scriptscriptstyle{M}}{\rm d}x{\rm d}y&=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}\int_0^{2\pi}\int_0^{2\pi} {\rm e}^{{\rm i}kx}{\rm e}^{{\rm i}jy}{\rm e}^{-{\rm i}sx}{\rm e}^{-{\rm i}ty} {\rm d}x{\rm d}y\\ &=\sum\limits_{|k|=0}^{M}\sum\limits_{|j|=0}^{M} u_{kj}h_{sk}h_{tj}=H(s,:)UH(t,:)^{T}\\ &=H(t,:)\otimes H(s,:)\overline{U}. \end{align*}$

由上面的等式可得离散格式 (2.5) 等价的矩阵形式为

$\begin{matrix} (H\otimes D+F\otimes E+E\otimes F+D\otimes H+L+R)\overline{U}=\lambda_{\scriptscriptstyle{M}}(H\otimes H)\overline{U}. \end{matrix}$

5 数值实验

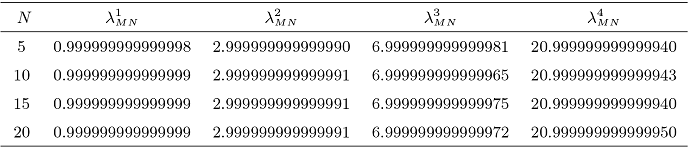
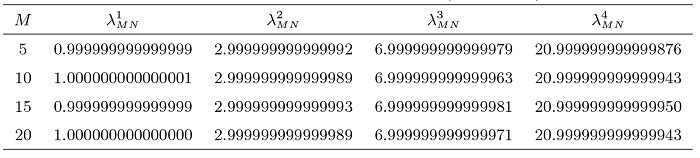
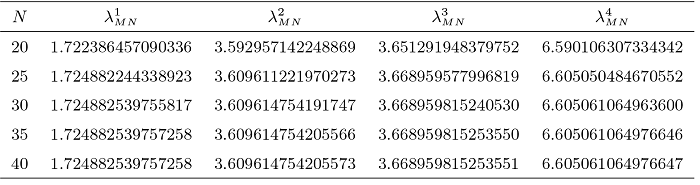
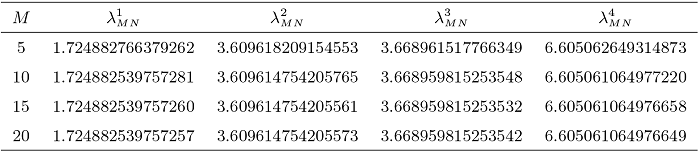
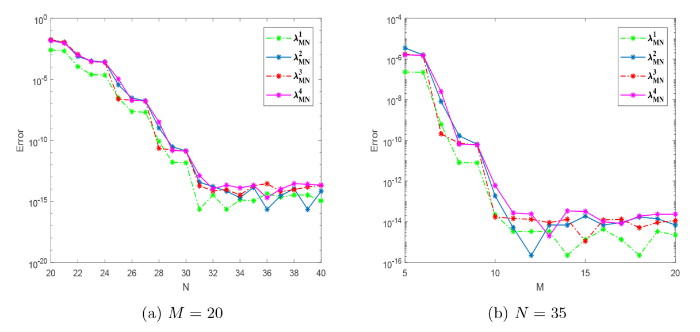
为了表明算法的有效性和谱精度, 我们将进行一系列的数值实验. 我们用$N$表示 Fourier 数值积分节点的个数, 并在 MATLAB R2017a 平台上进行编程计算.

例 5.1 取$\alpha=\beta=1$, 对不同的$N$和$M$, 我们分别在表1和表2中列出了前四个特征值的数值结果.

表1   当$M=5$时, 对于不同的$N$前四个特征值$\lambda_{MN}^i(i=1,2,3,4)$的数值结果

新窗口打开| 下载CSV


表2   当$N=25$, 对于不同的$M$前四个特征值$\lambda_{N}^i(i=1,2,3,4)$的数值结果

新窗口打开| 下载CSV


从表 1 和表 2 可以观察到, 当$N\geq10$,$M\geq10$时前四个不同的特征值达到了至少$14$位有效数字的精度.

例 5.2 取$\alpha=\sin(x+3y)+2$,$\beta={\rm e}^{2\sin(x+y)}$. 对不同的$N$和$M$, 我们分别在表3和表4中列出了前四个特征值的数值结果.

表3   当$M=20$时, 对于不同的$N$前四个特征值$\lambda_{MN}^i(i=1,2,3,4)$的数值结果

新窗口打开| 下载CSV


表4   当$N=35$时, 对于不同的$M$前四个特征值$\lambda_{MN}^i(i=1,2,3,4)$的数值结果

新窗口打开| 下载CSV


从表3-表4可知, 当$M=20$,$N\geq 35$或$N=35$,$M\geq15$时, 前四个不同的特征值都达到了至少$14$位有效数字的精度. 为了进一步表明算法的收敛性和高精度, 我们取$N=45$,$M=25$时的数值解作为参考解, 分别在图1中画出了逼近特征值的误差图像. 从图中可以观察到我们的算法是收敛的和高精度的.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   数值解与参考解之间的误差曲线


6 结论

我们首次提出了周期边界条件下四阶特征值问题一种有效的 Fourier 谱逼近方法, 并从理论上证明了逼近特征值的误差估计. 数值结果表明我们的算法是收敛的和具有谱精度的. 另外, 本文提出的算法还可以应用到一些复杂的非线性问题, 如 KdV 方程、KS 方程和 Allen-Cahn 方程等.

参考文献

An J, Li H Y, Zhang Z M.

Spectral-Galerkin approximation and optimal error estimate for biharmonic eigenvalue problems in circular/spherical/elliptical domains

Numerical Algorithms, 2020, 84(2): 427-455

DOI:10.1007/s11075-019-00760-4      [本文引用: 1]

An J, Luo Z D.

A high accuracy spectral method based on min/max principle for biharmonic eigenvalue problems on a spherical domain

Journal of Mathematical Analysis and Applications, 2016, 439(1): 385-395

DOI:10.1016/j.jmaa.2016.02.048      URL     [本文引用: 1]

An J, Shen J.

A Spectral-Element method for transmission eigenvalue problems

Journal of Scientific Computing, 2013, 57(3): 670-688

DOI:10.1007/s10915-013-9720-1      URL     [本文引用: 1]

An J.

A Legendre-Galerkin spectral approximation and estimation of the index of refraction for transmission eigenvalues

Applied Numerical Mathematics, 2016, 108: 171-184

[本文引用: 1]

BABU Š KA I, Osborn J.

Eigenvalue problems

Handbook of Numerical Analysis, 1991, 2: 641-787

[本文引用: 2]

Banerjee U, Osborn J E.

Estimation of the effect of numerical integration in finite element eigenvalue approximation

Numerische Mathematik, 1989, 56(8): 735-762

DOI:10.1007/BF01405286      URL     [本文引用: 1]

Boffi D.

Finite element approximation of eigenvalue problems

Acta Numerica, 2010, 19: 1-120

DOI:10.1017/S0962492910000012      URL     [本文引用: 1]

We discuss the finite element approximation of eigenvalue problems associated with compact operators. While the main emphasis is on symmetric problems, some comments are present for non-self-adjoint operators as well. The topics covered include standard Galerkin approximations, non-conforming approximations, and approximation of eigenvalue problems in mixed form. Some applications of the theory are presented and, in particular, the approximation of the Maxwell eigenvalue problem is discussed in detail. The final part tries to introduce the reader to the fascinating setting of differential forms and homological techniques with the description of the Hodge–Laplace eigenvalue problem and its mixed equivalent formulations. Several examples and numerical computations complete the paper, ranging from very basic exercises to more significant applications of the developed theory.

Chen L Z, An J, Zhuang Q Q.

Direct solvers for the biharmonic eigenvalue problems using Legendre polynomials

Journal of Scientific Computing, 2017, 70(3): 1030-1041

DOI:10.1007/s10915-016-0277-7      URL     [本文引用: 1]

Chen L Z, Shen J, Xu C J.

A triangular spectral method for the Stokes equations. Numerical Mathematics: Theory

Methods and Applications, 2011, 4(2): 158-179

[本文引用: 1]

Dubiner M.

Spectral methods on triangles and other domains

Journal of Scientific Computing, 1991, 6(4): 345-390

DOI:10.1007/BF01060030      URL     [本文引用: 1]

Fu H F, Rui H X, Hou J, et al.

A stabilized mixed finite element method for elliptic optimal control problems

Journal of Scientific Computing, 2016, 66(3): 968-986

DOI:10.1007/s10915-015-0050-3      URL     [本文引用: 1]

Ge Y X, Tan T, An J.

A high accuracy numerical method and error analysis for fourth order elliptic eigenvalue problems in circular domain

Advances in Applied Mathematics and Mechanics, 2020, 12(3): 815-834

DOI:10.4208/aamm      URL    

Grebenkov D S, Nguyen B T.

Geometrical structure of Laplacian eigenfunctions

SIAM Review, 2013, 55(4): 601-667

DOI:10.1137/120880173      URL     [本文引用: 1]

Griffin A, Snoke D W, Stringari S. Bose-Einstein Condensation. Cambridge University Press, 1996

[本文引用: 1]

Kuttler J R.

A finite-difference approximation for the eigenvalues of the clamped plate

Numerische Mathematik, 1971, 17(3): 230-238

DOI:10.1007/BF01436379      URL     [本文引用: 1]

Lamichhane B P.

A stabilized mixed finite element method for the biharmonic equation based on biorthogonal systems

Journal of Computational and Applied Mathematics, 2011, 235(17): 5188-5197

DOI:10.1016/j.cam.2011.05.005      URL     [本文引用: 1]

Mercier B, Osborn J, Rappaz J, et al.

Eigenvalue approximation by mixed and hybrid methods

Mathematics of Computation, 1981, 36(154): 427-453

DOI:10.1090/mcom/1981-36-154      URL     [本文引用: 1]

Neese F.

Prediction of electron paramagnetic resonance$g$values using coupled perturbed Hartree-Fock and Kohn-Sham theory

Chem Phys, 2001, 115(24): 11080-11096

[本文引用: 1]

Pasquetti R, Rapetti F.

Spectral element methods on unstructured meshes: Comparisons and recent advances

Journal of Scientific Computing, 2006, 27(1): 377-387

DOI:10.1007/s10915-005-9048-6      URL     [本文引用: 1]

Rannacher R.

Nonconforming finite element methods for eigenvalue problems in linear plate theory

Numerische Mathematik, 1979, 33(1): 23-42

DOI:10.1007/BF01396493      URL     [本文引用: 1]

Shen J, Wang L L, Li H Y.

A triangular spectral element method using fully tensorial rational basis functions

SIAM Journal on Numerical Analysis, 2009, 47(3): 1619-1650

DOI:10.1137/070702023      URL    

Sherwin S J, Karniadakis G E.

A triangular spectral element method: Applications to the incompressible Navier-Stokes equations

Computer Methods in Applied Mechanics and Engineering, 1995, 123(1-4): 189-229

DOI:10.1016/0045-7825(94)00745-9      URL     [本文引用: 1]

Tkatchenko A, Scheffler M.

Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data

Physical Review Letters, 2009, 102(7): 073005

DOI:10.1103/PhysRevLett.102.073005      URL     [本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发