量子纠缠是物理学中最基本的概念之一, 在 1935 年, 在文献[1]Schr$\ddot{\mathrm{o}}$dinger 的开创性著作中引入了量子纠缠这个概念. 人们首先在复合系统中发现了一个奇怪的量子现象: 测量其中一个子系统必定会影响其他子系统的量子态. 在 1965 年, 贝尔利用文献[2]的隐变量理论推导出了一个系统的两部分之间的相关性必须满足一个不等式, 即贝尔不等式^[3], 从而将纠缠问题具体化. 随后有学者通过实验发现了量子纠缠的现象. 由于量子纠缠的特性^[4], 量子计算机的功能远远优于目前的经典计算机, 这使我们能够完成经典系统中不可能完成的任务^[5], 如确保通信安全和加速某些困难的计算任务^[6,7]. 因此, 为了更好的利用纠缠这一量子资源, 关于量子纠缠的定量理论便显得尤其重要.

量子纠缠的度量实际上是指一个纠缠态具有多少纠缠量, 它的建立使得不同的纠缠态具有可比性. 近二十年来, 科学家们基本完成了对两体纯态系统纠缠的量化, 但对多体量子系统以及混合态纠缠的定义尚未完成. 现有的纠缠度量包括部分熵^[8]、相对熵^[9]、施密特度量^[10]、纯度度量 (蒸馏纠缠)^[11]、 几何度量^[12] 等, 但是, 这些度量方法并不适用于任意量子态, 有其局限性. 例如部分熵仅适用于两体量子纯态, 而相对熵涉及面广, 但往往难以计算. 因此, 量子纠缠的度量仍值得继续研究. 我们把基于几何意义定义的两体纯态系统$C^{2}\otimes C^{2}$上的纠缠度量的方法扩展到了两体纯态系统$C^{d}\otimes C^{d}$上, 因此, 本文利用向量的楔积的模长得到了两体纯态系统$C^{d}\otimes C^{d}$上的纠缠度量.

本文的结构如下: 在第 2 节中, 首先给出了与本论文的研究内容相关的一些基础知识. 在第 3 节中, 讨论了基于向量楔积的低维两体纯态系统上的纠缠度量. 在第 4 节中, 进一步讨论了基于向量楔积的高维两体纯态系统上的纠缠度量并为可分态提供了一种新的几何判据. 最后, 在第 5 节中进行了总结并提出了未来的研究方向.

为了在两体纯态系统上研究基于向量楔积的纠缠度量, 在本章中列出了一些基础知识, 如楔积的定义、测后向量的定义^[13] 以及纠缠度量的公理化假设^[16] 等.

定义 2.1 设$V$是一个$n$维的线性空间$(n\geq2)$, 具有基$\{\overrightarrow{e_{1}}, \overrightarrow{e_{2}}, \cdots, \overrightarrow{e_{n}}\}$, 又设$\overrightarrow{a_{1}}, \overrightarrow{a_{2}}, \cdots,$$\overrightarrow{a_{m}}$为$V$中的$m$个向量$(m\leq n)$, 它们关于上述基有如下表示

定义

称之为向量$\overrightarrow{a_{1}}, \overrightarrow{a_{2}}, \cdots, \overrightarrow{a_{m}}$的楔积.

首先, 根据定义给出两个向量楔积的定义的几何含义, 以$2$维的线性空间$V$为例来说明它的几何含义,其中$\overrightarrow{a}=a_{1}\overrightarrow{e_{1}}+a_{2}\overrightarrow{e_{2}}$,$\overrightarrow{b}=b_{1}\overrightarrow{e_{1}}+b_{2}\overrightarrow{e_{2}}$,并且

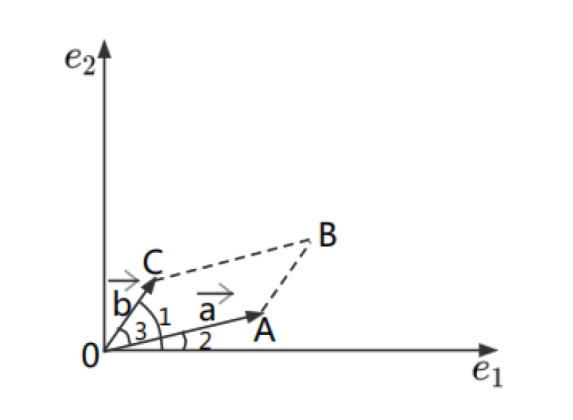
此时, 双矢量$\overrightarrow{a}\wedge\overrightarrow{b}$表示平面上的一个定向平行四边形且$\overrightarrow{a}$和$\overrightarrow{b}$是它的两条邻边,$\overrightarrow{a}$和$\overrightarrow{b}$的楔积的模长的几何表示是一个定向平行四边形的面积.如图1 所示,$S_{OABC}$表示平行四边形$OABC$的面积.

其中$\alpha=\beta-\gamma$,$\sin\beta=\frac{b_{2}}{\sqrt{b_{1}^{2}+b_{2}^{2}}}$,$\sin\gamma=\frac{a_{2}}{\sqrt{a_{1}^{2}+a_{2}^{2}}}$,$(\angle1=\beta, \angle2=\gamma, \angle3=\alpha)$

如果$\overrightarrow{a}$和$\overrightarrow{b}$是平行的, 那么由这两个向量构成的平行四边形的面积等于 0. 要最大化楔积的模长相当于最大化平行四边形的面积,实际上, 对于一定模长的$\overrightarrow{a}$和$\overrightarrow{b}$来说, 当$\overrightarrow{a}$和$\overrightarrow{b}$正交时, 即$\overrightarrow{a}\cdot\overrightarrow{b}=0$, 利用等周定理^[14], 此时, 平行四边形的面积最大. 另外, 当$|\overrightarrow{a}|^{n}+|\overrightarrow{b}|^{n}=c$,$c$是一个常数, 要最大化平行四边形的面积, 需要满足的约束条件为$|\overrightarrow{a}|=|\overrightarrow{b}|$,所以, 当$|\overrightarrow{a}\wedge\overrightarrow{b}|$取得最大值时, 需要满足的约束条件是$\overrightarrow{a}$和$\overrightarrow{b}$相互正交且模长相等, 在几何上对应于$|\overrightarrow{a}|$和$|\overrightarrow{b}|$是线性空间$V$中正方形的边长.

此外, 两个向量的楔积存在 Lagrange-Brahmagupta 恒等式^[15], 其形式为

基于两个向量楔积的定义的几何含义, 进一步给出了三个向量楔积的定义的几何含义, 以$3$维的线性空间$V$为例来说明它的几何含义,其中$\overrightarrow{a}=a_{1}\overrightarrow{e_{1}}+a_{2}\overrightarrow{e_{2}}+a_{3}\overrightarrow{e_{3}}$,$\overrightarrow{b}=b_{1}\overrightarrow{e_{1}}+b_{2}\overrightarrow{e_{2}}+b_{3}\overrightarrow{e_{3}}$,$\overrightarrow{c}=c_{1}\overrightarrow{e_{1}}+c_{2}\overrightarrow{e_{2}}+c_{3}\overrightarrow{e_{3}}$,

此时,$\overrightarrow{a}\wedge\overrightarrow{b}\wedge\overrightarrow{c}$表示欧几里得空间$R^{3}$中的一个定向平行六面体且$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$是它的三条邻边,$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$楔积的模长是平行六面体的体积.通过规定^[13]:$\overrightarrow{e_{1}}\wedge\overrightarrow{e_{2}}=\overrightarrow{e_{3}}$,$\overrightarrow{e_{2}}\wedge\overrightarrow{e_{3}}=\overrightarrow{e_{1}}$,$\overrightarrow{e_{3}}\wedge\overrightarrow{e_{1}}=\overrightarrow{e_{2}}$和$\overrightarrow{e_{1}}\wedge\overrightarrow{e_{2}}=-\overrightarrow{e_{2}}\wedge\overrightarrow{e_{1}}$,$\overrightarrow{e_{1}}\wedge\overrightarrow{e_{1}}=0$, 此时, 平行六面体的体积为

在两个向量以及三个向量楔积的定义的几何含义的基础上, 我们继续给出$n$个向量楔积的定义的几何含义, 目的是利用其几何含义研究高维两体纯态系统$C^{d}\otimes C^{d}$上的纠缠度量. 基于 (2.1) 式, 有

其中$\lambda_{i_{1}i_{2}i_{3}}$是一个常数, 根据行列式的计算,$n$阶行列式可以表示为$n\times(n-1)\times\cdots\times4$个$3$阶行列式之和, 其中$\overrightarrow{a_{i_{ 1}}}, \overrightarrow{a_{i_{2}}}, \overrightarrow{a_{i_{3}}}$分别是这些平行六面体的三条邻边. 此时,$\overrightarrow{a_{1}}, \overrightarrow{a_{2}}, \cdots, \overrightarrow{a_{n}}$的楔积的模长是$d\times(d-1)\times\cdots\times4$个平行六面体的体积.

定义 2.2$N$量子比特系统中的任何态都可以表示为$|\psi\rangle=\sum\limits_{i_{1}, i_{2}, \cdots, i_{N}}C_{i_{1}, i_{2}, \cdots, i_{N}}|i_ {1}\rangle\otimes|i_{2}\rangle\otimes\cdots\otimes|i_{N}\rangle$,其中$C_{i_{1}, i_{2}, \cdots, i_{N}}$是一系列复数且满足归一化条件,$|i_{1}\rangle, |i_{2}\rangle, \cdots, |i_{N}\rangle$分别是子系统$S_{1}, S_{2}, \cdots, S_{N}$中的基，系统$S_{k}$的希尔伯特空间$H_{S_{k}}$是$d_{k}$维,$|\psi\rangle_{S_{1}, S_{2}, \cdots, S_{N}}\in H_{S_{1}}\otimes H_{S_{2}}\otimes\cdots\otimes H_ {S_{N}}$.接下来, 考虑一个双分区$S_{1}\cdots S_{j}|S_{j+1}\cdots S_{N}$,对于子系统$S_{1}\cdots S_{j}$来说, 测后向量^[13] 为$\langle i_{1}\cdots i_{j}|\psi\rangle=\sum\limits_{d_{j+1}, d_{j+2}, \cdots, d_{N}}C_{d_{j+1}, d_{j+2}, \cdots, d_{N}}|d_{j+1}\rangle\otimes |d_{j+2}\rangle\otimes\cdots\otimes|d_{N}\rangle$对应于子系统$S_{j+1}\cdots S_{N}$的希尔伯特空间$H_{S_{j+1}}\otimes\cdots\otimes H_{S_{N}}$且数量为$d_{j+1}\times d_{j+2}\times\cdots\times d_{N}$. 此外,可以利用类似的定义来获得其他子系统的测后向量.

纠缠度量的公理化假设^[16].

最近, 荷兰科学家 Horodecki 等提出了定义纠缠度量的几个公理化假设.

(1) 纠缠度量$E(\rho)$是把密度矩阵$\rho$映射到正实数$R^{+}$的一个映射.

(2) 如果$\rho$是一个可分态, 则$E(\rho)$=0.

(3) (LOCC单调性) 在 LOCC (局部操作和经典通信) 的作用下, 纠缠度不会增加. 也就是说, 对于任何给定的 LOCC$\wedge$:$\rho\mapsto\Sigma_{k}V_{k}\rho V_{k}^{\dagger}$以及$\Sigma_{k}V_{k} V_ {k}^{ \dagger}=I$,$E(\wedge(\rho))\leq E(\rho)$.

(4) (凸性) 纠缠度量$E(\rho)$是一个凸函数,若$\rho=\Sigma_{k}p_{k}\rho_{k}$,$p_{k}\geq0$且$\Sigma_{k}p_{k}=1$, 那么$E(\Sigma_{k}p_{k}\rho_{k})\leq \Sigma_{k}p_{k}E(\rho_{k })$.

当然, 并非所有的纠缠度量都满足这些假设, 事实上, 许多纠缠度量只满足其中一些假设. 此外, 纠缠度量在某些问题中还需要满足一些附加条件, 如可加性、连续性等. 关于在本文中定义的纠缠度量, 我们分别验证了它们确实满足纠缠度量的公理化假设.

定义 3.1 对于任意纯态$|\psi_{AB}\rangle=\alpha|00\rangle+\beta|11\rangle$,$|\alpha|^{2}+|\beta| ^{2}=1$,$|\psi_{AB}\rangle$的纠缠度量的定义为

其中

根据定义, 我们得到两个向量在平面上可以构成一个平行四边形且两个向量的楔积的模长在几何上对应于平行四边形的面积. 当$E$取最大值时, 它在几何上对应于平行四边形的最大面积. 此时, 需要满足的条件是平行四边形的两条邻边相等且相互正交, 即两个向量模长相等且相互正交. 因此, 任意纯态$|\psi_{AB}\rangle$是一个最大纠缠状态, 需要满足条件

此时, 这两个向量是正交的,当$|\alpha|=|\beta|=\frac{\sqrt{2}}{2}$时, 平行四边形的面积最大,$E$取得最大值. 这与$|\psi_{AB}\rangle=\frac{\sqrt{2}}{2}|00\rangle+\frac{\sqrt{2}}{2}|11\rangle$为最大纠缠态这一事实相符.另外, 当任意的纯态$|\psi_{AB}\rangle$是一个可分态时,$|\psi_{AB}\rangle=|\psi_{A}\rangle\otimes|\psi_{B}\rangle$,

此时, 两个向量平行, 即$\langle0_{A}|\psi_{AB}\rangle=k\langle1_{A}|\psi_{AB}\rangle$,这两个向量在平面上不能构成平行四边形, 故这两个向量的楔积的模长在几何上对应的平行四边形的面积等于0. 于是, 任意纯态$|\psi_{AB}\rangle$是可分态, 需要满足的条件是$\langle0_{A}|\psi_{AB}\rangle=k\langle1_{A}|\psi_{AB}\rangle$. 接下来，举一个简单的例子进行说明.

例 3.1 对于一个给定的贝尔态$|\psi_{AB}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$,此时,

且

定义 3.2 对于一个两体量子系统$S$来说, 纯态$|\psi_{AB}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$仅有一个双分区$A|B$, 并发的定义^[17] 为

其中$\rho_{A}=Tr_{B}(\rho)$和$\rho_{B}=Tr_{A}(\rho)$分别是子系统$A$和$B$的约化密度矩阵, 此时,

且$\rho_{A}=Tr_{B}(\rho)=\frac{1}{2}(|0\rangle\langle0|+|1\rangle\langle1|)=\begin{pmatrix} \frac{1}{2} &0\\0&\frac{1}{2}\end{pmatrix}$.

因此,$C=\sqrt{2(1-Tr(\rho_{A}^{2}))}=1$, 当$|\psi_{AB}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$时, 可以得到$C=2E$, 故在两体纯态系统$C^{2}\otimes C^{2}$上定义的纠缠测度$E$是合理的.

基于两体纯态系统$C^{2}\otimes C^{2}$上的度量方法, 在两体纯态系统$C^{3}\otimes C^{3}$上我们进一步定义了$|\varphi_{AB}\rangle$的纠缠度量.

定义 3.3 对于任意纯态$|\varphi_{AB}\rangle=\alpha|00\rangle+\beta|11\rangle+\gamma|22\rangle$,$|\alpha|^{2}+|\beta|^ {2}+|\gamma|^{2}=1$,$|\varphi_{AB}\rangle$的纠缠度量的定义为

其中

根据定义, 我们知道三个向量在欧几里得空间$R^{3}$中可以构成一个平行六面体且三个向量的楔积的模长在几何上对应于平行六面体的体积. 当$E$取最大值时, 它在几何上对应于平行六面体的体积最大, 此时, 需要满足的条件是平行六面体的三条邻边相等且相互正交, 即三个向量模长相等且相互正交. 因此, 任意的纯态$|\varphi_{AB}\rangle$是一个最大纠缠态, 需要满足条件

此时, 这三个向量是正交的, 当$|\alpha|=|\beta|=|\gamma|=\frac{\sqrt{3}}{3}$时, 平行六面体的体积最大,$E$取得最大值.此时, 纯态$|\varphi_{AB}\rangle=\frac{\sqrt{3}}{3}|00\rangle+\frac{\sqrt{3}}{3}|11\rangle+\frac { \sqrt{3}}{3}|22\rangle$是一个最大纠缠态.

接下来, 证明在两体纯态系统$C^{3}\otimes C^{3}$上新定义的纠缠度量$E$满足量子纠缠的公理化假设.

证 (1) 由于$\rho=|\varphi_{AB}\rangle\langle\varphi_{AB}|$, 所以$\rho\mapsto E(\rho)\in R^{+}$, 故$E(\rho)$是将密度矩阵$\rho$映射到正实数$R^{+}$的一个映射.

(2) 当任意纯态$|\varphi_{AB}\rangle$为可分态时,$|\varphi_{AB}\rangle=|\varphi_{A}\rangle\otimes|\varphi_{B}\rangle$,

因此, 当$|\varphi_{AB}\rangle$为可分态时,$E(|\varphi_{AB}\rangle)=0$.此时, 这三个向量相互平行, 即$\langle0_{A}|\varphi_{AB}\rangle=m\langle1_{A}|\varphi_{AB}\rangle=n\langle2_{A}|\varphi_{AB}\rangle$,在欧几里得空间$R^{3}$中不能构成一个平行六面体, 这三个向量的楔积的模长在几何上对应的平行六面体的体积等于0, 所以, 纠缠度量$E (|\varphi_{AB}\rangle)=0$.故任意的纯态$|\varphi_{AB}\rangle$是一个可分态, 需要满足的条件是$\langle0_{A}|\varphi_{AB}\rangle=m\langle1_{A}|\varphi_{AB}\rangle=n\langle2_{A}|\varphi_{AB}\rangle$.

(3) 由于$\rho=|\varphi_{AB}\rangle\langle\varphi_{AB}|$, 所以$\rho\mapsto\Sigma_{k}V_{k}\rho V_{k}^{\dagger}\Rightarrow|\varphi_{AB}\rangle\langle\varphi_{AB}|\mapsto\Sigma_{k}V_{k}|\varphi_{AB}\rangle\langle\varphi_{AB}|V_{k}^{\dagger}$.

其中$|\alpha_{00}|^{2}+|\alpha_{01}|^{2}+|\alpha_{02}|^{2}+|\alpha_{10}|^{2}+|\alpha_{11}|^{2}+|\alpha_{12}|^{2}+|\alpha_{20}|^{2}+|\alpha_{21}|^{2}+|\alpha_{22}|^{2}=1$,此时,

由于在 LOCC 的作用下，行列式的值不变, 因此, 在两体纯态系统$C^{3}\otimes C^{3}$上新定义的纠缠度量$E$是合理的, 故$E$可以作为两体纯态系统$C ^{3}\otimes C^{3}$上的纠缠度量. 证毕.

显然, 这种度量方法计算起来非常方便. 接下来, 将举一个简单的例子来进行说明.

例 3.2 对于一个给定的纯态$|\varphi_{AB}\rangle=\frac{1}{\sqrt{3}}(|00\rangle+|11\rangle+|22\rangle)$,

在低维两体纯态系统中提出的这种度量方法没有涉及任何优化过程, 它满足量子纠缠的公理化假设且可以简单地计算低维两体纯态系统中的纠缠度.

基于两体纯态系统$C^{2}\otimes C^{2}$以及$C^{3}\otimes C^{3}$上的度量方法, 在两体纯态系统$C^{d}\otimes C^{d}$上我们继续定义$|\phi_{AB}\rangle$的纠缠度量.

定义 4.1 对于任意纯态$|\phi_{AB}\rangle= \alpha_{1}|11\rangle+\alpha_{2}|22\rangle+\cdots+\alpha_{d}|dd\rangle, |\alpha_{1 }|^{2}+|\alpha_{2}|^{2}+\cdots+|\alpha_{d}|^{2}=1$,$|\phi_{AB}\rangle$的纠缠度量的定义为

其中

根据定义, 我们知道$d$个向量可以构成$d\times(d-1)\times\cdots\times4$个平行六面体且$d$个向量的楔积的模长在几何上对应于$d\times(d-1)\times\cdots\times4$个平行六面体的体积. 当$E$取最大值时, 它在几何上对应于$d\times(d-1)\times\cdots\times4$个平行六面体的最大体积.此时, 只需让 (4.1) 式取得最大值即可. 当$|\alpha_{1}|=|\alpha_{2}|=\cdots=|\alpha_{d}|=\frac{1}{\sqrt{d}}$,$|\alpha_{1} |^{2}+|\alpha_{2}|^{2}+\cdots+|\alpha_{d}|^{2}=1$时,$|\alpha_{1}||\alpha_{2}| \cdots |\alpha_{d}|$取得最大值, 此时,$d\times(d-1)\times\cdots\times4$个平行六面体的体积最大,$E$取得最大值, 纯态$|\phi_{AB}\rangle=\frac{1}{\sqrt{d}}(|11\rangle+|22\rangle+\cdots+|dd\rangle)$是最大纠缠态.

接下来, 证明在两体纯态系统$C^{d}\otimes C^{d}$上新定义的纠缠度量$E$满足量子纠缠的公理化假设.

证 (1) 由于$\rho=|\phi_{AB}\rangle\langle\phi_{AB}|$, 所以$\rho\mapsto E(\rho)\in R^{+}$, 纠缠度量$E(\rho)$是将密度矩阵$\rho$映射到正实数$R^{+}$的一个映射.

(2) 当任意纯态$|\phi_{AB}\rangle$为可分态时,$|\phi_{AB}\rangle=|\phi_{A}\rangle\otimes|\phi_{B}\rangle$,

因此, 当$|\phi_{AB}\rangle$为可分态时,$E(|\phi_{AB}\rangle)=0$,此时, 这$d$个向量相互平行, 即$\langle1_{A}|\phi_{AB}\rangle=m\langle2_{A}|\phi_{AB}\rangle=\cdots=n\langle d_{A}|\phi_{AB}\rangle$,这$d$个向量不能构成平行六面体且这$d$个向量的楔积的模长在几何上对应的$d\times(d-1)\times\cdots\times4$个平行六面体的体积等于0, 所以, 纠缠度量$E(|\phi_{AB}\rangle)=0$.故任意的纯态$|\phi_{AB}\rangle$是可分态, 需要满足的条件是$\langle0_{A}|\phi_{AB}\rangle=m\langle1_{A}|\phi_{AB}\rangle=\cdots=n\langle d_{A}|\phi_{AB}\rangle$.

(3) 因为$\rho=|\phi_{AB}\rangle\langle\phi_{AB}|$, 所以$\rho\mapsto\Sigma_{k}V_{k}\rho V_{k}^{\dagger}\Rightarrow|\phi_{AB}\rangle\langle\phi_{AB}|\mapsto\Sigma_{k}V_{k}|\phi_{AB}\rangle\langle\phi_{AB}|V_{k}^{\dagger}$.

其中$|\alpha_{11}|^{2}+|\alpha_{12}|^{2}+\cdots+|\alpha_{1d}|^{2}+|\alpha_{21}|^{2 }+|\alpha_{22}|^{2}+\cdots+|\alpha_{2d}|^{2}+\cdots+|\alpha_{d1}|^{2}+|\alpha_{d2}|^{2}+\cdots+|\alpha_{dd}|^{2}=1$,此时,

由于在 LOCC 的作用下, 行列式的值不变, 因此, 在两体纯态系统$C^{d}\otimes C^{d}$上新定义的纠缠测度$E$是合理的, 故$E$可以作为两体纯态系统$C ^{d}\otimes C^{d}$上的纠缠度量. 证毕.

显然, 这种度量方法计算起来非常方便. 接下来, 举一个简单的例子来进行计算.

例 4.1 对于一个给定的纯态$|\phi_{AB}\rangle=\frac{1}{\sqrt{d}}(|11\rangle+|22\rangle+\cdots+|dd\rangle)$,

且

在高维两体纯态系统中提出的这种度量方法不涉及任何优化过程, 它满足量子纠缠的公理化假设且可以简单地计算高维两体纯态系统中的纠缠度.

对于一个量子系统来说, 仅根据可分态和纠缠态的定义很难判断一个态是可分态还是纠缠态, 因此, 我们有必要给出一些判据. 目前, 我们知道有许多可分态的判据, 常见的判据有 PPT 判据^[18] 和 CCNR 判据^[19,20].接下来, 我们分别根据两体纯态系统$C^{2}\otimes C^{2}$,$C^{3}\otimes C^{3}$以及$C^{d}\otimes C^{d}$上向量的楔积的几何含义给出三个新的几何判据.

几何判据 1 对于一个两体纯态系统$C^{2}\otimes C^{2}$, 把纠缠度量$E$定义为 (3.1) 式, 在几何上对应于由 (3.2), (3.3) 式这两个向量作为邻边构成的平行四边形的面积. 若平行四边形的面积为0, 则对应的量子态是可分态.

几何判据 2 对于一个两体纯态系统$C^{3}\otimes C^{3}$, 把纠缠度量$E$定义为 (3.5) 式, 在几何上对应于由 (3.6), (3.7), (3.8) 式这三个向量作为邻边构成的平行六面体的体积. 若平行六面体的体积为0, 则对应的量子态是可分态.

几何判据 3 对于一个两体纯态系统$C^{d}\otimes C^{d}$, 把纠缠度量$E$定义为 (4.1) 式, 在几何上对应于由 (4.2), (4.3),$\cdots$, (4.4) 式这$d$个向量作为邻边构成的$d\times(d-1)\times\cdots\times4$个平行六面体的体积. 若$d\times(d-1)\times\cdots\times4$个平行六面体的体积为 0, 则对应的量子态是可分态.

因此, 可以根据研究问题的需要选择一个简单且合适的几何判据.

首先, 本文基于几何含义给出了向量的楔积的定义以及两体纯态系统$C^{2}\otimes C^{2}$上的纠缠度量$E$. 接下来, 将这种度量方法推广到了两体纯态系统$C^{3}\otimes C^{3}$以及$C^{d}\otimes C^{d}$上并验证了其合理性.

本文研究的量子纠缠度量方法有以下三个创新点: (1) 把纠缠度量$E$定义为向量的楔积的模长与数学上的几何含义相联系来研究量子信息中的纠缠度量问题. (2) 对于两体纯态系统$C^{2}\otimes C^{2}$来说, 定义的纠缠度量$E$和并发在形式上是相关的, 即$C=2E$. (3) 本文的纠缠度量形式简单且直观, 同时满足量子纠缠的公理化假设, 可以用来简单地计算两体纯态系统中的纠缠度.

目前对于两体纯态系统$C^{3}\otimes C^{3}$和$C^{d}\otimes C^{d}$上还没有普遍适用的度量方法, 除了本文的度量方法外, 一些其他的度量方法也被提到, 感兴趣的读者可以做进一步研究. 接下来, 将继续研究$C^{d}\otimes C^{d}$上的纠缠度量, 其中$d$是无限维的, 以及它相应的几何含义.