1 引言
本文在齐次 Robin 边界条件下讨论如下具有捕获项的 Beddington-DeAnglis 型捕食- 食饵模型
其中 \Omega\in \mathrm{R}^{N} (N 表示空间的维数) 是带有光滑边界 \partial\Omega 的有界区域. u 和 v 分别表示食饵和捕食者在 t 时刻的浓度, r 和 k 分别是 u 的最大增长率和环境承载量, a 和 b 分别表示 v 对 u 的饱和作用和 v 之间的相互作用, c 和 d 分别表示 v 对 u 的捕获率和 v 关于 u 的转换率, e_{1}=E_{1}q_{1}, e_{2}=E_{2}q_{2}, 其中E_{1} 和 E_{2} 分别表示人类关于 u 和 v 的捕获能力, q_{1} 和 q_{1} 分别表示相应的捕获系数, d_{1} 和 d_{2} 分别代表u 和 v 的扩散系数, u_{0}(x) 和 v_{0}(x) 都是连续函数. 参数 r,e_{1},e_{2},a,b,c,d,k,d_{1},d_{2},\gamma,\delta 都是正常数. \frac{cv}{1+au+bv} 是 Beddington-DeAnglis (简记为 B-D) 型反应函数. 它与 Holling 型反应函数相比, 分母中多考虑了捕食者间的相互干扰这一项 cv. 虽然比率依赖函数也考虑了捕食者间的相互干扰, 但在低密度情况下的奇异现象常常引起争议. 所以选用 B-D 型反应函数更贴近于实际的生物意义. \frac{\gamma+\delta v}{1+v} 是关于 v 的非常数死亡率, \gamma 为低密度时的死亡率, \delta 为最大死亡率, 其中 \gamma<\delta.
对于模型 (1.1), 当 \gamma=\delta, e_{1}=e_{2}=b=0 时就是常见的具有常数死亡率的 Holling-II 型捕食-食饵扩散模型, 许多学者对此模型进行了研究[1⇓-3]. 如彭锐和史峻平[2] 在 Neumann 边界条件下研究了具有 Holling-II 型捕食-食饵扩散模型稳态解的全局分支解. 当 \gamma=\delta, e_{1}=e_{2}=0 时模型 (1.1) 即为具有 B-D 型反应函数的捕食-食饵模型, 文献 [4,5] 对其以及推广模型进行了深入的研究. 如 Chen 等[4]在 Neumann 边界条件下研究了具有 B-D 型反应函数的捕食-食饵模型常数稳态解的稳定性以及非常数正稳态解的存在性等; Zhao[5]研究了具有 B-D 型反应函数的噪声系统全局正解的存在性, 讨论了噪声对物种灭绝的影响和物种的持久性.
物种的非常数死亡率会随着浓度的增加而变大, 但始终被控制在最大死亡率和最小死亡率之间, 比常数死亡率更贴合实际, 然而目前大多数学者未考虑非常数死亡率对物种的影响. 当 \gamma\neq\delta 时, \frac{\gamma+\delta v}{1+v} 即为非常数死亡率, 文献 [10⇓⇓-13] 对具有非常数死亡率的捕食-食饵模型进行了深入研究. 如 Yang 等[11]研究了具有非常数死亡率的 Holling-III 型捕食-食饵模型平衡点的稳定性和正平衡点的图灵不稳定性; Peng 等[12]研究了具有非常数死亡率的捕食-食饵模型正解的全局存在性、唯一性, 以及物种的持久性和灭绝性.
接下来对模型 (1.1) 作无量纲化处理: 令 \bar{u}=\frac{ru}{k}, \bar{a}=\frac{ak}{r}, \bar{d}=\frac{dk}{r}, 下式中仍用 u, a 和 d 代表示 \bar{u}, \bar{a} 和 \bar{d}. 于是模型 (1.1) 简化为
本文主要研究系统 (1.2) 对应的平衡态系统
正解的存在性、多重性、稳定性和唯一性以及系统 (1.2) 的渐近行为.
这节最后给出一些预备知识.
令 q(x)\in C(\overline{\Omega}), \lambda_{1}(q) 是如下特征值问题的主特征值
则 \lambda_{1}(q) 连续依赖 q, \lambda_{1}(q) 是简单的. 而且, 如果 q_{1}\leq q_{2}, q_{1}\not\equiv q_{2}, 则 \lambda_{1}(q_{1})<\lambda_{1}(q_{2}). 为了简单起见, 记 \lambda_{1}(0) 为 \lambda_{1}, 相应的主特征函数记为 \varphi_{1}.
考虑如下的非线性问题
众所周知, 若 r>d\lambda_{1}, 则方程 (1.4) 存在唯一正解. 记为 \theta_{(\frac{r}{d},\frac{1}{d})}. 特别地, \theta_{(\frac{r}{d},\frac{1}{d})}<r 且 \theta_{(\frac{r}{d},\frac{1}{d})} 连续依赖 r. 显然 \theta_{(\frac{r}{d},\frac{1}{d})}=d\theta_{\frac{r}{d}}.
2 正解的存在性和多重性
本节应用不动点指数理论和稳态分歧理论讨论系统 (1.3) 正解的存在性和多重性. 显然, 当 r>d_{1}\lambda_{1}+e_{1} 时, 系统 (1.3) 存在半平凡解 (d_{1}\theta_{\frac{r-e_{1}}{d_{1}}},0), 记 u^{\ast}=d_{1}\theta_{\frac{r-e_{1}}{d_{1}}}. 首先类似文献 [14, 引理1] 的证明利用特征值的比较原理给出系统 (1.3) 存在正解的必要条件.
引理 2.1 若系统 (1.3) 存在正解, 则
接着运用极值原理以及上下解方法易得系统 (1.3) 正解的先验估计.
引理 2.2 若 d(r-e_{1})>e_{2}(1+a(r-e_{1})), 则系统 (1.3) 的任意正解 (u,v) 满足
其中 Q_{1}=r-e_{1}, Q_{2}=\frac{d(r-e_{1})-e_{2}(1+a(r-e_{1}))}{be_{2}}.
下面为了计算不动点指数, 引入如下记号
定义算子 A_{\nu}:D \rightarrow W 为
其中 \nu\in[0,1], 且 q 是满足 q>\max\{\frac{c}{d_{1}b},\frac{e_{2}+\delta}{d_{2}}\} 的充分大的正常数, 记 A=A_{1}, 显然算子 A 在 D 上的非负不动点即为系统 (1.3) 的非负解. 记 \bar{e}_{2} = -\gamma-d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})}).
注 2.1 由于
从而可知当 r=d_{1}\lambda_{1}+e_{1} 时, \bar{e}_{2}(r)=-\gamma-d_{2}\lambda_{1}<0; 当 r\rightarrow\infty 时, \bar{e}_{2}(r)\rightarrow -\gamma-d_{2}\lambda_{1}+\frac{d}{a}. 由于 \bar{e}_{2}(r) 关于 r 单调递增, 所以当 -\gamma-d_{2}\lambda_{1}+\frac{d}{a}>0 时, 即 d>a(\gamma+d_{2}\lambda_{1}) 时, 必存在唯一的 r^{\ast}>d_{1}\lambda_{1}+e_{1}, 使得 \bar{e}_{2}(r^{\ast})=0. 因此, 当 d>a(\gamma+d_{2}\lambda_{1}) 且 r>r^{\ast} 时 \bar{e}_{2}(r)>0.
引理 2.3 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}. 则
(i) \mathrm{index}_{W}(A,D)=1;
(ii) \mathrm{index}_{W}(A,(0,0))=0;
(iii) 若 e_{2}<\bar{e}_{2}, 则 \mathrm{index}_{W}(A,(u^{\ast},0))=0; 若 e_{2}>\bar{e}_{2}, 则 \mathrm{index}_{W}(A,(u^{\ast},0))=1.
通过引理 2.3 以及度的可加性可得系统 (1.3) 正解存在的充分条件.
定理 2.1 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}. 若 e_{2}<\bar{e}_{2}, 则系统 (1.3) 至少存在一个正解.
证 由度的可加性, 可得
矛盾, 故系统 (1.3) 至少存在一个正解.
接下来, 以 e_{2} 为分歧参数研究系统 (1.3) 在半平凡解 (u^{\ast},0) 处产生的分歧解. 为此引入如下空间
令 \omega = u^{\ast}-u, \chi=v, 则 \omega, \chi \geq0 且满足
其中
令 F(\omega,\chi)=(F_{1}(\omega,\chi),F_{2}(\omega,\chi))^{T}, 显然 F 连续, F(0,0)=0, 且 D_{(\omega,\chi)}F(0,0)=0.
令 K 为 Robin 边界条件下的 (-\Delta)^{-1}, 则问题 (2.1) 等价于
定义 T:\mathrm{R}^{+}\times X\rightarrow X 为
则 T 为 X 上的紧可微算子. 令 G(e_{2};\omega,\chi)=(\omega,\chi)^{T}-T(e_{2};\omega,\chi), 则 G(e_{2};0,0)=0. 显然 G(e_{2};\omega,\chi)=0 当且仅当 (e_{2};u^{\ast}-\omega,\chi) 是系统 (1.3) 的解.
定理 2.2 若 r>d_{1}\lambda_{1}+e_{1}, 则 (e_{2};\omega,\chi)=(\bar{e}_{2};u^{\ast},0) 为系统 (1.3) 的分歧点, 且在 (\bar{e}_{2};u^{\ast},0) 的邻域内, 系统 (1.3) 存在正解 (e_{2}(\epsilon);u(\epsilon),v(\epsilon))=(e_{2}(\epsilon);u^{\ast}-\epsilon(\Phi+\phi(\epsilon)),\epsilon(\Psi+\varphi(\epsilon)))(\epsilon>0), 其中 \Psi 是特征值 \bar{e}_{2} 对应的特征函数, \Phi=(-\Delta-\frac{r-2u^{\ast}-e_{1}}{d_{1}})^{-1}(\frac{cu^{\ast}\Psi}{d_{1}(1+au^{\ast})}), e_{2}(0)=\bar{e}_{2}, \phi(0)=0, \varphi(0)=0.
接着, 将局部分歧延拓为全局分歧. 令 P_{1}=\{u\in C^{1}_{B}(\overline{\Omega}): u>0,x\in\overline{\Omega}\}.
令 e_{2,i}(\mu) 是问题
的特征值, 则 e_{2,1}(1)=\bar{e}_{2}. 类似文献 [19] 的方法可知, 当 e_{2}>\bar{e}_{2} 时, \mathrm{index}(T(e_{2}; \cdot),0)=(-1)^{0}=1, 当 e_{2,2}(1)<e_{2}<\bar{e}_{2} 时, \mathrm{index}(T(e_{2};\cdot))=(-1)^{1}=-1. 故由全局分歧定理[19]可知在 \mathrm{R}^{+}\times X 内, 系统 (1.3) 存在从 (\bar{e}_{2};u^{\ast},0) 出发的连通分支 C, 并且分支 C-\{(\bar{e}_{2};u^{\ast},0)\} 满足下列条件之一
(i) C 连接了分歧点 (\bar{e}_{2};u^{\ast},0) 和 (\hat{e}_{2};u^{\ast},0), 其中 I-T'(\hat{e}_{2}) 不可逆, 且 \bar{e}_{2}\neq\hat{e}_{2};
(ii) C 在 {\mathbb{R}}^{+}\times X 内沿 (\bar{e}_{2};u^{\ast},0) 延伸到 \infty;
(iii) C 包含了形如 (e_{2};u^{\ast}-u,v) 和 (e_{2};u-u^{\ast},-v) 的点, 其中 (u,v)\neq(0,0).
定理 2.3 若 r>d_{1}\lambda_{1}+e_{1}, 则 C-\{(\bar{e}_{2};u^{\ast},0)\} 在正锥 P 内增大到 \infty. 其中 P=\{(e_{2},\omega,\chi)\in {\mathbb{R}}^{+}\times X: \omega,\chi\in P_{1}\}.
证 首先证明 C-\{(\bar{e}_{2};u^{\ast},0)\}\subset P. 假设 C-\{(\bar{e}_{2};u^{\ast},0)\}\nsubseteq P, 则存在点 (\hat{e}_{2};\hat{u},\hat{v})\in C-\{(\bar{e}_{2};u^{\ast},0)\}\cap\partial P 和序列 (e_{2,i};u_{i},v_{i})\subset C\cap P, 使得当 i\rightarrow\infty 时, (e_{2,i};u_{i},v_{i})\rightarrow(\hat{e}_{2};\hat{u},\hat{v}). 显然 \hat{u}\in \partial P_{1} 或 \hat{v}\in\partial P_{1}. 若 \hat{u}\in \partial P_{1}, 则存在 x_{0}\in\overline{\Omega} 使得 \hat{u}(x_{0})=0, 由极值原理可得 \hat{u}(x)\equiv0. 同理 \hat{v}(x)\equiv0. 因此 (\hat{u},\hat{v}) 可能有以下两种情况
(1) 假设 (\hat{u},\hat{v})\equiv(0,0), 则当 i\rightarrow \infty 时, (e_{2,i};u_{i},v_{i})\rightarrow(\hat{e}_{2};0,0). 令 U_{i}=\frac{u_{i}}{\|u_{i}\|_{\infty}}, 则 U_{i} 满足
由 L^{p} 估计和 Sobolev 嵌入定理可知当 i\rightarrow\infty 时, 在 C_{B}^{1}(\bar{\Omega}) 上 U_{i}\rightarrow U 成立, 且 U\geq0,\not\equiv0, 则 U 满足
由极值原理知 U>0, 因此 r=d_{1}\lambda_{1}+e_{1}, 与 r>d_{1}\lambda_{1}+e_{1} 矛盾.
(2) 假设 (\hat{u},\hat{v})\equiv(u^{\ast},0), 则当 i\rightarrow\infty 时, (e_{2,i};u_{i},v_{i})\rightarrow(\hat{e}_{2};u^{\ast},0). 令 V_{i}=\frac{v_{i}}{\|v_{i}\|_{\infty}}, 则 V_{i} 满足
同情况 (1) 有 \hat{e}_{2}=-\gamma-d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})}), 与 \bar{e}_{2}\neq \hat{e}_{2} 矛盾.
因此 C-\{(\bar{e}_{2};u^{\ast},0)\}\subset P, 故全局分歧的条件 (i) 和 (iii) 都不成立, C 只能在 \mathrm{R}^{+}\times X 内沿 (\bar{e}_{2};u^{\ast},0) 延伸到 \infty.
显然正解存在的必要条件 e_{2}<-d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})})\triangleq\Lambda 和充分条件 e_{2}<\bar{e}_{2}=-\gamma-d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})}) 之间存在代沟, 下面对于这个代沟讨论系统 (1.3) 正解的多重性.
定理 2.4 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}, 则存在常数 \hat{e}_{2}\in(\bar{e}_{2},\Lambda), 使得当 e_{2}\in(\bar{e}_{2},\hat{e}_{2}) 时系统 (1.3) 至少有两个正解, 当 e_{2}\leq \bar{e}_{2} 时系统 (1.3) 至少有一个正解.
证 由定理 2.1 可知, 当 e_{2}< \bar{e}_{2} 时系统 (1.3) 至少有一个正解. 故接下来只需证当 e_{2}\in(\bar{e}_{2},\hat{e}_{2}) 时系统 (1.3) 至少有两个正解, 当 e_{2}= \bar{e}_{2} 时系统 (1.3) 至少有一个正解.
取充分大的 M>\max\{\frac{c}{d_{1}b},\frac{e_{2}+\delta}{d_{2}}\}, 定义算子 A_{\kappa}:D\rightarrow W 为
\kappa\in[0,1]. 显然当 \kappa=1 时, 系统 (1.3) 的非负解就是 A_{1} 在 D 上的非负不动点.
设 D_{\epsilon}=\{(u,v)\in W:\parallel(u,v)-(u^{\ast},0)\parallel_{E}<\epsilon\}, 由前文可知e_{2}\in(\bar{e}_{2},\hat{e}_{2}), 存在常数 \epsilon>0, 使得系统 (1.3) 有唯一的正解 (u(\epsilon),v(\epsilon))\in D_{\epsilon}. 因此只需证当 e_{2}\in[\bar{e}_{2},\hat{e}_{2}), 系统 (1.3) 在 D\setminus D_{\epsilon} 上有正解.
令 D_{1}=D\setminus D_{\epsilon}. 由引理 2.2 可知 A_{\kappa} 在 \partial D_{1} 上没有不动点, 从而通过同伦不变性有 \mathrm{index}_{W}(A_{1},D_{1})=\mathrm{index}_{W}(A_{0},D_{1}). 而 A_{0} 在 D_{1} 的不动点只有 (0,0) 和 (u^{\ast},\tilde{v}), 其中 \tilde{v} 是如下问题的唯一正解
由 Dancer 不动点指数定理[16]以及度的可加性有
故 \mathrm{index}_{W}(A_{1},D_{1})=1. 而 \mathrm{index}_{W}(A_{1},(0,0))=0, 故系统 (1.3) 在 D_{1} 内至少有一个正解.
3 正解的唯一性和稳定性
这一节考察当 b 充分大时系统 (1.3) 正解的稳定性和唯一性. 注意到当 b 充分大时, 系统 (1.3) 的正解只有一种类型, 也就是当 b 充分大时系统 (1.3) 的任意正解满足 (u,bv) 趋近于如下问题的正解
如果 r>d_{1}\lambda_{1}+e_{1}, 则问题 (3.1) 等价于
首先给出系统 (3.2) 正解存在且非退化渐近稳定的条件.
引理 3.1 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}. 若 e_{2}<\bar{e}_{2}, 则系统 (3.2) 存在唯一的全局渐近稳定的正解 w^{\ast}.
证 由文献 [19] 中定理 2.1 可知结论显然成立.
引理 3.2 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}, 对任意小的 \sigma, \varepsilon>0, 存在充分大的 M=M(\sigma,\varepsilon)>0, 使得当 b>M 且 e_{2}\in(\varepsilon,\bar{e}_{2}) 时, 系统 (1.3) 的正解 (u,v) 满足 \|u-u^{\ast}\|_{C^{1}_{B}}+\|v\|_{C^{1}_{B}}\leq \sigma, 而且 \|bv-w^{\ast}\|_{C^{1}_{B}}\leq \sigma.
证 反证法. 假设存在 e_{2,i}\rightarrow e_{2}\in[\varepsilon,\bar{e}_{2}], b_{i}\rightarrow\infty, 使得系统 (1.3) 任意正解 (u_{i},v_{i}) 远离 (u^{\ast},0), 在 L^{2} 中 \frac{du_{i}}{1+au_{i}+b_{i}v_{i}}\rightarrow h. 由于 d_{1}\theta_{\frac{r-e_{1}-\frac{c}{b_{i}}}{d_{1}}}\leq u \leq u^{\ast}=d_{1}\theta_{\frac{r-e_{1}}{d_{1}}}. 所以在 C^{1}_{B}(\bar{\Omega}) 中 u_{i}\rightarrow u^{\ast}. 另外由 L^{p} 估计和 Sobolev 嵌入定理可假定 v_{i}\rightarrow v. 则
由于 v\geq0, 所以考虑如下两种情况
(i) 若 v\equiv 0, 则 (u_{i},v_{i})\rightarrow (u^{\ast},0), 与假设矛盾;
(ii) 若 v\geq0,\not\equiv 0, 由 Harnack 不等式得 v>0, 则 h=0, 于是由 (3.3) 式可知 v\equiv 0, 矛盾. 故 \|u-u^{\ast}\|_{C^{1}_{B}}+\|v\|_{C^{1}_{B}}\leq \sigma.
接下来证明 b_{i}\|v_{i}\|_{\infty} 是一致有界的. 反证法, 假设 b_{i}\|v_{i}\|_{\infty}\rightarrow\infty. 令 \tilde{v}_{i}=\frac{v_{i}}{\|v_{i}\|_{\infty}}, 则
同上由正则性理论假设在 C^{1}_{B} 中 \tilde{v}_{i}\rightarrow \tilde{v}\geq0,\not\equiv0. 对 (3.4) 式取极限可得
由 Harnack 不等式得 \tilde{v}>0, 而由上式得 \tilde{v}\equiv0, 矛盾. 故 b_{i}\|v_{i}\|_{\infty} 一致有界.
设 b_{i}v_{i}=w_{i}, 则\|w_{i}\|_{\infty} 一致有界, 且 w_{i} 满足
由正则性理论可假定在 C^{1}_{B} 中 w_{i}\rightarrow w. 对 (3.5) 式取极限, 显然 w 是系统 (3.2) 的非负解.
(i) 当 e_{2}=\bar{e}_{2} 时由文献 [21, 定理 2.1] 可知系统 (3.2) 只有零解, 即 b_{i}v_{i}=w_{i}\rightarrow w=0;
(ii) 当 e_{2}\in(\varepsilon,\bar{e}_{2}) 时, 由引理 3.1 可知 b_{i}v_{i}=w_{i}\rightarrow w=w^{\ast}.
最后, 给出系统 (1.3) 正解的稳定性和唯一性条件.
定理 3.1 设 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}, 对任意小的 \varepsilon>0, 存在充分大的 M(\varepsilon), 使得当 b>M(\varepsilon), e_{2}\in(\varepsilon,\bar{e}_{2}) 时, 系统 (1.3) 存在唯一正解且非退化线性稳定.
证 用反证法. 设 (u,v) 是系统 (1.3) 的正解, \tau=\frac{1}{b}, w=bv, 考虑如下问题
假设 b_{i}\to\infty,e_{2,i}\to e_{2}\in[\varepsilon,\bar{e}_{2}] 时, 系统 (3.6) 存在退化或线性不稳定的正解 (u_{i},w_{i}), 即系统 (3.6) 在 (u_{i},w_{i}) 处的线性化特征值问题存在 \mathrm{Re}(\mu_{i})\leq0 的特征值 \mu_{i}, 以及满足 \|\xi_{i}\|_{L^{2}}^{2}+\|\eta_{i}\|_{L^{2}}^{2}=1 的特征函数 (\xi_{i},\eta_{i})\not\neq(0,0), 使得
由 L^{p} 估计可知 u_{i},w_{i}\in W^{2,p} 且有界, 因此 \{\mathrm{Im}(\mu_{i})\} 和 \{\mathrm{Re}(\mu_{i})\} 有界, 即 {\mu_{i}} 有界, 假设 \mu_{i}\to\mu, 则 \mathrm{Re}(\mu)\leq0. 同理由 L^{p} 估计可知 \|\xi_{i}\|_{W^{2,2}},\|\eta_{i}\|_{W^{2,2}} 有界, 所以假设在 H^{1} 中 \xi_{i}\to \xi,\eta_{i}\to\eta. 结合引理 3.2 对系统 (3.7) 取极限得
若 \xi\not\equiv0, 则 \mu\geq\lambda_{1}(-\frac{r-2u^{\ast}-e_{1}}{d_{1}})>\lambda_{1}(-\frac{r-u^{\ast}-e_{1}}{d_{1}})=0, 矛盾, 故 \xi\equiv0. 同理 \eta\equiv0, 矛盾. 故当 b_{i}\to\infty 时, 系统 (1.3) 的任意正解非退化且线性稳定.
最后证明系统 (1.3) 正解的唯一性. 由已知条件可得系统 (1.3) 存在正解. 根据算子 A 的紧性理论可知系统 (1.3) 至多有有限个正解, 记为 \{(u_{i},v_{i}):1\leq i\leq n\}. 而 \overline{W}_{(u_{i},v_{i})}=S_{(u_{i},v_{i})}, 所以 A'(u_{i},v_{i}) 在 \overline{W}_{(u_{i},v_{i})} 上没有 \alpha 性质, 又因为系统 (1.3) 任意正解非退化且线性稳定, 于是根据文献 [16] 可知 \mathrm{index}_{W}(A,(u_{i},v_{i}))=1. 结合引理 2.3 和度的可加性可得 1=\mathrm{index}_{W}(A,D)=0+\sum_{1\leq i\leq n}\mathrm{index}_{W}(A,(u_{i},v_{i}))=n.
即系统 (1.3) 正解唯一.
4 渐近行为
首先, 运用抛物系统的比较原理易得两物种灭绝的条件, 由于证明方法基础, 故在此省略.
定理 4.1 (i) 若 r\leq d_{1}\lambda_{1}+e_{1}, 则当 t\to\infty 时, 系统 (1.2) 的正解 (u,v)\to (0,0);
(ii) 若 d>a(\gamma+d_{2}\lambda_{1}), r>r^{\ast}, e_{2}>\bar{e}_{2}, 则当 t\to\infty 时, 系统 (1.2) 的正解 (u,v)\to(u^{\ast},0).
引入如下假设
设 d>a(\delta+d_{2}\lambda_{1}), r>r^{\ast} 且 (4.1) 式成立, 则如下问题
分别存在唯一正解, 记作 u_{\ast}, v^{\ast} 和 v_{\ast}, 且 u_{\ast}\leq u\leq u^{\ast}, v_{\ast}\leq v\leq v^{\ast}.
定理 4.2 设 d>a(\delta+d_{2}\lambda_{1}), r>r^{\ast} 且 (4.1) 成立, 则在 C^{1}(\bar{\Omega})\cap C^{2}(\bar{\Omega}) 存在函数 (\underline{u},\underline{v}) 和 (\bar{u},\bar{v}) 满足
和如下关系
进一步, [\underline{u},\bar{u}]\times[\underline{v},\bar{v}] 是系统 (1.2) 的正全局吸引子.
证 令 (f(u,v),g(u,v))=(\frac{u}{d_{1}}(r-u-e_{1}-\frac{cv}{1+au+bv}),\frac{v}{d_{2}}(\frac{du}{1+au+bv}-\frac{\gamma+\delta v}{1+v}-e_{2})). 首先由上下解方法易证 (u^{\ast},v^{\ast}) 和 (u_{\ast},v_{\ast}) 是系统 (1.3) 的一对上下解, 显然 (f,g) 是混拟单调函数且满足 Lipschitz 条件, 于是由单调迭代序列方法可知存在满足上述条件的一对函数 (\underline{u},\underline{v}) 和 (\bar{u},\bar{v}).
下证正全局吸引子成立. 由于系统 (1.2) 的非负解 u 满足下式
而 r>d_{1}\lambda_{1}+e_{1}, 由比较原理
则对任意充分小的 \epsilon>0, 存在 T(\epsilon)>0, 使得对所有的 t>T(\epsilon), 都有 u(x,t)\leq u^{\ast}+\epsilon. 将其代入系统 (1.2) 的第二个式子, 得
由比较原理可得
故存在 T^{'}(\epsilon)>0, 使得对所有的 t>T^{'}(\epsilon), 都有 v(x,t)\leq v^{\ast}+\epsilon.
另一方面, 由于
由比较原理有
则存在 T^{''}(\epsilon)>0, 使得对所有的 t>T^{''}(\epsilon), 都有 u(x,t)\geq u_{\ast}-\epsilon. 将其代入系统 (1.2) 的第二个式子, 得
再由比较原理可知
则存在 T^{'''}(\epsilon)>0, 使得对所有的 t>T^{'''}(\epsilon), 都有 v(x,t)\geq v_{\ast}-\epsilon.
令 T=\max\{T(\epsilon),T^{'}(\epsilon),T^{''}(\epsilon),T^{'''}(\epsilon)\}, 由 (4.2)-(4.5) 式, 对所有的 t>T 和任意的 \epsilon>0 有
令 \epsilon\to 0 并结合文献 [22, 推论 2.1 和定理 2.1] 得出结论. 定理 4.2 得证.
5 数值模拟
本节通过数值模拟对理论结果进行补充和说明. 采用 Matlab 软件及有限差分法在一维情形 \Omega=(0,l) 下模拟系统 (1.2). 用二阶中心差分格式离散空间变量 x, Crank-Nicholson 近似时间变量 t.
首先给出判别 e_{2}<\bar{e}_{2}=-d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})})-\gamma 的条件. 因为 \lambda_{1}(-\frac{d\theta_{r-e_{1}}}{d_{2}(1+a\theta_{r-e_{1}})})<\lambda_{1}-\frac{d(r-e_{1}-\lambda_{1})}{d_{2}(1+a(r-e_{1}))}, 所以 -d_{2}\lambda_{1}(-\frac{du^{\ast}}{d_{2}(1+au^{\ast})})-\gamma>-d_{2}\lambda_{1}(-\frac{d\theta_{r-e_{1}}}{d_{2}(1+a\theta_{r-e_{1}})})-\gamma >-d_{2}\lambda_{1}+\frac{d(r-e_{1}-\lambda_{1})}{1+a(r-e_{1})}-\gamma\doteq\bar{B}. 因此, 如果 e_{2}<\bar{B}, 则 e_{2}<\bar{e}_{2}.
图1
图2
图2
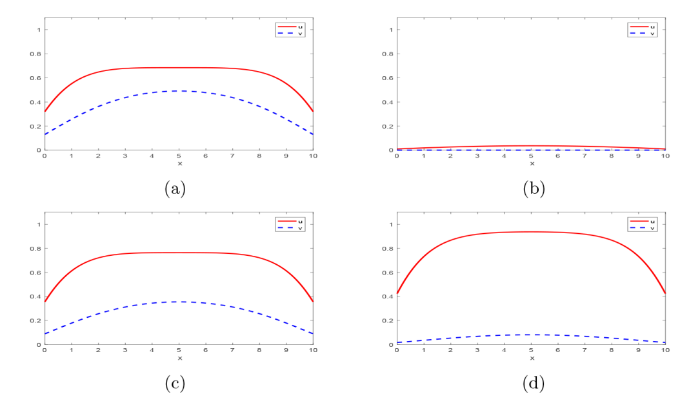
参数 e_{1} 和 e_{2} 的影响. 图(a) 和 (b): e_{1}=0.2,e_{1}=1.1; 图(c) 和 (d): e_{2}=0.25,e_{2}=0.48
图3
图3
参数 d_{1} 和 d_{2} 的影响. 图(a) 和 (b): d_{1}=0.1,d_{1}=1.5; 图(c) 和 (d): d_{2}=0.1,d_{2}=1.5
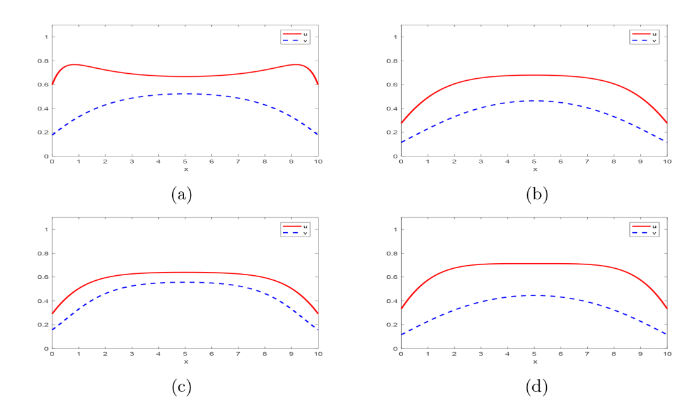
(4) 非常数死亡率的影响. 为了刻画非常数死亡率的影响, 参数 \gamma 和 \delta 的取值见图4, 其余参数同 (1), 易验证定理 4.2 的条件成立. 数值模拟显示随着 \gamma 和 \delta 的增大, 捕食者 v 的浓度减小, 食饵 u 的浓度增大, 这与实际情况相符, 见图4(a), (b), (c) 和 (d). 当 \gamma=\delta=0.1,0.6 时即为常数死亡率, 仍有相同的结果, 可见图4(e) 和 (f). 此外, 观察图4(d) 和 (f) 发现: 当非常数死亡率的最大死亡率取 0.9 时仍可以保证两物种的共存, 而当常数死亡率取 0.6 时捕食者浓度趋于0, 即两物种不共存, 这与实际情况和定理 4.2 的结论均不符. 因此非常数死亡率更适用于模拟物种动力学行为.
图4
图4
参数 \gamma 和 \delta 的影响. 图(a) 和图(b): \gamma=0.1,\gamma=0.3; 图(c) 和图(d): \delta=0.5,\delta=0.9; 图(e)和图(f): \gamma=\delta=0.1, \gamma=\delta=0.6
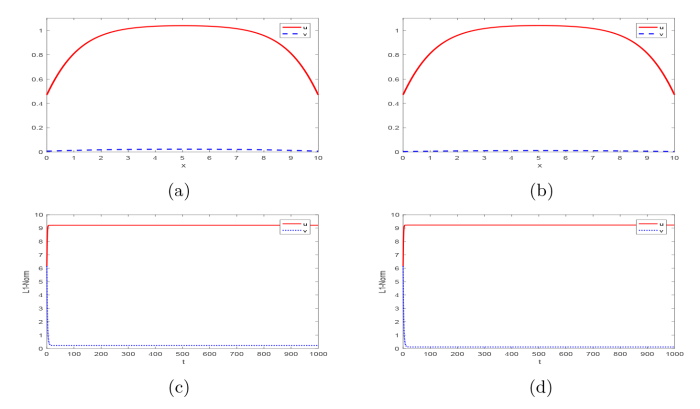
(5) 捕食者间的相互作用 b 的影响. 固定其它参数 r=1.2,e_{1}=0.15,e_{2}=0.15, \gamma=0.2, \delta=0.6, a=1.2,c=1.4,d=5.4,d_{1}=1,d_{2}=1, 结合数值模拟验证了当食饵的增长率 r 和捕食者的捕获率 e_{2} 满足一定条件时, 对于充分大的 b, 系统 1.2 的平衡态正解趋于 (u^{*},0), 见图5(a) 和 (b). 并且正解稳定, 见图5(e) 和 (f), 这与定理 3.1 吻合. 此外, 由图可知捕食者间的相互作用 b 越强, 捕食者 v 的浓度会减少, 而食饵 u 的浓度会增大, 这与实际情况相符.
图5
6 结论
本文在 Robin 边界条件下研究了一类具有捕获项的 B-D 型捕食-食饵扩散模型, 与具有 Holling 型反应函数的捕食-食饵模型相比, B-D 型反应函数的引入丰富了动力学行为的研究. 通过分析得到: 当食饵的增长率较大且捕食者的捕获率和低密度死亡率较小即 r>r^{\ast}>d_{1}\lambda_{1}+e_{1}, e_{2}<\bar{e}_{2}且 d>a(\gamma+d_{2}\lambda_{1}) 时两物种能够共存; 当食饵的增长率过小或捕食者的捕获率较大时, 两物种将灭绝; 进而当捕食者间的相互作用 b 非常大时, 系统 (1.3) 存在唯一且渐近稳定的正解; 而当捕食者的捕获率 e_{2}\in(\bar{e}_{2},\hat{e}_{2}) 时系统 (1.3) 至少存在两个正解. 研究结果表明人类捕获率越大, 两物种的数量会快速减少并最终灭绝, 所以为了保护物种的多样性, 采取适当的捕捞策略是很有必要的; 此外, 与常数死亡率相比, 具有非常数死亡率的生物模型更贴合实际.
参考文献
Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge
DOI:10.1016/j.jde.2006.08.001 URL [本文引用: 1]
Non-existence of non-constant positive steady states of two Holling type-II predator-prey systems: Strong interaction case
DOI:10.1016/j.jde.2009.03.008 URL [本文引用: 2]
Global analysis in Bazykin's model with Holling II functional response and predator competition
DOI:10.1016/j.jde.2021.01.025 URL [本文引用: 1]
Qualitative analysis of predator-prey models with Beddington-DeAngelis functional response and diffusion
DOI:10.1016/j.mcm.2005.05.013 URL [本文引用: 2]
Analysis on stochastic dynamics of two-consumers-one-resource competing systems with Beddington-DeAngelis functional response
DOI:10.1142/S1793524520500588
URL
[本文引用: 2]

In this paper, stochastic dynamics with Lévy noise of two-consumers-one-resource competing systems with Beddington–DeAngelis functional response are considered. We first show the existence of the global positive solution, then discuss the effects of noises on the extinction of the species and the stochastic persistence of the species. In the meanwhile, numerical simulations are carried to support results. Finally, we show the existence of the stationary distribution for a special case.
Analysis on bifurcation for a predator-prey model with Beddington-DeAngelis functional response and non-selective harvesting
DOI:10.1007/s10440-015-0025-2 URL [本文引用: 2]
The dynamics of a harvested predator-prey system with Holling type IV functional response
Analysis of optimal harvesting of a predator-prey model with Holling type IV functional response
DOI:10.1016/j.ecocom.2020.100816 URL [本文引用: 2]
Pattern formations of a delayed diffusive predator-prey model with predator harvesting and prey social behavior
DOI:10.1002/mma.v44.11 URL [本文引用: 1]
On the dynamics of a predator-prey model with nonconstant death rate and diffusion
DOI:10.1016/j.nonrwa.2011.01.002 URL [本文引用: 1]
Bifurcation analysis of a diffusive predator-prey system with nonconstant death rate and Holling III functional response
DOI:10.1016/j.chaos.2014.10.011 URL [本文引用: 2]
The dynamics of stochastic predator-prey models with non-constant mortality rate and general nonlinear functional response
Dynamics of a predator-prey model with strong Allee effect and nonconstant mortality rate
DOI:10.3934/mbe.2022157
PMID:35341257
[本文引用: 1]

In this paper, dynamics analysis for a predator-prey model with strong Allee effect and nonconstant mortality rate are taken into account. We systematically studied the existence and stability of the equilibria, and detailedly analyzed various bifurcations, including transcritical, saddle-node, Hopf and Bogdanov-Takens bifurcation. In addition, the theoretical results are verified by numerical simulations. The results indicate that when the mortality is large, the nonconstant death rate can be approximated to a constant value. However, it cannot be considered constant under small mortality rate conditions. Unlike the extinction of species for the constant mortality, the nonconstant mortality may result in the coexistence of prey and predator for the predator-prey model with Allee effect.
一类食物链模型正解的稳定性和唯一性
Stability and uniqueness of positive solutions for a food-chain model
Existence and asymptotic behavior of positive solutions for a one-prey and two-competing-predators system with diffusion
DOI:10.1016/j.nonrwa.2015.07.010 URL [本文引用: 1]
On the indices of fixed points of mappings in cones and applications
DOI:10.1016/0022-247X(83)90098-7 URL [本文引用: 3]
The coexistence states of a predator-prey model with nonmonotonic functional response and diffusion
DOI:10.1007/s10440-008-9319-y URL [本文引用: 1]
Bifurcation from simple eigenvalues
DOI:10.1016/0022-1236(71)90015-2 URL [本文引用: 1]
Global bifurcation of coexistence state for a competition model in the chemostat
DOI:10.1016/S0362-546X(98)00250-8 URL [本文引用: 3]
Some global results for nonlinear eigenvalue problems
DOI:10.1016/0022-1236(71)90030-9 URL
Existence and structure of the set of positive solutions of a general class of sublinear elliptic non-classical mixed boundary value problems
DOI:10.1016/S0362-546X(01)00116-X URL [本文引用: 1]
Quasisolutions and global attractor of reaction-diffusion systems
DOI:10.1016/0362-546X(95)00058-4 URL [本文引用: 1]