如何描述一个随机系统 (过程) 的平稳程度是一个重要的研究课题. 如果刻画它的统计性质不随时间变化, 该系统被称为是平稳的, 否则就称为是非平稳的^[1]. 而时间序列被研究的最多, 序列之间通常存在相关性, 在一定程度上可以反映系统的某些规律, 这就启发了我们利用现有的观测结果来预测以后可能会发生的事. 评价一个时间序列是否平稳, 主要是看其均值和方差是否随时间变化, 自相关函数是否只与时间间隔有关^[2]. 对于一般数据, 常见的平稳性测试方法有游程检验法、逆序检验法、特征根测试以及参数测试方法等许多方法^[3].

在非线性时间序列的分析中, 由于时间序列动态非平稳性的存在, 一些分析结果的可靠性不是很高, 因此我们需要对非平稳性度量展开深入的研究. 在计量经济学方面, 非平稳性度量研究主要集中在时间序列的单位根检验方面^[4]. 客观上来说, 非平稳性的问题存在于任何有序的数据生成过程 (Data Generating Process, DGP) 中, 可以将数据流看作广义上的时间序列, 来探究其平稳程度. 在动力系统领域中是将 DGP 数据假设为确定性动力系统. 但是我们并不能对数据生成过程做太多设定, 需要寻求一种比较通用的度量非平稳性的方法.

非平稳性度量指标 NS 的引入可以很好的解决这个问题. 最初的想法是借助遍历论、粗粒化方法对数据流的非平稳程度进行研究^[5], 引入非平稳性度量的概念. 已经证实该指标在很多领域都有着广泛的应用, 针对时间序列我们可以用 NS 量化序列的非平稳性. 在非平稳性度量研究中最重要的是稳定集合判别标准的选取, 一个好的稳定集合判别标准能帮助我们更好的寻找稳定集合, 现有的判别标准得到的非平稳性度量已经趋于成熟并得到广泛应用^[6], 一个典型的应用就是模型选择. 对模型的残差序列进行平稳性分析可以更好的反映模型的正确性, 当残差序列不够平稳时, 可以认为序列中还存在某种趋势信号, 模型存在偏差^[7,8]. 需要在多个预先给定的模型中选出一个最符合数据生成过程的模型. 这个时候对残差序列的平稳程度的估计就显得尤为重要, 需要比较两个序列的平稳程度, 然而当两个序列均比较平稳, 现有的判别标准对其区分度不够. 这就意味着对于那些稳定程度较高且非常接近的序列, 需要找寻一个更为严格的判别标准, 使得在同样条件下, 新标准能够区分一些在原有标准下稳定性相近的集合, 提高在 NS 较小时的分辨率.

重对数律本质上是一种偏差不等式, 是对随机变量和的一种估计, 可以用来对频率序列的收敛程度进行估计, 并且所得到的界是可信的. 中心极限定理是对独立随机变量和偏离其均值的一种估计, 所以我们将尝试其他的偏差不等式如 Hoeffding 不等式、Bennett 不等式、以及重对数律来构建新的判别标准, 并与中心极限定理进行比较. 希望对频率序列进行更精确的估计, 以此来控制频率序列的收敛速度, 以便能够更好的区分那些稳定程度相近的序列. 本文利用重对数律构建新的非平稳性度量, 所得到的新判别标准相较之前更加严格, 对模型的稳定性要求更高. 对非确定性信号, 新标准对一阶自回归模型的收敛要求更高, 计算得到的 NS 值也越大. 在确定性信号方面, 新方法在参数校准上的优势则更加明显, 得到的参数值比原有标准更加精确, 相对误差更低. 一个更严格的稳定集合判别标准有着重要的意义, 使得在某些对精度要求更高的场景下能够对序列进行更好的判别, 实现了对精度的更进一步提高.

本文在第二节介绍非平稳性度量相关理论, 第三节介绍各类偏差不等式, 第四节将构建的新判别标准与原有的进行比较, 最后总结全文.

本节介绍刻画非平稳性度量指标(NS)的基本思想和近似计算过程.

为了定义非平稳性度量, 首先给出稳定集合的定义. 设 $X=\left\{x_{n}\right\}_{n=1}^{\infty} \subseteq \Omega:=[0,1], \mathbb{A}=\left\{A_{1}, A_{2}, \cdots, A_{m}\right\}$ 称为 $\Omega$ 的一个划分, 如果 $A_{i} \cap A_{j}=\emptyset\ (i \neq j)$, 且 $\bigcup\limits_{i=1}^{m} A_{j}=\Omega$. 若 $A \subset \Omega$, $I_{A}(x)$ 表示集合 $A$ 的示性函数, $I_{A}(x) = 1$ 当且仅当 $x \in A$.

定义 2.1^[4] $A \subseteq \Omega$ 称为 $X$ 的稳定集合, 如果 $X$ 中的点进入 $A$ 的频率序列

收敛，且极限为常数 $P_X(A)$.

定义 2.1 对稳定集合的定义是个极限 (无限) 意义下的概念, 而通常在实际数据分析过程当中, 数据长度往往是有限的. 如何化解这种事实上的“有限”和理论上的“无限”的矛盾, 需要引入稳定集合的判别标准. 好的稳定集合判别标准得到的稳定集合更为准确, 从最开始提出的三角形区域判别改进到梯形区域判别^[1], 后面利用中心极限定理对频率序列收敛程度的控制, 提出了判别更为准确的基于中心极限定理的稳定集合判别标准^[4].

定义 2.2^[4] 给定有限时间序列样本

及样本 $X_L$ 掉到集合 $A$ 的概率为 $f$, 已知集合 $A \subseteq \Omega$, 依 (2.1) 式产生频率序列$\left\{f_{k}(A)\right\}_{k=1}^{L}$, 给定 $\lambda$, 定义区间序列

及

设定阈值 $p_0$, 若 $P_{C, A}(\lambda, f) \geq p_{0}$, 则称集合 $A$ 为 $X_L$ 的稳定集合, 该稳定集合判别标准记为 $C(\lambda, p_0)$.

有了初始划分 $\mathbb{A}=\{A_{1}, A_{2}, \cdots, A_{m}\}$ 和稳定集合判别标准 $C(\lambda, p_0)$, 我们可以寻找稳定集合. 利用粗粒化的思想, 对划分中同一个小区间 $A_i$ 中的点不作区分, 这样只需检查有限个区间, 稳定集合越多, 系统越平稳.

定义 2.3^[1] 给定初始划分 $\mathbb{A}=\{A_{1}, A_{2}, \cdots, A_{m}\}$, 如果每个 $A_i$ 在稳定标准 $C(\lambda, p_0)$ 下都是稳定集合, 则 $\mathbb{A}$ 称为 $X$ 的以 $C(\lambda, p_0)$ 为标准的稳定划分. 三元组 $(\Omega, \mathcal{A}, P)$ 称为 $(X, C)$ 的一个信息结构, 其中 $P(A) = P_X(A)$.

有限样本条件下, 文献 [4] 提出了二叉树算法、从左到右稳定区间搜索算法等四种稳定信息结构提取算法. 有了稳定集合定义、稳定集合判别标准、稳定信息结构的定义及其获取算法, 下面给出非平稳性度量的定义.

定义 2.4^[4] 给定判别标准 $C$ 和初始划分 $\mathbb{A}$, 用 $\mathcal{A}$ 表示由 $\mathbb{A}$ 生成的 $\sigma$ 代数. $\sigma (\mathbb{A})$ 的稳定子 $\sigma $-代数信息熵的最大值定义为序列 $X$ 的信息熵^[9], 即

其中 $\mathfrak{A}_X$ 为 $(X,C)$ 的一个集合包含于 $\mathcal{A}$ 的全部稳定信息结构. $X$ 的非平稳性度量定义为

其中 $H(\mathbb{A})$ 为初始划分 $\mathbb{A}$ 的信息熵, $X$ 的非平稳性度量简记为 $NS$.

(1) (2.5) 式中的上确界是可以达到的, 因为初始划分所产生的 $\sigma $-代数仅包含有限个集合, 它的子 $\sigma $-代数只有有限个.

(2) (2.5) 式中熵 $H(F)$ 的最大值不超过 $H(\mathbb{A})$. $NS_{\mathbb{A}, C}(X)$ 越小, 时间序列的平稳性越好; 反之, $NS_{\mathbb{A}, C}(X)$ 越大, 时间序列的平稳性越差.

在初始划分方式与稳定标准给定的情况下, $NS$ 取决于稳定信息结构获取算法, 其计算流程大体为: 首先输入数据流 $X$, 然后获取稳定信息结构 $SIS$, 最后计算得到 $NS$.

前面定义了非平稳性度量指标 NS, 如何验证这个非平稳性度量指标是否合理? 非平稳性度量指标若被认为是合理的, 如果它满足^[10,11]

(1) 数据是独立同分布 (i.i.d), 则 $NS \rightarrow 0$;

(2) 数据有较强趋势, 则 $NS \rightarrow 1$;

(3) 数据满足一阶自回归模型 $AR(1)$

有如下不等式成立

下面重点对非平稳性度量指标条件第三条进行验证, 在参数 $\rho \rightarrow 0$ 时, 模型 $AR(1)$ 中噪声占主导, 此时序列接近于 i.i.d, 又因为 $NS$ 的计算依赖于随机样本及相关参数, 所以需要在同一 $\rho$ 下取多组样本, 分别计算 $NS$ 再取平均, 期望得到不等式关系

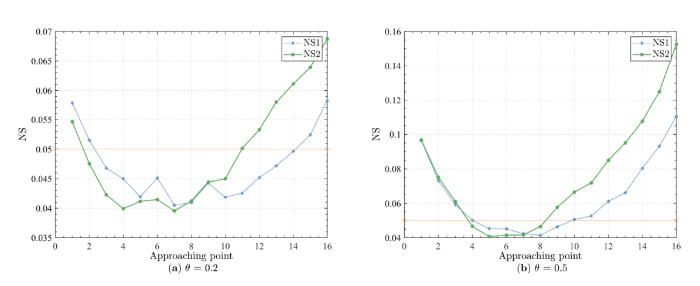
实验参数设置: $L=1000, S=200$. $NS$ 设置: 等分位数下划分$N=\left[1.87(L-1)^{0.4}\right\rfloor, $ $\lambda=1.96, P_{0}=0.92$, 实验结果如图1.

可以看出, 随着 $\rho$ 从 0 增大到 1, 非平稳性度量指标 $NS$ 从 0 (或接近于 0) 单调增大至 1 (或接近 1). 但在 $\rho \in (0,0.5)$ 时, $NS$ 的值均比较小. 也就是说在 $NS$ 值比较小时, 对稳定集合的分辨率较小. 虽然可以通过调节参数 $\lambda$ 方法来控制该判别标准的尺度, 但其精度终归是有限的, 这可能是由中心极限定理的性质所决定, 这就启发我们寻找一种更为严格的判别标准, 使得在 $\rho$ 较小时 $NS$ 的值更大一点.

中心极限定理说明, 在许多情况下, 添加独立随机变量时, 即使原始变量本身未呈正态分布, 其适当归一化的和仍趋于正态分布, 该定理可以借助正态分布来对随机变量偏离其均值的程度作估计^[12]. 而在概率论中, 偏差不等式为随机变量如何偏离某个值(通常是其期望值)提供了界限. 可以根据需要使用多少有关随机变量的信息来对偏差不等式进行分类^[13].

(1) 马尔科夫不等式 (Markov's inequality)

令 $X$ 是一个非负的随机变量, 对于每个常数 $a>0$

(2) 切比雪夫不等式 (Chebyshev's inequality)

切比雪夫不等式要求随机变量 $X$ 满足: 期望 $E[X]$ 与方差 $Var[X]=E[(X-E[X])^2]$ 有限. 对于每个常数 $a>0$ 有

(3) 切尔诺夫界 (Chernoff bound)

通用的 Chernoff 边界仅需要 $X$ 的时刻生成函数, 如果它存在就可以定义为: $M_{X}(t):=E\left[{\rm e}^{t X}\right]$. 基于马尔科夫不等式, 对每个 $t>0$

对每个 $t<0$

(4) 独立随机变量和的界 (Bounds on sums of independent variables)

令 $X_1,X_2,\cdots, X_n$ 是独立的随机变量, 对于所有的 $i: a_i \leq X_i \leq b_i, c_i:=b_i-a_i, \forall i:c_i \leq C$, 令 $S_n$ 为和, $E_n$ 为期望值, $V_n$ 为方差

$\bullet$ Hoeffding 不等式表示

$\bullet$ 当求和方的方差与其几乎确定的边界相比较时, Bennett 不等式相对于 Hoeffding 进行了一些改进

重对数律 (Law of the iterated logarithm) 也是一种极限定理, 概率论中重对数律描述了随机游动的波动幅度^[14].

设 $X_i$ 为取值 1 和 $-1$ 的独立同分布随机变量, 且取值等概率. 令 $S_n=\sum\limits^n_{i=1} X_i$, 那么 $\mu =E(X_i)=0,\ \sigma^2 = Var(X_i)=1$, 如何精确地描述 $S_n$ 的变化范围?

由重对数律, 对于均值为 $\mu$, 方差为 $\sigma^2$ 的独立同分布随机变量 ${X_i}$,

代入 $\mu =0, \sigma^2 =1$, 可以认为: 对于任意的 $\varepsilon >0$, 只存在有限多个 $n \in N$, 使得

因为 ${X_i}$ 本身是关于 0 对称的, 反过来也成立. 即只存在有限多个 $n \in N$, 使得

所以可以构造区间

此时只有有限多个 $S_n,\ n\in N$, 落在这个区间外面. 因为我们考虑的是 $n \rightarrow 0$ 的情况, 有限个落在区间外的点可以忽略. 所以这个范围可以包含 $S_n$ 的波动, 并且小一点点也不可以, 所以这个区间是精确的^[15].

总的来说, $|S_n| \leq n$, 但是大的 $|S_n|$ 出现的概率小, 实际上 $S_n$ 的取值范围比 $[-n,n]$ 窄得多. 弱大数定律和强大数定律表明 $\frac{S_n}{n}\stackrel{P}{\longrightarrow} 0$, 甚至 $\frac{S_n}{n}\stackrel{a.s.}{\longrightarrow} 0$, 其中 $\stackrel{P}{\longrightarrow}$ 表示概率收敛, $\stackrel{a.s.}{\longrightarrow}$ 表示几乎肯定收敛. 因此, $S_n$ 从 0 开始的偏差比线性增长要慢得多. 另一方面, 中心极限定理指出 $\frac{S_n}{n}\stackrel{D}{\longrightarrow} N(0,1)$ ($\stackrel{D}{\longrightarrow}$ 表示依分布收敛), 在某种意义上 $S_n$ 是波动的下界, 它们将离开区间 $[-\sqrt n, \sqrt n]$, 因为 $\sup\limits _{n \rightarrow \infty} \frac{S_{n}}{\sqrt{n}}=\infty$ (由 0-1 Kolmogorov 定律可得). 事实证明, 波动可以更准确地估计^[16,17]. 因此, 比起大数定律和中心极限定律, 重对数律可以精确地描述随机变量前 $n$ 项和 $S_n$ 的变化范围. 图2 采用 $n$ 从 1 到 1000, 来测试重对数律对 $S_n$ 的边界估计.

其中虚线为 $\pm \sqrt n$, 实线为 $\pm \sqrt{2n\log \log n}$. 实线对随机游走 $S_n$ 的边界估计更精确一点. 特别地, 当 $n$ 足够大时, 落在实线外面的点只有有限多个. 因此, 归一化 $S_n$ 除 $n$ 就太强了, 而除 $\sqrt n$ 就太弱了. $S_n$ 从 0 开始的波动与 $\sqrt{2n\log \log n}$ 成正比.

还有一个有趣的性质. 定义 $S_n^{[i]} = \frac{S_n}{\sqrt{2n\log \log n}}$. 重对数定律意味着 $S_n^{[i]}$ 不会向任何常数收敛. 但是, 它在概率上收敛到 0. 修正一些 $\varepsilon > 0$, 对于几乎所有的 $n$, 在 $p<1$ 的任意高概率下, 过程 $S_n^{[i]}$ 不会离开 $ (-\varepsilon, \varepsilon)$. 另一方面, 表明这个过程会在这个区间之外无限次. 这个明显的矛盾表明, 我们的直觉对发生在无穷远处的现象是不可靠的.

下面考虑更一般的情形.

令 $(B_i)_{i \geq 0}$ 为具有参数 $p\in (0,1)$ 的伯努利过程, 即具有相同分布 $P(B_i=1)=1-P(B_i=0)=p$ 的一系列独立随机变量. 通常情况下 $p=1/2$, 考虑以下转换过程

序列 $X_i$ 取值 ${-1, +1}$, 过程 $(S_n)_{n\in N}$ 被称为一个随机游走.

定理 3.1^[18] 对于均值为 $\mu$, 方差为 $\sigma^2$ 的独立同分布随机变量 ${X_n}$, 有

上面我们简要介绍了几类偏差不等式, 经过公式推导, 发现 Hoeffding 不等式和 Bennett 不等式对自变量和的界控制更严格.

首先考虑 Hoeffding 不等式, 同样以伯努利分布作为样本来估计. 此时有不等式

对于伯努利分布, $S_n=n\hat{p}, E_n=np$, 不等式化为

同样, 我们利用假设检验的思路, 显著性水平为 $\alpha$. 令 $2{\rm e}^{-\frac{2t^2}{n}}=\alpha$, 计算得到 $t=\sqrt{\frac n2 \log\frac2\alpha}$, 此时不等式化为

由此可以得到 $p$ 的 $1-\alpha$ 的置信水平区间为 $[\hat{p}_L, \hat{p}_U]$, 其中

考虑 Bennett 不等式, 同样有

显著性水平为 $\alpha$, 令 $2 \exp \left[-\frac{V_{n}}{C^{2}} h\left(\frac{C t}{V_{n}}\right)\right]=\alpha$, 计算得到 $\frac tn = h^{-1}(\frac1{n\sigma^2}\log\frac2\alpha)\sigma^2$, 此时不等式化为

故 $p$ 的 $1-\alpha$ 的置信水平区间为 $[\hat{p}_L, \hat{p}_U]$, 其中

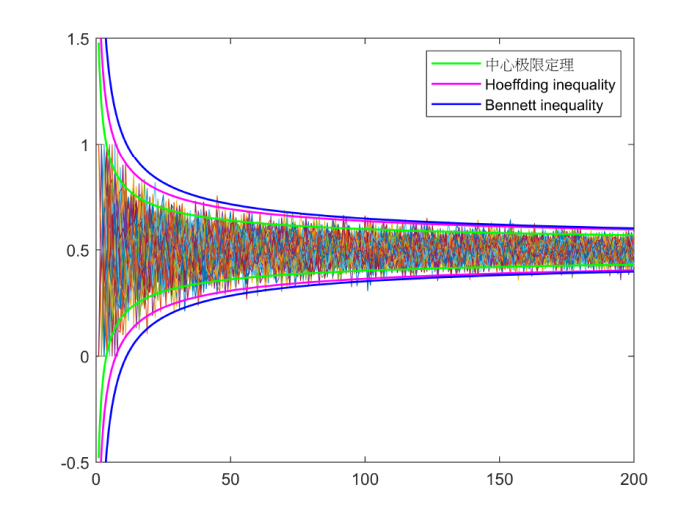
至此, 已经得到了基于 Hoeffding 不等式和 Bennett 不等式的置信带, 那么这个置信带与中心极限定理比较如何呢? 下面根据三种置信区间形成三类置信带如下图3 所示.

由图中可以看到, 基于 Hoeffding 不等式和 Bennett 不等式得到的置信带均要比中心极限定理要宽, 这说明该不等式对独立同分布随机变量和的控制不如中心极限定理准确, 这与预期的不符. 试图找到一条比中心极限定理更窄的置信带, 下面考虑重对数律.

回顾前面介绍的重对数律: 对于均值为 $\mu$, 方差为 $\sigma^2$ 的独立同分布随机变量 ${X_n}$, 有

下面利用重对数律来对 $S_n$ 进行估计

对参数为 $p$ 的伯努利分布而言, 上述 $\mu=p, \sigma^2=p(1-p)$, 进一步得到

由此 $p$ 的置信区间近似为区间

下面将重对数律得到的置信区间与中心极限定理进行对比. 可以看到, 基于重对数律得到的置信区间在一定程度上要比中心极限定理要更小一点, 即对频率序列的估计要更为严格一点. 如图4 所示.

由图4 可以看出, 置信区间并不能完全包裹住所有频率序列, 总会有部分点落在置信区间之外, 这是正常的情况. 我们需要设定一个阈值, 当落入置信区间点的个数与 $n$ 的比值大于该阈值时, 就可以做出肯定的判断. 所以可以说当频率序列收敛时, 有很大概率落入定义的置信区间内.

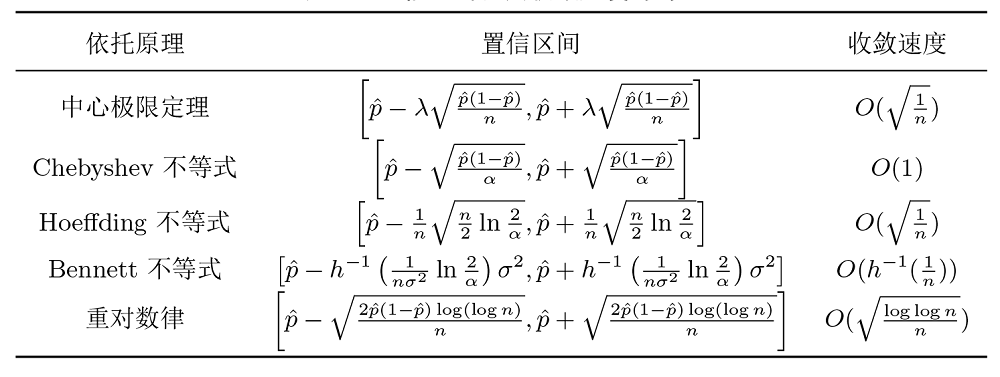
上面我们基于偏差不等式和重对数律推导得到了各种置信区间, 本质上来说稳定集合的收敛区间是收敛 (无论哪种收敛). 速度上的比较主要取决于各个收敛区间边界的收敛速度, 收敛速度见表1. 表中可以看出, 中心极限定理得到的置信区间收敛速度和 Hoeffding 不等式是一样的, 而重对数律的置信区间收敛速度最快.

下面给出稳定集合判别的新标准.

定义 4.1 给定时间序列样本

及样本 $X_L$ 掉到集合 $A$ 的概率为 $f$, 已知集合 $A \subseteq \Omega$, (2.1) 式产生频率序列$\left\{f_{k}(A)\right\}_{k=1}^{L}$, 定义区间序列

若 $P_{C, A}(f) \geq p_{0}$, 则称集合 $A$ 为 $X_L$ 的稳定集合, 该稳定集合判别标准记为 $C(p_0)$.

两种置信区间的比较

进一步有

这里 $\lambda$ 取 1.96, 可以看出 $n$ 在很大范围内都能保证重对数律的严格性.

前面利用一阶自回归模型 $AR(1)$ 验证了基于中心极限定理得到的非平稳性度量指标 $NS$ 的合理性, 实验证明该指标是合理的, 我们需要对新标准的合理性进行验证.

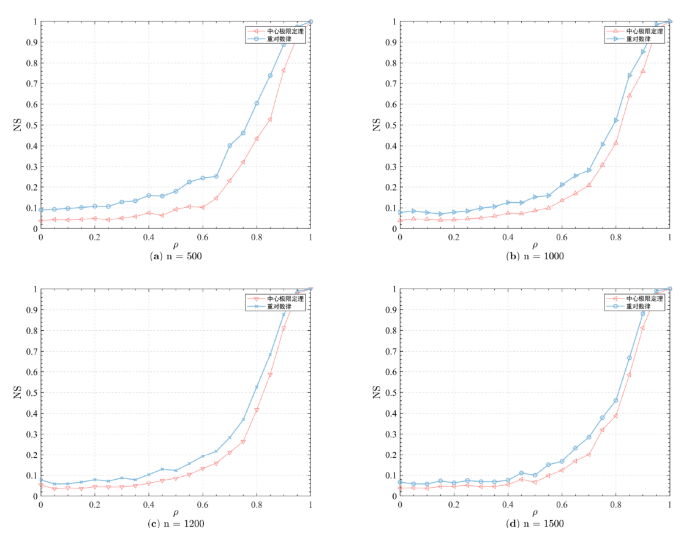
下面进行前面相同的实验, 选择样本长度 $L=500\;1000\;1200\;1500$, 样本组数 $S=200$, $NS$ 设置: 等分位数下划分 $N=\left\lfloor 1.87(L-1)^{0.4}\right\rfloor, \lambda=1.96, p_0=0.925$. 模型 $AR(1)$ 中的扰动项 $\varepsilon$ 服从独立正态分布. 实验结果分别如下图5 所示.

可以看出, 基于重对数律计算得到的 $NS$ 值始终比基于中心极限定理计算得到的 $NS$ 值要大. 随着数据长度 $n$ 的增大, 两者越来越接近, 这也与之前的推导相符. 这意味着在同样条件下, 对同一个稳定集合的判别, 基于重对数律的判别标准要更加严格一点, 并且提高了非平稳性度量在 $NS$ 较小时的分辨率.

非平稳性度量的一个广泛应用是模型选择, 通过分析残差序列的非平稳程度可以得到一个更为精确的模型. 令 $y$ 为观测信号, 其表示为

其中 $f$ 为真实的模型, $\varepsilon$ 为噪声序列. 第 $i$ 个观测数据的残差序列为

如果模型正确地拟合数据, 则残差序列将接近于随机噪声. 利用文献 [19] 提出的基于非平稳性度量的复杂噪声下的参数校准方法, 来对复杂模型的参数进行校准. 基于之前的研究^[20], 0.05 的值可作为阈值, 以确定估计残差序列中是否存在任何趋势. 如果估计的残差序列的 $NS$ 值小于 0.05, 则表明残差序列中没有趋势, 相应的 $\theta$ 估计是准确的.

对于残差序列 $\widehat{\varepsilon}_t(\hat{\theta})=y(t)-f(t ; \hat{\theta})$, $NS(\hat{\theta})$ 表示为 $\widehat{\varepsilon}_t(\hat{\theta})$ 的 $NS$ 值, 计算步骤如下

(1) 通过高斯-牛顿法获得复杂噪声模型的估计参数 $\hat{\theta}$, 作为参数校准的初始值, 记作 $\hat{\theta}^{(0)}$;

(2) 计算 $NS(\hat{\theta}^{(0)})$ (通常大于 0.05);

(3) 沿着 $NS$ 值减少的方向变化 $\hat{\theta}^{(0)}$, 步长设置为一个较小的固定值 (设为 0.01);

(4) 令 $\hat{\theta}^{(k)}$ 为第 $k$ 步的参数值. 重复之前的步骤直到满足:

(5) 最后得到准确估计值: $\theta^{\prime}=(1 / i)(\hat{\theta}^{(k)}+\hat{\theta}^{(k+1)}+\cdots+\hat{\theta}^{(k+i-1)})$.

考虑复杂信号单参数模型

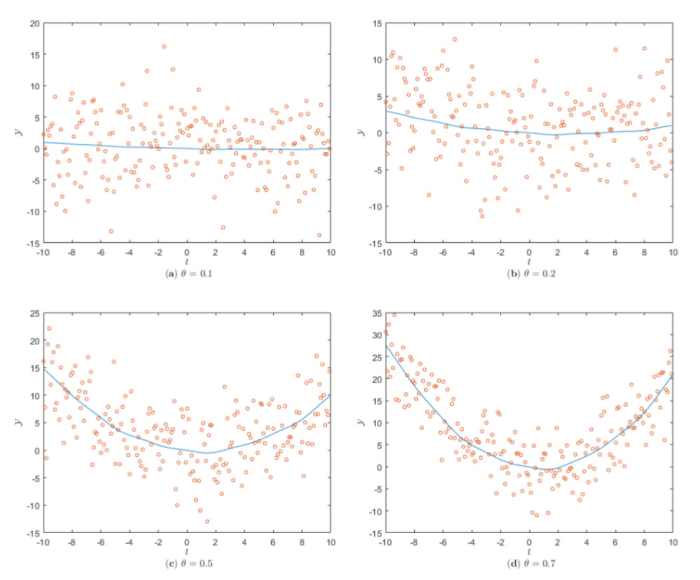
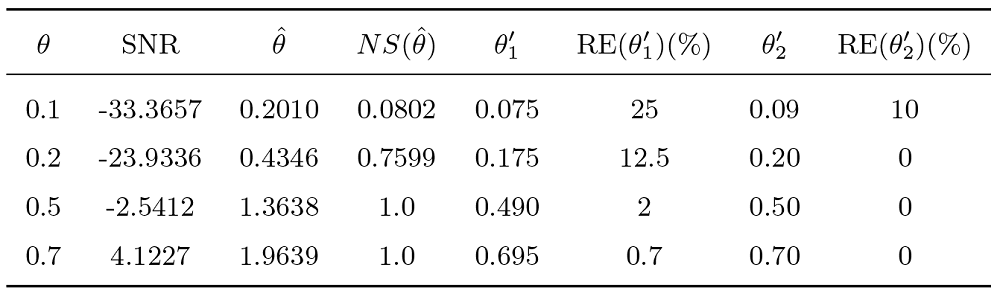
为进一步分析参数值对校准的影响, 选取四个 $\theta$ 值进行验证. 图6 显示模型的生成信号, 可以看出当参数值比较小时, 噪声的影响较大, 此时信噪比 SNR 为负.

图7 显示了参数校准的过程, 只针对参数比较接近的图像部分进行显示. 图中可以看出, 不同参数的估计值可以校准到精确值. 当校准停止时, $NS < 0.05$. 特别地, 当参数较小时, SNR 为负, 但仍可以通过 NS 将参数校准到精确值.

参数校准的结果见表2, 对于不同的参数 $\theta$, 基于重对数律的非平稳性度量在参数校准方面均比中心极限定理的更为准确. 在参数值较大时, 均能保持 0 的相对误差. 对于参数值较小的复杂模型, 此时模型中噪声占主导地位, 参数校准的困难比较大, 但是新方法仍能将参数校准到一个合理的范围, 且得到的相对误差较低, 跟原有方法相比相对误差有显著的提升. 某种程度上来说, 新方法提高了模型选择的精度, 这点由重对数律得到的稳定集合判别标准更为严格来保证, 并且该方法只有一个参数, 使得调参更为方便. 对于一些实际应用中更加复杂的数据, 可以通过该方法来筛选一些合适的模型.

本文回顾了非平稳性度量的理论研究框架, 并且对原有的稳定集合判别标准提出了一些值得研究的问题. 如何提高非平稳性度量在 $NS$ 较小时的分辨率, 可以通过调节参数的大小来控制判别标准的尺度, 但其精度终归是有限度的. 这就启发我们寻求一种新的判别标准, 使得在同样条件下, 新标准能够区分一些在原有标准下稳定性相近的集合, 提高在 $NS$ 较小时的分辨率. 在尝试一些偏差不等式如 Hoeffding 不等式、Bennett 不等式后, 发现重对数律对自变量和的估计更加精确, 相较于原有的基于中心极限定理得到的稳定集合判别标准, 基于重对数律得到的判别标准更为严格. 并且重对数律是几乎必然收敛的, 所需的参数更少, 满足对收敛性更高的要求. 对于非确定性信号, 基于重对数律的非平稳性度量也表现出更强的收敛性, 对模型的稳定性要求更高. 在模型选择方面, 对于含噪声的复杂模型的参数校准, 新方法表现出更好的校准效果, 得到的参数值更精确. 即使对噪声比较强的模型, 该方法也能够达到较低的相对误差, 且优于原来的方法. 这在一定程度上提高了模型选择的精度, 有助于筛选出更合适的模型.

另外, 反正弦律也是对随机游走的刻画, 描述了随机游走在轴上方 (下方) 的概率分布情况^[21], 这对非平稳性度量的研究可能有帮助.