1 引言
设 Ω 是 Rn 中的一个有界集, 并且具有光滑边界 ∂Ω. 本文主要研究 Ω 上两个弱耦合弹性板的长时间渐近行为, 其中仅有一个板带有阻尼. 具体的, 本文所研究的弱耦合系统可描述为
其中, u(x,t) 和 v(x,t) 分别表示 t 时刻 x∈Ω 处板的位移; α>0 为耦合系数, 并且假定它足够小; 常数 η>0 为阻尼系数; (−Δ)βvt,β=0,1,2 代表三种不同类型的阻尼[11], 即粘性阻尼 (β=0, 也称为摩擦阻尼), 结构阻尼 (β=1) 和 Kelvin-Voigt 阻尼 (β=2). 弱耦合板系统 (1.1) 可以看作 Russell[33]提出的一般性框架的一个特例. 这类模型可以用来描述塑性复合材料的振动, 这类材料广泛应用于飞行器、舰船、潜艇等. 众所周知, 振动在工程中往往起着消极的作用, 因此通常需要对这类系统施加各种类型的阻尼来抑制振动[35].
注意到当耦合系数 α=0 时, 系统 (1.1) 将解耦成一个保守板 (u 系统) 和一个阻尼板 (v 系统). 已有研究表明, 具有上述三种不同类型阻尼的板方程对应的半群都是指数稳定的. 特别地, 在结构阻尼和 Kelvin-Voigt 阻尼情形半群还是解析的[11,21,22]. 一个自然的问题是, 当耦合系数 α>0 时, 保守的 u 系统能否通过耦合作用被另一个带有阻尼的 v 系统间接镇定. 关于该问题已有许多研究结果. 一般来说, 不同于单一阻尼系统的指数衰减, 弱耦合波方程或板方程往往只具有慢衰减性, 比如多项式衰减、对数衰减[5]. 而间接阻尼的类型 (阻尼阶数 β) 与耦合系统 (1.1) 最优衰减率之间的关系则是本文的主要研究内容.
定义系统 (1.1) 的自然能量如下
直接计算可得
这表明系统 (1.1) 是耗散的. 而且, 由 (1.3) 式可以看出, 系统 (1.1) 的能量耗散只依赖于耦合系统中的 v 部分, 而与保守的 u 部分无关. 换句话说, 保守板方程是通过耦合作用被耗散板方程的阻尼效应间接镇定的. 正因为如此, 该类问题也称为间接控制或间接镇定问题[33]. 耦合弹性板系统的间接镇定问题已有广泛的研究. 20 世纪 90 年代, Russell[33]提出了一个关于弹性系统间接阻尼问题的一般性框架. 此后, 大量有关间接控制和间接镇定问题的研究成果开始出现. 例如, 关于带有间接粘性阻尼的弱耦合双曲系统 (耦合波方程、板方程或波-板系统) 的多项式稳定性或对数稳定性研究, 可参考文献 [4⇓-6,14,16,17,23,25,34,38]; 关于强耦合 (通过速度耦合) 波方程或板方程的能量衰减率研究, 可参考文献 [7,12,15]; 关于具有间接阻尼的耦合弹性板或波系统的正则性和稳定性研究, 可参考文献 [9,18,20,26]; 关于耦合板方程或波方程的间接边界镇定问题研究, 可参考文献 [3,29,32]. 需要注意的是, 有关该类问题的研究很多, 这里仅列出了部分文献. 带有其它类型间接阻尼的耦合系统稳定性研究也有一些很好的结果, 比如关于热阻尼[13,36,37]、分数阶阻尼[2,30]的研究.
前面提到的结果主要集中在具有粘性阻尼 (β=0) 耦合系统的稳定性或者具有结构阻尼 (β=1)、Kelvin-Voigt 阻尼 (β=2) 系统的正则性. 此外, 利用 Riesz 基方法, 文献 [28] 还研究了具有负阶 (β<0) 间接阻尼的抽象弱耦合双曲系统的长时间行为. 他们给出了系统算子谱的渐近表达式, 并得到了系统的最优多项式衰减率. 受文献 [28] 启发, 本文致力于研究弱耦合板系统 (1.1) 的最优衰减率及其与阻尼阶数 β=0,1,2 的关系. 对于该问题, 据我们所知, 现有文献中尚未涉及带有间接结构阻尼或 Kelvin-Voigt 阻尼的高维弱耦合板系统的稳定性. 正如前面所述, 带有直接结构阻尼或 Kelvin-Voigt 阻尼的非耦合板方程不仅是指数稳定的, 而且是解析的, 但带有粘性阻尼的非耦合板则不具有这种正则性. 然而, 本文中我们发现一个有趣的现象, 尽管间接结构阻尼或 Kelvin-Voigt 阻尼比粘性阻尼``更强" (阻尼阶数更高), 但带有间接结构阻尼或 Kelvin-Voigt 阻尼的弱耦合板系统的衰减速度反而要比具有粘性阻尼的弱耦合板系统慢得多.
本文的创新之处主要体现在以下两方面: 一方面, 通过细致的谱分析, 推导出了具有不同类型阻尼的系统算子谱的渐近表达式, 并进一步通过谱的实部、虚部之间的关系得到了弱耦合系统多项式衰减率的最优性. 另一方面, 基于频域方法, 我们得到了 β=0,1,2 时系统 (1.1) 精确的多项式衰减率. 此外, 我们还发现了一个有趣的现象, 即间接阻尼的阶数越高, 耦合板系统 (1.1) 衰减越慢.
本文结构安排如下: 第 2 节给出本文的主要结果. 第 3 节中, 利用半群理论证明了系统的适定性. 第 4 节给出系统算子谱的渐近分布. 通过分析发现, 无论阻尼阶数取 0, 1 或 2, 算子的谱总存在一个趋近于虚轴的分支, 这意味着弱耦合系统不具有指数稳定性. 第 5 节中进一步证明了系统 (1.1) 是多项式稳定的, 并得到了最优多项式衰减率和间接阻尼阶数 β 之间的关系. 最后, 在第 6 节对系统 (1.1) 的谱分布和动力学行为进行了数值模拟, 验证了理论结果的正确性.
2 主要结果
令 V(Ω)=H2(Ω)∩H10(Ω), 定义 Hilbert 状态空间
内积定义为
其中, Ui=(ui,yi,vi,zi)∈H,i=1,2. 容易验证, 当 α>0 充分小时, H 成为一个 Hilbert 空间.
定义系统算子 Aβ,β=0,1,2 如下,
∙ 当 β=0 (粘性阻尼) 时,
定义域为
∙ 当 β=1 (结构阻尼) 时,
定义域为
∙ 当 β=2 (Kelvin-Voigt 阻尼) 时,
定义域为
则系统 (1.1) 可写为状态空间 H 中的发展方程
其中, U(t)=(u(⋅,t),y(⋅,t),v(⋅,t),z(⋅,t)), U0=(u0(⋅),u1(⋅),v0(⋅),v1(⋅))∈H.
下面的定理 2.1 建立了系统 (2.6) 的适定性.
定理 2.1 设算子 Aβ,β=0,1,2 及空间 H 定义如前所示, 则有如下结果成立
(1) 0∈ρ(Aβ), 其中, ρ(Aβ) 表示算子 Aβ 的预解集;
(2) 对 β=0,1,2, 算子 Aβ 总是生成 H 上的 C0 压缩半群 {etAβ}t≥0.
通过对系统算子 Aβ 细致的谱分析, 可以得到如下关于算子 Aβ,β=0,1,2 的本征值的渐近表达式.
命题 2.1 算子 Aβ,β=0,1,2 定义如前所述, {μk}k∈N∗ 为简单支撑边界条件下拉普拉斯算子 −Δ 的本征值. 则算子 Aβ 的本征值包含两个分支, 分别记为 {λ1,k}, {λ2,k}, 并且具有如下渐近表达式
(1) 当 β=0 时,
(2) 当 β=1 时,
(3) 当 β=2 时,
由 (2.7)-(2.9) 式给出的渐近表达式容易看出, 对 β=0,1,2, 虚轴总是算子 Aβ 的特征值的渐近线, 这意味着系统 (2.6) 达不到一致指数衰减.
推论 2.1 对 β=0,1 或 2, 系统 (2.6) 均不是一致指数衰减的.
下面进一步研究系统 (2.6) 的慢衰减率, 本文的主要结果如下.
定理 2.2 对任意初值 U0∈D(Aβ), 系统 (2.6) 是多项式稳定的, 且最优衰减率为 12+β, β=0,1,2. 即存在常数 C>0, 满足
注 2.1 定理 2.2表明, 随着阻尼阶数 \beta 的增大, 多项式衰减率 \frac{1}{2 + \beta},\; \beta=0, 1, 2 将变小. 换句话说, 随着阻尼的阶数从 \beta=0 逐渐增大到 \beta=1, \beta=2 (分别对应粘性阻尼、结构阻尼、Kelvin-Voigt 阻尼), 系统 (1.1) 将会衰减越来越慢.
注 2.2 与弱耦合系统相关的一些其它方面的问题也值得进一步研究, 例如
3 适定性 (定理 2.1 的证明)
本节证明系统 (2.6) 的适定性, 分为以下两部分
(1) \mathcal{A}_\beta 耗散
对 U=(u,y,v,z)\in D(\mathcal{A}_\beta), 直接计算可得
从而,
因此, 算子 \mathcal{A}_\beta 是耗散的.
(2) \mathcal{A}_\beta 是双射
首先证明 \mathcal{A}_\beta 是单射. 设 W=(\hat u, \hat y, \hat v, \hat z)\in \mathcal{D}(\mathcal{A_\beta}) 满足 \mathcal{A}_\beta W=0, 只需说明 W=0. 由 \mathcal{A}_\beta 的定义 (2.3)-(2.5) 式, 有
并且满足如下边界条件
根据 (3.2)_1 式和 (3.2)_3 式, \hat y=0, \hat z=0, 还需进一步说明 \hat u=\hat v=0. 一方面, 将 (3.2)_2 式和 (3.2)_4 式相加得 \Delta^2 (\hat u+\hat v) + (1+\alpha)(\hat u+\hat v)= 0, 注意到边界条件 (\hat u + \hat v)|_{\partial \Omega} = (\Delta \hat u +\Delta\hat v)|_{\partial \Omega} =0, 从而有 \hat u +\hat v=0. 另一方面, (3.2)_2 式与 (3.2)_4 式相减得 \Delta^2 (\hat u-\hat v) +(1-\alpha) (\hat u-\hat v) = 0, 根据边界条件 (\hat u - \hat v)|_{\partial \Omega} = (\Delta \hat u - \Delta\hat v)|_{\partial \Omega} =0 可得 \hat u -\hat v=0. 因此, \hat u =\hat v=0. 这说明 \mathcal{A}_\beta 是单射.
下面证明 \mathcal{A}_\beta 是满射. 只需说明对任意的 F=(e,f,g,h) \in \mathcal{H}, 存在 U = (u,y,v,z)\in \mathcal{D}(\mathcal{A}_\beta) 使得
即
设 (\xi,\zeta)\in V(\Omega)\times V(\Omega), 分别用 \bar{\xi} 和 \bar{\zeta} 乘以 (3.4)_2 式和 (3.4)_4 式并积分, 两式相加得
其中
直接验证可知, a 是 V(\Omega)\times V(\Omega) 上满足连续性和强制性的一个双线性形式, L 是 V(\Omega) 上满足连续性的一个线性形式. 根据 Lax-Milgram 定理, 变分问题 (3.5) 存在唯一解 (u,v)\in V(\Omega)\times V(\Omega).
为了证明 U=(u, y, v, z)\in\mathcal{D}(\mathcal{A}_\beta) 的存在性, 还需要说明当 \beta=0,\,1 时, 有 \Delta u,\;\Delta v\in H^2(\Omega), 当 \beta=2 时, 有 \Delta u, \Delta v + \eta \Delta z \in H^2(\Omega). 显然, 根据 (u,v)\in V(\Omega)\times V(\Omega) 和 (3.4) _2 式可知 \Delta u\in H^2(\Omega). 当 \beta=0,\,1 时, 综合 (u,v)\in V(\Omega)\times V(\Omega), (3.4)_3 式及 (3.4)_4 式可得 \Delta v\in H^2(\Omega); 当 \beta=2 时, 根据 (u,v)\in V(\Omega)\times V(\Omega) 和 (3.4)_4 可得 \Delta v + \eta \Delta z \in H^2(\Omega). 因此, 存在 U = (u,y,v,z)\in \mathcal{D}(\mathcal{A}_\beta) 使得 (3.3) 式成立.
根据 Lumer-Phillips 定理[31], 可知 \mathcal{A}_\beta 生成 \mathcal{H} 上的一个 C_0 压缩半群 \{{\rm e}^{t\mathcal{A}_\beta}\}_{t\geq 0}, 这样就完成了系统 (1.1) 的适定性证明.
4 谱分析 (命题 2.1 的证明)
本节主要给出系统算子 \mathcal{A}_\beta,\; \beta=0,1,2 谱的渐近分布. 考虑本征值问题 (\lambda I - \mathcal{A}_\beta) U = 0, 即
在系统 (1.1) 简单支撑边界条件下, 拉普拉斯算子 -\Delta 的本征值及相应的本征向量分别记为 \left\{\mu_k\right\}, \left\{\Phi_k\right\}, 其满足当 k \rightarrow +\infty 时, \mu_k \rightarrow +\infty. 令
其中 C, D 为常数. 将 (4.2) 式代入 (4.1) 式得
因此, \lambda_k 是 \mathcal{A}_\beta 的本征值当且仅当
下面我们将从特征多项式 (4.3) 式出发推导本征值 \lambda_k 的渐近表达式. 根据 (4.3) 式, 本征值 \lambda_k 一定满足下面两个不等式之一
分以下两种情况讨论
情形 1 存在一支本征值 \left\{ \lambda_{1,k} \right\} 满足 \left| \lambda_{1,k}^2 + \mu_{k}^2 + 1 \right| \leq \alpha.
在这种情形下, 有 \lambda_{1,k}^2 + \mu_{k}^2 = O(1), 注意到当 k\rightarrow +\infty 时 \mu_{k}\rightarrow +\infty, 从而
为了给出 \lambda_{1,k} 更准确的估计, 可将 (4.3) 式等价转化为如下形式
将 (4.4) 式代入 (4.5) 式的右边, 通过泰勒展开可得
(i) 当 \beta = 0 时,
(ii) 当 \beta = 1 时,
(iii) 当 \beta = 2 时,
情形 2 存在一支本征值 \left\{ \lambda_{2,k} \right\} 满足
在这种情形下, 类似于情形 1 的讨论, 有
因此
对 (4.9) 式分子中的第二项应用泰勒展开, 可以得到对 \lambda_{2,k} 更准确的估计, 即 (2.7)-(2.9) 式, 具体细节此处省略.
这样就完成了命题 2.1 的证明.
5 稳定性分析 (定理 2.2 的证明)
引理 5.1 设 {\{T(t)\}_{t\geq 0}} 是 Hilbert 空间 {H} 中算子 A 生成的有界 C_0 半群, {\rm i} \mathbb{R}:=\{{\rm i}\gamma\,|\,\gamma\in\mathbb{R}\}\subset\rho({A}), 且 s>0. 则下面两条表述是等价的
(\rm i) 存在一个常数 c>0, 使得对任意的 U_0\in \mathcal{D}({A}), 有
定理 2.2 的证明 只需证明 {\rm i} \mathbb{R}\subset\rho(\mathcal{A}_\beta) 以及引理 5.1 中的条件 (ii) 对 s=2+\beta 成立. 分为以下两部分
(1) {\rm i} \mathbb{R} \subset \rho (\mathcal{A}_\beta).
用反证法, 假设 {\rm i}\mathbb{R}\nsubseteq\rho(\mathcal{A}_\beta). 注意到 0\in \rho(\mathcal{A}_\beta) 且 \rho(\mathcal{A}_\beta) 是 \mathbb{C} 中的一个开集, 从而有 0<\widetilde \lambda_\beta<\infty,\; \beta=0,1,2, 其中
根据 Banach-Steinhaus 定理[27], 存在序列 U_{n}=(u_n, y_n, v_n, z_n)\in \mathcal{D}(\mathcal{A}_\beta), \|U_{n}\|_{\mathcal{H}}=1, 以及 \lambda_{n}\in \mathbb{R}, \lambda_{n}\to \widetilde{\lambda}_\beta, 满足
即
下面说明如下定义的量当 n\rightarrow\infty 时都收敛到 0,
这类量以下记为 o(1).
由 (5.1) 式和 (3.1) 式可得,
根据 (5.2)_3 式及 \lambda_n\to \widetilde{\lambda}_\beta,
其中, \beta=1 时应用了 Poincaré 不等式. 将 (5.2)_1 式代入 (5.2)_2 式, 并在 L^2(\Omega) 中和 v_n 作内积得
同理, 将 (5.2)_3 式代入 (5.2)_4 式, 并在 L^2(\Omega) 中和 u_n 作内积得
(5.7) 式与 (5.6) 式相减并取实部, 则
此外, 根据 (5.4) 式和 (5.5) 式,
代入 (5.8) 式得
为了证明 (5.3) 式成立, 分以下两种情形讨论
情形 1 \beta=0, 1. 在这种情形下, 根据 (5.5) 式可知 \|v_n\|_{L^{2}(\Omega)}=o(1), 结合 (5.9) 式有
进一步, 根据 (5.2)_1 式可得
在 L^2(\Omega) 中分别对 (5.2)_2 式和 u_n, 以及 (5.2)_4 式和 v_n 作内积, 通过分部积分可得
结合 (5.5)_1, (5.5)_2, (5.10), (5.11) 式, 有
最后, 综合 (5.5)_1, (5.5)_2, (5.10), (5.11) 和 (5.12) 式可得 \|U_n\|_{\mathcal{H}}=o(1), 这与 \|U_n\|_{\mathcal{H}}=1 矛盾.
情形 2 \beta=2. 考虑到 (5.5)_3 式以及 \|v_n\|_{L^{2}(\Omega)} 的有界性, 并通过分部积分, 有
进一步, 根据 Poincaré 不等式,
由 (5.2)_3 式可知
类似于 (5.9)-(5.12) 式中的分析可知
再结合 (5.5)_3, (5.14) 和 (5.15) 式就得到矛盾 \|U_n\|_\mathcal{H}=o(1).
综合以上两种情形, 总是成立 {\rm i} \mathbb{R} \subset \rho (\mathcal{A}_\beta).
(2) 下面证明
其中
运用反证法. 假设 (5.16) 式不成立, 根据 Banach-Steinhaus 定理, 存在序列 U_{n}=(u_n, y_n, v_n, z_n)\in D(\mathcal{A}_\beta) (\|U_{n}\|_{\mathcal{H}}= 1) 及 \lambda_{n}\in \mathbb{R} (\lambda_{n}\to \infty), 使得
其中 j 满足 (5.17) 式. 更具体的, (5.18) 式可写为
根据耗散性 (3.1) 式, 有
结合 (5.18) 式, 可得
进一步, 根据 (5.19)_3 式, 当 \beta=0,1,2 时, 总有
将表达式 (5.17) 代入 (5.22) 式得
其中, \beta=1 时应用了 Poincaré 不等式. 将 (5.19)_1 式代入 (5.19)_2 式, 并在 L^2(\Omega) 中与 v_n 作内积得
类似地, 将 (5.19)_3 式代入 (5.19)_4 式, 并在 L^2(\Omega) 中与 u_n 作内积可得
为了推导出矛盾, 接下来证明 \|U_n\|_{\mathcal{H}}\to 0. 根据 \beta 的不同取值, 分为以下三种情况
(1) \beta = 0.
在这种情况下, 由 (5.17) 式可知 j = \frac{1}{2}, 此时 (5.21) 式即
一方面, 根据 (5.26)_1 式, 容易发现 (5.24) 式右边的第一项、第四项和第五项都趋于零, 因此
另一方面, 根据 (5.19)_1, (5.23)_1 和 (5.26) 式, 易知 (5.25) 式右边的第一项、第五项和第六项都趋于零, 从而有
(5.27) 式与 (5.28) 式相减得
结合 (5.19)_1 式可知
在 L^2(\Omega) 中, 分别对 (5.19)_2 式和 \lambda_n^{-2} u_n, 以及 (5.19)_4 式和 \lambda_n^{-2} v_n 作内积, 通过分部积分可得
注意到 (5.26)_1, (5.26), (5.29) 和 (5.30) 式, 从而有
最后, 综合 (5.23)_1, (5.26), (5.30) 和 (5.31) 式, 可以得到矛盾 \| U_n \|_{\mathcal{H}} \to 0.
(2) \beta = 1.
这种情况下, 由 (5.17) 式可知 j =\frac{1}{3}. 根据 (5.21) 式及 Poincaré 不等式, 有
(5.24) 式右边除以 \lambda_n, 并将 (5.23)_2 式代入 (5.24) 式, 可以看出第一项、第四项、第五项均趋于零, 这说明此时 (5.23) 式仍然成立. 同理, (5.25) 式两边同时乘以 \lambda_n^ {-1} 可得
通过分部积分,
根据 (5.19)_3, (5.23)_2, (5.32) 和 (5.34) 式可以看出, (5.33) 式右边第一项、第五项和第六项均趋于零, 此后的证明过程完全类似于 (5.28) 和 (5.31) 式, 此处不再赘述. 最后, 仍可推得 \| U_n \|_{\mathcal{H}} \to 0, 这与假设 \| U_n \|_{\mathcal{H}} =1 矛盾.
(3) \beta = 2.
这种情况下, 由 (5.17) 式可知 j = \frac{1}{4}. 根据 (5.21) 式, (5.23)_3 式以及 \| \lambda_nv_n \|_{L^2(\Omega)} 和 \| z_n \|_{L^2(\Omega)} 的有界性, 经过分部积分可得
进一步, 由 Poincaré 不等式可知,
(5.24) 式右边除以 \lambda_n^2 并将 (5.38) 式代入, 可以看出第一项、第四项、第五项均趋于零, 这说明 \beta=2 时 (5.27) 式仍然成立. 同理, (5.25) 式两边同时除以 \lambda_n^2, 并注意到系统 (1.1) 的边界条件, 有
根据 \|\Delta u_n\|_{L^2(\Omega)} 的有界性及 (5.21) 式和 (5.23)_3 式可知, (5.39) 式右边第四项满足
而且, 根据 (5.38) 式及 \|u_n\|_{L^2(\Omega)} 的有界性可知, (5.39) 式右边第五项趋于零, 从而
由 (5.23)_3, (5.27) 式以及 \|\Delta u_n\|_{L^2(\Omega)} 的有界性可知
从而, 由 (5.40) 式可得
根据 (5.41) 和 (5.19)_1 式,
类似于 (5.30)-(5.31) 式中的分析, 可知
综合 (5.23)_3, (5.37), (5.38), (5.41), (5.42) 及 (5.43) 式, 可知 \|U_n\|_{\mathcal{H}}=o(1), 这与 \|U_n\|_{\mathcal{H}}=1 矛盾.
基于以上分析, (5.16) 式总是成立的. 从而, 根据引理 5.1, 系统 (1.1) 是多项式稳定的, 并且衰减率至少为 \frac{1}{2+\beta},\; \beta=0,1,2.
下面还需要进一步说明系统 (1.1) 的衰减率 \frac{1}{2+\beta}, \beta=0, 1, 2 是最优的. 根据系统算子 \mathcal{A}_\beta,\; \beta=0, 1, 2 本征值的渐近表达式 (2.7)-(2.9), 可以看出, 总存在一支满足
这说明系统 (1.1) 的最优多项式衰减率为 \frac{1}{2+\beta},\; \beta=0, 1, 2 (文献 [19, 第 4 节]). 这就完成了定理 2.2 的证明.
6 数值仿真
本节给出算子 \mathcal{A}_\beta 谱的渐近分布及系统 (1.1) 动力学行为的数值模拟, 以此验证前面的理论结果. 为简单起见, 我们只考虑一维情况 \Omega=[0,1]. 系统参数选取为 \alpha=1,\;\eta=0.1, \beta 分别取 0,\;1,\; 2.
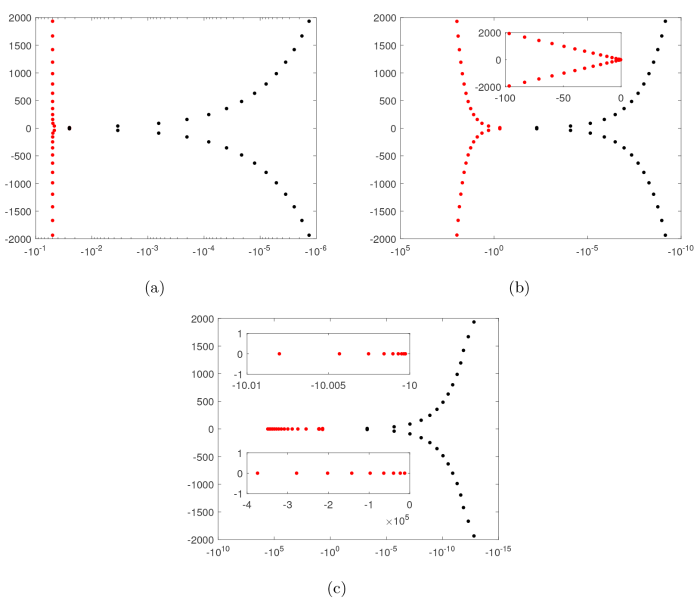
图1
从图1 可以看出, 算子 \mathcal{A}_\beta 的本征值包含两个分支, 在 \beta=0,\;\beta=1,\;\beta=2 三种情形下, 虚轴始终都是右边分支(黑色的点)的渐近线, 这与谱的渐近表达式 (2.7)-(2.9) 一致. 特别地, 通过比较 (2.7)-(2.9) 式的实部可以发现, \beta=0 时右边分支趋向于虚轴的速度最慢, 而当 \beta=2 时, 右边分支趋向于虚轴的速度最快, 这与图1 是一致的. 对于谱的左边分支 (红色的点), 图1(a), 1(b) 和 1(c) 之间存在明显差异. 具体来说, 当 \beta=0 时, 图1(a) 显示直线 \Re \lambda=-\frac{\eta}{2}=-0.05 是左边分支的渐近线; 当 \beta=1 时, 图1(b) 显示左边分支的渐近线为两条斜线, 斜率大致为 \pm 20; 当 \beta=2 时, 图1(c) 显示左边分支的特征值都是实数, 并且可以分为两部分, 一部分趋于 -\infty, 另一部分趋于聚点 -\frac{1}{\eta}=-10. 这些都与谱的渐近表达式 (2.7)-(2.9) 相吻合.
关于系统 (1.1) 动力学行为的模拟, 系统初值选取为
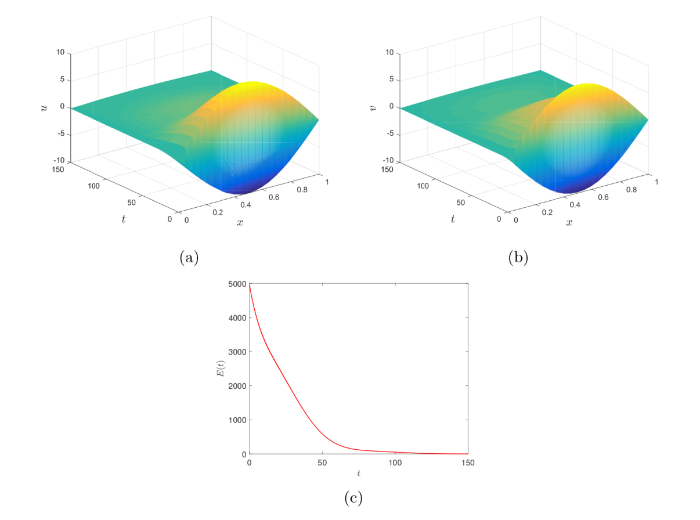
图2
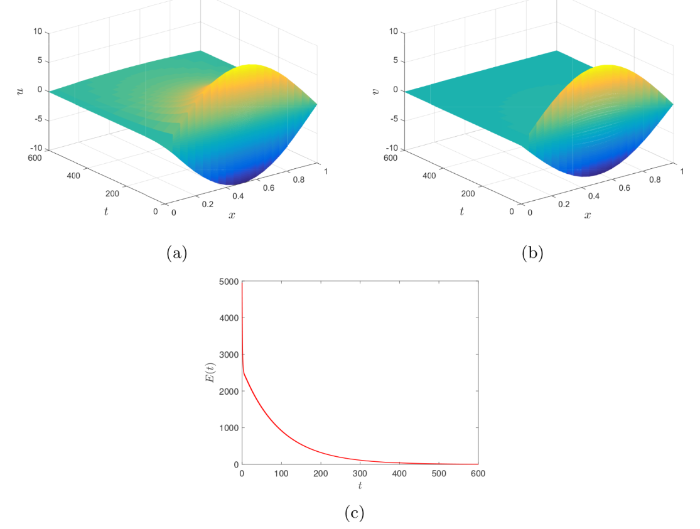
图3
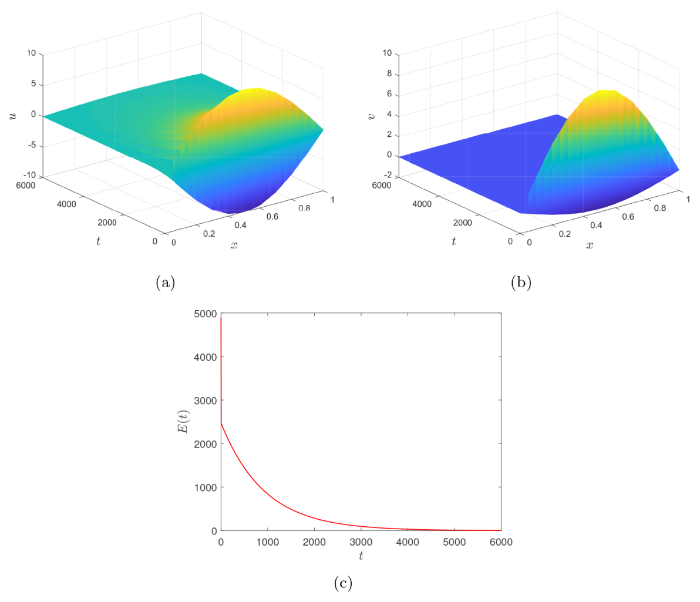
图4
由图2-4 可以看出, 对于不同类型的阻尼, 即 \beta 分别取 0, 1, 2 时, u(x,t) 和 v(x,t) 在 t\rightarrow +\infty 时总是收敛于零. 然而, 注意到图2-4 中较长的仿真时间 (图2中 T=150, 图3 中 T=600, 图4 中 T=6000), 可以看出收敛速度 (特别是 `u-部分') 不是很快, 这意味着弱耦合系统 (1.1) 没有达到指数衰减 (推论 2.1). 此外, 对比图2(c), 3(c), 4(c) 可以看出, 带有粘性阻尼 (\beta=0) 时系统 (1.1) 总能量 E(t) 衰减最快, 带有 Kelvin-Voigt 阻尼 (\beta=2) 时能量衰减最慢. 这与定理 2.2 中关于多项式衰减率的理论结果是一致的.
最后, 注意到图3(c) 和图4(c) 中, 系统能量 E(t) 在开始时衰减非常快. 实际上, 通过将图3(b), 4(b) 与图2(b) 进行比较, 容易发现图3(b), 4(b) 中弱耦合系统 (1.1) `v-部分'的衰减速度要比图2(b) 中快得多. 同时, 图3(a), 4(a) 中 `v-部分'的快速衰减导致相应的 `u-部分'衰减比图2(a) 中更慢. 这是合理的, 原因在于`v-部分'直接受到阻尼的影响, 而`u-部分'则通过与`v-部分'的耦合间接受到阻尼的影响. 因此, 一开始系统能量 E(t) 的快速衰减主要取决于 `v-部分', 而 `u-部分'和 `v-部分'的共同作用导致了 E(t) 后期的缓慢衰减.
参考文献
Stability results of locally coupled wave equations with local Kelvin-Voigt damping: Cases when the supports of damping and coupling coefficients are disjoint
Energy decay of some boundary coupled systems involving wave Euler-Bernoulli beam with one locally singular fractional Kelvin-Voigt damping
DOI:10.3934/mcrf.2021059 URL [本文引用: 2]
Indirect boundary stabilization of weakly coupled hyperbolic systems
DOI:10.1137/S0363012901385368 URL [本文引用: 2]
Indirect stabilization of weakly coupled systems with hybrid boundary conditions
DOI:10.3934/mcrf.2011.1.413 URL [本文引用: 1]
Indirect internal stabilization of weakly coupled evolution equations
DOI:10.1007/s00028-002-8083-0 URL [本文引用: 2]
Indirect stabilization of locally coupled wave-type systems
DOI:10.1051/cocv/2011106 URL [本文引用: 2]
A one-step optimal energy decay formula for indirectly nonlinearly damped hyperbolic systems coupled by velocities
DOI:10.1051/cocv/2016011
URL
[本文引用: 1]

In this paper, we consider the energy decay of a damped hyperbolic system of wave-wave type which is coupled through the velocities. We are interested in the asymptotic properties of the solutions of this system in the case of indirect nonlinear damping, i.e. when only one equation is directly damped by a nonlinear damping. We prove that the total energy of the whole system decays as fast as the damped single equation. Moreover, we give a one-step general explicit decay formula for arbitrary nonlinearity. Our results shows that the damping properties are fully transferred from the damped equation to the undamped one by the coupling in velocities, different from the case of couplings through displacements as shown in [F. Alabau, C. R. Acad. Sci. Paris Sér. I Math. 328 (1999) 1015–1020; F. Alabau, P. Cannarsa and V. Komornik, J. Evol. Equ. 2 (2002) 127–150; F. Alabau, SIAM J. Control Optim. 41 (2002) 511–541; F. Alabau-Boussouira and M. Léautaud, ESAIM: COCV 18 (2012) 548–582] for the linear damping case, and in [F. Alabau-Boussouira, NoDEA 14 (2007) 643–669] for the nonlinear damping case. The proofs of our results are based on multiplier techniques, weighted nonlinear integral inequalities and the optimal-weight convexity method of [F. Alabau-Boussouira, Appl. Math. Optim. 51 (2005) 61–105; F. Alabau-Boussouira, J. Differ. Equ. 248 (2010) 1473–1517].
Fractional-Feedback stabilization for a class of evolution systems
DOI:10.1016/j.jde.2019.11.022 URL [本文引用: 1]
Regularity and stability of the semigroup associated with some interacting elastic systems I: A degenerate damping case
DOI:10.1007/s00028-021-00738-7 [本文引用: 1]
Optimal polynomial decay of functions and operator semigroups
DOI:10.1007/s00208-009-0439-0 URL [本文引用: 1]
A mathematical model for linear elastic systems with structural damping
DOI:10.1090/qam/1982-39-04 URL [本文引用: 2]
Asymptotic stability of wave equations coupled by velocities
DOI:10.3934/mcrf URL [本文引用: 1]
Stability of abstract thermoelastic systems with inertial terms
DOI:10.1016/j.jde.2019.07.015 URL [本文引用: 1]
Sharp decay rates for the weakly coupled hyperbolic system with one internal damping
DOI:10.1137/110833051 URL [本文引用: 1]
Stabilization of the weakly coupled wave-plate system with one internal damping
DOI:10.1007/s10013-021-00493-9 [本文引用: 1]
Indirect stabilization of hyperbolic systems through resolvent estimates
Indirect stabilization of weakly coupled Kirchhoff plate and wave equations with frictional damping
DOI:10.1016/j.jmaa.2019.01.046 URL [本文引用: 1]
Regularity and stability of coupled plate equations with indirect structural or Kelvin-Voigt damping
Stability of an abstract system of coupled hyperbolic and parabolic equations
DOI:10.1007/s00033-012-0274-0 URL [本文引用: 1]
Regularity analysis for an abstract system of coupled hyperbolic and parabolic equations
DOI:10.1016/j.jde.2015.06.010 URL [本文引用: 1]
On the mathematical model for linear elastic systems with analytic damping
DOI:10.1137/0326041 URL [本文引用: 1]
Holomorphic property and exponential stability of the semigroup associated with linear elastic systems with damping
Frequency domain approach for the polynomial stability of a system of partially damped wave equations
DOI:10.1016/j.jmaa.2007.02.021 URL [本文引用: 2]
Characterization of polynomial decay rate for the solution of linear evolution equation
DOI:10.1007/s00033-004-3073-4 URL [本文引用: 1]
Polynomial stability of the Rao-Nakra beam with a single internal viscous damping
DOI:10.1016/j.jde.2020.04.030 URL [本文引用: 1]
Stability and regularity of solution to the Timoshenko beam equation with local Kelvin-Voigt damping
DOI:10.1137/17M1146506 URL [本文引用: 1]
Optimal energy decay rate for partially damped systems by spectral compensation
DOI:10.1137/S0363012903437319 URL [本文引用: 2]
Boundary stabilization of coupled plate equations
Exact decay rates for coupled plates with partial fractional damping
On the sensitivity of the transmission of boundary dissipation for strongly coupled and indirectly damped systems of wave equations
A general framework for the study of indirect damping mechanisms in elastic systems
DOI:10.1006/jmaa.1993.1071 URL [本文引用: 3]
Energy decay estimates for some weakly coupled Euler-Bernoulli and wave equations with indirect damping mechanisms
DOI:10.3934/mcrf.2012.2.45 URL [本文引用: 1]
An analytical method for prediction of the damping in symmetric balanced laminated composites
DOI:10.1002/pc.v20:2 URL [本文引用: 1]
Decay of solutions of the system of thermoelasticity of type III
DOI:10.1142/S0219199703000896
URL
[本文引用: 1]

This paper is devoted to analyzing the long time behavior of solutions of the system of thermoelasticity of type III in a bounded domain of ℝn (n = 1,2,3) and in the whole space ℝn. For the first case, we introduce a decoupled system that allows to reduce the problem of the asymptotic behavior for the original system to a suitable observability inequality for the Lamé system. In this way most of the existing results for the classical system of thermoelasticity are shown to hold for this system too. In particular, we show that: (1) For most domains the energy of the system does not decay uniformly; (2) Under suitable conditions on the domain that may be described in terms of Geometric Optics, the energy of the system decays exponentially; and (3) For most domains in two space dimensions, the energy of smooth solutions decays polynomially. For the problem in the whole space ℝn, first, based on Fourier analysis and Lyapunov's second method, we show that the energy of longitudinal and thermal waves of the system decays as that of the classical heat equation (while that of the transversal wave component is conservative). Then, by means of a careful spectral analysis, we give a sharp description on the decay rate of the high frequency longitudinal and thermal waves of the system.
Long-Time behavior of a coupled heat-wave system arising in fluid-structure interaction
DOI:10.1007/s00205-006-0020-x URL [本文引用: 1]
Stabilization of the weakly coupled plate equations with a locally distributed damping