数学物理学报, 2023, 43(6): 1667-1680

具有尖点环的非光滑微分系统的极限环分支

杨纪华,*, 马亮

宁夏师范学院数学与计算机科学学院 宁夏固原 756000

Limit Cycle Bifurcations of a Non-smooth Differential System with a Cuspidal Loop

Yang Jihua,*, Ma Liang

School of Mathematics and Computer Science, Ningxia Normal University, Ningxia Guyuan 756000

通讯作者: *杨纪华，E-mail: jihua1113@163.com

收稿日期: 2022-11-22   修回日期: 2023-05-17  

基金资助: 国家自然科学基金(12161069)
宁夏自然科学基金(2022AAC05044)
宁夏高等学校一流学科建设(教育学学科)(NXYLXK2021B10)

Received: 2022-11-22   Revised: 2023-05-17  

Fund supported: NSFC(12161069)
Natural Science Foundation of Ningxia(2022AAC05044)
Construction of First-class Disciplines of Higher Education of Ningxia (pedagogy)(NXYLXK2021B10)

摘要

研究具有尖点环的非光滑微分系统在 $n$ 次多项式非光滑扰动下的极限环分支问题. 首先把扰动微分系统的一阶 Melnikov 函数 $M(h)$ 表示成几个具有多项式系数的生成积分的线性组合, 并用数学归纳法证明这些多项式的系数是相互独立的常数. 然后应用 $M(h)$ 的渐近展式得到从原点和尖点环附近分支出极限环个数的下界.

关键词： 极限环; Melnikov 函数; 尖点环; 渐近展式

Abstract

This paper studies the limit cycle bifurcation problem of a non-smooth differential system with a cuspidal loop under non-smooth perturbation of polynomials of degree $n$. Firstly, the first order Melnikov function $M(h)$ of the perturbed differential system is expressed as a linear combination of several generating integrals with polynomial coefficients, and the independence of coefficients of these polynomials is proved by mathematical induction. Then the lower bounds of the number of limit cycles bifurcating the origin and cuspidal loop are obtained by using the asymptotic expansions of $M(h)$.

Keywords： Limit cycle; Melnikov function; Cuspidal loop; Asymptotic expansion

PDF (591KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杨纪华, 马亮. 具有尖点环的非光滑微分系统的极限环分支[J]. 数学物理学报, 2023, 43(6): 1667-1680

Yang Jihua, Ma Liang. Limit Cycle Bifurcations of a Non-smooth Differential System with a Cuspidal Loop[J]. Acta Mathematica Scientia, 2023, 43(6): 1667-1680

1 引言

缓慢变化后的突发行为普遍存在于自然和人工系统中, 通常由非光滑的数学模型来描述, 如机械工程中的碰撞振动系统、含有可控开关的电路系统、神经网络等[1⇓-3]. 因此, 这方面的研究倍受非线性科学界的关注. 非光滑系统不仅可以产生经典的分支 (如 Hopf 分支、极限环分支、同宿轨分支、异宿轨分支等), 而且会产生只有非光滑系统才能具有的更复杂的分支, 如边界碰撞分支[4,5]、擦边分支[6] 等. 在过去的几十年中, 人们对推广光滑系统的经典分支方法来研究非光滑系统做出了许多贡献. 例如, Kukučka 研究了非光滑系统中同宿解的存在性问题, 并证明了扰动系统中存在同宿解[7]. Li 和 Huang 研究了一类平面扰动非光滑 Filippov 系统的同宿轨分支和 Hopf 分支[8].

如果一个系统对由直线或曲线分割的两个或多个不同区域中的连续向量场有不同的定义, 则称该系统为切换系统. 切换系统是一类非光滑系统. 本文主要研究切换系统的极限环分支问题. 据我们所知, 研究这个问题主要有三种方法: 广义 Melnikov 函数法、广义平均法和计算李亚普诺夫常数法. 例如, 文献 [9] 给出了相应的广义一阶 Melnikov 函数公式. 应用这些方法, Llibre 等证明从三次等时多项式系统的周期轨分支出 12 个极限环[10]. Li等[11] 构造了一个具有 15 个极限环的切换立方系统. Guo 等[12] 构造了三次切换系统, 并证明该系统存在 18 个从中心分支的小振幅极限环. 这是在这种三次切换系统中获得的小振幅极限环最大数目的一个最新的下限. 文献 [13] 利用 Melnikov 函数方法, 通过扰动具有广义同宿或双同宿环的分段哈密尔顿系统来考虑同宿分轨支问题. 文献 [14] 也用这种方法给出了切换微分系统中同宿环附近极限环个数的一些充分条件. 文献 [15] 通过扰动具有尖点和幂零鞍点的广义异宿环的分段三次多项式系统, 研究一类 $n$ 次非光滑微分多项式系统极限环个数的下界问题.

本文考虑下面非光滑扰动微分系统

$\begin{aligned} \begin{cases} \dot{x} = y+\varepsilon f^+(x,y), \\ \dot{y} = -x^2+2x-1+\varepsilon g^+(x,y),\\ \end{cases} x\geq0,\quad \begin{cases} \dot{x} = \frac{3}{4}y+\varepsilon f^-(x,y), \\ \dot{y} = 4x^3-2x+\varepsilon g^-(x,y),\\ \end{cases} x<0, \end{aligned}$

其中

$f^\pm(x,y)=\sum\limits_{i+j=0}^na^\pm_{i,j}x^iy^j,\quad g^\pm(x,y)=\sum\limits_{i+j=0}^nb^\pm_{i,j}x^iy^j,\quad i,j,n\in\mathbf{N}.$

当 $\varepsilon=0$ 时, 系统 (1.1) 的哈密尔顿函数为

$H^+(x,y)=\frac{1}{2}y^2+\frac{1}{3}x^3-x^2+x,\ \ x\geq0$

和

$H^-(x,y)=\frac{3}{8}y^2-x^4+x^2,\ \ x<0.$

当 $\varepsilon=0$ 时, 系统 (1.1) 有一族分段光滑的周期轨

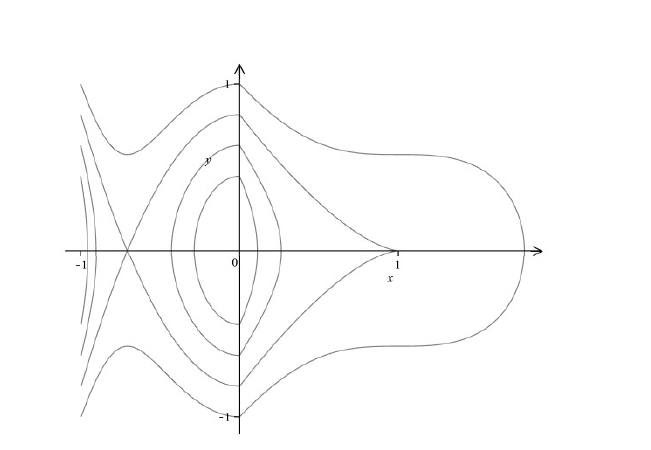
$\Gamma_h=\{(x,y)|H^+(x,y)=h,x\geq0\}\cup\{(x,y)|H^-(x,y)=\widetilde{h},x<0\} \triangleq\Gamma^+_h\cup\Gamma^-_h,$

其中 $\widetilde{h}=\frac{3}{4}h$, $h\in(0,\frac{1}{3})$. 当 $h\rightarrow0$ 时, $\Gamma_h$ 趋于原点; 当 $h\rightarrow\frac{1}{3}$ 时, $\Gamma_h$ 趋于过尖点 $(1,0)$ 和鞍点 $(-\frac{\sqrt{2}}{2},0)$ 的尖点环, 见图1.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   当 $\varepsilon=0$ 时, 系统 (1.1) 的相图


本文主要研究系统 (1.1) 极限环个数的下界问题. 我们首先得到系统 (1.1) 的一阶 Melnikov 函数 $M(h)$ 的代数结构, 即 $M(h)$ 可以表示成几个具有多项式系数的生成积分的线性组合, 并用数学归纳法证明这些多项式的系数是相互独立的, 这是证明这些系数相互独立的一个比较简单的方法. 最后根据 $M(h)$ 的渐近展式得到系统 (1.1) 在原点和尖点环附近的极限环个数.

2 Melnikov 函数的代数结构

由文献 [9] 知系统 (1.1) 有分支函数 $F(h,\varepsilon)=M(h)+O(\varepsilon)$, 其中

$M(h)=\int_{\Gamma^+_h}g^+(x,y){\rm d}x-f^+(x,y){\rm d}y +\frac{4}{3}\int_{\Gamma^-_h}g^-(x,y){\rm d}x-f^-(x,y){\rm d}y,\ h\in(0,\frac{1}{3})$

是系统 (1.1) 的一阶 Melnikov 函数. 如果 $M(h)t\equiv0$, $h\in(0,\frac{1}{3})$, 则当 $|\varepsilon|$ 充分小时, 从系统 (1.1) 的未扰动系统的周期环域中分支出极限环的个数不超过它在 $(0,\frac{1}{3})$ 中孤立零点的个数, 并且 $M(h)$ 孤立零点的个数提供了系统 (1.1) 极限环个数的一个下界, 见文献 [9,16]. 为了方便, 记

$I_{i,j}(h)=\int_{\Gamma^+_h}x^iy^j{\rm d}y,\ J_{i,j}(h)=\int_{\Gamma^-_h}x^iy^j{\rm d}y,\ h\in(0,\frac{1}{3}).$

因为轨道 $\Gamma^\pm_h$ 关于 $x$ 轴对称, 所以 $I_{i,2j+1}(h)=J_{i,2j+1}(h)\equiv0$. 我们首先证明下面引理.

引理 2.1 当 $h\in(0,\frac{1}{3})$ 时,

$M(h)=\Big(\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha^+_ih^i\Big) I_{0,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-1}{2}]}\beta^+_ih^i\Big) I_{1,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-2}{2}]}\gamma^+_ih^i\Big) I_{2,0}(h)\\ +\Big(\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha^-_ih^i\Big) J_{0,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-1}{2}]}\beta^-_ih^i\Big)J_{1,0}(h)\\ +\Big(\sum\limits_{i=0}^{[\frac{n-2}{2}]}\gamma^-_ih^i\Big) J_{2,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-3}{2}]}\delta^-_ih^i\Big)J_{3,0}(h),$

其中 $\alpha^\pm_i(0\leq i\leq[\frac{n}{2}])$, $\beta^\pm_i(0\leq i\leq[\frac{n-1}{2}])$, $\gamma^\pm_i(0\leq i\leq[\frac{n-2}{2}])$ 和 $\delta^-_i(0\leq i\leq[\frac{n-3}{2}])$ 是可以由 $a^\pm_{i,j}$ 和 $b^\pm_{i,j}$ 表示的常数, 且它们是相互独立的.

证 由格林公式可得

$\int_{\Gamma^+_{h}}x^iy^j{\rm d}x =-\frac{j}{i+1}\int_{\Gamma^+_{h}}x^{i+1}y^{j-1}{\rm d}y,$
$\int_{\Gamma^-_{h}}x^iy^j{\rm d}x =-\frac{j}{i+1}\int_{\Gamma^-_{h}}x^{i+1}y^{j-1}{\rm d}y.$

由 (2.1)、(2.3) 和 (2.4) 式可得

$M(h)=-\sum\limits_{i+j=1,j\geq 1}^n\frac{j}{i+1}b^+_{i,j}\int_{\Gamma^+_h}x^{i+1}y^{j-1}{\rm d}y -\sum\limits_{i+j=0}^na^+_{i,j}\int_{\Gamma_h^+}x^iy^j{\rm d}y\\ -\sum\limits_{i+j=1,j\geq 1}^n\frac{4j}{3(i+1)}b^-_{i,j}\int_{\Gamma^-_h}x^{i+1}y^{j-1}{\rm d}y -\sum\limits_{i+j=0}^n\frac{4}{3}a^-_{i,j}\int_{\Gamma_h^-}x^iy^j{\rm d}y\\ \triangleq \sum\limits_{i+j=0}^n\xi_{i,j}I_{i,j}(h)+ \sum\limits_{i+j=0}^n\eta_{i,j}J_{i,j}(h),$

其中

$\xi_{i,j}=\begin{cases} -a^+_{i,j}-\frac{j+1}{i}b^+_{i-1,j+1},\ 1\leq i\leq n,1\leq i+j\leq n,\\ -a^+_{i,j},\qquad\qquad\qquad \ i=0,0\leq j\leq n, \end{cases}\\ \eta_{i,j}=\begin{cases} -\frac{4}{3}a^+_{i,j}-\frac{4(j+1)}{3i}b^+_{i-1,j+1},\ 1\leq i\leq n,1\leq i+j\leq n,\\ -\frac{4}{3}a^+_{i,j},\qquad\qquad\qquad\quad \ i=0,0\leq j\leq n. \end{cases}$

显然, $\xi_{i,j}$ 和 $\eta_{i,j}$ 是可以任意选取的常数. 我们断言

$\sum\limits_{i+j=0}^n\xi_{i,j}I_{i,j}(h)=\Big(\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha^+_ih^i\Big) I_{0,0}(h)+\Big(\sum\limits_{j=0}^{[\frac{n-1}{2}]}\beta^+_jh^j\Big) I_{1,0}(h)+\Big(\sum\limits_{k=0}^{[\frac{n-2}{2}]}\gamma^+_kh^k\Big) I_{2,0}(h),$

且 $\alpha^+_i\ (i=0,1,2,\cdots,[\frac{n}{2}])$, $\beta^+_j\ (j=0,1,2,\cdots,[\frac{n-1}{2}])$ 和 $\gamma^+_k$ $(k=0,1,2,\cdots,[\frac{n-2}{2}])$ 是相互独立的. 事实上, 在 $H^+(x,y)=h$ 中把 $x$ 看做 $y$ 和 $h$ 的函数, 两端同时关于 $y$ 求偏导数可得

$y+x^2\frac{\partial x}{\partial y}-2x\frac{\partial x}{\partial y}+\frac{\partial x}{\partial y}=0.$

(2.6) 式两端同乘以 $x^{i}y^{j-1}{\rm d}y$ 并沿着 $\Gamma_h^+$ 积分可得

$I_{i,j}(h)=\frac{j-1}{i+3}I_{i+3,j-2}(h)+\frac{j-1}{i+1}I_{i+1,j-2}(h)-\frac{2(j-1)}{i+2}I_{i+2,j-2}(h), \ i\geq0,\ j\geq2.$

类似地, $H^+(x,y)=h$ 两端同乘以 $x^{i-3}y^{j}{\rm d}y$ 并沿着 $\Gamma_h^+$ 积分可得

$I_{i,j}(h)=3hI_{i-3,j}(h)-\frac{3}{2}I_{i-3,j+2}(h)+3I_{i-1,j}(h)-3I_{i-2,j}(h),\ i\geq3,\ j\geq0.$

于是利用 (2.7) 和 (2.8) 式得到

$I_{i,j}(h)=\frac{6i}{2i+3j+3}\Big[hI_{i-3,j}(h)+\frac{i+j}{i-1}I_{i-1,j}(h)-\frac{2i+j-3}{2(i-2)}I_{i-2,j}(h)\Big], i\geq3, j\geq0,$
$I_{i,j}(h)=\frac{2(j-1)}{2i+3j+3}\Big[3hI_{i,j-2}(h)-\frac{2i}{i+1}I_{i+1,j-2}(h)+\frac{i}{i+2}I_{i+2,j-2}(h)\Big], i\geq0,j\geq2.$

下面用数学归纳法证明断言. 由 (2.9) 和 (2.10) 式得

$\begin{cases} I_{0,2}(h)=\frac{2}{3}hI_{0,0}(h),\\ I_{3,0}(h)=2hI_{0,0}(h)-3I_{1,0}(h)+3I_{2,0}(h),\\ I_{1,2}(h)=\frac{4}{33}hI_{0,0}(h)+\frac{2}{11}(3h-1)I_{1,0}(h).\end{cases}$

于是, 当 $n=2,3$ 时有

$\sum\limits_{i+j=0}^2\xi_{i,j}I_{i,j}(h)=\ \big(\frac{2}{3}h\xi_{0,2} +\xi_{0,0}\big)I_{0,0}(h)+\xi_{1,0}I_{1,0}(h)+\xi_{2,0}I_{2,0}(h),\\ \sum\limits_{i+j=0}^3\xi_{i,j}I_{i,j}(h)=\ \big[\big(\frac{2}{3}\xi_{0,2}+\frac{4}{33}\xi_{1,2} +2\xi_{3,0}\big)h+\xi_{0,0}\big]I_{0,0}(h)\\ +\big(\frac{6}{11}\xi_{1,2}h+\xi_{1,0}-\frac{2}{11}\xi_{1,2}-3\xi_{3,0}\big)I_{1,0}(h)+(\xi_{2,0}+3\xi_{3,0})I_{2,0}(h).$

所以, 当 $n=2,3$ 时断言成立. 假设当 $i+j\leq k-1$ ($k\geq4$) 时断言成立. 设 $k$ 是偶数 (如果 $k$ 是奇数, 可类似地证明), 在 (2.10) 式中取 $(i,j)=(0,k),(2,k-2),\cdots,(k-2,2)$, 在 (2.9) 式中取 $(i,j)=(k,0)$, 得到

$\mathbf{\Phi}\left(\begin{matrix} I_{0,k}(h)\\ I_{2,k-2}(h)\\ I_{4,k-4}(h)\\ \vdots\\ I_{k-2,2}(h)\\ I_{k,0}(h) \end{matrix}\right)=\left(\begin{matrix} \frac{2(k-1)}{k+1}hI_{0,k-2}(h)\\ \frac{2(k-3)}{3k+1}\big(3hI_{2,k-4}(h)-\frac{4}{3}I_{3,k-4}(h)\big)\\ \frac{2(k-5)}{3k-1}\big(3hI_{4,k-6}(h)-\frac{8}{5}I_{5,k-6}(h)\big)\\ \vdots\\ \frac{2}{2k+5}\big(3hI_{k-2,0}(h)-\frac{2(k-2)}{n-1}I_{k-1,0}(h)\big)\\ \frac{2k}{2k+3}\big(3hI_{k-3,0}(h)+\frac{3k}{k-1}I_{k-1,0}(h)-\frac{3(2k-3)}{2k-4}I_{k-2,0}(h)\big) \end{matrix}\right),$

其中

$\mathbf{\Phi}=\left(\begin{matrix} 1&~0~&0&0&\cdots&0&0\\ 0&1&~\frac{3-k}{3k+1}~&0&\cdots&~0~&0\\ 0&0&1&\frac{4(5-k)}{3(3k-1)} \cdots&0&0\\ \vdots \vdots \vdots \vdots \vdots \vdots \vdots\\ 0&0&0&0&\cdots&1&\frac{2(2-k)}{k(2k+5)}\\ 0&0&0&0&\cdots&0&1 \end{matrix}\right).$

直接计算可得行列式 $|\Phi|=1$. 所以, 当 $n=k$ ($k$ 是偶数) 时, 由归纳假设和 (2.12) 式可得

$\sum\limits_{i+j=0}^n\xi_{i,j}I_{i,j}(h)=\Big(\sum\limits_{i=0}^{[\frac{n-1}{2}]}\tilde{\alpha}^+_ih^i\Big) I_{0,0}(h)+\Big(\sum\limits_{j=0}^{[\frac{n-2}{2}]}\tilde{\beta}^+_jh^j\Big) I_{1,0}(h)+\Big(\sum\limits_{k=0}^{[\frac{n-3}{2}]}\tilde{\gamma}^+_kh^k\Big) I_{2,0}(h)\\+\xi_{0,n}\frac{2(n-1)}{n+1}hI_{0,n-2}(h)+\xi_{2,n-2} \frac{2(n-3)}{3n+1}\big(3hI_{2,n-4}(h)-\frac{4}{3}I_{3,n-4}(h)\big)\\+\cdots+\xi_{n,0}\frac{2n}{2n+3}\big(3hI_{n-3,0}(h)+\frac{3n}{n-1}I_{n-1,0}(h)-\frac{3(2n-3)}{2n-4}I_{n-2,0}(h)\big)\\ \triangleq \Big(\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha^+_ih^i\Big) I_{0,0}(h)+\Big(\sum\limits_{j=0}^{[\frac{n-1}{2}]}\beta^+_jh^j\Big) I_{1,0}(h)+\Big(\sum\limits_{k=0}^{[\frac{n-2}{2}]}\gamma^+_kh^k\Big) I_{2,0}(h),$

其中 $\tilde{\alpha}^+_i$, $\tilde{\beta}^+_i$ 和 $\tilde{\gamma}^+_i$ 是常数. 所以, 当 $n=k$ 时 (2.5) 式成立.

下面证明 $\alpha^+_i$ $(i=0,1,2,\cdots,[\frac{n}{2}])$, $\beta^+_j$ $(j=0,1,2,\cdots,[\frac{n-1}{2}])$ 和 $\gamma^+_k$ $(k=0,1,2,\cdots,[\frac{n-2}{2}])$ 的独立性. 事实上, 由归纳假设知, $\tilde{\alpha}^+_i$ $(i=0,1,2,\cdots,[\frac{n-1}{2}])$, $\tilde{\beta}^+_j$ $(j=0,1,2,\cdots,[\frac{n-2}{2}])$ 和 $\tilde{\gamma}^+_k$ $(k=0,1,2,\cdots,[\frac{n-3}{2}])$ 是相互独立的, 即可得雅克比矩阵

$\mathbf{A}=\frac{\partial\Big(\tilde{\alpha}^+_{[\frac{n-1}{2}]},\cdots,\tilde{\alpha}^+_0,\tilde{\beta}^+_{[\frac{n-2}{2}]},\cdots,\tilde{\beta}^+_0, \tilde{\gamma}^+_{[\frac{n-3}{2}]},\cdots,\tilde{\gamma}^+_0\Big)} {\partial\Big(\xi_{i_0,j_{[\frac{n-1}{2}]}},\cdots,\xi_{i_{[\frac{n-1}{2}]},j_0}, \xi_{k_0,l_{[\frac{n-2}{2}]}},\cdots,\xi_{k_{[\frac{n-2}{2}]},l_0}, \xi_{s_0,t_{[\frac{n-3}{2}]}},\cdots,\xi_{s_{[\frac{n-3}{2}]},t_0}\Big)}$

的行列式 $|\mathbf{A}|$ 不等于零, 式中 $\xi_{i,j}$ 的下标之和小于等于 $n-1$. 直接计算得雅可比矩阵

$\mathbf{\Psi}=\frac{\partial\Big(\alpha^+_{[\frac{n-1}{2}]},\cdots,\alpha^+_0,\beta^+_{[\frac{n-2}{2}]},\cdots,\beta^+_0, \gamma^+_{[\frac{n-3}{2}]},\cdots,\gamma^+_0,\alpha^+_{[\frac{n}{2}]},\gamma^+_{[\frac{n-2}{2}]}\Big)} {\partial\Big(\xi_{i_0,j_{[\frac{n-1}{2}]}},\cdots,\xi_{i_{[\frac{n-1}{2}]},j_0}, \xi_{k_0,l_{[\frac{n-2}{2}]}},\cdots,\xi_{k_{[\frac{n-2}{2}]},l_0}, \xi_{s_0,t_{[\frac{n-3}{2}]}},\cdots,\xi_{s_{[\frac{n-3}{2}]},t_0},\xi_{0,n},\xi_{2,n-2}\Big)}\\ =\left(\begin{matrix} \mathbf{A} & \mathbf{B} & \mathbf{C}\\ \mathbf{0} & \ \frac{2^{[\frac{n}{2}]}}{n+1}\ & \sigma\\ \mathbf{0}&0&\nu \end{matrix}\right),$

其中 $\nu=6^{[\frac{n-2}{2}]}\frac{(n-3)!!}{\prod\limits_{k=4}^n(3k+1)}$, $\sigma$ 是一个常数, $\mathbf{0}$ 是行向量, $\mathbf{B}$ 和 $\mathbf{C}$ 都是列向量. 显然

$| \mathbf{\Psi}|=\frac{2^{[\frac{n}{2}]}\nu}{n+1}|\mathbf{A}|\neq0.$

所以, $\alpha^+_i$ $(i=0,1,2,\cdots,[\frac{n}{2}])$, $\beta^+_j$ $(j=0,1,2,\cdots,[\frac{n-1}{2}])$ 和 $\gamma^+_k$ $(k=0,1,2,\cdots,[\frac{n-2}{2}])$ 是相互独立的.

类似地可以证明

$\sum\limits_{i+j=0}^n\eta_{i,j}J_{i,j}(h)=\ \Big(\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha^-_ih^i\Big)J_{0,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-1}{2}]}\beta^-_ih^i\Big)J_{1,0}(h) \\ +\Big(\sum\limits_{i=0}^{[\frac{n-2}{2}]}\gamma^-_ih^i\Big) J_{2,0}(h)+\Big(\sum\limits_{i=0}^{[\frac{n-3}{2}]}\delta^-_ih^i\Big)J_{3,0}(h),$

且 $\alpha^-_i$ $ (0\leq i\leq[\frac{n}{2}])$, $\beta^-_i$ $(0\leq i\leq[\frac{n-1}{2}])$, $\gamma^-_i\ (0\leq i\leq[\frac{n-2}{2}])$ 和 $\delta^-_i(0\leq i\leq[\frac{n-3}{2}])$ 是相互独立的.

综上可得, (2.2) 式成立, 且 $\alpha^\pm_i$ $(0\leq i\leq[\frac{n}{2}])$, $\beta^\pm_i$ $(0\leq i\leq[\frac{n-1}{2}])$, $\gamma^\pm_i$ $(0\leq i\leq[\frac{n-2}{2}])$ 和 $\delta^-_i$ $(0\leq i\leq[\frac{n-3}{2}])$ 是相互独立的. 引理 2.1 得证.

3 主要结果与证明

首先给出一阶 Melnikov 函数 $M(h)$ 在原点和尖点环附近的渐近展式.

引理 3.1 当 $0<h\ll1$ 时, $I_{1,0}(h)$ 和 $I_{2,0}(h)$ 的渐近展式为

$I_{1,0}(h)=\sqrt{h}\sum\limits_{i=1}^{+\infty}A_{1i}h^i, I_{2,0}(h)=\sqrt{h}\sum\limits_{i=1}^{+\infty}A_{2i}h^i,$

其中 $A_{ki}\ (k=1,2;i=1,2,\cdots)$ 是实数.

证 因为 $0<h<\frac{1}{3}$, $-\sqrt{2h}<y<\sqrt{2h}$, 所以 $-1<\frac{3}{2}y^2-3h<0$, 因此可得下面的渐近展开式

$\Big(1+\frac{3}{2}y^2-3h\Big)^\frac{k}{3}=\sum\limits_{i=0}^{+\infty}\mu^k_i\Big(\frac{3}{2}y^2-3h\Big)^i,$

其中

$\mu^k_0=1,\ \mu^k_i=\frac{\frac{k}{3}\big(\frac{k}{3}-1\big)\cdots\big(\frac{k}{3}-i+1\big)}{i!},\ i=1,2,\cdots;\ k=1,2.$

所以, 当 $0<h\ll1$ 时,

$I_{2,0}(h)=2\int_0^{-\sqrt{2h}}\Big[1-\Big(1+\frac{3}{2}y^2-3h\Big)^\frac{1}{3}\Big]^2{\rm d}y\\ =-2\sqrt{2h}+2\sum\limits_{i=0}^{+\infty}(\mu^2_i-2\mu^1_i)\int_0^{-\sqrt{2h}}\Big(\frac{3}{2}y^2-3h\Big)^i{\rm d}y\\ =\sqrt{h}\sum\limits_{i=1}^{+\infty}A_{2i}h^i,$

其中

$A_{2i}=-2\sqrt{2}3^i(\mu^2_i-2\mu^1_i)\int_0^1(t^2-1)^i{\rm d}t,\ i=1,2,\cdots.$

类似地可得 $I_{1,0}(h)$ 的渐近展式, 且

$A_{1i}=-2\sqrt{2}3^i\mu^1_i\int_0^1(t^2-1)^i{\rm d}t,\ i=1,2,\cdots.$

证毕.

引理 3.2 当 $0<h\ll1$ 时, $J_{1,0}(h)$, $J_{2,0}(h)$ 和 $J_{3,0}(h)$ 的渐近展式为

$J_{1,0}(h)=\sum\limits_{j=0}^{+\infty}B_{1j}h^{j+1},\\ J_{2,0}(h)=\sqrt{h}\sum\limits_{j=0}^{+\infty}B_{2j}h^{j+1},\\ J_{3,0}(h)=\sum\limits_{j=0}^{+\infty}B_{3j}h^{j+2},$

其中 $B_{kj}\ (k=1,2,3;j=0,1,2,\cdots)$ 是实数.

证 方程 $H^-(x,y)=\frac{3}{4}h$ 可以写成

$x^2-x^4=z^2,\ x<0,$

其中 $z^2=\frac{3}{4}h-\frac{3}{8}y^2$, $z>0$. 易知, 当 $0<-x\ll1$ 时, 方程 (3.3) 存在唯一的 $C^\infty$ 函数

$x=\phi(z)=-z+O(z^3)=\sum\limits_{j=0}^{+\infty}\kappa_{1j}z^{2j+1},$

其中 $\kappa_{10}=-1,\ \kappa_{11}=\frac{1}{2}, \ \kappa_{12}=-\frac{7}{8},\ \kappa_{13}=\frac{33}{16},\ \kappa_{14}=-\frac{715}{128},\cdots.$ 所以, 当 $0<h\ll1$ 时,

$J_{1,0}(h)=2\sum\limits_{j=0}^{+\infty}\kappa_{1j}\int_{0}^{\sqrt{2h}}\Big(\frac{3}{4}h-\frac{3}{8}y^2\Big)^{j+\frac{1}{2}}{\rm d}y =\sum\limits_{j=0}^{+\infty}B_{1j}h^{j+1},$

其中 $\kappa_{1j}$ 是实数, $B_{1j}=2^{-2j+\frac{1}{2}}3^{j+\frac{1}{2}}\kappa_{1j}\int_0^1(1-t^2)^{j+\frac{1}{2}}{\rm d}t,\ j=0,1,2,\cdots$.

$J_{2,0}(h) =2\sum\limits_{j=1}^{+\infty}\kappa_{2j}\int_{0}^{\sqrt{2h}}\Big(\frac{3}{4}h-\frac{3}{8}y^2\Big)^{j}{\rm d}y =\sqrt{h}\sum\limits_{j=0}^{+\infty}B_{2j}h^{j+1},$

其中 $\kappa_{2j}$ 是实数, $B_{2j}=2^{-2j-\frac{1}{2}}3^{j}\kappa_{2,j+1}\int_0^1(1-t^2)^{j+1}{\rm d}t,\ j=0,1,2,\cdots$.

$J_{3,0}(h) =2\sum\limits_{j=1}^{+\infty}\kappa_{3j}\int_{0}^{\sqrt{2h}}\Big(\frac{3}{4}h-\frac{3}{8}y^2\Big)^{j+\frac{1}{2}}{\rm d}y =\sum\limits_{j=0}^{+\infty}B_{3j}h^{j+2},$

其中 $\kappa_{3j}$ 是实数, $B_{3j}=2^{-2j-\frac{3}{2}}3^{j+\frac{3}{2}}\kappa_{3,j+1}\int_0^1(1-t^2)^{j+\frac{3}{2}}{\rm d}t,\ j=0,1,2,\cdots$.

引理 3.3 当 $0<\frac{1}{3}-h\ll1$ 时, $I_{1,0}(h)$ 和 $I_{2,0}(h)$ 可展开为

$I_{0,0}(h)=\sum_{k=0}^{+\infty}\rho_{0k}|u|^k,\\ I_{1,0}(h)=\rho_1|u|^\frac{5}{6}+\sum_{k=0}^{+\infty}\rho_{1k}|u|^k,\\ I_{2,0}(h)=\rho_2|u|^\frac{7}{6}+\sum_{k=0}^{+\infty}\rho_{2k}|u|^k,$

其中 $u=h-\frac{1}{3}$, $\rho_1$, $\rho_2$, $\rho_{0k}$, $\rho_{1k}$ 和 $\rho_{2k}\ (k\geq0)$ 是实数.

证 注意到下面的渐近展开式

$(1+x)^\frac{1}{2}=\sum_{k=0}^{+\infty}\lambda^1_kx^k,\ \ x\in[-1,1],$

其中 $\lambda^1_0=1,\lambda^1_k=\frac{\frac{1}{2}(\frac{1}{2}-1)\cdots(\frac{1}{2}-k+1)}{k!},k\geq1$. 即可得 $I_{0,0}(h)$ 的渐近展式. 下面计算 $I_{1,0}(h)$ 和 $I_{2,0}(h)$ 的渐近展式. 计算可得

$I_{1,0}(h)=-2\sqrt{2}\int_0^{\sqrt[3]{3h-1}+1}\sqrt{h-\frac{1}{3}-\frac{1}{3}(x-1)^3}{\rm d}x.$

令 $x=\sqrt[3]{3}t+1$, $u=h-\frac{1}{3}$, 则 (3.6) 式可化为

$I_{1,0}(h)=-2\sqrt{2}\sqrt[3]{3}\int_{-\frac{1}{\sqrt[3]{3}}}^{\sqrt[3]{h-\frac{1}{3}}}\sqrt{h-\frac{1}{3}-t^3}{\rm d}t\\ =-2\sqrt{2}\sqrt[3]{3}\int_{-\frac{1}{\sqrt[3]{3}}}^{\sqrt[3]{u}}(-t)^\frac{3}{2}\sqrt{1+(-t)^{-3}u}{\rm d}t.$

容易验证 $-1<(-t)^{-3}u<0$, 由 (3.5) 式可得

$I_{1,0}(h)=-2\sqrt{2}\sqrt[3]{3}\int_{-\frac{1}{\sqrt[3]{3}}}^{\sqrt[3]{u}}(-t)^\frac{3}{2}\sum_{k=0}^{+\infty}\lambda^1_k(-t^{-3}u)^k{\rm d}t\\ =-2\sqrt{2}\sqrt[3]{3}\sum_{k=0}^{+\infty}\lambda^1_ku^k\int_{-\frac{1}{\sqrt[3]{3}}}^{\sqrt[3]{u}}(-t)^{\frac{3}{2}-3k}{\rm d}t\\ =4\sqrt{2}\sqrt[3]{3}\sum_{k=0}^{+\infty}\frac{(-1)^k\lambda^1_k}{5-6k}|u|^\frac{5}{6}+ 4\sqrt{2}\sum_{k=0}^{+\infty}\frac{(-1)^k3^{k-\frac{1}{2}}\lambda^1_k}{5-6k}|u|^k\\ \triangleq \rho_1|u|^\frac{5}{6}+ \sum_{k=0}^{+\infty}\rho_{1k}|u|^k,$

其中

$\rho_1=4\sqrt{2}\sqrt[3]{3}\sum_{k=0}^{+\infty}\frac{(-1)^k\lambda^1_k}{5-6k},\ \rho_{1k}=4\sqrt{2}\frac{(-1)^k3^{k-\frac{1}{2}}\lambda^1_k}{5-6k},\ k=0,1,2,\cdots.$

$I_{2,0}(h)$ 的渐近展式可类似地得到.

注 3.1 由正项级数的拉贝判别法可知级数 $\sum\limits_{k=0}^{+\infty}\frac{(-1)^k\lambda^1_k}{5-6k}$ 绝对收敛.

引理 3.4 当 $0<\frac{1}{3}-h\ll1$ 时, $J_{1,0}(h)$, $J_{2,0}(h)$ 和 $J_{3,0}(h)$ 的渐近展式为

$J_{0,0}(h)=\sum_{i=0}^{+\infty}\sigma_{0i}|u|^i,\\ J_{1,0}(h)=\sum_{i=1}^{+\infty}\varsigma_{1i}|u|^i\ln|u|+\sigma_1+\sum_{i=0}^{+\infty}\sigma_{1i}|u|^{1+\frac{i}{2}},\\ J_{2,0}(h)=\sigma_2|u|\ln|u|+\sum_{i=0}^{+\infty}\sigma_{2i}|u|^i,\\ J_{3,0}(h)=\sum_{i=1}^{+\infty}\varsigma_{3i}|u|^i\ln|u|+\sigma_3+\sum_{i=0}^{+\infty}\sigma_{3i}|u|^{1+\frac{i}{2}},$

其中 $u=h-\frac{1}{3}$, $\sigma_1$, $\sigma_2$, $\sigma_3$, $\sigma_{0i}$, $\sigma_{1i}$, $\sigma_{2i}$, $\sigma_{3i}$, $\varsigma_{1i}$ 和 $\varsigma_{3i}$ 是实数.

证 类似于 $I_{0,0}(h)$ 可得 $J_{0,0}(h)$ 的展式. 下面计算 $J_{1,0}(h)$、$J_{2,0}(h)$ 和 $J_{3,0}(h)$ 的渐近展式. 直接计算可得

$J_{1,0}(h)= 2\sqrt{2}\int_0^{-\sqrt{\frac{1-\sqrt{1-3h}}{2}}}\sqrt{h-\frac{1}{3}+\frac{4}{3}(x^2-\frac{1}{2})^2}{\rm d}x.$

令 $x^2=\frac{\sqrt{3}}{2}t+\frac{1}{2}$, $u=h-\frac{1}{3}$, 则 (3.10) 式可化为

$J_{1,0}(h)=2\sqrt{6}\int_{-\frac{1}{\sqrt{3}}}^{-\sqrt{|u|}}\frac{t\sqrt{1+t^{-2}u}}{\sqrt{1+\sqrt{3}t}}{\rm d}t.$

容易验证 $-1<t^{-2}u<0$, $-1<\sqrt{3}t<0$, 并注意到下面的渐近展开式

$(1+x)^{-\frac{1}{2}}=\sum_{k=0}^{+\infty}\lambda^2_kx^k,\ \ x\in(-1,1],$

其中

$\lambda^2_0=1,\ \lambda^2_k=\frac{-\frac{1}{2}(-\frac{1}{2}-1)\cdots(-\frac{1}{2}-k+1)}{k!},k\geq1.$

由 (3.5)、(3.11) 和 (3.12) 式可得

$J_{1,0}(h)=2\sqrt{6}\int_{-\frac{1}{\sqrt{3}}}^{-\sqrt{|u|}}t\Big(\sum_{k=0}^{+\infty}\lambda^1_k(t^{-2}u)^k\Big)\Big(\sum_{k=0}^{+\infty}\lambda^2_k(\sqrt{3}t)^k\Big){\rm d}t\\ =2\sqrt{2}\sum_{i=0}^{+\infty}\Big(\lambda^1_iu^i\sum_{j=0}^{+\infty}3^\frac{j+1}{2}\lambda_j^2\int_{-\frac{1}{\sqrt{3}}}^{-\sqrt{|u|}}t^{j-2i+1}{\rm d}t\Big)\\ =2\sqrt{2}\sum_{i=1}^{+\infty}(-1)^i3^{i-\frac{1}{2}}\lambda^1_i\lambda_{2i-2}^2|u|^i\ln\sqrt{3|u|}\\ +2\sqrt{2}\sum_{i=0}^{+\infty}\sum_{\substack{j=0,\\j\neq 2i-2}}^{+\infty}\frac{(-1)^{i+j}3^\frac{j+1}{2}\lambda^1_i\lambda^2_j}{j-2i+2}\Big(|u|^{1+\frac{j}{2}}-3^{i-\frac{j}{2}-1}|u|^i\Big)\\ =\sum_{i=1}^{+\infty}\sigma_{0i}|u|^i\ln|u|+\sigma_1+\sum_{i=0}^{+\infty}\sigma_{1i}|u|^{1+\frac{i}{2}},$

其中

$\sigma_{0i}=(-1)^i\sqrt{2}\ln3\, 3^{i-\frac{1}{2}}\lambda^1_i\lambda_{2i-2}^2,\ \ \sigma_1=\sum_{j=0}^{+\infty}\frac{3^{-\frac{1}{2}}(-1)^{j+1}\lambda^1_0\lambda^2_j}{j+2},\\ \sigma_{1i}=\begin{cases} \sum\limits_{\substack{j=0\\j\neq\frac{i}{2}+1}}^{+\infty}\frac{(-1)^j3^{\frac{i+1}{2}}\lambda^1_j\lambda^2_i}{i-2j+2}+ \sum\limits_{\substack{j=0\\j\neq i}}^{+\infty}\frac{(-1)^{\frac{i}{2}+j}3^{\frac{i+1}{2}}\lambda^1_{\frac{i}{2}+1}\lambda^2_j}{j-i}, \ i\ {是偶数},\\ \sum\limits_{j=0}^{+\infty}\frac{(-1)^{j+1}3^\frac{i+1}{2}\lambda^1_j\lambda^2_i}{i-2j+2},\qquad\qquad\qquad\qquad\qquad \quad\ i\ {是奇数}. \end{cases}$

证毕.

注 3.2 对固定的自然数 $i$, 由正项级数的拉贝判别法可知 $\sigma_1$ 中的级数以及 $\sigma_{1i}$ 中出现的三个数项级数都是绝对收敛的.

下面的引理 3.5 可以由牛顿二项式定理直接得到.

引理 3.5 当 $0<\frac{1}{3}-h\ll1$ 时, 可得下面的渐近展式

$\sum\limits_{i=0}^{[\frac{n}{2}]}\alpha_i^\pm h^i=\sum_{i=0}^{[\frac{n}{2}]}a_i^\pm |u|^i,\quad\ \ \sum\limits_{i=0}^{[\frac{n-1}{2}]}\beta_i^\pm h^i=\sum_{i=0}^{[\frac{n-1}{2}]}b_i^\pm |u|^i,\\ \sum\limits_{i=0}^{[\frac{n-2}{2}]}\gamma_i^\pm h^i=\sum_{i=0}^{[\frac{n-2}{2}]}c_i^\pm |u|^i,\ \ \sum\limits_{i=0}^{[\frac{n-3}{2}]}\delta_i^- h^i=\sum_{i=0}^{[\frac{n-3}{2}]}d_i^- |u|^i,$

其中 $u=h-\frac{1}{3}$, $a_i^\pm\ (i=0,1,2,\cdots,[\frac{n}{2}])$, $b_i^\pm\ (i=0,1,2,\cdots,[\frac{n-1}{2}])$, $c_i^\pm$ $ (i=0,1,2,\cdots,[\frac{n-2}{2}])$ 和 $d_i^-\ (i=0,1,2,\cdots,[\frac{n-3}{2}])$ 是相互独立的, 并且

$a_i^\pm=\sum\limits_{k=i}^{[\frac{n}{2}]}\frac{(-1)^i}{3^{k-i}}C_k^i\alpha_i^\pm, \quad \ b_i^\pm=\sum\limits_{k=i}^{[\frac{n-1}{2}]}\frac{(-1)^i}{3^{k-i}}C_k^i\beta_i^\pm,$
$c_i^\pm=\sum\limits_{k=i}^{[\frac{n-2}{2}]}\frac{(-1)^i}{3^{k-i}}C_k^i\delta_i^\pm,\quad \ d_i^-=\sum\limits_{k=i}^{[\frac{n-3}{2}]}\frac{(-1)^i}{3^{k-i}}C_k^i\gamma_i^-.$

命题 3.1 当 $0<h\ll1$ 时, $M(h)$ 的渐近展开式为

$M(h)=\sum\limits_{i=0}^{\infty}c_{1i}h^{i+\frac{1}{2}} +\sum\limits_{i=0}^{\infty}c_{2i}h^{i+1},$

其中 $c_{1i}\ (i=0,1,2,\cdots,[\frac{n}{2}])$ 和 $c_{2i}\ (i=0,1,2,\cdots,[\frac{n-1}{2}])$ 是相互独立的, 并且

$c_{1i}=\begin{cases} \sum\limits_{k=0}^i\beta^+_kA_{1,i-k}+\sum\limits_{k=0}^i\gamma^+_kA_{2,i-k}+\sum\limits_{k=0}^{i-1}\gamma^-_kB_{2,i-1-k}\!+\!2\sqrt{2}\alpha^-_i\!-\!2\sqrt{2}\alpha^+_i,\ 0\leq i\leq[\frac{n}{2}],\\ \sum\limits_{k=0}^{[\frac{n}{2}]}\beta^+_kA_{1,i-k}+\sum\limits_{k=0}^{[\frac{n}{2}]}\gamma^+_kA_{2,i-k}+\sum\limits_{k=0}^{{[\frac{n}{2}]}-1}\gamma^-_kB_{2,i-1-k},\ \qquad \qquad \qquad\qquad i\geq[\frac{n}{2}]+1,\\ \end{cases}\\ c_{2i}=\begin{cases} \sum\limits_{k=0}^i\beta^-_kB_{1,i-k}+\sum\limits_{k=0}^{i-1}\delta^-_kB_{3,i-1-k},\qquad\ 0\leq i\leq[\frac{n-1}{2}],\\ \sum\limits_{k=0}^{[\frac{n-1}{2}]}\beta^-_kB_{1,i-k}+\sum\limits_{k=0}^{{[\frac{n-1}{2}]}-1}\delta^-_kB_{3,i-1-k},\ i\geq[\frac{n-1}{2}]+1.\end{cases}$

证 把 (3.1) 和 (3.2) 式带入 (2.2) 式即可得 (3.15) 式. 下面证明当 $n$ 是偶数时 ($n$ 是奇数时可以类似地证明), $c_{1i}\ (i=0,1,2,\cdots,[\frac{n}{2}])$ 和 $c_{2i}\ (i=0,1,2,\cdots,[\frac{n-1}{2}])$ 是相互独立的.

事实上, 直接计算可得

$A=\frac{\partial(c_{10},c_{11},\cdots,c_{1[\frac{n}{2}]},c_{20},c_{21},\cdots,c_{2[\frac{n-1}{2}]})} {\partial(\alpha^-_0,\alpha^-_1,\cdots,\alpha^-_{[\frac{n}{2}]},\beta^-_0,\beta^-_1,\cdots,\beta^-_{[\frac{n-1}{2}]})}\\ =\left(\begin{matrix} 2\sqrt{2}&0&\cdots&0&0&0&\cdots&0\\ 0&2\sqrt{2}&\cdots&0&0&0&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&0&\cdots&2\sqrt{2}&0&0&\cdots&0\\ 0&0&\cdots&0&B_{10}&0&\cdots&0\\ 0&0&\cdots&0&B_{20}&B_{10}&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&0&\cdots&0&B_{1[\frac{n-1}{2}]}&B_{1,[\frac{n-1}{2}]-1}&\cdots&B_{10}\\ \end{matrix}\right).$

上述矩阵的行列式为

$|A|=(-1)^{[\frac{n-1}{2}]+1}(2\sqrt{2})^{[\frac{n}{2}]+1}(\frac{\sqrt{6}}{4})^{[\frac{n-1}{2}]+1}\neq0.$

所以 $c_{1i}\ (i=0,1,2,\cdots,[\frac{n}{2}])$ 和 $c_{2i}\ (i=0,1,2,\cdots,[\frac{n-1}{2}])$ 是相互独立的.

类似于命题 3.1, 应用引理 3.3、引理 3.4 和引理 3.5 可以得到 $M(h)$ 在尖点环附件的渐近展式.

命题 3.2 当 $0<\frac{1}{3}-h\ll1$ 时, $M(h)$ 的渐近展开式为

$M(h)=\sum\limits_{i=0}^{[\frac{n-1}{2}]}d_{1i}|u|^{i+\frac{5}{6}}+\sum\limits_{i=0}^{[\frac{n-2}{2}]}d_{2i}|u|^{i+\frac{7}{6}}+ \sum\limits_{i=0}^{\infty}d_{3i}|u|^i\\ +\sqrt{|u|}\sum\limits_{i=1}^\infty d_{4,2i-1}|u|^i+ +\ln|u| \sum\limits_{i=0}^{\infty}d_{5i}|u|^i,$

其中 $u=h-\frac{1}{3}$, $d_{1i}$ $(i=0,1,2,\cdots,[\frac{n-1}{2}])$, $d_{2i}$ $(i=0,1,2,\cdots,[\frac{n-2}{2}])$, $d_{3i}$ $(i=0,1,2,\cdots,[\frac{n}{2}])$, $d_{4i}$ $(i=1,3,5,\cdots,2[\frac{n+1}{4}]-1)$ 和 $d_{5i}$ $(i=0,1,2,\cdots,[\frac{n-3}{2}])$ 是相互独立的, 并且

$d_{1i}=(-1)^i\rho_1b^+_i,\ d_{2i}=(-1)^i\rho_2c^+_i, \ d_{3i}=\bar{d}_{1i}+\bar{d}_{2,2i-2}, \ d_{4i}=\bar{d}_{2,2i-1},\ \bar{d}_{2i}=\zeta_{1i}+\zeta_{2i},\\ d_{5i}=\begin{cases} \tilde{d}_{1i}+\tilde{d}_{2i}+\sigma_2c^-_{i-1}, 0\leq i\leq[\frac{n-3}{2}]+2,\\ \tilde{d}_{1i}+\tilde{d}_{2i},\qquad \qquad i\geq[\frac{n-3}{2}]+3, \end{cases}\\ \tilde{d}_{1i}=\begin{cases} \sum\limits_{k=0}^{i-1}\varsigma_{1,i-k}b^-_k,\quad\ 1\leq i\leq[\frac{n-1}{2}]+1,\\ \sum\limits_{k=0}^{[\frac{n-1}{2}]+1}\varsigma_{1,i-k}b^-_k, i\geq[\frac{n-1}{2}]+2, \end{cases} \tilde{d}_{2i}=\begin{cases} \sum\limits_{k=0}^{i}\varsigma_{1,i-k}d^-_k,\ 0\leq i\leq[\frac{n-3}{2}],\\ \sum\limits_{k=0}^{[\frac{n-3}{2}]}\varsigma_{1,i-k}d^-_k, i\geq[\frac{n-3}{2}]+1, \end{cases}\\ \bar{d}_{1i}=\begin{cases} \sum\limits_{k=1}^5\tau_{ki}+\sigma_1 b^-_i+\sigma_3d^-_i,\ 0\leq i\leq[\frac{n-3}{2}],\\ \sum\limits_{k=1}^5\tau_{ki}+\sigma_1 b^-_i,\qquad i=[\frac{n-3}{2}]+1,\\ \sum\limits_{k=1}^5\tau_{ki},\qquad\qquad \qquad\ i\geq[\frac{n-3}{2}]+2, \end{cases}\\ \tau_{1i}=\begin{cases} \sum\limits_{k=0}^{i}\rho_{0,i-k}a^+_k,\ 0\leq i\leq[\frac{n}{2}],\\ \sum\limits_{k=0}^{[\frac{n}{2}]}\rho_{0,i-k}a^+_k,\ i\geq[\frac{n}{2}]+1, \end{cases} \tau_{2i}=\begin{cases} \sum\limits_{k=0}^{i}\rho_{1,i-k}b^+_k,\ 0\leq i\leq[\frac{n-1}{2}],\\ \sum\limits_{k=0}^{[\frac{n-1}{2}]}\rho_{1,i-k}b^+_k, i\geq[\frac{n-1}{2}]+1, \end{cases}\\ \tau_{3i}=\begin{cases} \sum\limits_{k=0}^{i}\rho_{2,i-k}c^+_k,\ 0\leq i\leq[\frac{n-2}{2}],\\ \sum\limits_{k=0}^{[\frac{n-2}{2}]}\rho_{2,i-k}c^+_k, i\geq[\frac{n-2}{2}]+1, \end{cases} \tau_{4i}=\begin{cases} \sum\limits_{k=0}^{i}\sigma_{0,i-k}a^-_k,\ 0\leq i\leq[\frac{n}{2}],\\ \sum\limits_{k=0}^{[\frac{n}{2}]}\sigma_{0,i-k}a^-_k,\ i\geq[\frac{n}{2}]+1, \end{cases}\\ \tau_{5i}=\begin{cases} \sum\limits_{k=0}^{i}\sigma_{2,i-k}c^-_k,\ 0\leq i\leq[\frac{n-2}{2}],\\ \sum\limits_{k=0}^{[\frac{n-2}{2}]}\sigma_{2,i-k}c^-_k, i\geq[\frac{n-2}{2}]+1, \end{cases}\zeta_{1i}=\begin{cases} \sum\limits_{k=0}^{[\frac{i}{2}]}\sigma_{1,i-2k}b^-_k,\ 0\leq i \leq2[\frac{n-1}{2}],\\ \sum\limits_{k=0}^{[\frac{n-1}{2}]}\sigma_{1,i-2k}b^-_k, i \geq2[\frac{n-1}{2}]+1, \end{cases}\\ \zeta_{2i}=\begin{cases} \sum\limits_{k=0}^{[\frac{i}{2}]}\sigma_{3,i-2k}d^-_k,\ \ 0\leq i \leq2[\frac{n-3}{2}],\\ \sum\limits_{k=0}^{[\frac{n-3}{2}]}\sigma_{3,i-2k}d^-_k,\ i \geq2[\frac{n-3}{2}]+1. \end{cases} $

证 把 (3.9) 和 (3.14) 式带入 (2.2) 式即可得 (3.16) 式. 类似于命题 3.1 可以证明 $d_{1i}$ $(i=0,1,2,$ $\cdots,[\frac{n-1}{2}])$, $d_{2i}\ (i=0,1,2,\cdots,[\frac{n-2}{2}])$, $d_{3i}\ (i=0,1,2,\cdots,[\frac{n}{2}])$, $d_{4i}\ (i=1,3,5,\cdots,2[\frac{n+1}{4}]-1)$ 和 $d_{5i}$ $(i=0,1,2,\cdots,[\frac{n-3}{2}])$ 是相互独立的.

定理 3.1 扰动微分系统 (1.1) 在原点附近至少有 $n$ 个极限环.

证 由命题 3.1 可知, $M(h)$ 中的系数 $c_{1i}$ $(i=0,1,2,\cdots,[\frac{n}{2}])$ 和 $c_{2i}$ $(i=0,1,2,\cdots,[\frac{n-1}{2}])$ 是相互独立的, 所以, 当 $n$ 是偶数时, 可以选取

$0<c_{10}\ll-c_{20}\ll c_{11}\ll-c_{21}\ll c_{12}\ll-c_{22}\ll\cdots\ll c_{1,[\frac{n}{2}]-1}\ll-c_{2,[\frac{n-1}{2}]}\ll c_{1,[\frac{n}{2}]}.$

当 $n$ 是奇数时, 可以选取

$0<c_{10}\ll-c_{20}\ll c_{11}\ll-c_{21}\ll c_{12}\ll-c_{22}\ll\cdots\ll c_{1,[\frac{n}{2}]}\ll-c_{2,[\frac{n-1}{2}]}.$

因此, 一阶 Melnikov 函数 $M(h)$ 在 $h=0$ 附近有 $[\frac{n}{2}]+[\frac{n-1}{2}]+1=n$ 个正的简单零点. 由文献 [9] 和 [16] 可知, 对任给的闭区间 $[a,b]\subset(0,\frac{1}{3})$, 当 $h\in [a,b]$, 且 $|\varepsilon|$ 充分小时, $F(h,\varepsilon)\in C^\infty$. 由隐函数定理, 系统 (1.1) 在原点附近存在$n$个极限环.

定理 3.2 扰动微分系统 (1.1) 在尖点环附近至少有 $2n+[\frac{n+1}{4}]-1$ 个极限环.

证 由命题 3.2 可知, $M(h)$ 中的系数 $d_{1i}\ (i=0,1,2,\cdots,[\frac{n-1}{2}])$, $d_{2i}$ $(i=0,1,2,\cdots,[\frac{n-2}{2}])$, $d_{3i}$ $(i=0,1,2,\cdots,[\frac{n}{2}])$, $d_{4i}$ $(i=1,3,5,\cdots,2[\frac{n+1}{4}]-1)$ 和 $d_{5i}$ $(i=0,1,2,\cdots,[\frac{n-3}{2}])$ 是相互独立的, 所以, 当 $n$ 是偶数时, 可以选取

$0<-d_{50}\ll d_{30}\ll-d_{10}\ll d_{51}\ll -d_{31}\ll d_{20}\ll-d_{41}\ll d_{11}\ll -d_{52}\\ \ll\cdots\ll (-1)^\frac{n}{2}d_{3,[\frac{n}{2}]}\ll (-1)^{\frac{n}{2}+1}d_{2,[\frac{n-2}{2}]},$

当 $n$ 是奇数时, 可以选取

$0<-d_{50}\ll d_{30}\ll-d_{10}\ll d_{51}\ll -d_{31}\ll d_{20}\ll-d_{41}\ll d_{11}\ll -d_{52}\\ \ll\cdots\ll (-1)^{[\frac{n}{2}]-1}d_{3,[\frac{n}{2}]}\ll (-1)^{[\frac{n}{2}]}d_{2,[\frac{n-2}{2}]}\ll (-1)^{[\frac{n}{2}]+1}d_{1,[\frac{n-1}{2}]},$

因此, 一阶 Melnikov 函数 $M(h)$ 在 $h=\frac{1}{3}$ 附近有 $2n+[\frac{n+1}{4}]-1$ 个正的简单零点. 所以系统 (1.1) 在尖点环附近存在 $2n+[\frac{n+1}{4}]-1$ 个极限环.

参考文献

Tse C, Bernardo M.

Complex behavior in switching power converter

Proceeding of IEEE, 2002, 90(5): 768-781

DOI:10.1109/JPROC.2002.1015006      URL     [本文引用: 1]

Kember S, Babitsky V.

Excitation of vibro-impact systems by periodic impulses

J Sound Vib, 1999, 227(2): 427-447

DOI:10.1006/jsvi.1999.2353      URL     [本文引用: 1]

黄立宏, 郭振远, 王佳伏. 右端不连续微分方程理论与应用. 北京: 科学出版社, 2011

[本文引用: 1]

Huang L H, Guo Z Y, Wang F J. Theory and Application of Differential Equations with Discontinuous Right-Hand Sides. Beijing: Science Press, 2011

[本文引用: 1]

Zou Y, Kupper T, Beyn W.

Generalized Hopf bifurcation for planar Filippov systems continuous at the origin

J Nonlinear Sci, 2006, 16(2): 159-177

DOI:10.1007/s00332-005-0606-8      URL     [本文引用: 1]

Simpson D, Meiss J.

Andronov-Hopf bifurcation in planar, piecewise-smooth, continuous flows

Phys Lett A, 2007, 371(3): 213-220

DOI:10.1016/j.physleta.2007.06.046      URL     [本文引用: 1]

Virgin L, Begley C.

Grazing bifurcations and basins of attraction in an impact-friction oscillator

Physica D, 1999, 130: 43-57

DOI:10.1016/S0167-2789(99)00016-0      URL     [本文引用: 1]

Kukučka P.

Melnikov method for discontinuous planar systems

Nonlinear Anal, 2007, 66: 2698-2719

DOI:10.1016/j.na.2006.04.001      URL     [本文引用: 1]

Li L, Huang L.

Concurrent homoclinic bifurcation and Hopf bifurcation for a class of planar Filippov systems

J Math Anal Appl, 2014, 411: 83-94

DOI:10.1016/j.jmaa.2013.09.025      URL     [本文引用: 1]

Liu X, Han M A.

Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems

Int J Bifurc Chaos, 2010, 20(5): 1379-1390

DOI:10.1142/S021812741002654X      URL     [本文引用: 4]

In this paper, the general perturbation of piecewise Hamiltonian systems on the plane is considered. When the unperturbed system has a family of periodic orbits, similar to the perturbations of smooth system, an expression of the first order Melnikov function is derived, which can be used to study the number of limit cycles bifurcated from the periodic orbits. As applications, the number of bifurcated limit cycles of several concrete piecewise systems are presented.

Llibre J, Lopes B, Moraes J.

Limit cycles for a class of continuous and discontinuous cubic polynomial differential systems

Qual Theory Dyn Syst, 2014, 13: 129-148

DOI:10.1007/s12346-014-0109-9      URL     [本文引用: 1]

Li F, Yu P, Tian Y, Liu Y.

Center and isochronous center conditions for switching systems associated with elementary singular points

Commun Nonlinear Sci Numer Simul, 2015, 28: 81-97

DOI:10.1016/j.cnsns.2015.04.005      URL     [本文引用: 1]

Guo L, Yu P, Chen Y.

Bifurcation analysis on a class of $Z_2$-equivariant cubic switching systems showing eighteen limit cycles

J Differential Equations, 2019, 266: 1221-1244

DOI:10.1016/j.jde.2018.07.071      URL     [本文引用: 1]

Liang F, Han M.

Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems

Chaos Solitons Fractals, 2012, 45: 454-464

DOI:10.1016/j.chaos.2011.09.013      URL     [本文引用: 1]

Liang F, Han M, Zhang X.

Bifurcation of limit cycles from generalized homoclinic loops in planar piecewise smooth systems

J Differential Equations, 2013, 255: 4403-4436

DOI:10.1016/j.jde.2013.08.013      URL     [本文引用: 1]

Xiong Y, Han M.

Limit cycles appearing from a generalized heteroclinic loop with a cusp and a nilpotent saddle

J Differential Equations, 2021, 303: 575-607

DOI:10.1016/j.jde.2021.09.031      URL     [本文引用: 1]

Han M, Sheng L.

Bifurcation of limit cycles in piecewise smooth systems via Melnikov function

J Appl Anal Comput, 2015, 5: 809-815

[本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发