计算自旋轨道耦合 Spin-2 BEC 基态的带拉格朗日乘子的正规梯度流法

计算自旋轨道耦合 Spin-2 BEC 基态的带拉格朗日乘子的正规梯度流法

袁永军^,

计算与随机数学教育部重点实验室 & 湖南师范大学数学与统计学院长沙 410081

A Normalized Gradient Flow with Lagrange Multipliers for Computing Ground States of Spin-Orbit Coupled Spin-2 Bose-Einstein Condensates

Yuan Yongjun^,

LCSM (MOE) & School of Mathematics and Statistics, Hunan Normal University, Changsha 410081

收稿日期: 2022-08-26 修回日期: 2023-03-23

基金资助:

国家自然科学基金(11971007)

Received: 2022-08-26 Revised: 2023-03-23

Fund supported:

NSFC(11971007)

作者简介 About authors

袁永军，Email:yyj1983@hunnu.edu.cn

摘要

该文设计带拉格朗日乘子的正规梯度流法 (GFLM) 模拟自旋轨道耦合 Spin-2 玻色-爱因斯坦凝聚 (BEC) 的基态. 发掘投影系数间的隐含关系, 解决了模型中已有条件 (总质量及总磁场量守恒) 不足以确定所有投影系数的困难. 对循环型/铁磁体系下具有不同势函数的自旋轨道耦合 Spin-2 BEC 的基态进行了大量数值试验, 验证了算法的有效性, 并揭示了自旋轨道耦合 Spin-2 BEC 的条纹状基态与晶格状基态随自旋轨道耦合系数相互转化的相变规律.

关键词： 玻色-爱因斯坦凝聚; 基态; 正规梯度流法; 拉格朗日乘子

Abstract

In this paper, a normalized gradient flow with Lagrange multipliers is designed to compute ground states of spin-orbit coupled Spin-2 Bose-Einstein condensates. By excavating the implicit relation between projection coefficients, the difficult that the existed conditions (the conservation of total mass and magnetization) of the model problem is insufficient to determine all the projection coefficients, is overcome. Extensive numerical experiments are done to compute the ground states of spin-orbit coupled Spin-2 BECs with cyclic/ferromagenetic interactions. As a result, the effectiveness of the two algorithms is verified, and the phase transformation law about how the stripe pattern ground states and the square-lattice pattern ground states of spin-orbit coupled Spin-2 BECs change to each other with the spin-orbit coupling parameter,are revealed.

Keywords： Bose-Einstein condensate; Ground state; Normalized gradient flow; Lagrange multiplier

PDF (2438KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

袁永军. 计算自旋轨道耦合 Spin-2 BEC 基态的带拉格朗日乘子的正规梯度流法[J]. 数学物理学报, 2023, 43(5): 1607-1619

Yuan Yongjun. A Normalized Gradient Flow with Lagrange Multipliers for Computing Ground States of Spin-Orbit Coupled Spin-2 Bose-Einstein Condensates[J]. Acta Mathematica Scientia, 2023, 43(5): 1607-1619

1 引言

玻色-爱因斯坦凝聚 (BEC) 被称为世界物质第五态, 是指玻色子在温度接近绝对零度时达到的物质状态. 它由玻色和爱因斯坦在 1924-1925 年预测^[9,13,14], 并于 1995 年首次在物理实验中实现^[1,10,12].

在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋 $^{23}\mathrm{Na}$ 气体中产生了旋量 BEC, 其内部自旋自由度被激活^[21]. 在光阱中, 不同超精细态的粒子在空间中具有不同的角动量, 从而产生丰富的自旋结构. 自旋量子数为 $\mathcal{F}$ ( $\mathcal{F}$ 为正整数) 的 BEC, 被称为 Spin- $\mathcal{F}$ BEC, 存在 2 $\mathcal{F}$ +1 个超精细态, 且旋量凝聚态可用 2 $\mathcal{F}$ +1 个分量的矢量波函数进行刻画^[15,16,22]. 特别地, 由于粒子自旋和粒子运动的相互影响会产生自旋轨道耦合 (SOC) 效应, 近年, Lin 等^[18,19,20] 在中性原子的 BEC 实验中, 成功诱导了自旋轨道耦合旋量 BEC.

在平均场意义下, 温度 $T\ll$ 临界温度 $T_c$ 时, Spin- $\mathcal{F}$ BEC 可用 2 $\mathcal{F}+1$ 个耦合的 Gross-Pitaevskii 方程 (CGPEs) 来刻画. 本文研究自旋轨道耦合 Spin-2 BEC 模型, 其波函数 $\Psi(\mathbf{x},t)= {(\psi_{-2}(\mathbf{x},t),\psi_{-1}(\mathbf{x},t), \psi_0(\mathbf{x},t),\psi_{1}(\mathbf{x},t),\psi_{2}(\mathbf{x},t))}^{T}$ 满足无量纲化的 CGPEs

$\begin{equation} \begin{split} {\rm i}\partial_{t}\psi_{\pm2} =&[H+\beta_{0}\rho(\Psi)\pm 2\beta_{1}F_{z}(\Psi)]\psi_{\pm2}+\beta_{1}F_{\mp}(\Psi)\psi_{\pm1} +\frac{\beta_{2}}{\sqrt{5}}A_{00}(\Psi)\bar{\psi}_{\mp2}\\&-\gamma({\rm i}\partial_{y}\psi_{\pm1}\mp \partial_{x}\psi_{\pm1}), \end{split} \end{equation}$

(1.1)

$\begin{equation} \begin{split} {\rm i}\partial_{t}\psi_{\pm1} =&[H+\beta_{0}\rho(\Psi)\pm\beta_{1}F_{z}(\Psi)]\psi_{\pm1}+\beta_{1}(\frac{\sqrt{6}}{2}F_{\mp}(\Psi)\psi_{0}+F_{\pm}(\Psi)\psi_{\pm2})\\& -\frac{\beta_{2}}{\sqrt{5}} A_{00}(\Psi)\bar{\psi}_{\mp1} -\gamma[{\rm i}\partial_{y}(\psi_{\pm2}+\frac{\sqrt{6}}{2}\psi_{0})\mp \partial_{x}(\frac{\sqrt{6}}{2}\psi_{0}-\psi_{\pm2})], \end{split} \end{equation}$

(1.2)

$\begin{equation} \begin{split} {\rm i}\partial_{t}\psi_{0} =&[H+\beta_{0}\rho(\Psi)]\psi_{0}+\frac{\sqrt{6}}{2}\beta_{1}[F_{+}(\Psi)\psi_{1}+F_{-}(\Psi)\psi_{-1}] +\frac{\beta_{2}}{\sqrt{5}}A_{00}(\Psi)\bar{\psi}_{0}\\ & -\frac{\sqrt{6}}{2}\gamma[{\rm i}\partial_{y}(\psi_{1}+\psi_{-1})- \partial_{x}(\psi_{-1}-\psi_{1})], \end{split} \end{equation}$

(1.3)

初始条件

$\begin{equation} \psi_{\ell}(\mathbf{x},0) = \psi_{\ell}^{0}(\mathbf{x}),\quad \mathbf{x}\in \mathbb{R}^{d},\quad\ell = -2,-1,0,1,2. \end{equation}$

(1.4)

其中

$H=-\frac{1}{2}\nabla^{2}+V(\mathbf{x}), \rho(\Psi)=\sum_{\ell=-2}^{2}|\psi_{\ell}(\mathbf{x},t)|^{2},$

$F_{z}(\Psi)=2(|\psi_{2}|^2-|\psi_{-2}|^2)+|\psi_{1}|^2-|\psi_{-1}|^2,$

$F_{+}(\Psi)=\bar{F_{-}}({\Psi})=2(\bar{\psi}_{2}\psi_{1}+\bar{\psi}_{-1}\psi_{-2})+\sqrt{6}(\bar{\psi}_{1}\psi_{0}+\bar{\psi}_{0}\psi_{-1}),$

$A_{00}(\Psi(\mathbf{x},t))=\frac{1}{\sqrt{5}}[t)],$

这里 $t$ 是时间, i 是虚数单位, $\mathbf{x}\in \mathbb{R} ^{d} (d=2,3)$ 是笛卡尔坐标向量, $\gamma$ 是自旋轨道耦合强度, $\rho$ 是总密度, $\beta_{2}, \beta_{1}, \beta_{0}$ 依次是自旋单线态, 自旋交换和自旋独立相互作用实常数, $V(\mathbf{x})$ 是实值外势函数, 其常见的取法有调和势函数和光学晶格势函数. $V(\mathrm{x})$ 取调和势函数时,

$\begin{equation*} V_{har}(\mathbf{x})=\frac{1}{2}\begin{cases} \omega_{x}^{2}x^{2} + \omega_{y}^{2}y^{2}, &{d=2},\\ \omega_{x}^{2}x^{2} + \omega_{y}^{2}y^{2} + \omega_{z}^{2}z^{2}, &{d=3}, \end{cases} \end{equation*}$

其中 $\omega_{\nu}$ 表示 $\nu$ -方向上 ( $\nu=x,y,z$ ) 的势阱频率. $V(\mathbf{x})$ 取光学晶格势函数时,

$V_{opt}(\mathrm{\nu})=I_{\nu}E_{\nu}\sin^2(\hat{q_{\nu}}\nu), \nu=x,y,z,$

这里 $E_{\nu}=\frac{1}{2}\hbar^{2}\hat{q_{\nu}}^{2}$ 表示反冲常量, $I_{\nu}$ 是提供激光强度的无量纲化参数.

波函数 $\Psi(\mathbf{x},t)$ 满足以下三个不变性

质量守恒

$\begin{equation}\mathcal{N}(t):=\mathcal{N}(\Psi(\cdot,t)):=\sum_{\ell=-2}^{2}\int_{\mathbb{R}^d}|\psi_{\ell}(\mathbf{x},t)|^{2}{\rm d}\mathbf{x} \equiv1,\quad t\geq 0; \end{equation}$

(1.5)

磁场量守恒

$\begin{equation} \mathcal{M}(t):=\mathcal{M}(\Psi(\cdot,t)):=\sum_{\ell=-2}^{2}\int_{\mathbb{R}^d}\ell|\psi_\ell(\mathbf{x},t)|^2{\rm d}\mathbf{x}\equiv M,\quad M\in[-2,2]; \end{equation}$

(1.6)

单个粒子能量守恒

$\begin{equation} \begin{split} E(t):=\ &E(\Psi(\cdot, t))\\:=\ &\int_{\mathbb{R}^d}\bigg\{\sum\limits_{\ell=-2}^2\left(\frac{1}{2}|\nabla\psi_\ell|^2+V(\mathbf{x})|\psi_\ell|^2 )+\frac{\beta_0}{2}\rho^2+\frac{\beta_1}{2} \left(|F_+(\Psi)|^2+|F_z(\Psi)|^2 \right)\right)\\ &+\frac{\beta_2}{2}|A_{00}(\Psi)|^2-\gamma \left[{\rm i}(\partial_{y}\Psi)^{T} f_{x}{\bar{\Psi}}-(\partial_{x}\Psi)^{T} f_{y}{\bar{\Psi}} \right]\bigg\}{\rm d}\mathbf{x} \\ \equiv\ & E(\Psi(\cdot,0))=:E_0,\quad t\geq0, \end{split} \end{equation}$

(1.7)

其中 $\mathcal{N}$ 表示总质量, $\mathcal{M}$ 表示总磁场量, $\bar{\Psi}$ 和 ${\Psi}^{T}$ 分别表示 $\Psi$ 的共轭和转置. 显然能量 $E(\Psi)$ 可表示为动能 $E_{\rm kin}(\Psi)$ , 势能 $E_{\rm pot}(\Psi)$ , 相互作用能 $E_{\rm spin}(\Psi)$ 和自旋轨道耦合能 $E_{\rm soc}(\Psi)$ 之和, 即

$\begin{equation*} E(\Psi)=E_{\rm kin}(\Psi)+E_{\rm pot}(\Psi)+E_{\rm spin}(\Psi)+E_{\rm soc}(\Psi), \end{equation*}$

其中

$\begin{equation*} \begin{aligned} E_{\rm kin}(\Psi)=\frac{1}{2}\int_{\mathbb{R}^d} \left(\sum\limits_{\ell=-2}^2 |\nabla\psi_\ell|^2 \right){\rm d}\mathbf{x}, \end{aligned} \end{equation*}$

$\begin{equation*} E_{\rm pot}(\Psi)=\int_{\mathbb{R}^d} \left[\sum\limits_{\ell=-2}^2 V(\mathbf{x})|\psi_\ell|^2 \right]{\rm d}\mathbf{x}, \end{equation*}$

$\begin{equation*} E_{\rm soc}(\Psi)=-\gamma \int_{\mathbb{R}^d} \left[{\rm i}(\partial_{y}\Psi)^{T} f_{x}{\bar{\Psi}}-(\partial_{x}\Psi)^{T} f_{y}{\bar{\Psi}} \right]{\rm d}\mathbf{x}, \end{equation*}$

$\begin{equation*} \begin{split} E_{\rm spin}(\Psi)=\int_{\mathbb{R}^d} \left[\frac{\beta_0}{2}\rho(\Psi)^2 +\frac{\beta_1}{2} \left(|F_+(\Psi)|^2+|F_z(\Psi)|^2 \right)+\frac{\beta_2}{2}|A_{00}(\Psi)|^2\right] {\rm d}\mathbf{x}, \end{split} \end{equation*}$

$f_{x}$ 和 $f_{y}$ 是 5

$\begin{equation*} {\begin{matrix} f_{x}=\begin{bmatrix} 0&1&0&0&0\\ 1&0& \frac{\sqrt{6}}{2}&0&0\\ 0& \frac{\sqrt{6}}{2}&0& \frac{\sqrt{6}}{2}&0 \\ 0&0& \frac{\sqrt{6}}{2} &0&1\\ 0&0&0&1&0 \\ \end{bmatrix}, \quad f_{y}=\begin{bmatrix} 0&-1&0&0&0\\ 1&0& -\frac{\sqrt{6}}{2}&0&0\\ 0& \frac{\sqrt{6}}{2}&0& -\frac{\sqrt{6}}{2}&0 \\ 0&0& \frac{\sqrt{6}}{2} &0&-1\\ 0&0&0&1&0 \\ \end{bmatrix}. \end{matrix}} \end{equation*}$

基态模拟是 BEC 研究的重要问题. 自旋轨道耦合 Spin-2 BEC 的基态 $\Phi_{g}(\mathbf{x})$ 定义为

$\begin{equation} E\left(\Phi_{g}\right) = \min_{\Phi\in S}E(\Phi), \end{equation}$

(1.8)

其中非凸集 $S$ 为

$\begin{equation} S=\{\Phi = (\phi_{-2},\phi_{-1},\phi_{0},\phi_{1},\phi_{2})^{T}| N(\Phi) = 1, \mathcal{M}(\Phi) = M, E(\Phi)<\infty\}. \end{equation}$

(1.9)

近年已有大量的数值方法模拟 BEC 的基态. Bao 等早期采用直接最小化能量泛函法来求解基态^[6]. 随后, Bao 和 Du 提出了一种简单且广泛适用的方法, 即正规梯度流法^[4]来计算 BEC 的基态. 对于旋转单组份 BEC 模型, Bao 等采用向后欧拉有限差分离散的连续梯度流法^[8]研究了模型的基态, 对称态和中心涡态以及能量和化学势图. Antoine 和 Tang 等提出了效率更高的预条件共轭梯度法 (PCG)^[2].

对于旋量 BEC 的基态模拟, Bao 和 Wang 为 Spin-1 BEC 构造了连续梯度流并对其采用 Crank-Nicolson 有限差分进行离散^[7]. 随后, Bao 等利用离散正规梯度流法计算 Spin-1 和 Spin-2 BEC 的基态^[3,5], 其核心在于发掘投影系数间的隐含关系, 连同模型中的总质量和总磁场量守恒关系, 使得投影步骤所需的所有投影系数可被唯一确定. 此外, Cai 和 Liu 提出了模拟不带自旋轨道耦合项的 Spin- $\mathcal{F}$ BEC 基态的带拉格朗日乘子的梯度流法^[11,17].

对于自旋轨道耦合旋量 BEC 模型, Yuan 等^[23] 提出了投影梯度流法计算自旋轨道耦合 Spin-1 BEC 的基态. 该方法采用空间二阶有限差分和时间 Grank-Nicolson 方法离散连续梯度流, 具有总质量、总磁场量守恒及能量递减的性质. 然而, 自旋轨道耦合 Spin-2 BEC 模型具有复杂的自旋交换项和自旋单线态项, 其基态解在自旋轨道耦合效应下具有复杂的基态相, 可呈现细密的条纹状和晶格状两种图案. 这些特点对模拟自旋轨道耦合 Spin-2 BEC 基态的数值算法在精度与效率方面提出了新的挑战. 目前, 关于自旋轨道耦合 Spin-2 BEC 基态模拟的数值结果十分有限. 本文将带拉格朗日乘子的梯度流算法^[11,17] 推广到自旋轨道耦合 Spin-2 BEC 的基态模拟. 该方法在每步迭代只需求解一个常系数椭圆方程(组), 易实施且效率高.

本文结构安排如下: 第 2 节介绍带拉格朗日乘子的正规梯度法, 给出该方法的梯度流方程及其投影系数的确定方法; 第 3 节介绍其离散格式; 第 4 节给出数值结果.

2 带拉格朗日乘子的正规梯度流法

自旋轨道耦合 Spin-2 BEC (1.1)-(1.3) 对应的连续正规梯度流 (CNGF) 定义为

$\begin{equation} \begin{split} \partial_{t}\phi_{\pm2} &=-(H+\beta_{0}\rho\pm 2\beta_{1}F_{z})\phi_{\pm2}-\beta_{1}F_{\mp}\phi_{\pm1} -\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{\mp2}\\ &\quad+\gamma({\rm i}\partial_{y}\phi_{\pm1}\mp\partial_{x}\phi_{\pm1})+(\mu\pm2\lambda)\phi_{\pm2}\\ &\triangleq -\left[g_{\pm2}(\Phi)-(\mu\pm2\lambda)\phi_{\pm2}\right],\quad t\geq 0, \end{split} \end{equation}$

(2.1)

$\begin{equation} \begin{split} \partial_{t}\phi_{\pm1} =&-(H+\beta_{0}\rho\pm\beta_{1}F_{z})\phi_{\pm1}-\beta_{1}\left(\frac{\sqrt{6}}{2}F_{\mp}\phi_{0}+F_{\pm}\phi_{\pm2}\right) +\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{\mp1} \\ &\quad+\gamma\left[{\rm i}\partial_{y}(\phi_{\pm2}+\frac{\sqrt{6}}{2}\phi_{0})\mp \partial_{x}\left(\frac{\sqrt{6}}{2}\phi_{0}-\phi_{\pm2}\right)\right]+(\mu\pm\lambda)\phi_{\pm1},\\ &\hspace{-0.4cm}\triangleq -\left[g_{\pm1}(\Phi)-(\mu\pm\lambda)\phi_{\pm1}\right], \end{split} \end{equation}$

(2.2)

$\begin{equation} \begin{split} \partial_{t}\phi_{0} =&-(H+\beta_{0}\rho)\phi_{0}-\frac{\sqrt{6}}{2}\beta_{1}(F_{+}\phi_{1}+F_{-}\phi_{-1}) -\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{0}\\ & +\frac{\sqrt{6}}{2}\gamma\left[{\rm i}\partial_{y}(\phi_{1}+\phi_{-1})-\partial_{x}(\phi_{-1}-\phi_{1})\right]+\mu\phi_{0}\\ &\hspace{-0.4cm}\triangleq -\left[g_{0}(\Phi)-\mu\phi_{0}\right]. \end{split} \end{equation}$

(2.3)

这里 $\mu(\Phi)$ 与 $\lambda (\Phi)$ 为拉格朗日乘子, 其选取使 $\Phi$ 满足总质量和总磁场量守恒. 事实上, 由

$\frac{\rm d}{{\rm d}t}\sum_{\ell=-2}^{2}\|\phi_{\ell}(\cdot,t)\|^2 = 0,\qquad \frac{\rm d}{{\rm d}t}\sum_{\ell=-2}^{2}\ell \|\phi_{\ell}(\cdot,t)\|^2 = 0,$

联立 (2.1)-(2.3) 式并以 $\left(\mu(\Phi)+\ell\lambda(\Phi)\right)\phi_\ell \ (\ell=0,\pm1,\pm 2)$ 代替其中的拉格朗日乘子项, 解得

$\begin{equation} \begin{cases}\mu(\Phi)=\frac{P(\Phi)Q(\Phi)-MR(\Phi)}{P(\Phi)-M^{2}},\\\lambda(\Phi)=\frac{R(\Phi)-MQ(\Phi)}{P(\Phi)-M^{2}}, \end{cases} \end{equation}$

(2.4)

其中

$P(\Phi)=4\left(\|\phi_{2}\|^{2}+\|\phi_{-2}\|^{2})+(\|\phi_{1}\|^{2}+\|\phi_{-1}\|^{2}\right),$

$Q(\Phi)=\sum_{\ell=-2}^2\big\langle g_\ell(\Phi),\phi_\ell\big\rangle,\quad R(\Phi)=\sum_{\ell=-2}^2\big\langle g_\ell(\Phi),\ell\phi_\ell\big\rangle.$

这里及下文, 如无特殊说明, 范数 $\|\cdot\|$ 均表示 $L^2$ 范数 $\|\cdot\|_{L^2}$ .

易知连续正规梯度流 (2.1)-(2.3) 式具有总质量守恒、总磁场量守恒和能量稳定性, 但由于其为非线性积分方程组, 直接离散求解往往计算量大. 为避免这一困难, 下面考虑其一阶分裂格式导出的 GFLM. 取时间步长 $\Delta t$ , 并令时间序列 $t_{n} = n\Delta t (n = 0,1,2,\cdots )$ , 当 $t_{n-1}\leq t \leq t_{n}$ 时, GFLM 方法的梯度流

$\begin{equation} \begin{split} \partial_{t}\phi_{\pm2} &=-(H+\beta_{0}\rho\pm 2\beta_{1}F_{z})\phi_{\pm2}-\beta_{1}F_{\mp}\phi_{\pm1} -\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{\mp2}\\ &\quad+\gamma({\rm i}\partial_{y}\phi_{\pm1}\mp\partial_{x}\phi_{\pm1})+(\mu^{n-1}\pm2\lambda^{n-1})\phi_{\pm2} \\ &\triangleq -\left[g_{\pm2}(\Phi)-(\mu^{n-1}\pm2\lambda^{n-1})\phi_{\pm2}\right], \end{split} \end{equation}$

(2.5)

$\begin{equation} \begin{split} \partial_{t}\phi_{\pm1} =&-(H+\beta_{0}\rho\pm\beta_{1}F_{z})\phi_{\pm1}-\beta_{1}\left(\frac{\sqrt{6}}{2}F_{\mp}\phi_{0}+F_{\pm}\phi_{\pm2}\right) +\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{\mp1} \\ &\quad+\gamma\left[{\rm i}\partial_{y}(\phi_{\pm2}+\frac{\sqrt{6}}{2}\phi_{0})\mp \partial_{x}\left(\frac{\sqrt{6}}{2}\phi_{0}-\phi_{\pm2}\right)\right]+(\mu^{n-1}\pm\lambda^{n-1})\phi_{\pm1},\\ &\hspace{-0.4cm}\triangleq -\left[g_{\pm1}(\Phi)-(\mu^{n-1}\pm\lambda^{n-1})\phi_{\pm1}\right], \end{split} \end{equation}$

(2.6)

$\begin{equation} \begin{split} \partial_{t}\phi_{0} =&-(H+\beta_{0}\rho)\phi_{0}-\frac{\sqrt{6}}{2}\beta_{1}(F_{+}\phi_{1}+F_{-}\phi_{-1}) -\frac{\beta_{2}}{\sqrt{5}}A_{00}\bar{\phi}_{0}\\ & +\frac{\sqrt{6}}{2}\gamma\left[{\rm i}\partial_{y}(\phi_{1}+\phi_{-1})-\partial_{x}(\phi_{-1}-\phi_{1})\right]+\mu^{n-1}\phi_{0}\\ &\hspace{-0.4cm}\triangleq -\left[g_{0}(\Phi)-\mu^{n-1}\phi_{0}\right]. \end{split} \end{equation}$

(2.7)

投影步骤为

$\begin{equation} \phi_{\ell}(\mathbf{x},t_{n}):= \phi_{\ell}(\mathbf{x},t_{n}^{+}) = \alpha_{\ell}^{n}\phi_{\ell}(\mathbf{x},t_{n}^{-}),\quad \ell = -2,-1, \cdots,2, \end{equation}$

(2.8)

这里 $\phi_{\ell}(\mathbf{x},t_{n}^{\pm}) = \lim \limits_{t\rightarrow t_{n}^{\pm}}\phi_{\ell}(\mathbf{x},t)$ , $\mu^{n-1}=\mu(\Phi^{n-1})$ 及 $\lambda^{n-1}=\lambda(\Phi^{n-1})$ . 值得指出的是, 投影步骤等价于求解连续正规梯度流 (2.1)-(2.3) 式一阶分裂得到的第二个常微分方程组

$\begin{equation} \partial_{t}\phi_{\ell}(\mathbf{x},t)=\left[(\mu_{\Phi}(t)-\mu^{n-1})+\ell(\lambda_{\Phi}(t)-\lambda^{n-1})\right]\phi_{\ell}(\mathbf{x}, t),\quad \ell = -2,-1,\cdots,2, \end{equation}$

(2.9)

其中 $\mu_{\Phi}(t):=\mu\left(\Phi(\cdot,t) \right)$ 及 $\lambda_{\Phi}(t):=\lambda\left(\Phi(\cdot,t) \right)$ , 其解为

$\begin{eqnarray*} \phi_{\ell}(\mathbf{x}, t)&=&{\rm e}^{\int_{t_{n-1}}^{t}\left[(\mu_{\Phi}(s)-\mu^{n-1})+\ell(\lambda_{\Phi}(s)-\lambda^{n-1})\right]{\rm d}s}\phi_{\ell}(\mathbf{x}, t_{n-1}) :=\alpha_{\ell}^{n}\phi_{\ell}(\mathbf{x},t_{n-1}), \end{eqnarray*}$

这里 $\alpha_{\ell}^{n} (\ell = -2,-1,0,1,2)$ 即为第 $n$ 步的投影系数. 由 $\phi_{\ell}(\mathbf{x},t_n) (\ell = -2,-1,0,1, 2)$ 满足总质量守恒和总磁场量守恒, 有

$\begin{equation} \sum_{\ell=-2}^{2}(\alpha_{\ell}^{n})^{2}\|\phi_{\ell}(\cdot,t_{n}^{-})\|^2 = 1, \qquad \sum_{\ell=-2}^{2}\ell(\alpha_{\ell}^{n})^{2}\|\phi_{\ell}(\cdot,t_{n}^{-})\|^2 = M. \end{equation}$

(2.10)

因此, 为唯一确定所有投影系数 $\alpha_{\ell}^{n} (\ell = -2,-1,0,1,2)$ , 还需得到另外三个关于投影系数的方程. 受文献^[11]中对 $(\alpha_{\ell}^{n})^2$ 作泰勒展开思想的启发, 可得

$\begin{matrix} (\alpha_{\ell}^{n})^2&=&{\rm e}^{2\int_{t_{n-1}}^{t}\left[(\mu_{\Phi}(s)-\mu^{n-1})+\ell(\lambda_{\Phi}(s)-\lambda^{n-1})\right]{\rm d}s} \nonumber\\ &\approx&1+2\left[\int_{t_{n-1}}^{t}(\mu_{\Phi}(s)-\mu^{n-1}){\rm d}s+\ell\int_{t_{n-1}}^{t}(\lambda_{\Phi}(s)-\lambda^{n-1}){\rm d}s\right] \nonumber\\ &:=&c_{0} + \ell c_1. \end{matrix}$

(2.11)

将 (2.11) 式代入 (2.10) 式, 易得关于 $c_0,c_1$ 的一元一次方程组

$\begin{equation} m_0c_0+m_1c_1 = 1, \end{equation}$

(2.12)

$\begin{equation} m_1c_0+m_2c_1 = M, \end{equation}$

(2.13)

其中

$m_0=\sum_{\ell=-2}^{2}\|\phi_{\ell}(\cdot,t_{n}^{-})\|^2,\quad m_1=\sum_{\ell=-2}^{2}\ell \|\phi_{\ell}(\cdot, t_{n}^{-})\|^2, \quad m_2=\sum_{\ell=-2}^{2}\ell^2 \|\phi_{\ell}(\cdot,t_{n}^{-})\|^2.$

直接计算可得

$m_0m_2-m_1^2=\sum_{2\geq i>j\geq -2} (i-j)^2\|\phi_{i}(\cdot,t_{n}^{-})\|^2\|\phi_{j}(\cdot,t_{n}^{-})\|^2\geq 0.$

若假设至少有两个分量函数 $\phi_{\ell}(\cdot,t_{n}^{-}) (\ell = -2,-1,0,1,2)$ 中不为零函数, 则不等号严格成立, 此时方程 (2.12)-(2.13) 存在唯一解

$\begin{equation} c_0=\frac{m_2-m_1M}{m_0m_2-m_1^2},\qquad c_1=\frac{m_0M-m_1}{m_0m_2-m_1^2}. \end{equation}$

(2.14)

进而由 (2.11) 式得

$\begin{equation} \alpha_\ell^n={\rm e}^{\frac{c_0+\ell c_1-1}{2}}=\exp\left[\frac{m_2-m_1M+\ell(m_0M-m_1)}{m_0m_2-m_1^2}-\frac{1}{2} \right], \quad \ell=-2,-1,\cdots,2. \end{equation}$

(2.15)

3 离散格式

在势函数 $V(\mathbf{x})$ 作用下, 当 $|\mathbf{x} |\rightarrow+\infty$ 时, 模型的解指数衰减至零, 故计算基态时可将全空间截断成合适大小的有界区域, 并给定齐次 Dirichlet 边界条件或周期边界条件. 该文考虑二维矩形区域且带周期边界条件情形下的离散格式, 三维情形类似可得.

将有界区域 $(a,b)\times (c,d)$ 进行网格剖分, 令 $h_{x} = (b-a)/J > 0$ 且 $h_{y} = (d-c)/K >0$ , 这里的 $J,K$ 均为正偶数. 记网格点为

$x_{j} := a + jh_{x},\quad j=0,1,\cdots,J,\qquad y_{k} := b + kh_{y},\quad k=0,1,\cdots,K.$

设 $\Phi_{j,k}^{n} =(\phi_{j,k}^{n,-2},\phi_{j,k}^{n,-1},\phi_{j,k}^{n,0},\phi_{j,k}^{n,1},\phi_{j,k}^{n, 2})$ 为 $\Phi(x_{j},y_{k},t_{n})$ 的近似, $\Phi^{n}$ 是 $t=t_{n}$ 时的解向量, 其分量为 $\Phi_{j,k}^{n}$ . 引入常系数稳定项因子 $\varepsilon^n$ , 带拉格朗日乘子的梯度流 (2.5)-(2.8) 的离散格式为

$\begin{equation} \begin{split} \frac{\phi^{*,\ell}_{j,k} - \phi^{n-1,\ell}_{j,k}}{\Delta t}&=\frac{1}{2}\nabla_{h}^{2}\phi^{*,\ell}_{j, k}-\varepsilon^{n-1}\phi^{*,\ell}_{j,k} +\varepsilon^{n-1} \phi^{n-1,\ell}_{j,k} + G^{n-1,\ell}_{j,k}, \end{split} \end{equation}$

(3.1)

$\begin{equation} \phi_{j,k}^{n,\ell} = \alpha_{\ell}^{n} \phi_{j,k}^{*,\ell},\quad \ell =-2,\cdots,2. \\ \phi^{0,\ell}_{j,k}=\phi_{\ell}(x_{j},y_{k},t=0),\end{equation}$

(3.2)

其中

$\begin{align*} G^{n-1, -2}=\,&\left[\mu^{n-1}-2\lambda^{n-1}-V(\mathbf{x})-\beta_{0}\rho^{n-1}+2\beta_{1}F_{z}^{n-1}\right]\phi_{-2}^{n-1}-\beta_{1}F_{+}^{n-1}\phi_{-1}^{n-1}\\ & -\frac{\beta_{2}}{\sqrt{5}}A_{00}^{n-1}\bar{\phi_{2}}^{n-1}+\gamma({\rm i}\partial_{y} \phi_{-1}^{n-1}+\partial_{x}\phi_{-1}^{n-1}), \end{align*}$

$\begin{align*} G^{n-1, -1}=\,&[\mu^{n-1}-\lambda^{n-1}-V(\mathbf{x})-\beta_{0}\rho^{n-1}+\beta_{1}F_{z}^{n-1}]\phi_{-1}^{n-1}-\beta_{1}(\frac{\sqrt{6}}{2}F_{+}^{n-1}\phi_{0}^{n-1} +F_{-}^{n-1}\phi_{-2}^{n-1}) \\ & +\frac{\beta_{2}}{\sqrt{5}}A_{00}^{n-1}\bar{\phi_{1}}^{n-1} +\gamma[{\rm i}\partial_{y}(\phi_{-2}^{n-1}+\frac{\sqrt{6}}{2}\phi_{0}^{n-1})+\partial_{x}(\frac{\sqrt{6}}{2}\phi_{0}^{n-1}-\phi_{-2}^{n-1})], \\ G^{n-1, 0}=\,&[\mu^{n-1}-V(\mathbf{x})-\beta_{0}\rho^{n-1}]\phi_{0}^{n-1}-\frac{\sqrt{6}}{2}\beta_{1}(F_{+}^{n-1}\phi_{1}^{n-1}+F_{-}^{n-1}\phi_{-1}^{n-1})\\ &-\frac{\beta_{2}}{\sqrt{5}}A_{00}^{n-1}\bar{\phi_{0}}^{n-1}+\frac{\sqrt{6}}{2}\gamma[{\rm i}\partial_{y} (\phi_{-1}^{n-1}+\phi_{1}^{n-1})-\partial_{x}(\phi_{-1}^{n-1}-\phi_{1}^{n-1})], \\ G^{n-1, 1}=\,&[\mu^{n-1}+\lambda^{n-1}-V(\mathbf{x})-\beta_{0}\rho^{n-1}-\beta_{1}F_{z}^{n-1}]\phi_{1}^{n-1}-\beta_{1}(\frac{\sqrt{6}}{2}F_{-}^{n-1}\phi_{0}^{n-1} +F_{+}^{n-1}\phi_{2}^{n-1})\\ &+\frac{\beta_{2}}{\sqrt{5}}A_{00}^{n-1}\bar{\phi_{-1}}^{n-1} +\gamma[{\rm i}\partial_{y} (\phi_{2}^{n-1}+\frac{\sqrt{6}}{2}\phi_{0}^{n-1})-\partial_{x}(\frac{\sqrt{6}}{2}\phi_{0}^{n-1}-\phi_{2}^{n-1})], \\ G^{n-1, 2}=\,&[\mu^{n-1}+2\lambda^{n-1}-V(\mathbf{x})-\beta_{0}\rho^{n-1}-2\beta_{1}F_{z}^{n-1}]\phi_{2}^{n-1}-\beta_{1}F_{-}^{n-1}\phi_{1}^{n-1}\\ &-\frac{\beta_{2}}{\sqrt{5}}A_{00}^{n-1}\bar{\phi_{-2}}^{n-1}+\gamma({\rm i}\partial_{y} \phi_{1}^{n-1}-\partial_{x}\phi_{1}^{n-1}). \end{align*}$

稳定项因子 $\varepsilon^{n}$ 取为

$\begin{equation} \varepsilon^n = \frac{1}{2}(b^{n}_{\max}+b^{n}_{\min}), \end{equation}$

(3.3)

这里 $b^{n}_{\max}$ 及 $b^{n}_{\min}$ 表达式为

$b^{n}_{\max} = \max_{1\leq j \leq J-1}\max_{1\leq k \leq K-1} (V_{jk} + \beta_{0}\rho_{jk}^{n}),$

$b^{n}_{\min} = \min_{1\leq j \leq J-1}\min_{1\leq k \leq K-1} (V_{jk} + \beta_{0}\rho_{jk}^{n}).$

通过对 $\phi^{n-1,\ell}$ 进行快速离散傅里叶变换, 可得

$\begin{equation} \widehat{\phi_{p,q}^{n-1,\ell}}=\frac{1}{JK}\sum_{j=0}^{J-1}\sum_{k=0}^{K-1}\phi_{j,k}^{n-1,\ell}{\rm e}^ {-{\rm i}\mu_p(x_j-a)}{\rm e}^{-{\rm i}\mu_q(y_k-c)}, \end{equation}$

(3.4)

这里 $\mu_{p}=\frac{2p\pi}{b-a}$ , $\mu_{q}=\frac{2q\pi}{d-c}$ , $p=-J/2,-J/2+1,\cdots,J/2-1$ , $q=-K/2,-K/2+1,\cdots, K/2-1$ . 进而, 可得微分算子 $\nabla^{2}$ 的近似 $\nabla_{h}^{2}$ .

$D_{x}^{h}\phi_{j,k}^{n-1,\ell}={\rm i}\sum_{p=-J/2}^{J/2-1}\sum_{q=-K/2}^{K/2-1} \mu_{p}\widehat{\phi_{p,q}^{n-1,\ell}}{\rm e}^{{\rm i}\mu_p(x_j-a)}{\rm e}^{{\rm i}\mu_q(y_k-c)},$

$D_{y}^{h}\phi_{j,k}^{n-1,\ell}={\rm i}\sum_{p=-J/2}^{J/2-1}\sum_{q=-K/2}^{K/2-1}\mu_{q} \widehat{\phi_{p,q}^{n-1,\ell}}{\rm e}^{{\rm i}\mu_p(x_j-a)}{\rm e}^{{\rm i}\mu_q(y_k-c)},$

$\begin{equation} \nabla_{h}^{2}\phi^{n-1,\ell}_{j,k}=-\sum_{p=-J/2}^{J/2-1}\sum_{q=-K/2}^{K/2-1}(\mu_{p}^{2}+\mu_{q}^{2}) \widehat{\phi_{p,q}^{n-1,\ell}}{\rm e}^{{\rm i}\mu_p(x_j-a)}{\rm e}^{{\rm i}\mu_q(y_k-c)}. \end{equation}$

(3.5)

通过对 (3.1) 式的两边作快速傅里叶变换可得

$\begin{equation} \frac{\widehat{\phi_{pq}^{*,\ell}} - \widehat{\phi_{pq}^{n-1,\ell}}}{\Delta t}= -\left(\frac{\mu_{p}^{2}}{2} + \frac{\mu_{q}^{2}}{2} + \varepsilon^{n-1}\right)\widehat{\phi_{pq}^{\ast,\ell}} +\varepsilon^{n-1}\widehat{\phi_{pq}^{n-1,\ell}} +\widehat{G^{n-1,\ell}_{pq}}. \end{equation}$

(3.6)

化简得

$\begin{equation} \widehat{\phi_{pq}^{*,\ell}} = \frac{1}{1+\Delta t(\frac{\mu_{p}^{2}}{2} + \frac{\mu_{q}^{2}}{2}+\varepsilon^{n-1} )} \left(\widehat{\phi_{pq}^{n-1,\ell}} +\Delta t \varepsilon^{n-1}\widehat{\phi_{pq}^{n-1,\ell}} +\Delta t\widehat{G^{n-1, \ell}_{pq}} \right). \end{equation}$

(3.7)

通过对 (3.7) 式作逆快速傅里叶变换即得方程 (3.1) 的解.

4 数值实验

本章运用 GFLM 方法模拟自旋轨道耦合 Spin-2 BEC 在各参数下的基态. 对循环型体系 $(\beta_{1}>0)$ 和铁磁体系 ( $\beta_{1}<0)$ 两种情况, 初值的各分量函数皆取为

$\begin{equation*} \phi_{\ell}^0({\bf x})=\alpha_\ell^0\phi_{g}({\bf x}),\quad \ell=-2,-1,0,1,2, \end{equation*}$

其中 $\phi_g({\bf x})$ 为单组份 BEC 模型

${\rm i}\partial_{t}\psi({\bf x},t) =\left(-\frac{1}{2}\nabla^{2}+V({\bf x})+\beta_{0}|\psi({\bf x},t)|^{2}\right)\psi({\bf x},t)$

的基态或其近似 $\phi_{ho}({\bf x})=\frac{1}{\sqrt{\pi}}{\rm e}^{-(x^2+y^2)/2}$ . 除非特别说明, 本文取计算区域 $D=(-10,10)^2$ , 网格剖分数 $J=K=128$ , 势函数为 $V({\bf x})=0.5(x^2+y^2)$ .

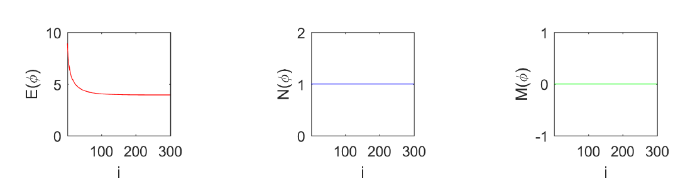
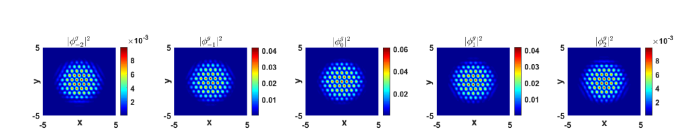
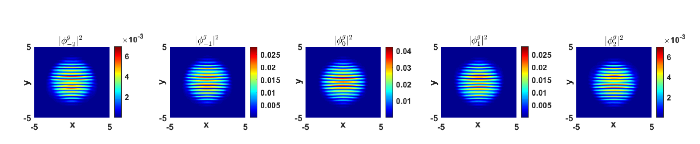
算例 1 (可行性测试) 取 $\beta_{0}=100$ , $\beta_{1}=1$ , $\beta_{2}=-2$ , 磁场量 $M=0$ , 自旋轨道耦合强度 $\gamma=0$ . 应用 GFLM 方法求该参数下的基态解.

图1 是 GFLM 方法模拟算例 1 基态解的结果. 观察可得: (1) 基态解分量 $\phi_{-\ell}^g=\phi_{\ell}^g (\ell=1,2)$ , 即分量呈对称出现, 这与理论结果是相符的, 事实上, 由自旋轨道耦合 Spin-2 BEC 满足的 CGPEs (1.1)-(1.3) 可知, 当总磁场量 $M=0$ 时, 将任意解的分量波函数 $\phi_{-\ell}$ 与 $\phi_{\ell}$ 互换所得的 $\rm CGPEs$ 保持不变, 因此基态解也满足 $\phi_{-\ell}^g=\phi_{\ell}^g (\ell=1,2)$ ; (2) 自旋轨道耦合强度 $\gamma=0$ 时, 基态解五个分量均呈圆形状.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 算例 1 中基态解的各分量模的平方

图2 表示计算过程中, 能量、总质量和总磁场量随迭代次数的变化情况. 观察可知: (1) 能量一直减少, 最后达到稳定状态; (2) 总质量 $N\equiv1$ , 说明总质量是守恒的; (3) 总磁场量 $M\equiv0$ , 说明总磁场量是守恒的. 事实上, 本算例及大量未展示的数值结果表明: 应用 GFLM 方法模拟自旋轨道耦合 Spin-2 BEC 的基态是可行的.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 算例 1 中能量( $E_{\phi}$ ), 总质量( $N_{\phi}$ ) 和总磁场量( $M_{\phi}$ )随迭代次数的变化图

算例 2 (循环型体系下结果) 取 $\beta_{0}=100, \beta_{1}=1, \beta_{2}=2, M=0$ , 依次计算自旋轨道耦合强度 $\gamma=1.5, \gamma=2, \gamma=2.3, \gamma=2.4, \gamma=3, \gamma=4$ 时的基态解.

图3-图8 是算例 2 中所得的具有循环型体系下自旋轨道耦合 Spin-2 BEC 基态. 观察可得: (1) 基态解分量 $\phi_{-\ell}^g$ 和 $\phi_{\ell}^g (\ell=1,2)$ 呈镜像对称; (2) 当磁场量 $M=0$ 时, 随着自旋轨道耦合强度 $\gamma$ 的增加, 基态解的图案由晶格图案变为竖条纹图案再变为晶格图案; (3) 当基态解分量出现晶格图案 (或竖条纹图案) 时, 稍微增大自旋轨道耦合强度 $\gamma$ 的值, 晶格 (或竖条纹) 数量增多.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 算例 2 中 $\gamma=1.5$ 时基态解各分量模的平方

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 算例 2 中 $\gamma=2$ 时基态解各分量模的平方

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 算例 2 中 $\gamma=2.3$ 时基态解各分量模的平方

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 算例 2 中 $\gamma=2.4$ 时基态解各分量模的平方

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 算例 2 中 $\gamma=3$ 时基态解各分量模的平方

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 算例 2 中 $\gamma=4$ 时基态解各分量模的平方

算例 3 (循环型体系下结果) 固定 $\beta_{0}=100, \beta_{1}=1, \beta_{2}=2$ , 依次计算 $M=1, \gamma=1.5$ 和 $M=1.2, \gamma=2$ 这两组参数下的基态解.

图9-图10 是算例 3 中所得自旋轨道耦合 Spin-2 BEC 的基态解. 观察可得: (1) $M\neq0$ 时, 基态解呈现的晶格图案或条纹图案发生扭曲; (2) 基态解分量 $\phi_{-\ell}^g$ 和 $\phi_{\ell}^g (\ell=1,2)$ 不呈镜像对称.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 算例 3 中 $M=1$ , $\gamma=1.5$ 时基态解各分量模的平方

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 算例 3 中 $M=1.2$ , $\gamma=2$ 时基态解各分量模的平方

由上可得: GFLM 方法可以有效模拟循环型体系下自旋轨道耦合 Spin-2 BEC 的基态解; 磁场量 $M=0$ 时, 随着自旋轨道耦合强度 $\gamma$ 的增大, 基态解可呈晶格图案和横条纹图案.

算例 4 (铁磁体系下结果) 取 $\beta_{0}=100, \beta_{1}=-1, \beta_{2}=-25, M=0$ 依次计算自旋轨道耦合强度 $\gamma=1.5, \gamma=2, \gamma=3.2, \gamma=3.3, \gamma=3.5, \gamma=4$ 时的基态解.

图11-图16 是算例 4 中所得自旋轨道耦合 Spin-2 BEC 的基态解. 观察可得: (1) 基态解分量 $\phi_{-\ell}^g$ 和 $\phi_{\ell}^g (\ell=1,2)$ 呈镜像对称; (2) 当磁场量 $M=0$ 时, 随着自旋轨道耦合强度 $\gamma$ 的增加, 基态分量出现竖条纹图案和横条纹图案; (3) 当基态解分量出现竖条纹图案 (或横条纹图案) 时, 稍微增大自旋轨道耦合强度 $\gamma$ 的值, 竖条纹 (或横条纹) 数量增多. 特别地, 在由竖条纹图案向横条纹图案转变的临界状态下出现斜向条纹图案.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 算例 4 中 $\gamma=1.5$ 时基态解各分量模的平方

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 算例 4 中 $\gamma=2$ 时基态解各分量模的平方

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 算例 4 中 $\gamma=3.2$ 时基态解各分量模的平方

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 算例 4 中 $\gamma=3.3$ 时基态解各分量模的平方

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 算例 4 中 $\gamma=3.5$ 时基态解各分量模的平方

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 算例 4 中 $\gamma=4$ 时基态解各分量模的平方

算例 5 (铁磁体系下结果) 固定 $\beta_{0}=100$ , $\beta_{1}=-1$ , $\beta_{2}=-25$ , 依次计算 $M=0.6, \gamma=1.5$ 和 $M=0.5, \gamma=2$ 这两组参数下的基态解.

图17-图18 是算例 5 中所得自旋轨道耦合强度的自旋轨道耦合 Spin-2 BEC 的基态解. 观察可得: (1) $M\neq0$ 时, 基态解完整的条纹图案发生扭曲; (2) 基态解分量 $\phi_{-\ell}^g$ 和 $\phi_{\ell}^g (\ell=1,2)$ 不呈镜像对称.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 算例 5 中 $M=0.6$ , $\gamma=1.5$ 时基态解各分量模的平方

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 算例 5 中 $M=0.5$ , $\gamma=2$ 时基态解各分量模的平方

由上可得: GFLM 方法可有效模拟铁磁体系下自旋轨道耦合 Spin-2 BEC 的基态解; 磁场量 $M=0$ 时, 随着自旋轨道耦合强度 $\gamma$ 的增大, 基态解可出现竖条纹, 斜条纹和横条纹图案.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Anderson

M H

, Ensher

J R

, Matthewa

M R

, et al.

Observation of Bose-Einstein condensation in a dilute atomic vapor

Science, 1995, 269: 198-201

PMID:17789847 [本文引用: 1]

A Bose-Einstein condensate was produced in a vapor of rubidium-87 atoms that was confined by magnetic fields and evaporatively cooled. The condensate fraction first appeared near a temperature of 170 nanokelvin and a number density of 2.5 x 10(12) per cubic centimeter and could be preserved for more than 15 seconds. Three primary signatures of Bose-Einstein condensation were seen. (i) On top of a broad thermal velocity distribution, a narrow peak appeared that was centered at zero velocity. (ii) The fraction of the atoms that were in this low-velocity peak increased abruptly as the sample temperature was lowered. (iii) The peak exhibited a nonthermal, anisotropic velocity distribution expected of the minimum-energy quantum state of the magnetic trap in contrast to the isotropic, thermal velocity distribution observed in the broad uncondensed fraction.

[2]

Antoine

, Levitt

, Tang

Efficient spectral computation of the stationary states of rotating Bose-Einstein condensates by preconditioned nonlinear conjugate gradient methods

Journal of Computational Physics, 2017, 343:92-109

[本文引用: 1]

[3]

Bao

, Cai

Mathematical models and numerical methods for spinor Bose-Einstein condensates

Communications in Computational Physics, 2018, 24: 899-965

[本文引用: 1]

[4]

Bao

, Du

Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow

SIAM Journal on Scientific Computing, 2004, 25: 1674-1697

DOI:10.1137/S1064827503422956 URL [本文引用: 1]

[5]

Bao

, Lim

Computing ground states of spin-1 Bose-Einstein condensates by the normalized gradient flow

SIAM Journal on Scientific Computing, 2008, 30 1925-1948

DOI:10.1137/070698488 URL [本文引用: 1]

[6]

Bao

, Tang

Ground state solution of Bose-Einstein condensate by directly minimizing the energy functional

Journal of Computational Physics, 2003, 187: 230-254

DOI:10.1016/S0021-9991(03)00097-4 URL [本文引用: 1]

[7]

Bao

, Wang

A mass and magnetization conservervative and energy-diminishing numerical method for computing ground state of spin-1 Bose-Einstein condensates

SIAM Journal on Numerical Analysis, 2007, 45(5): 2177-2200

DOI:10.1137/070681624 URL [本文引用: 1]

[8]

Bao

, Wang

, Markowich

P A

Ground, symmetric and central vortex states in rotating Bose-Einstein condensates

Communications in Mathematical Sciences, 2005, 3(1): 57-88

DOI:10.4310/CMS.2005.v3.n1.a5 URL [本文引用: 1]

[9]

Bose.

Plancks gesetz und lichtquantenhypothese

Zeitschrift fur Physik, 1924, 26: 178-181

DOI:10.1007/BF01327326 URL [本文引用: 1]

[10]

Bradley

C C

, Sackett

C A

, Tollett

J J

, Hulet

R G

Evidence of Bose-Einstein condensation in an atomic gas with attractive interaction

Physical Review Letters, 1995, 75: 1687-1690

[本文引用: 1]

[11]

Cai

, Liu

Efficient and accurate gradient flow methods for computing ground states of spinor Bose-Einstein condensates

Journal of Computational Physics, 2021, 433: 110183

DOI:10.1016/j.jcp.2021.110183 URL [本文引用: 3]

[12]

Davis

K B

, Mewes

M O

, Andrews

M R

, et al.

Bose-Einstein condensation in a gas of sodium atoms

Physical Review Letters, 1995, 75: 3969-3973

PMID:10059782 [本文引用: 1]

[13]

Einstein

Quantentheorie des einatomigen idealen gases

Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1924, 22: 261-267

[本文引用: 1]

[14]

Einstein

Quantentheorie des einatomigen idealen gases, zweite abhandlung

Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1925, 1: 3-14

[本文引用: 1]

[15]

T L

Spinor Bose condensates in optical traps

Physical Review Letters, 1998, 81: 742-745

DOI:10.1103/PhysRevLett.81.742 URL [本文引用: 1]

[16]

Kawaguchi

, Ueda

Spinor Bose-Einstein condensates

Physics Reports, 2012, 520: 253-381

DOI:10.1016/j.physrep.2012.07.005 URL [本文引用: 1]

[17]

Liu

, Cai

Normalized gradient flow with Lagrange multiplier for computing ground states of Bose-Einstein condensates

SIAM Journal on Scientific Computing, 2021, 43(1): B219-B242

DOI:10.1137/20M1328002 URL [本文引用: 2]

[18]

Lin

Y J

, Compton

R L

, Jimenez-Garcia

, et al.

Synthetic magmetic fields for ultracold neutral stoms

Nature, 2009, 462: 628-632

DOI:10.1038/nature08609 [本文引用: 1]

[19]

Lin

Y J

, Compton

R L

, Perry

A R

, et al.

Bose-Einstein condensates in a uniform light-induced vector potential

Physical Review Letters, 2009, 102: 130401

DOI:10.1103/PhysRevLett.102.130401 URL [本文引用: 1]

[20]

Lin

Y J

, Jimenez-Garcia

, Spielman

I B

A spin-orbit-coupled Bose-Einstein condensates

Nature, 2011, 471: 83-86

DOI:10.1038/nature09887 [本文引用: 1]

[21]

Stamper-Kurn

D M

, Andrews

M R

, Chikkatur

A P

, et al.

Optical confinement of a Bose-Einstein condensate

Physical Review Letters, 1998, 80: 2027-2030

DOI:10.1103/PhysRevLett.80.2027 URL [本文引用: 1]

[22]

Stamper-Kurn

D M

, Ueda

Spinor Bose gases: Symmetries, magnetism, and quantum dynamics

Review of Modern Physics, 2013, 85: 1191-1244

DOI:10.1103/RevModPhys.85.1191 URL [本文引用: 1]

[23]

Yuan

, Xu

, Tang

, Wang

The numerical study of the ground states of spin-1 Bose-Einstein condensates with spin-orbit-coupling

East Asian Journal on Applied Mathematics, 2018, 8(3): 598-610

DOI:10.4208/eajam URL [本文引用: 1]

Observation of Bose-Einstein condensation in a dilute atomic vapor

1995

... 玻色-爱因斯坦凝聚 (BEC) 被称为世界物质第五态, 是指玻色子在温度接近绝对零度时达到的物质状态. 它由玻色和爱因斯坦在 1924-1925 年预测^[9,13,14], 并于 1995 年首次在物理实验中实现^[1,10,12]. ...

Efficient spectral computation of the stationary states of rotating Bose-Einstein condensates by preconditioned nonlinear conjugate gradient methods

2017

... 近年已有大量的数值方法模拟 BEC 的基态. Bao 等早期采用直接最小化能量泛函法来求解基态^[6]. 随后, Bao 和 Du 提出了一种简单且广泛适用的方法, 即正规梯度流法^[4]来计算 BEC 的基态. 对于旋转单组份 BEC 模型, Bao 等采用向后欧拉有限差分离散的连续梯度流法^[8]研究了模型的基态, 对称态和中心涡态以及能量和化学势图. Antoine 和 Tang 等提出了效率更高的预条件共轭梯度法 (PCG)^[2]. ...

Mathematical models and numerical methods for spinor Bose-Einstein condensates

2018

... 对于旋量 BEC 的基态模拟, Bao 和 Wang 为 Spin-1 BEC 构造了连续梯度流并对其采用 Crank-Nicolson 有限差分进行离散^[7]. 随后, Bao 等利用离散正规梯度流法计算 Spin-1 和 Spin-2 BEC 的基态^[3,5], 其核心在于发掘投影系数间的隐含关系, 连同模型中的总质量和总磁场量守恒关系, 使得投影步骤所需的所有投影系数可被唯一确定. 此外, Cai 和 Liu 提出了模拟不带自旋轨道耦合项的 Spin-

$\mathcal{F}$

BEC 基态的带拉格朗日乘子的梯度流法^[11,17]. ...

Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow

2004

Computing ground states of spin-1 Bose-Einstein condensates by the normalized gradient flow

2008

$\mathcal{F}$

BEC 基态的带拉格朗日乘子的梯度流法^[11,17]. ...

Ground state solution of Bose-Einstein condensate by directly minimizing the energy functional

2003

A mass and magnetization conservervative and energy-diminishing numerical method for computing ground state of spin-1 Bose-Einstein condensates

2007

$\mathcal{F}$

BEC 基态的带拉格朗日乘子的梯度流法^[11,17]. ...

Ground, symmetric and central vortex states in rotating Bose-Einstein condensates

2005

Plancks gesetz und lichtquantenhypothese

1924

Evidence of Bose-Einstein condensation in an atomic gas with attractive interaction

1995

Efficient and accurate gradient flow methods for computing ground states of spinor Bose-Einstein condensates

2021

$\mathcal{F}$

BEC 基态的带拉格朗日乘子的梯度流法^[11,17]. ...

... 对于自旋轨道耦合旋量 BEC 模型, Yuan 等^[23] 提出了投影梯度流法计算自旋轨道耦合 Spin-1 BEC 的基态. 该方法采用空间二阶有限差分和时间 Grank-Nicolson 方法离散连续梯度流, 具有总质量、总磁场量守恒及能量递减的性质. 然而, 自旋轨道耦合 Spin-2 BEC 模型具有复杂的自旋交换项和自旋单线态项, 其基态解在自旋轨道耦合效应下具有复杂的基态相, 可呈现细密的条纹状和晶格状两种图案. 这些特点对模拟自旋轨道耦合 Spin-2 BEC 基态的数值算法在精度与效率方面提出了新的挑战. 目前, 关于自旋轨道耦合 Spin-2 BEC 基态模拟的数值结果十分有限. 本文将带拉格朗日乘子的梯度流算法^[11,17] 推广到自旋轨道耦合 Spin-2 BEC 的基态模拟. 该方法在每步迭代只需求解一个常系数椭圆方程(组), 易实施且效率高. ...

... 因此, 为唯一确定所有投影系数

$\alpha_{\ell}^{n} (\ell = -2,-1,0,1,2)$

, 还需得到另外三个关于投影系数的方程. 受文献^[11]中对

$(\alpha_{\ell}^{n})^2$

作泰勒展开思想的启发, 可得 ...

Bose-Einstein condensation in a gas of sodium atoms

1995

Quantentheorie des einatomigen idealen gases

1924

Quantentheorie des einatomigen idealen gases, zweite abhandlung

1925

Spinor Bose condensates in optical traps

1998

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

气体中产生了旋量 BEC, 其内部自旋自由度被激活^[21]. 在光阱中, 不同超精细态的粒子在空间中具有不同的角动量, 从而产生丰富的自旋结构. 自旋量子数为

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

+1 个分量的矢量波函数进行刻画^[15,16,22]. 特别地, 由于粒子自旋和粒子运动的相互影响会产生自旋轨道耦合 (SOC) 效应, 近年, Lin 等^[18,19,20] 在中性原子的 BEC 实验中, 成功诱导了自旋轨道耦合旋量 BEC. ...

Spinor Bose-Einstein condensates

2012

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

Normalized gradient flow with Lagrange multiplier for computing ground states of Bose-Einstein condensates

2021

$\mathcal{F}$

BEC 基态的带拉格朗日乘子的梯度流法^[11,17]. ...

Synthetic magmetic fields for ultracold neutral stoms

2009

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

Bose-Einstein condensates in a uniform light-induced vector potential

2009

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

A spin-orbit-coupled Bose-Einstein condensates

2011

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

Optical confinement of a Bose-Einstein condensate

1998

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

Spinor Bose gases: Symmetries, magnetism, and quantum dynamics

2013

... 在早期实验中, 玻色子在磁势阱中不能发生自旋. 1998 年, 利用光学偶极子阱, 人们首次在自旋

$^{23}\mathrm{Na}$

$\mathcal{F}$

(

$\mathcal{F}$

为正整数) 的 BEC, 被称为 Spin-

$\mathcal{F}$

BEC, 存在 2

$\mathcal{F}$

+1 个超精细态, 且旋量凝聚态可用 2

$\mathcal{F}$

The numerical study of the ground states of spin-1 Bose-Einstein condensates with spin-orbit-coupling

2018

〈

〉