1 引言
Saint-Venant方程属于一阶拟线性
对于双曲系统的边界控制问题, 关键是控制器设计和稳定性分析. 从已有文献来看, 稳定性分析方法通常有Lyapunov函数法, 频域法, Riemann不变量法, 反步法以及谱分析方法等[10,11,12,13,14]. 在控制工程实践中, PI控制器能够改善系统的稳态性能, 受到广大学者的广泛关注. 在文献[15]和[16]中, 相继研究了星形网络结构和级联网络结构的双曲偏微分系统的PI边界控制器的设计. 此外, 控制器的更详细设计可参见文献[17](第5章, 第7章). 在文献[18,19]中, 对于一类双曲守恒律偏微分系统, 提出了一种前馈边界控制方法来抑制量测扰动. 当受控系统受到显著的输入扰动时, 这种控制技术可以在影响系统输出之前进行测量和补偿.
众所周知, 在实际应用中, 系统控制器和传感器之间的通信不可避免地会产生时间延迟, 这有时可以提高受控系统的性能[20], 亦有可能导致控制性能下降, 甚至使原本稳定的系统变得不稳定[21,22]. 在文献[23,24]中,Suh和Bien首先设计了比例负延迟(PMD, Proportional Minus Delay)控制器, 并证明在传统控制器上增加时间延迟反而可以改善系统的性能. 然而, 文献[23,24]中给出的结果是基于近似分析和数值模拟的. 之后, Atay[25]将PMD控制器应用于单摆和倒立摆系统, 采用特征根分析方法给出了系统参数的稳定域, 并得出无论时滞取值如何, 合适选取反馈参数均可使系统达到渐近稳定. Hu[26]使用延迟位置反馈或延迟速度反馈或两者结合来镇定线性无阻尼振荡器的周期振动. 随后, Liu和Hu[27]提出了一种结合位置反馈和延迟位置反馈(PDP, Position feedback and Delayed Position feedback)的控制器, 以稳定一类多自由度线性无阻尼系统. 近年来, 时滞反馈亦被用于镇定PDE系统. 在文献[28]中, 通过使用反步法和Lyapunov函数法, 研究了输入端具有任意长延迟的反应扩散偏微分方程的指数稳定性. 在文献[29]中, 基于简化的Hayami扩散波模型, 建立了系统的PDP 反馈控制策略, 并利用Lyapunov函数法建立了闭环系统的指数稳定性. 然而, 据我们所知, 对于
本文致力于设计PDP边界控制器来镇定双曲型PDE系统, 该系统描述的是具有底部坡度和底部摩擦的渠道水流动力学. 本文的贡献是在输入端设计PDP 控制器, 并利用算子半群理论证明了系统的适定性. 然后通过构造合适的Lyapunov函数, 建立反馈参数和时滞值所满足的充分条件, 以保证闭环系统的指数稳定性. 本文的结构如下: 在第2节中, 利用一阶运输方程初值问题的解来描述PDP控制器中的时滞项, 得到了PDE-PDE耦合闭环系统, 并将其改写为抽象发展方程的形式. 第3节利用算子半群理论证明了系统的适定性. 在第4节中, 结合Lyapunov函数方法给出控制参数和时滞值的充分条件, 证明了闭环系统在
2 模型建立和PDP控制器设计
其中,
图1
假设系统(2.1)的稳态为
其中
其中
本文仅考虑亚临界流动状态的情形, 即
不妨设系统(2.4)的初始条件为
边界条件及控制器
其中, 参数
利用位置反馈和时滞位置反馈的线性组合设计控制器以保证闭环系统(2.4)-(2.8)的指数稳定性, 其中, 反馈参数
考虑到一阶运输方程初值问题
的解可以表示为
同理, 令
则闭环系统(2.4)-(2.8)可写为如下PDE-PDE耦合系统的形式
其中
在Hilbert状态空间
中, 定义内积
其中
那么, 在Hilbert状态空间
其中
3 系统(2.17)的适定性
为了后续计算方便, 不失一般性, 在本节令
定理3.1 设算子
证 对于
即
由(3.2)式的前两个方程可得
进而
再将(3.4)式代入(3.2)式的第一个方程可得
因此, 由一阶线性常微分方程的通解公式得
其中
另外, 由(3.6)式可得
故结合(3.7)和(3.8)式, 有
不妨记
于是当
因此, 由Sobolve嵌入定理可知,
4 系统(2.12)的指数稳定性
本节致力于构建一个合适的Lyapunov函数来分析系统(2.12)的指数稳定性.
定义4.1 如果存在正常数
则闭环系统(2.12)在
定理4.1 假定参数
则闭环系统(2.12)是指数稳定的.
证 构造Lyapunov候选函数
其中,
且
其中
将(2.12)式中的边界条件代入
显然, 当参数满足条件
时, 必有
为使
即各阶顺序主子式均大于0
显然条件(4.9)(a)成立. 对于条件(4.9)(b), 若选择参数
考虑到
因此当
于是(4.9)(b)成立.
综上可得, 必存在正常数
注4.1 若选择如下Lyapunov候选函数
即(4.2)式中
5 系统算子的谱分析
在这一节, 旨在分析系统算子
即
类似于文献[定理3]的证明, 易得如下结论成立.
定理5.1 设
其中
此外, 对应的特征函数
其中
注5.1 特征值的渐近表达式(5.2)表明, 特征值的实部趋于某一常数, 虚轴不是特征值的渐近线. 此外, 基于特征函数的渐近表达式(5.4), 可知Riesz基性质和谱确定性增长条件成立, 进而结合系统的耗散性也可建立系统(2.17)的指数稳定性, 可参考文献[31].
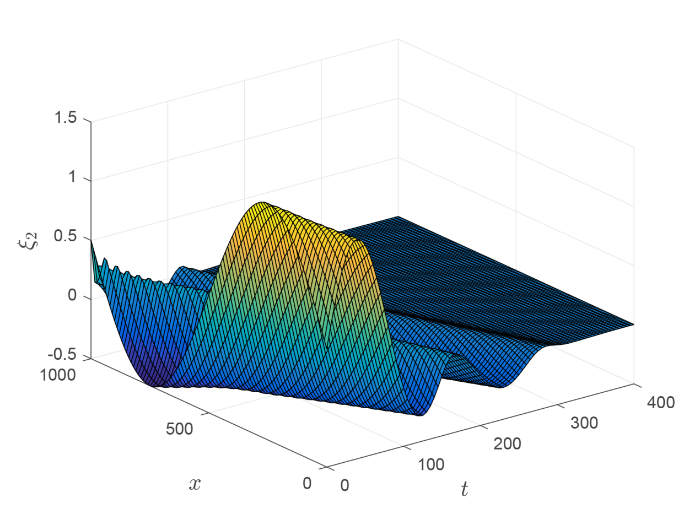
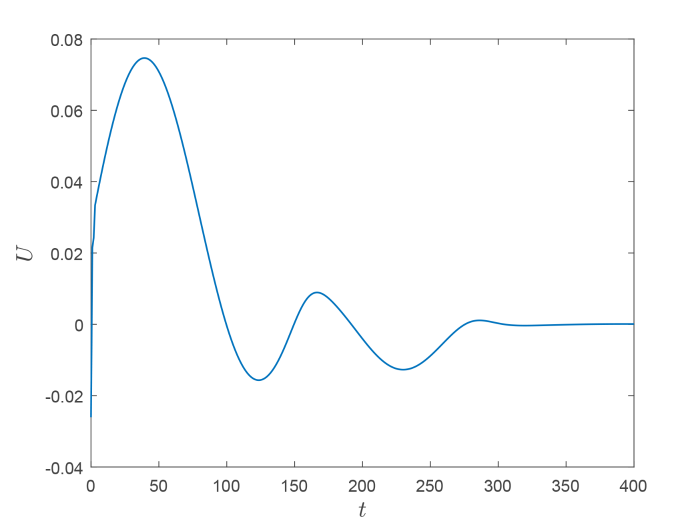
6 数值模拟
在这一节, 对于由 Saint-Venant 方程 (2.1) 描述的具有底部坡度和摩擦的单渠道系统进行数值仿真, 参数如下: 渠道长度
计算得稳态水深和流速分别是
取
满足
图2
图3
图4
7 结论
本文研究了由Saint-Venant方程描述的具有非零底部坡度和底部摩擦的单渠道系统的PDP边界控制器设计. 首先通过线性化手段和Riemann坐标变换将系统重构, 得到一类
参考文献
Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations
DOI:10.1016/j.conengprac.2004.12.010 URL [本文引用: 1]
Boundary control of open channels with numerical and experimental validations
DOI:10.1109/TCST.2008.919418 URL [本文引用: 1]
Stability of linear density-flow hyperbolic systems under PI boundary control
DOI:10.1016/j.automatica.2014.12.025 URL [本文引用: 1]
PI boundary control of linear hyperbolic balance laws with stabilization of ARZ traffic flow models
DOI:10.1016/j.sysconle.2018.11.005 URL [本文引用: 1]
Stability and Boundary Stabilization of 1-D Hyperbolic Systems
Backstepping boundary stabilization and state estimation of a
Boundary control of hyperbolic conservation laws using a frequency domain approach
DOI:10.1016/j.automatica.2008.09.022 URL [本文引用: 1]
Exponential stability of PI control for Saint-Venant equations with a friction term
DOI:10.4310/MAA.2019.v26.n2.a1 URL [本文引用: 1]
A strict Lyapunov function for boundary control of hyperbolic systems of conservation laws
DOI:10.1109/TAC.2006.887903 URL [本文引用: 1]
A quadratic Lyapunov function for Saint-Venant equations with arbitrary friction and space-varying slope
DOI:10.1016/j.automatica.2018.10.035 URL [本文引用: 1]
Feedback stabilization for a scalar conservation law with PID boundary control
Boundary feedback stabilization and Riesz basis property of a 1-d first order hyperbolic linear system with
DOI:10.1016/j.jde.2008.08.010 URL [本文引用: 1]
Boundary PI controllers for a star-shaped network of
Output regulation for a cascaded network of
DOI:10.1016/j.automatica.2018.01.010 URL [本文引用: 1]
PID Controllers: Theory, Design, and Tunning
Robust feedforward boundary control of hyperbolic conservation laws
DOI:10.3934/nhm.2007.2.717 URL [本文引用: 1]
Feedforward boundary control of
DOI:10.1016/j.ejcon.2020.11.002 URL [本文引用: 1]
Analog study of dead-beat posicast control
DOI:10.1109/TAC.1958.1104844 URL [本文引用: 1]
Some problems of delayed feedback control
Proportional minus delay controller
DOI:10.1109/TAC.1979.1102024 URL [本文引用: 2]
Use of time-delay actions in the controller design
DOI:10.1109/TAC.1980.1102347 URL [本文引用: 2]
Balancing the inverted pendulum using position feedback
Using delayed state feedback to stabilize periodic motions of an oscillator
DOI:10.1016/j.jsv.2003.07.006 URL [本文引用: 1]
Stabilization of linear undamped systems via position and delayed position feedbacks
DOI:10.1016/j.jsv.2007.11.001 URL [本文引用: 1]
Control of an unstable reaction-diffusion PDE with long input delay
DOI:10.1016/j.sysconle.2009.08.006 URL [本文引用: 1]
一类扩散波方程的PDP反馈控制和稳定性分析
The PDP feedback control and stability analysis of a diffusive wave equation
On Lyapunov stability of linearised Saint-Venant equations for a sloping channel
DOI:10.3934/nhm.2009.4.177 URL [本文引用: 2]
The spectral analysis and exponential stability of a 1-d
DOI:10.1007/s12555-021-0507-0 [本文引用: 1]