1 引言
本文研究了拟线性两点边值问题
正解的确切个数和分歧图, 其中
2019 年, Huang[9] 研究了当非线性项满足条件
值得注意的是, 上述文献没有考虑当非线性项
(H1)
(H2)
假设
(C1) 存在
(C2) 存在
得出结果
定理1.1 假设非线性项
(i) 当
(ii) 当
(iii) 当
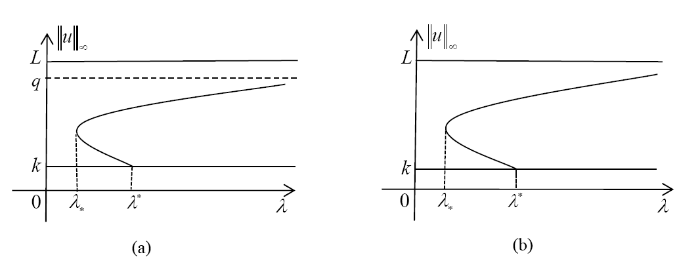
图1
定理1.2 假设非线性项
(i) 当
(ii) 当
(iii) 当
2 引理及主要结果证明
为了证明定理 1.1-1.2, 首先来介绍时间映像方法, 详见文献 [2]. 定义了问题 (1.1) 的时间映像公式, 对任意的
其中
为了方便, 定义
注2.1 为了保证对任意的
易得当
引理 2.1[13] 假设非线性项
引理 2.2[13] 假设非线性项
引理 2.3[13] 假设非线性项
引理 2.4 假设非线性项
证 因为对任意的
这表明对任意的
对任意的
从 (2.1) 式进一步得
这表明对任意的
容易得出
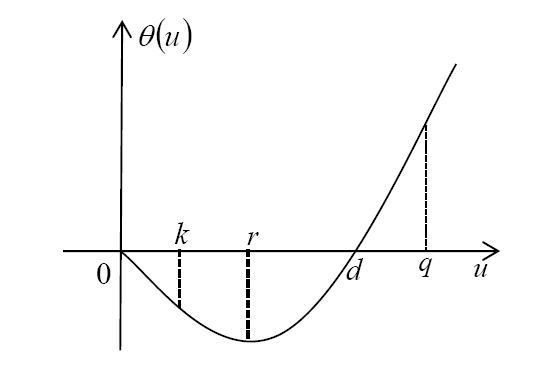
图2
注意到存在
更进一步得到
和
因此,
证明完毕.
引理 2.5 假设非线性项
证 易知
令
再令
引理 2.6 假设非线性项
证 令
通过计算,
因为
因此,
由于对任意的
应用同样的证明, 可得对任意的
引理 2.7 假设非线性项
证 因为对任意的
证明完毕.
引理 2.8 假设非线性项
证 由
容易看出
这表明对任意的
对任意的
因此, 存在
所以, 进一步得
证明完毕.
下面证明定理 1.1.
证 根据时间映像的定义, 研究对任意固定的
通过引理 2.3, 可知
这表明存在
因此, 结合引理 2.2 和引理 2.3-2.8, 得到了对任意的
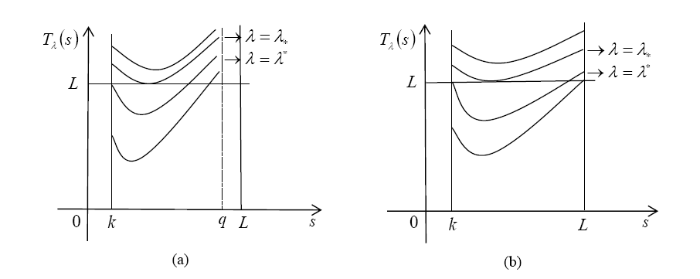
图3
由图可知, 存在
证明完毕.
下面证明定理 1.2.
证 根据时间映像的定义, 研究对任意固定的
通过引理 2.3, 可知
这表明存在
因此, 结合引理 2.2 和引理 2.3-2.6, 得到了对任意的
由图可知, 存在
3 三个例子
例 3.1
通过计算,
例 3.2
通过计算,
例 3.3
通过计算,
参考文献
Mathematical Analysis of Some Differential Models Involving the Euclidean or the Minkowski Mean Curvature Operator
Bifurcation curves and exact multiplicity of positive solutions for Dirichlet problems with the Minkowski-curvature equation
Some problems in the theory of quasilinear equations
Global bifurcation diagrams for Liouville-Bratu-Gelfand problem with Minkowski-curvature operator
DOI:10.1007/s10884-021-09982-4 [本文引用: 1]
Exact multiplicity and bifurcation curves of positive solutions of a one-dimensional Minkowski-curvature problem and its application
DOI:10.3934/cpaa.2018061 URL [本文引用: 1]
Classifification and evolution of bifurcation curves for the one-dimensional Minkowski-curvature problem and its applications
DOI:10.1016/j.jde.2018.01.021 URL [本文引用: 1]
Global bifurcation and exact multiplicity of positive solutions for the one-dimensional Minkowski-curvature problem with sign-changing nonlinearity
DOI:10.3934/cpaa.2019147 URL [本文引用: 1]
Bifurcation diagrams of positive solutions for one-dimensional Minkowski-curvature problem and its applications
Bifurcation curves of positive solutions for the Minkowski-curvature problem with cubic nonlinearity
Bifurcation diagrams and exact multiplicity of positive solutions of one-dimensional prescribed mean curvature equation in Minkowski space