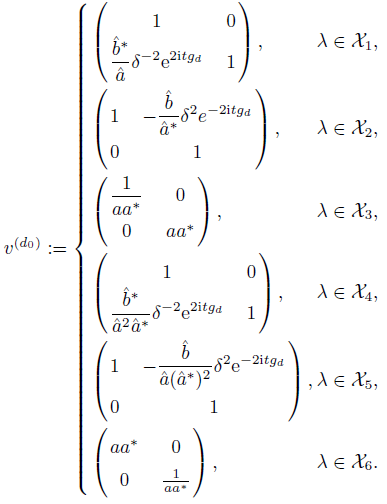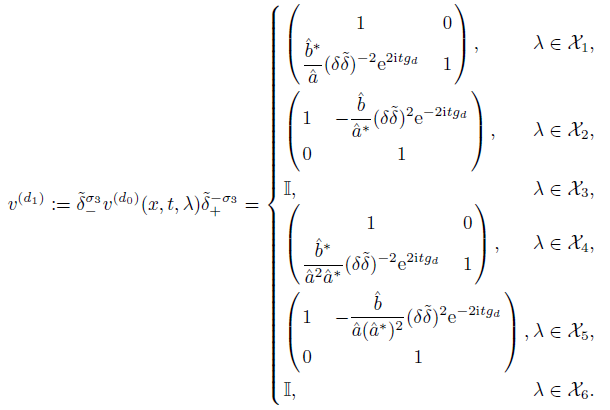1 引言
(1.1) $\begin{matrix}{\rm i}u_{t}+\frac{1}{2}u_{xx}+|u|^{2}u=0\end{matrix}$
在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程
(1.2) $\begin{matrix}{\rm i}u_{t}+\frac{1}{2}u_{xx}+|u|^{2}u+2\beta^{2}|u|^4u-2{\rm i}\beta(|u|^2)_{x}u=0,~~x \in \mathbb{R},~t\geq 0,\end{matrix}$
该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能.
反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] .
虽然现已存在 KE 方程解的长时间渐进性的一些工作[38 ⇓ ⇓ -41 ] , 但大都关于初边值条件为零或简单非零边值条件的情况. 因此, 本文利用非线性速降法探索在阶跃振荡背景下聚焦 KE 方程(1.2)解的长时间渐进性. 当 $x\rightarrow\pm\infty$
(1.3) $\begin{matrix}u(x,0)=u_{0}(x)\sim\left\{\begin{array}{c} A_{1}{\rm e}^{{\rm i}(\mu_{1}x+\theta_{1})},~~x\rightarrow -\infty, \\ A_{2}{\rm e}^{{\rm i}(\mu_{2}x+\theta_{2})},~~x\rightarrow +\infty, \end{array} \right.\end{matrix}$
其中 $\{A_{j},\mu_{j},\theta_{j}\}_{1}^{2}$ $A_{j}>0$ $j=1, 2$ .
为完善柯西问题(1.2)-(1.3), 边值条件需满足
(1.4) $\begin{matrix}\int_{0}^{(-1)^{j}\infty}|u(x,t)-u_{0j}(x,t)|{\rm d}x<\infty,~~\forall~t\geq0,~j=1,2,\end{matrix}$
其中, $u_{0j}(x,t)$
(1.5) $\begin{matrix}u_{0j}(x,t)=A_{j}{\rm e}^{{\rm i}(\theta_{j}+\mu_{j}x+\omega_{j}t)},~~\omega_{j}:=A_{j}^{2}-\frac{1}{2}\mu_{j}^{2}+2\beta^{2} A_{j}^{4},~~j=1,2.\end{matrix}$
(2) 假设存在某一紧集, 使得初值 $u_{0}(x)$
即存在 $B > 0$ $x < -B$ $u_{0}(x)=u_{01}(x,0)$ $x > B$ $u_{0}(x)=u_{02}(x,0)$ .
本节将给出两条重要定理. 在第2节, 主要介绍了反散射变换法和基本的 Riemann-Hilbert 问题, 这是进行一系列推导的基础. 根据 $\tilde{\mu}_{1}\neq \tilde{\mu}_{2}$ $\tilde{\mu}_{2}< \tilde{\mu}_{1}$ ) 和激波情况 ($\tilde{\mu}_{2}> \tilde{\mu}_{1}$ ). 这两种情况都值得研究. 在第3节, 针对稀疏情况, 将上半平面划分为平面波区域、椭圆波区域以及慢衰减区域, 并分别计算了这三个区域的渐进解.在第4节, 讨论了激波的情况, 利用依赖于亏格为3的 黎曼曲面的超椭圆函数描述了解的长时间渐进性. 最后, 针对所研究问题给出一些结论并引发讨论.
定理 1.1 当 $\tilde{\mu}_{2}< \tilde{\mu}_{1}$
$\bullet$ $\xi<-2\tilde{\mu}_{1}-2\sqrt{2}A_{1}$ $\xi>-2\tilde{\mu}_{2}+2\sqrt{2}A_{2}$
(1.6) $\begin{matrix}u(x,t)&=&{\rm e}^{-2{\rm i}\beta\int_{x}^{+\infty}\left(|u(y,t)|^{2}-A_{j}^{2}\right){\rm d}y}A_{j}{\rm e}^{{\rm i}[\mu_{j}x+(A_{j}^{2}-\frac{\mu_{j}^{2}}{2}+2\beta^{2}A_{j}^{4})t+\phi_{j}(\xi)]}\\&&+O\left(t^{-\frac{1}{2}}\right),~~(-1)^{j}\xi \gg 0,~j=1, 2,\end{matrix}$
其中, $\phi_{1}(-\infty)=\theta_{1}$ $\phi_{2}(+\infty)=\theta_{2}$ .
$\bullet$ $-2\tilde{\mu}_{1}-2\sqrt{2}A_{1}<\xi<-2\tilde{\mu}_{1}$ $-2\tilde{\mu}_{2}<\xi<-2\tilde{\mu}_{2}+2\sqrt{2}A_{2}$
(1.7) $ \begin{matrix}u(x, t)&=&{\rm e}^{-2{\rm i}\beta\int_{x}^{+\infty}\left(|u(y,t)|^{2}-A_{j}^{2}\right){\rm d}y}\\&&\cdot(A_{j}+{\rm Im}\beta(\xi))\frac{\Theta\left(\frac{F_{j}t}{2\pi}+\frac{f_{j}}{2\pi}+\chi_{j}-U_{\infty}+b_{j}\right)\Theta\left(U_{\infty}+b_{j}\right)}{\Theta\left(\frac{F_{j}t}{2\pi}+\frac{f_{j}}{2\pi}+\chi_{j}+U_{\infty}+b_{j}\right)\Theta\left(-U_{\infty}+b_{j}\right)} \\&&\cdot{\rm e}^{{\rm i}[\mu_{j}x+(A_{j}^{2}-\frac{\mu_{j}^{2}}{2}+2\beta^{2}A_{j}^{4}+2g(\infty))t+2\hat{G}(\infty)+{\rm e}^{{\rm i}\phi_{j}}]}+O\left(t^{-\frac{1}{2}}\right),~~j=1,2,\end{matrix}$
其中, $b_{j}$ $f_{j}$ $\Theta(\lambda)$ $F_{j}$ $\chi_{j}$ $U_{\infty}$ $g(\infty)$ $\hat{G}(\infty)$
$\bullet$ $-2\tilde{\mu}_{1}<\xi<-2\tilde{\mu}_{2}$
(1.8) $ \begin{matrix}u(x,t)={\rm e}^{-2{\rm i}\beta\int_{x}^{+\infty}\left(|u(y,t)|^{2}-A_{j}^{2}\right){\rm d}y}b_{0}(\xi)t^{-1/2}{\rm e}^{{\rm i}\left[b_{1}(\xi)t+b_{2}(\xi)\log t+b_{3}(\xi)\right]}+o\left(t^{-\frac{1}{2}}\right),\end{matrix}$
其中 $b_{i}$ $i=0, 1, 2, 3$
定理 1.2 当 $\tilde{\mu}_{2}> \tilde{\mu}_{1}$ ${\cal I}$ ${\cal I}=(\xi_{1},\xi_{2})$ . 对于任意 $\xi\in{\cal I}$ $t\rightarrow\infty$ ${\cal I}$
(1.9) $\begin{matrix}u(x,t)={\rm e}^{-2{\rm i}\beta\int_{x}^{+\infty}\left(|u(y,t)|^{2}-A_{j}^{2}\right){\rm d}y}\left(E_{0}(\xi)+E_{1}(\xi)t^{-1/2}\right)+O\left(t^{-1}\ln t\right),\end{matrix}$
这里误差项关于 $\xi$ $E_{i}$ $i=0, 1$
注 1.1 众所周知, 聚焦 KE 方程(1.2)与 NLS 方程(1.1)的 Lax 对形式满足以下关系式
其中, $\tilde{U}$ $\tilde{V}$
(1.10) $\begin{matrix}u=q{\rm e}^{2{\rm i}\beta\int|q|^2{\rm d}x}.\end{matrix}$
这似乎可以从 NLS 方程的 Lax 对出发, 求得势函数 $q(x,t)$ $u(x,t)$ . 然而, 作为创新点之一, 本文直接基于聚焦 KE 方程的 Lax 对, 通过构造并求解相应的 Riemann-Hilbert 问题最终得到解的长时间渐进性. 更重要的是, 有效地避免了求解复杂的积分, 大大缩减了计算量.
2 反散射变换法和 Riemann-Hilbert问题
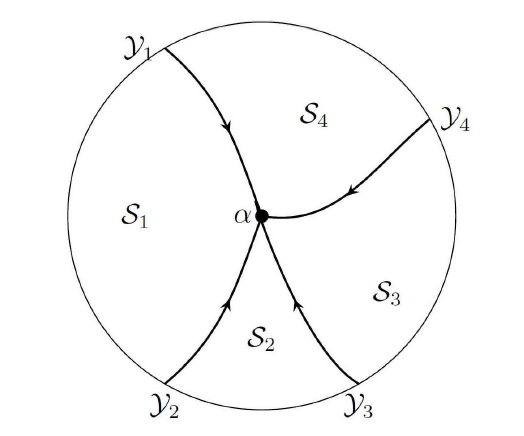
令 $\Gamma_{j}=[\bar{C}_{j},C_{j}]$ $C_{j}:= \tilde{\mu}_{j}+{\rm i}A_{j}$ $\tilde{\mu}_{j}:=-\frac{\mu_{j}}{2}+\beta A_{j}^{2}$ $j=1,2$ . 进而 $\Gamma_{j}=\{\tilde{\mu}_{j}+{\rm i}a|~|a|\leq A_{j}\}$ $\Gamma= \mathbb{R} \cup\Gamma_{1}\cup\Gamma_{2}$ .
由 $\tilde{\mu}_{1}\neq \tilde{\mu}_{2}$ $\tilde{\mu}_{2}< \tilde{\mu}_{1}$ ) 和激波情况 ($\tilde{\mu}_{2}> \tilde{\mu}_{1}$ ) , 如图2.1 所示.
图2.1
图2.1
基本的 Riemann-Hilbert 问题的轮廓线 $\Gamma$
记上下复半平面分别为开集 ${\Bbb C}^{+}=\{{\rm Im} \lambda>0\}$ ${\Bbb C}^{-}=\{{\rm Im} \lambda<0\}$ $\overline{{\Bbb C}}={\Bbb C}\cup\{\infty\}$ . 主分支的对数形式为 $\ln \lambda=\ln |\lambda|+{\rm i}\arg \lambda$ $\arg \lambda \in (-\pi,\pi]$ .
除非另有说明, 本文将使用 $z^{\alpha}={\rm e}^{\alpha \ln z}$ $f(\lambda)$ $f^{\ast}(\lambda):=\overline{f(\bar{\lambda})}$ . 此外, 边值的左右极限分别用下标 $+/-$
在以 $\Gamma$ $\overline{{\Bbb C}}$ $P$ . 由所有函数 $f(\lambda)$ $\dot{E}^{2}(P)$
$\bullet$ $P_{j}$ $P_{j}$ $\{B_{n}\}_{1}^{\infty}$ $B_{n}$ $P_{j}$ $\sup_{n\geq1}\|f\|_{L^{2}(B_{n})}<\infty$ .
$E^{\infty}(P)$ $P\rightarrow{\Bbb C}$
在 $L^{2}$ - 范数[42 ,43 ] 意义下, 定义 Riemann-Hilbert 问题
(2.1) $\begin{matrix}\left\{\begin{array}{c} n\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus\Gamma),~~~~~~~~~~~~ \\ n_{+}(\lambda)=n_{-}(\lambda)J(\lambda), ~\lambda\in \Gamma. \end{array}\right.\end{matrix}$
在复共轭条件下, 由于所有的跳跃曲线均不变, 故跳跃矩阵满足
(2.2) $\begin{matrix}J\equiv J(\lambda)=\left\{\begin{array}{c} \sigma_{2}J^{\ast}\sigma_{2},~~~~~~\lambda\in \Gamma\setminus\mathbb{R}, \\ \sigma_{2}(J^{\ast})^{-1}\sigma_{2},~~\lambda\in \Gamma\cap\mathbb{R}. \end{array}\right.\end{matrix}$
由 Riemann-Hilbert 问题(2.1)解的唯一性可知
(2.3) $\begin{matrix}n=\sigma_{2}n^{\ast}\sigma_{2},~~\lambda\in {\Bbb C}\setminus\Gamma.\end{matrix}$
(2.4) $\begin{matrix}\left\{\begin{array}{c} \Phi_{x}(x,t,\lambda)=X(x,t,\lambda)\Phi(x,t,\lambda), \\ \Phi_{t}(x,t,\lambda)=T(x,t,\lambda)\Phi(x,t,\lambda), \end{array} \right.\end{matrix}$
这里 $u(x,t)=u_{0j}(x,t)$ $j=1, 2$
鉴于 Riemann-Hilbert 问题在反散射变换中发挥着重要的作用, 很自然通过构造合适的 Riemann-Hilbert 问题来求解原柯西问题.
在 ${\Bbb C} \setminus \Gamma_{j}$ $j=1, 2$
(2.5) $\begin{matrix}\left\{\begin{array}{ll} U_{j}(\lambda)=\left[(\lambda+\frac{\mu_{j}}{2}-\beta A_{j}^{2})^{2}+A_{j}^{2}\right]^{\frac{1}{2}},\\[3mm] V_{j}(\lambda)=\left(\lambda-\frac{\mu_{j}}{2}+\beta A_{j}^{2}\right)U_{j}(\lambda),\\[3mm] \nu_{j}(\lambda)=\left(\frac{2\lambda+\mu_{j}-2\beta A_{j}^{2}-2{\rm i}A_{j}}{2\lambda +\mu_{j}-2\beta A_{j}^{2}+2{\rm i}A_{j}}\right)^{\frac{1}{4}},\\[5mm] \zeta_{j}(\lambda)=\left( \begin{array}{cc} \frac{1}{2}(\nu_{j}+\frac{1}{\nu_{j}}) & \frac{1}{2}{\rm e}^{{\rm i}\theta_{j}}(\nu_{j}-\frac{1}{\nu_{j}}) \\[3mm] \frac{1}{2}{\rm e}^{-{\rm i}\theta_{j}}(\frac{1}{\nu_{j}}-\nu_{j}) & \frac{1}{2}(\nu_{j}+\frac{1}{\nu_{j}}) \end{array} \right). \end{array} \right.\end{matrix}$
当 $\lambda\rightarrow\infty$
进一步地, 构造满足 Lax 对(2.4)的背景解
(2.6) $\begin{matrix}\Phi_{0j}(x,t,\lambda)&:=&{\rm e}^{\frac{{\rm i}}{2}(\mu_{j}x+\omega_{j}t)\sigma_{3}}M_{j}(\lambda){\rm e}^{-{\rm i}U_{j}\left[x+(\lambda-\frac{\mu_{j}}{2}+\beta A_{j}^{2})t\right]\sigma_{3}},\\M_{j}(\lambda)&:=&{\rm e}^{{\rm i}\frac{\theta_{j}}{2}\hat{\sigma}_{3}}\zeta_{j}(\lambda),~~j=1,2,\end{matrix}$
其中 ${\rm e}^{a\hat{\sigma}}{\cal A}={\rm e}^{a\sigma}{\cal A}{\rm e}^{-a\sigma}$ . $\omega_{j}$ $U_{j}$
对于 $\lambda\in {\Bbb C}\setminus\Gamma_{j}$ $M_{j}$ $\Phi_{0j}$
由 $\Gamma_{j}$ $\lambda\in\Gamma_{j}$ $\nu_{j+}(\lambda)={\rm i}\nu_{j-}(\lambda)$ .
解析函数 $M_{j}$ $j = 1, 2$
(2.7) $\left\{\begin{array}{l}M_{j} \in \mathbb{I}+\dot{E}^{2}\left(\mathbb{C} \backslash \Gamma_{j}\right), \\ M_{j+}(\lambda)=M_{j-}(\lambda)\left(\begin{array}{cc}0 & \mathrm{ie}^{\mathrm{i} \theta_{j}} \\ \mathrm{ie}^{-\mathrm{i} \theta_{j}} & 0\end{array}\right), \lambda \in \Gamma_{j}\end{array}\right.$
假设 $u(x,t)$
(2.8) $\begin{matrix}\Phi_{j}(x,t,\lambda):=T_{j}(x,t,\lambda){\rm e}^{-{\rm i}(U_{j}x+V_{j}t)\sigma_{3}},\end{matrix}$
其中 $U_{j}$ $V_{j}$ $T_{j}$ $j=1,2$
(2.9) $\begin{matrix}T_{j}(x,t,\lambda)&=&{\rm e}^{\frac{{\rm i}}{2}(\mu_{j}x+\omega_{j}t)\sigma_{3}}{\rm e}^{{\rm i}\frac{\theta_{j}}{2}\hat{\sigma}_{3}}\zeta_{j}(\lambda)\\&&+\int_{(-1)^{j}\infty}^{x}\Phi_{0j}(x,t,\lambda)\Phi_{0j}^{-1}(y,t,\lambda)\Delta Q_{0j}(y,t)T_{j}(y,t,\lambda){\rm e}^{-{\rm i}U_{j}(y-x)\sigma_{3}}{\rm d}y,\end{matrix}$
这里 $\Delta Q_{0j}=Q-Q_{0j}$ .
结合方程(2.8)和(2.9), Jost 解的 Volterra 积分形式为
(2.10) $\begin{equation}\Phi_{j}(x,t,\lambda)=\Phi_{0j}(x,t,\lambda)+\int_{(-1)^{j}\infty}^{x}\Phi_{0j}(x,t,\lambda)\Phi_{0j}^{-1}(y,t,\lambda)\Delta Q_{0j}(y,t)\Phi_{j}(y,t,\lambda){\rm d}y,\end{equation}$
其中 $\Phi_{0j}(x,t,\lambda)$ $j=1,2$
接下来, 分析矩阵 $T_{j}$ $j=1,2$
命题 2.1 记 $T^{(i)}_{j}$ $T_{j}$ $i$ $T_{1}^{(1)}$ $T_{1}^{(2)}$ ${\Bbb C}^{+}\setminus\Gamma_{1}$ ${\Bbb C}^{-}\setminus\Gamma_{1}$ $\Gamma_{1}$ $T_{2}^{(2)}$ $T_{2}^{(1)}$ ${\Bbb C}^{+}\setminus\Gamma_{2}$ ${\Bbb C}^{-}\setminus\Gamma_{2}$ $\Gamma_{2}$
当 $\lambda\in \Gamma_{1}\cup\Gamma_{2}$ $M_{j}$ $U_{j}$ $V_{j}$ $\Phi_{0j}$ $M_{j\pm}$ $U_{j\pm}$ $V_{j\pm}$ $\Phi_{0j\pm}$ $\Phi_{j\pm}(x,t,\lambda)$ $T_{j\pm}$ $T_{j\pm}$ $M_{j\pm}$ $U_{j\pm}$ $\Phi_{0j\pm}$ $T_{j\pm}$ $\Phi_{j\pm}$
由于 Jost 解 $\Phi_{j}(x, t, \lambda)$ $j=1,2$ $x$ $t$ $S(\lambda)$
(2.11) $\begin{equation}\Phi_{2}(x, t,\lambda)=\Phi_{1}(x, t, \lambda)S(\lambda),~\lambda \in \mathbb{R},~\lambda\neq \tilde{\mu}_{1}, \tilde{\mu}_{2}.\end{equation}$
根据 $\Phi_{j}(x, t, \lambda)$
由命题 2.1 可知, $a(\lambda)$ $a^{\ast}(\lambda)$ ${\Bbb C}^{+} \setminus (\Gamma_{1}\cup\Gamma_{2})$ ${\Bbb C}^{-} \setminus (\Gamma_{1}\cup\Gamma_{2})$ $\Gamma_{1}\cup\Gamma_{2}$
当(2.11)式中 $t=0$ $a(\lambda)$ $b(\lambda)$ $u_{0}(x)$
接下来, 介绍基本的 Riemann-Hilbert 问题.
(2.12) $\begin{matrix}n(x, t, \lambda):=\left\{\begin{array}{ll} \left(a^{-1}\Phi_{1}^{(1)}~~\Phi_{2}^{(2)}\right){\rm e}^{{\rm i} \lambda(x+\lambda t)\sigma_{3}},&\lambda\in {\Bbb C}^{+}, \\[2mm] \left(\Phi_{2}^{(1)}~~\Phi_{1}^{(2)}(a^{\ast})^{-1}\right) {\rm e}^{{\rm i}\lambda(x+\lambda t)\sigma_{3}}, &\lambda\in {\Bbb C}^{-}, \end{array}\right.\end{matrix}$
这里, $\Phi_{j}(x,t,\lambda)$ $j=1,2$ $n(x, t, \lambda)$ $u_{0}(x)$
矩阵函数 $n(x,t,\lambda)$
(2.13) $\begin{matrix}J(x,t,\lambda)={\rm e}^{-{\rm i}\lambda(x+\lambda t)\hat{\sigma}_{3}}J_{0}(\lambda).\end{matrix}$
其中 $J_{0}(\lambda)$ $n(x,t,\lambda)$ $J$ $J_{0}$
根据假设(1), 对于 $\lambda\in \mathbb{R} $ $\lambda\neq \tilde{\mu}_{1},~\tilde{\mu}_{2}$
(2.14) $\begin{matrix}r(\lambda):=\frac{b^{\ast}(\lambda)}{a(\lambda)},~~\tilde{r}(\lambda):=\frac{b(\lambda)}{a(\lambda)}.\end{matrix}$
结合散射关系(2.11)和反射系数(2.14), 有
(2.15) $J_{0}(\lambda)=\left(\begin{array}{cc}1+r r^{*} & r^{*} \\ r & 1\end{array}\right)=\left(\begin{array}{cc}1 & r^{*} \\ 0 & 1\end{array}\right)\left(\begin{array}{ll}1 & 0 \\ r & 1\end{array}\right), \lambda \in \mathbb{R}, \lambda \neq \tilde{\mu}_{1}, \tilde{\mu}_{2}$.
考虑到 $n(x, t, \lambda)$ $\Gamma_{1}$ $\Gamma_{2}$
情况(1) $\Gamma_{1}\cap\Gamma_{2}\neq\emptyset$ $\Leftrightarrow$ $\tilde{\mu}_{1}= \tilde{\mu}_{2}$ .
情况(2) $\Gamma_{1}\cap\Gamma_{2}=\emptyset$ $\Leftrightarrow$ $\tilde{\mu}_{1}\neq\tilde{\mu}_{2}$ .
现已存在情况(1)的相关研究[38 ⇓ ⇓ -41 ] , 故在这里重点探讨另一种情况.
引理 2.1 当 $\tilde{\mu}_{1}\neq \tilde{\mu}_{2}$ $J_{0}$
(2.16) $J_{0}=\left\{\begin{array}{l}\left(\begin{array}{cc}1 & 0 \\ \frac{\mathrm{ie}^{-\mathrm{i} \theta_{1}}}{a_{+} a_{-}} & 1\end{array}\right), \lambda \in \Gamma_{1} \cap \mathbb{C}^{+}, \\ \left(\begin{array}{cc}\frac{a_{-}}{a_{+}} & \mathrm{ie}^{\mathrm{i} \theta_{2}} \\ 0 & \frac{a_{+}}{a_{-}}\end{array}\right), \lambda \in \Gamma_{2} \cap \mathbb{C}^{+},\end{array} \quad J_{0}=\left\{\begin{array}{c}\left(\begin{array}{cc}1 & \frac{\mathrm{ie} \mathrm{e}^{\mathrm{i} \theta_{1}}}{a_{+}^{*} a_{-}^{*}} \\ 0 & 1\end{array}\right), \lambda \in \Gamma_{1} \cap \mathbb{C}^{-}, \\ \left(\begin{array}{cc}\frac{a_{+}^{*}}{a_{-}^{*}} & 0 \\ \mathrm{ie}^{-\mathrm{i} \theta_{2}} & \frac{a_{-}^{*}}{a_{+}^{*}}\end{array}\right), \lambda \in \Gamma_{2} \cap \mathbb{C}^{-}.\end{array}\right.\right.$
证 当 $\lambda\in\Gamma_{1}\cup\Gamma_{2}$
对于任意给定的 $(y,t)$ $u$ $u_{0j}$ $\Upsilon_{0j}(x,y)$ $x$ $x = y$ $X$ $\lambda$ $\Upsilon_{0j}(x,y)$ $\lambda\in\Gamma_{1}\cup\Gamma_{2}$
(2.17) $\begin{matrix}&&\Phi_{1\pm}=\Xi_{1}\Phi_{01\pm},~~\Phi_{2}=\Xi_{2}\Phi_{02},~~\lambda\in\Gamma_{1},\\&&\Phi_{2\pm}=\Xi_{2}\Phi_{02\pm},~~\Phi_{1}=\Xi_{1}\Phi_{01},~~\lambda\in\Gamma_{2}.\end{matrix}$
引入散射矩阵 $S_{\pm}(\lambda)$
(2.18) $\begin{matrix}&&\Phi_{2}(x,t,\lambda)=\Phi_{1\pm}(x,t,\lambda)S_{\pm}(\lambda),~~\lambda\in\Gamma_{1},\\&&\Phi_{2\pm}=\Phi_{1}(x,t,\lambda)S_{\pm}(\lambda),~~\lambda\in\Gamma_{2}.\end{matrix}$
接下来分别讨论 $\lambda\in\Gamma_{1}$ $\lambda\in\Gamma_{2}$
对于 $\lambda\in\Gamma_{1}$
令 $x = t = 0$ $S_{\pm}(\lambda)=(M_{1\pm})^{-1}(\lambda)D_{1}(\lambda)$ $M_{1\pm}(\lambda)$ $j$ $1\pm$
(2.19) $\begin{matrix}D_{1}(\lambda):=\Xi_{1}^{-1}(0,0,\lambda)\Phi_{2}(0,0,\lambda).\end{matrix}$
结合(2.7), (2.8)和(2.11)式, 可计算出
(2.20) $S_{-}(\lambda)=\left(\begin{array}{cc}0 & \mathrm{ie}^{\mathrm{i} \theta_{1}} \\ \mathrm{ie}^{-\mathrm{i} \theta_{1}} & 0\end{array}\right) S_{+}(\lambda), \quad \lambda \in \Gamma_{1}$
(2.21) $\begin{equation}S_{21-}={\rm i}{\rm e}^{-{\rm i}\theta_{1}}S_{11+},~~S_{22-}={\rm i}{\rm e}^{-{\rm i}\theta_{1}}S_{12+},~~\lambda\in\Gamma_{1}.\end{equation}$
(2.22) $\left(\frac{\Phi_{1+}^{(1)}}{a_{+}} \Phi_{2}^{(2)}\right)=\left(\frac{\Phi_{1-}^{(1)}}{a_{-}} \Phi_{2}^{(2)}\right)\left(\begin{array}{ll}1 & 0 \\ c_{1} & 1\end{array}\right), \lambda \in \Gamma_{1} \cap \mathbb{C}^{+}$,
其中 $c_{1}\equiv c_{1}(\lambda)$ .
(2.23) \begin{matrix} $\Phi_{1\pm}^{(2)}=S_{22\pm}\Phi_{2}^{(1)}-S_{21\pm}\Phi_{2}^{(2)}.\end{matrix}$
由于 $\det\Phi_{2}=1$ $\det\left(\Phi_{1\pm}^{(1)}~\Phi_{2}^{(2)}\right)=S_{22\pm}$ .
(2.24) $\begin{equation}S_{22\pm}=a_{\pm},~~\lambda\in\Gamma_{1}\cap{\Bbb C}^{+}.\end{equation}$
进一步, 考虑(2.21)和(2.22)式, 计算得到
(2.25) $\begin{matrix}\frac{S_{21-}}{S_{22-}}-\frac{S_{21+}}{S_{22+}}=\frac{{\rm i}{\rm e}^{-{\rm i}\theta_{1}}}{a_{+}a_{-}}=c_{1}.\end{matrix}$
类似地, 对于 $\lambda\in\Gamma_{2}$
其次, 当 $x = t = 0$ $S_{\pm}(\lambda)=D_{2}(\lambda)M_{2\pm}(\lambda)$
(2.26) $\begin{matrix}D_{2}(\lambda):= \Phi_{1}^{-1}(0,0,\lambda)\Xi_{2}(0,0,\lambda).\end{matrix}$
基于上述推导过程, 最终求得 $c_{2}={\rm i}{\rm e}^{{\rm i}\theta_{2}}$ . 证毕.
根据假设(2), 当 $\tilde{\mu}_{1}\neq \tilde{\mu}_{2}$ $B>0$ $u_{0}(x)$
(2.27) $\begin{matrix}u_{0}(x)\sim\left\{\begin{array}{ll} A_{1}{\rm e}^{{\rm i}(\mu_{1}x+\theta_{1})}, & x<-B, \\ A_{2}{\rm e}^{{\rm i}(\mu_{2}x+\theta_{2})}, & x>B.\end{array}\right.\end{matrix}$
此外, 散射系数 $a(\lambda)$ $b(\lambda)$ ${\Bbb C} \setminus (\Gamma_{1}\cup\Gamma_{2})$
对于 $\lambda\in\Gamma_{1}\cup\Gamma_{2}$
(2.28) $\begin{matrix}\left\{\begin{array}{ll} a_{+}=-{\rm i}{\rm e}^{-{\rm i}\theta_{1}}b_{-}, \\ b_{+}=-{\rm i}{\rm e}^{{\rm i}\theta_{1}}a_{-}, \end{array}\right.~\lambda\in\Gamma_{1};~~\left\{\begin{array}{ll} a_{+}=-{\rm i}{\rm e}^{-{\rm i}\theta_{2}}b_{-}^{\ast}, \\ b_{+}=-{\rm i}{\rm e}^{{\rm i}\theta_{2}}a_{-}^{\ast}, \end{array}\right.~\lambda\in\Gamma_{2}.\end{matrix}$
同样地, 由 $c_{2}$
(2.29) $\begin{matrix}r_{+}(\lambda)-r_{-}(\lambda)=\frac{{\rm i}{\rm e}^{-{\rm i}\theta_{1}}}{a_{+}a_{-}},~\lambda\in\Gamma_{1};~~\tilde{r}_{+}(\lambda)-\tilde{r}_{-}(\lambda)=\frac{{\rm i}{\rm e}^{{\rm i}\theta_{2}}}{a_{+}a_{-}},~\lambda\in \Gamma_{2}.\end{matrix}$
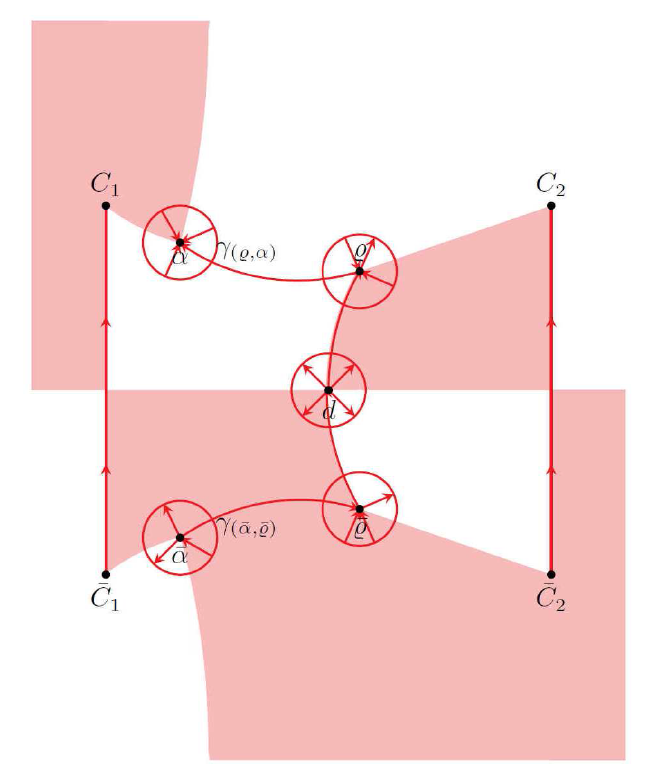
其中 $D_{1}(\lambda)$ $D_{2}(\lambda)$ $\lambda\in{\Bbb C}\setminus\Gamma_{1}\cup\Gamma_{2}$ $D_{j}(\lambda)$ $\Xi_{j}$ $\theta_{1}$ $\theta_{2}$ $C_{2}$ $C_{1}$ $D_{2}$ $D_{1}$ $C_{2}$ $C_{1}$
对于 $C_{2}$ $\lambda$
而对于 $C_{1}$
命题 2.2 假设 $(1 + |x|)(u_{0}(x)-u_{01}(x)) \in L^{1}((-\infty, 0])$ . 给定 $x\in\mathbb{R} $ $\epsilon \in(0, {\rm Im} C_{1})$ $B_{\epsilon}(C_{1})$ $B_{\epsilon}(\bar{C}_{1})$ $C_{1}$ $\bar{C}_{1}$ $\epsilon$ $\Phi_{1}$
取 $x = t = 0$ $S(\lambda)=M_{1}^{-1}(\lambda)M_{2}(\lambda)={\rm e}^{\frac{{\rm i}\theta_{1}}{2}\hat{\sigma}_{3}}\zeta_{1}^{-1}(\lambda){\rm e}^{\frac{{\rm i}\theta_{2}}{2}\hat{\sigma}_{3}}\zeta_{2}(\lambda)$ .
其中, $\nu_{j}\equiv \nu_{j}(\lambda)$ $j = 1, 2$
当 $\lambda = C_{1}$ $J_{0}$ $\Gamma_{1}$ $\Gamma_{2}$ $|\lambda-C_{j}|^{-\frac{1}{4}}$ $|\lambda-\bar{C}_{j}|^{-\frac{1}{4}}$ . 对于任意 $\lambda\in {\Bbb C}^{+}\cup\mathbb{R} \setminus\{C_{2}\}$ $a(\lambda)\neq 0$
接下来给出基本的 Riemann-Hilbert 问题的定义.
定义 2.1 给定 $r(\lambda)$ $\lambda\in \mathbb{R} $ $a_{\pm}(\lambda)$ $\lambda\in\Gamma_{1}\cup\Gamma_{2}\cap{\Bbb C}^{+}$ . 矩阵函数 $n(x, t, \lambda)$ $\lambda\in{\Bbb C}\setminus\Gamma$
(1) 跳跃条件(2.1), 其中跳跃矩阵 $J_{0}$
(2) 正则化条件: 当 $n(x, t, \lambda)\rightarrow {\Bbb I}$ $\lambda \rightarrow\infty$
(3) 在 $\Gamma_{1}$ $\Gamma_{2}$ $|\lambda-C_{j}|^{-\frac{1}{4}}$ $|\lambda-\bar{C}_{j}|^{-\frac{1}{4}}$ .
若 $n(x, t, \lambda)$ $u(x, t)$
(2.30) $\begin{matrix}u(x, t){\rm e}^{2{\rm i}\beta\int_{x}^{+\infty}(|u(y,t)|^{2}-A^{2}){\rm d}y}=2{\rm i}\lim_{\lambda \rightarrow\infty}\lambda \left(n(x, t, \lambda)\right)_{12}.\end{matrix}$
3 稀疏情况: $\tilde{\mu}_{2}<\tilde{\mu}_{1}$
非线性可积系统柯西问题的解可以通过构造并求解相关 Riemann-Hilbert 问题来表示, 这使得非线性速降法能够更好地分析解的长时间渐进性. 据我们所知, 该方法最初是针对初边值条件为零的情况[21 ] 提出的. 为了解决非零初边值的问题, 出现了所谓的 $g$ [22 ] , 它与跳跃矩阵的某些项随着 $t$
利用函数 $g(\xi, \lambda)$
(3.1) $\begin{matrix}\phi(\xi,\lambda):=\xi \lambda+\lambda^{2},~~\xi:=x/t,\end{matrix}$
从而实现在特定区域上的跳跃变形. 通过对跳跃矩阵进行适当的三角因式分解, 并对基本的Riemann-Hilbert 问题进行相应的变形, 使最初包含指数增长项的跳跃矩阵转变成具有特定结构的分段常数矩阵, 且这些矩阵仅与 $x$ $t$
考虑极限 Riemann-Hilbert 问题的结构, 利用与该问题相关的黎曼函数和黎曼曲面上的 Abel 积分计算得到该问题的显式解. 根据参数 $\xi$ $A_{j}$ $\beta$ $\mu_{j}$ $(j=1,2)$ $g$ $g$ $g = g^{\ast}$
(3.2) $\begin{matrix}\frac{\partial}{\partial\lambda}g(\xi,\lambda)=\frac{\partial}{\partial \lambda}\phi(\xi,\lambda)+O\left(\lambda^{-2}\right)=2\lambda+\xi+O\left(\lambda^{-2}\right),~~\lambda\rightarrow\infty.\end{matrix}$
由此可推断出水平集 ${\rm Im} g(\xi,\lambda)$ ${\rm Re} \lambda =-\frac{\xi}{2}$ ${\rm Im} g=0$ ${\rm Im} g$
图3.1
图3.1
当 $\xi\gg0\mbox{ 时}$ ${\rm Im}\phi<0$ ${\rm Im}\phi>0$
基于 $\xi$ $\Gamma_{1}$ $\Gamma_{2}$ $g$
(3.3) $\begin{matrix}g_{j}(\xi,\lambda):=\left[\left(\lambda-\frac{\mu_{j}}{2}+\beta A_{j}^{2}\right)+\xi\right]\sqrt{(\lambda+\frac{\mu_{j}}{2}-\beta A_{j}^{2})^{2}+A_{j}^{2}},\end{matrix}$
其中, 当 $\xi\ll 0$ $j = 1$ $\xi\ll 0$ $j = 1$ .
因此, 除了实轴外, 水平集 ${\rm Im} g=0$ ${\rm Re} \lambda =-\frac{\xi}{2}$ $C_{j}$ $\bar{C}_{j}$ $\Gamma_{j}$ .
注3.1 接下来, 考虑包含相应 $g$ $\lambda$ $C_{j}$ $\bar{C}_{j}$ $g_{j}$ $(C_{j},\bar{C}_{j})$ .
定义 $B_{1}=\frac{\mu_{1}}{2}-\beta A_{1}^{2}-\sqrt{2}A_{1}$ $B_{2}=\frac{\mu_{2}}{2}-\beta A_{2}^{2}+\sqrt{2}A_{2}$ . 上半复平面可被划分为五个区域, 如图3 .2所示.
图3.2
当 $\xi<2B_{1}$ $\xi>2B_{2}$
假设 $\xi\gg 0$ $g \equiv g_{2}(\xi, \lambda)$ $g$ $\lambda$
(3.4) $\begin{matrix}\frac{\partial}{\partial \lambda}g(\xi,\lambda)=2\frac{(\lambda-d_{1}(\xi))(\lambda-d_{2}(\xi))}{\sqrt{(\lambda-C_{2})(\lambda-\bar{C}_{2})}}.\end{matrix}$
由 ${\rm Im}g_{2}(\xi,\lambda)=0$
此外 $\xi>-2d_{1}>-2d_{2}>\mu_{2}-2\beta A_{2}^{2}$ .
图3.3
图3.3
$\xi>\xi_{m}$ $\xi=\xi_{m}$
(3.5) $\begin{matrix}n^{(1)}(x,t,\lambda):={\rm e}^{-{\rm i}tg_{j}^{(0)}(\xi)\sigma_{3}}n(x,t,\lambda){\rm e}^{-{\rm i}t(g_{j}(\xi,\lambda)-\phi(\xi,\lambda))\sigma_{3}},~~j=1, 2,\end{matrix}$
(3.6) $\begin{matrix}&&g_{j}^{(0)}(\xi):=\omega_{j}+ \frac{\xi\mu_{j}}{2}=A_{j}^{2}-\frac{\mu_{j}^{2}}{2}+2\beta^{2}A_{j}^{4}+\frac{\xi\mu_{j}}{2},\\&&g_{j}(\xi,\lambda)=\lambda^{2}+\xi \lambda+g_{j}^{(0)}(\xi)+O\left(\lambda^{-1}\right),~~\lambda\rightarrow\infty.\end{matrix}$
对于 $\lambda\in\Gamma$ $n_{+}^{(1)}(x,t,\lambda)=n_{-}^{(1)}(x,t,\lambda)J^{(1)}(x,t,\lambda)$ .
更具体地, 当 $\lambda\in\Gamma_{1}$ $t \rightarrow\infty$ $J^{(1)}(x,t,\lambda)$
当 $\lambda\in\Gamma_{2}\cap{\Bbb C^{+}}$
(3.7) $\begin{matrix}J^{(1)}(x,t,\lambda)&=&\left( \begin{array}{cc} \frac{a_{-}(\lambda)}{a_{+}(\lambda)}{\rm e}^{{\rm i}t(g_{2+}(\xi,\lambda)-g_{2-}(\xi,\lambda))} & {\rm i}{\rm e}^{{\rm i}\theta_{2}} \\ 0 & \frac{a_{+}(\lambda)}{a_{-}(\lambda)}{\rm e}^{-{\rm i}t(g_{2+}(\xi,\lambda) -g_{2-}(\xi,\lambda))} \\ \end{array} \right)\\&=&\left( \begin{array}{cc} 1 & 0 \\ -r_{-}(\lambda){\rm e}^{2{\rm i}tg_{2-}(\xi,\lambda)} & 1 \\ \end{array} \right)\left( \begin{array}{cc} 0 & {\rm i}{\rm e}^{{\rm i}\theta_{2}} \\ {\rm i}{\rm e}^{-{\rm i}\theta_{2}} & 0 \\ \end{array} \right)\left( \begin{array}{cc} 1 & 0 \\ r_{+}(\lambda){\rm e}^{2{\rm i}tg_{2+}(\xi,\lambda)} & 1 \\ \end{array} \right).\end{matrix}$
类似地, 当 $\lambda\in\Gamma_{2}\cap{\Bbb C^{-}}$
根据文献[27 ,28 ], 可得两个修正的 Riemann-Hilbert 问题的解 $n^{mod_{-j}}$ $j=1,2$ .
进一步地, 聚焦 KE 方程(1.2)在平面波区域的渐进解 $u(x,t)$
(3.8) $\begin{matrix}u(x, t)&=&{\rm e}^{-2{\rm i}\beta\int_{x}^{+\infty}\left(|u(y,t)|^{2}-A_{j}^{2}\right){\rm d}y}A_{j}{\rm e}^{{\rm i}[\mu_{j}x+(A_{j}^{2}-\frac{\mu_{j}^{2}}{2}+2\beta^{2}A_{j}^{4})t+\phi_{j}(\xi)]}\\&&+O\big(t^{-\frac{1}{2}}\big),~~(-1)^{j}\xi \gg 0,~~j=1, 2,\end{matrix}$
其中 $\phi_{1}(-\infty)=\theta_{1}$ $\phi_{2}(+\infty)=\theta_{2}$ .
当 $2B_{1}<\xi<-2\tilde{\mu}_{1}$ $-2\tilde{\mu}_{2}<\xi<2B_{2}$ $\xi\in(-2\tilde{\mu}_{2},2B_{2})$
当 $\xi$ $2B_{2}$ $g$ $\frac{\partial g}{\partial \lambda}$
(3.9) $\begin{matrix}\frac{\partial}{\partial \lambda}g(\xi,\lambda)=2\frac{(\lambda-d(\xi))(\lambda-\varrho(\xi))(\lambda-\bar{\varrho}(\xi))}{\sqrt{(\lambda-C_{2})(\lambda-\bar{C}_{2})(\lambda-\varrho(\xi))(\lambda-\bar{\varrho}(\xi))}}.\end{matrix}$
此外参数 $d(\xi)$ $\varrho(\xi)$
(1) 当 $\lambda =\infty$
(2) 正则性 $\int_{C_{2}}^{\bar{C}_{2}}{\rm d}g=0$ .
参考 Riemann-Hilbert 问题在文献[25 ]中进一步变形的过程.
当 $\lambda\in \Gamma_{j},~j=1,2$
(3.10) $\begin{matrix}\left\{\begin{array}{ll} n^{mod}\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus(\Gamma_{1}\cup\Gamma_{2})),\\ n_{+}^{mod}(\lambda)={\rm i}n_{-}^{mod}(\lambda)\left(\begin{array}{cc} 0 & {\rm e}^{{\rm i}(P_{j}x+G_{j}t)}{\rm e}^{\theta_{j}} \\ {\rm e}^{-{\rm i}(P_{j}x+G_{j})}{\rm e}^{\theta_{j}} & 0 \\ \end{array} \right). \end{array}\right.\end{matrix}$
由(2.5)式, 可得 $\nu_{2}-\frac{1}{\nu_{2}}$ $\lambda_{2}$ .
设$\Lambda_{1}(\lambda_{2})$ $\Lambda_{2}(\lambda_{2})$ $\lambda_{2}$
(3.11) $\begin{matrix}b_{2}=-\int_{\bar{C}_2}^{\Lambda_{2}(\lambda_{2})}\frac{w_{0}}{U_{2}(\lambda)}{\rm d}\lambda.\end{matrix}$
其中实常数 $w_{0}=\big(\oint_{\Gamma_{2}}\frac{{\rm d}\lambda}{U_{2}(\lambda)}\big)^{-1}$ .
因此, 聚焦 KE 方程(1.2)在该区域渐进解可用亏格为 1 黎曼曲面
(3.12) $\begin{matrix}f_{2}^{2} =(\lambda-C_{2})(\lambda-\bar{C}_{2})(\lambda-{\varrho}(\xi))(\lambda-\bar{\varrho}(\xi))\end{matrix}$
其中关于 $\tau\equiv\tau(\xi)$
当 $-2\tilde{\mu}_{1}<\xi<-2\tilde{\mu}_{2}$
首先定义一个 $g$ $\tilde{\mu}_{2}$ $g(\xi, \lambda) =\phi(\xi, \lambda)$ $u(x, t) = O\big(t^{-\frac{1}{2}}\big)$ . 为了得到在临界点 $\lambda = -\frac{\xi}{2} \in\mathbb{R} $ $u(x,t)$
图3.4
图3.4
慢衰减情况下, ${\rm Im}\phi<0$ ${\rm Im}\phi>0$
根据文献[21 ], 通过对基本的 Riemann-Hilbert 问题变形可得到一个新的可解的 Riemann-Hilbert 问题.
定义 $\Gamma_{p} :=(-\infty, -\frac{\xi}{2})\cup \Gamma_{2}$ . 设函数 $p(\lambda)\equiv p(\xi, \lambda)$ $\Gamma_{p}$ $p_{+}(\lambda) = p_{-}(\lambda)J_{p}(\lambda)$
(3.14) $\begin{matrix}J_{p}=\left\{\begin{array}{ll} 1+|r|^{2},~~&\lambda\in (-\infty, -\frac{\xi}{2}), \\[2mm] \frac{a_{-}}{a_{+}},~~~~&\lambda\in \Gamma_{2}\cap{\Bbb C}^{+}, \\[3mm] \frac{a_{+}^{\ast}}{a_{-}^{\ast}},~&\lambda\in \Gamma_{2}\cap{\Bbb C}^{-}, \end{array} \right.\end{matrix}$
此外, 当 $\lambda\rightarrow\infty$ $p(\lambda)\rightarrow 1$ .
根据柯西积分公式, 可得$p(\lambda)=\exp\left\{\frac{1}{2\pi{\rm i}}\int_{\Gamma_{p}}\frac{\log J_{p}(k)}{k-\lambda}{\rm d}k\right\}=p_{0}p_{1}p_{2}$
设 $\lambda_{0}=-\frac{\xi}{2}$ $\lambda\rightarrow \lambda_{0}$ $p_{0}(\lambda)=\left(\lambda+\frac{\xi}{2}\right)^{{\rm i}\nu(-\frac{\xi}{2})}{\rm e}^{\chi(\lambda)}$
进一步地,$p_{1}(\lambda_{0})p_{2}(\lambda_{0})=\exp\bigg \{\frac{{\rm i}}{\pi}{\rm Im}\int_{0}^{\infty}\frac{\log \frac{a_{-}({\rm i}\tau)}{a_{+}({\rm i}\tau)}}{{\rm i}\tau+\frac{\xi}{2}}{\rm d}\tau\bigg\}$ .
基于以上分析, 对基本的 Riemann-Hilbert 问题进行第一次变形.
当 $\lambda\in {\Bbb C}\setminus\Gamma$
其满足 $n_{+}^{(1)}(x,t,\lambda):=n_{-}^{(1)}(x,t,\lambda){\rm e}^{-{\rm i}t\phi(\xi,\lambda)\hat{\sigma}_{3}}J_{0}^{(1)}(\lambda)$ $J_{0}^{(1)} = p_{-}^{\sigma_{3}}J_{0}p_{+}^{-\sigma_{3}}$ .
当 $\lambda\in \Gamma_{1}\cup\Gamma_{2}$ $J_{0}^{(1)}$
当 $\lambda\in\mathbb{R} $
(3.15) $J_{0}^{(1)}=\left\{\begin{array}{ll}\left(\begin{array}{cc}1 & r^{*} p^{2} \\ 0 & 1\end{array}\right)\left(\begin{array}{cc}1 & 0 \\ r p^{-2} & 1\end{array}\right), & \lambda \in\left(-\frac{\xi}{2},+\infty\right), \\ \left(\begin{array}{cc}1 & 0 \\ \frac{r}{p_{+} p_{-}} & 1\end{array}\right)\left(\begin{array}{cc}1 & r^{*} p_{+} p_{-} \\ 0 & 1\end{array}\right), & \lambda \in\left(-\infty,-\frac{\xi}{2}\right), \\ \left(\begin{array}{cc}1 & 0 \\ \frac{\mathrm{ie}^{-\mathrm{i} \theta_{1}}}{a_{+} a_{-}} & 1\end{array}\right), & \lambda \in \Gamma_{1} \cap \mathbb{C}^{+}, \\ \left(\begin{array}{ll}1 & \mathrm{ie}^{\mathrm{i} \theta_{2}} p_{+} p_{-} \\ 0 & 1\end{array}\right), & \lambda \in \Gamma_{2} \cap \mathbb{C}^{+}, \\ \sigma_{2} J_{0}^{(1) *} \sigma_{2}, & \lambda \in\left(\Gamma_{1} \cap \Gamma_{2}\right) \cap \mathbb{C}^{-}.\end{array}\right.$
第二次变形旨在减少在以 $-\frac{\xi}{2}$ $\Sigma_{cr}=\bigcup\limits_{j=1}^{4}L_{j}$
(3.16) $\begin{matrix}n^{(2)}(x,t,\lambda):=n^{(1)}(x,t,\lambda){\rm e}^{-{\rm i}t\phi(\xi,\lambda)\hat{\sigma}_{3}}G(\lambda),\end{matrix}$
(3.17) $G \equiv G(\lambda)=\left\{\begin{array}{ll}\left(\begin{array}{cc}1 & 0 \\ -r p^{-2} & 1\end{array}\right), & \lambda \in P_{1}, \\ \mathbb{I}, & \lambda \in P_{2}, \\ \left(\begin{array}{cc}1 & -\tilde{r} a^{2} p^{2} \\ 0 & 1\end{array}\right), & \lambda \in P_{3}, \\ \left(\begin{array}{cc}1 & 0 \\ \tilde{r}^{*} a^{* 2} p^{-2} & 1\end{array}\right), & \lambda \in P_{4}, \\ \mathbb{I}, & \lambda \in P_{5}, \\ \left(\begin{array}{cc}1 & r^{*} p^{2} \\ 0 & 1\end{array}\right), & \lambda \in P_{6},\end{array}\right.$
反射系数 $r$ $\tilde{r}$
(3.18) $\begin{matrix}n_{+}^{(2)}(x,t,\lambda):=n_{-}^{(2)}(x,t,\lambda){\rm e}^{-{\rm i}t\phi(\xi,\lambda)\hat{\sigma}_{3}}J_{0}^{(2)}(\lambda),~~\lambda\in\Gamma\cup \Sigma_{cr},\end{matrix}$
跳跃矩阵为 $J_{0}^{(2)}=G_{-}^{-1}J_{0}^{(1)}G_{+}$
$\bullet$ $\lambda\in\mathbb{R} $ $J_{0}^{(2)}= {\Bbb I}$
$\bullet$ $\lambda \in \Sigma_{cr}$
通过将 $n^{(2)}$ [21 ] 进行对比, 发现唯一差异是近似中的一个只与 $\xi$ $p(\lambda)$ .
当 $\lambda \rightarrow -\frac{\xi}{2}$ $p(\lambda)\sim\left(\lambda +\frac{\xi}{2}\right)^{{\rm i}\nu(-\frac{\xi}{2})}{\rm e}^{\tilde{\chi}(-\frac{\xi}{2})}$
最后, 聚焦 KE 方程(1.2)在慢衰减区域的渐进解被定义为(1.8)式, 其中参数 $b_{j}$ $j=0, 1, 2, 3$
(3.19) $\begin{matrix}&&b_{0}=\sqrt{\frac{\log(1+|r(-\frac{\xi}{2})|^{2})}{4\pi}},~~b_{1}=\frac{\xi^{2}}{2},~~b_{2}=-\nu(-\frac{\xi}{2}),\\&&b_{3}=-3\log2\nu(-\frac{\xi}{2})+\arg\Gamma({\rm i}\nu(-\frac{\xi}{2}))-\arg r(-\frac{\xi}{2})-2{\rm i}\tilde{\chi}(-\frac{\xi}{2})+\frac{\pi}{4}.\end{matrix}$
4 激波情况: $\tilde{\mu}_{2}>\tilde{\mu}_{1}$
首先定义 $\hat{n}(x,t,\lambda):=n(x,t,\lambda)\nu_{1}^{\sigma_{3}}(\lambda),$ $\nu_{1}(\lambda)$ $\hat{a}:=a\nu_{1}$ $\hat{b}:=b\nu_{1}$ $\hat{r}:=\frac{\hat{b}^{\ast}}{\hat{a}}=\frac{b^{\ast}\nu_{1}^{\ast}}{a\nu_{1}}=r\nu_{1}^{-2}$ . 然后, 计算得到 $\hat{a}\hat{a}^{\ast}=aa^{\ast}$ $\hat{b}\hat{b}^{\ast}=bb^{\ast}$ $|\hat{r}|^{2}=\hat{r}\hat{r}^{\ast}=rr^{\ast}=|r|^{2}$ .
函数 $\hat{n}(x,t,\lambda)$
(4.1) $\begin{matrix}\hat{J}_{0}=\nu_{1-}^{\sigma_{3}}J_{0}\nu_{1+}^{-\sigma_{3}}\end{matrix}$
表示, 其中 $J_{0}$ $\hat{n}(x,t,\lambda)$ $\hat{J}$
那么柯西问题(1.2)-(1.3)的解 $u(x,t)$
(4.2) $\begin{matrix}u(x, t){\rm e}^{2{\rm i}\beta\int_{x}^{+\infty}(|u(y,t)|^{2}-A^{2}){\rm d}y}=2{\rm i}\lim_{\lambda \rightarrow\infty}\lambda\left(\hat{n}(x, t, \lambda)\right)_{12}.\end{matrix}$
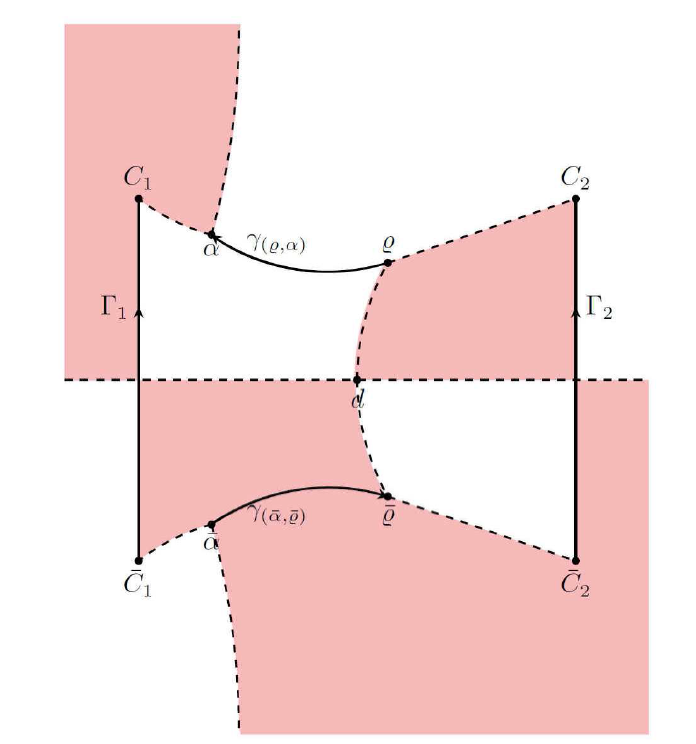
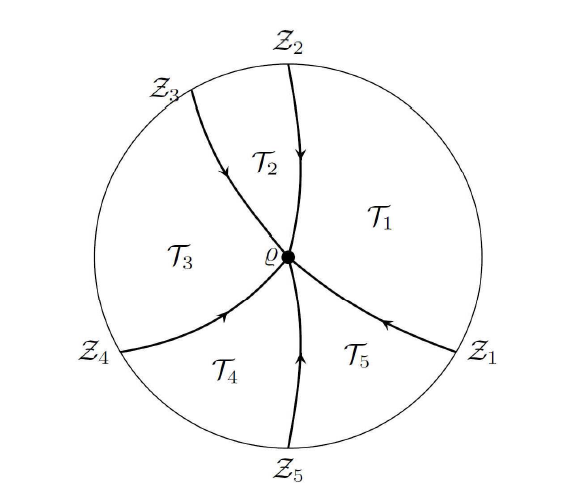
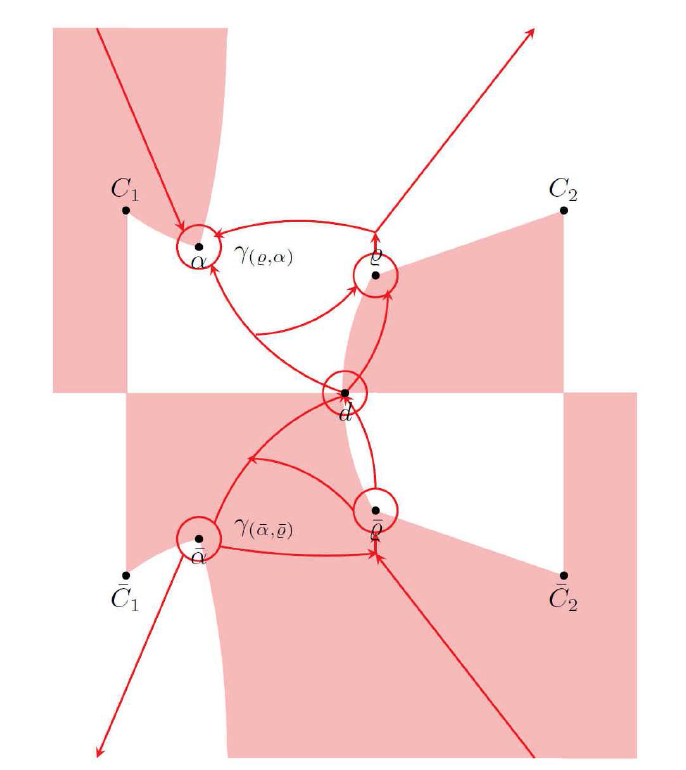
针对激波情况, 需要分析解在亏格为 3的 黎曼曲面上的渐进性. 在该区域, $g$ $d\equiv d(\xi)$ $\{\alpha,\bar{\alpha}\}$ $\{\varrho,\bar{\varrho}\}$ $\alpha\equiv \alpha(\xi)$ $\varrho\equiv \varrho(\xi)$ ${\Bbb C}^{+}\setminus(\Gamma_{1}\cup\Gamma_{2})$ . 接下来需要在每个跳跃曲线上定义合适的 $g$
在图4 .1 中, 当 $A_{1} = A_{2} = 3/2$ $\xi = 1$ ${\rm Im} g = 0$ . 从 $\varrho$ $\alpha$ $\bar{\alpha}$ $\bar{\varrho}$ $\bar{\varrho}$ $\varrho$ $\gamma_{(\varrho,\alpha)}$ $\gamma_{(\bar{\alpha},\bar{\varrho})}$ $\gamma_{(\bar{\varrho},\varrho)}$ . 超椭圆曲面 $N\equiv N_{\alpha\varrho}$ $P := (\omega,\lambda)\in {\Bbb C}^{2}$
图4.1
图4.1
跳跃曲线(黑色实线), ${\rm Im} g <0$ ${\rm Im} g >0$
若分支曲线集 ${\cal C}:=\Gamma_{1}\cup\Gamma_{2}\cup\gamma_{(\varrho,\alpha)}\cup\gamma_{(\bar{\alpha},\bar{\varrho})}$ $N$ $\lambda\in \overline{{\Bbb C}}\setminus {\cal C}$ $N$ $\lambda^{+}$ $\lambda^{-}$ $\lambda\rightarrow\infty$ $\omega = \lambda^{4} + O(\lambda^{3})$ $\omega = -\lambda^{4} + O(\lambda^{3})$ . 设$\varpi=(\varpi_{1}, \varpi_{2}, \varpi_{3})$ ${\cal H}^{1}(N)$ $\{a_{j},b_{j}\}_{1}^{3}$ $\int_{a_{i}}\varpi_{j}{\rm d}\lambda=\delta_{ij}$ $\varpi_{j}=\sum\limits_{l=1}^{3}A_{jl}\hat{\varpi}_{l}$ $\hat{\varpi}_{l}:=\frac{\lambda^{l-1}}{\omega}$ $\left(A^{-1}\right)_{jl}=\int_{a_{j}}\hat{\varpi}_{l}{\rm d}\lambda$ $\tau_{jl}:=\int_{b_{j}}\varpi_{l}{\rm d}\lambda$ $3\times3$
对于 $z\in {\Bbb C}^{3}$ $\tau$ $\Theta(z):=\sum\limits_{M\in{\Bbb Z}^{3}}{\rm e}^{2\pi{\rm i}(\frac{1}{2}M^{T}\tau M+M^{T}z)}$
定义一个 Abel-型映射 $\varphi: N \rightarrow{\Bbb C}^{3}$ . 对于 $D\in N$ $\varphi(D)=\int_{\bar{C}_{2}}^{D}\varpi {\rm d}\lambda$ .
当 $\lambda\in {\Bbb C}\setminus{\cal C}$ $g$ $\lambda$
(4.3) $\begin{matrix}\frac{\partial}{\partial \lambda}g(\xi,\lambda)=2\frac{(\lambda-d(\xi))(\lambda-\alpha(\xi))(\lambda-\bar{\alpha}(\xi))(\lambda-\varrho(\xi))(\lambda-\bar{\varrho}(\xi))}{\omega(\lambda)},\end{matrix}$
其中, $d\equiv d(\xi)$
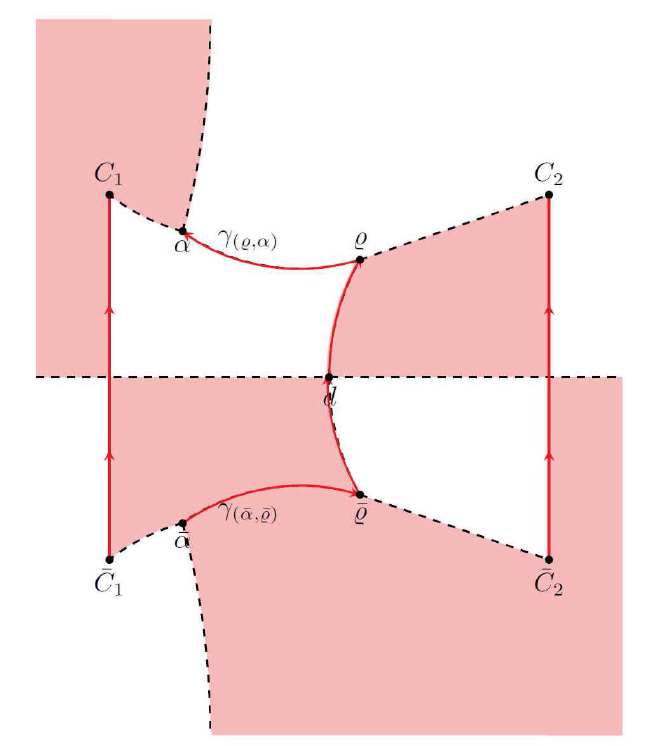
图4.2
图4.2
跳跃曲线(红色实线), ${\rm Im} g <0$ ${\rm Im} g >0$
定义 $\Gamma^{mod} := {\cal C}\cup\gamma_{(\bar{\varrho},\varrho)} = \Gamma_{1}\cup\Gamma_{2}\cup\gamma_{(\varrho,\alpha)}\cup \gamma_{(\bar{\alpha},\bar{\varrho})}\cup\gamma_{(\bar{\varrho},\varrho)}$ .
对于 $\lambda\in{\Bbb C}\setminus\Gamma^{mod}$ $g$
(4.4) $\begin{matrix}g(\lambda)\equiv g(\xi, \lambda):=\int_{\bar{C}_{2}}^{\lambda}{\rm d}g,\end{matrix}$
$\bullet$ $\lambda\in\overline{{\Bbb C}}\setminus\Gamma^{mod}$ $g(\lambda)-\lambda^{2}-\xi \lambda$ $\Gamma^{mod}$
$\bullet$ $g=g^{\ast}$
$\bullet$ $\lambda\in\gamma_{(\bar{\varrho},\varrho)}$ $g_{+}(\lambda)-g_{-}(\lambda)= 2H_{1}$
其中, $H_{j}\equiv H_{j}(\xi)$ $j=1, 2, 3$
在某些情况下, 可以通过改变跳跃曲线定义新的 Riemann-Hilbert 问题.
图4.3
图4.3
跳跃曲线 $\Sigma$ $\hat{\Sigma}= \Sigma\cup\gamma$
根据图4 .3, 引入矩阵 Riemann-Hilbert 问题
(4.5) $\begin{equation}\left\{\begin{array}{ll} n\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus\Sigma), \\ n_{+}=n_{-}v, ~\lambda\in\Sigma, \end{array}\right.\end{equation}$
其中, $v : \Sigma\rightarrow GL(2,{\Bbb C})$ $\Sigma$
引理 4.1 设 $q$ $q^{-1}\in E^{\infty}({\Bbb C}\setminus\hat{\Sigma})$ $2\times2$ $n$ $\lambda\in{\Bbb C}\setminus\hat{\Sigma}$ $\hat{n}(\lambda):=n(\lambda)q(\lambda)$
(4.6) $\begin{equation}\left\{\begin{array}{ll} \hat{n}\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus\hat{\Sigma}), \\ \hat{n}_{+}=\hat{n}_{-}\hat{v}, ~\lambda\in \hat{\Sigma}, \end{array}\right.\end{equation}$
(4.7) $\begin{equation}\hat{v}=\left\{\begin{array}{ll} q_{-}^{-1}vq_{+},~~&\lambda\in\Sigma,\\ q_{-}^{-1}q_{+},~~~&\lambda\in\gamma. \end{array}\right.\end{equation}$
当 $q(\infty) \neq{\Bbb I}$
引理 4.2 设 $q$ $q^{-1}\in E^{\infty}({\Bbb C}\setminus\hat{\Sigma})$ $2\times2$ $\lambda =\infty$ $n$ $\lambda\in{\Bbb C}\setminus\hat{\Sigma}$ $\hat{n}(\lambda):=q(\infty)^{-1}n(\lambda)q(\lambda)$ $\hat{v}$
为得到 Riemann-Hilbert 问题(4.6)的解 $\hat{n}$ $\hat{n}^{(j)}(x, t, \lambda)$ $j = 1, 2, \cdots, 5$
(4.8) $\begin{matrix}\left\{\begin{array}{ll} \hat{n}^{(j)}(x,t,\cdot)\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus\Gamma^{(j)}),~~~~~~~~~~~~~~~~~~~~~ \\ \hat{n}^{(j)}_{+}(x, t, \lambda)=\hat{n}^{(j)}_{-}(x, t, \lambda)\hat{v}^{(j)}(x, t,\lambda), ~\lambda\in \Gamma^{(j)}, \end{array}\right.\end{matrix}$
经过五次变形后, 可得到跳跃矩阵 $\hat{v}^{(5)}$ . 当 $t \rightarrow\infty$
类似于(2.2)和(2.3)式, 对于五次跳跃曲线变形, 跳跃矩阵均满足
(4.9) $\begin{matrix}\hat{v}^{(j)}(x, t, \lambda)=\left\{\begin{array}{ll} \sigma_{2}\overline{\hat{v}^{(j)}(x, t, \bar{\lambda})}\sigma_{2}, & \lambda\in \Gamma^{(j)}\setminus\mathbb{R}, \\ \sigma_{2}\overline{\hat{v}^{(j)}(x, t, \bar{\lambda})}^{-1}\sigma_{2}, & \lambda\in \Gamma^{(j)}\cap\mathbb{R}, \end{array}\right.~~j=1, 2, \cdots, 5.\end{matrix}$
(4.10) $\begin{matrix}\hat{n}^{(j)}=\sigma_{2}\overline{\hat{n}^{(j)}(x, t, \bar{\lambda})}\sigma_{2},~~\lambda\in {\Bbb C}\setminus\Gamma^{(j)},~~j=1, 2, \cdots, 5.\end{matrix}$
通过将(3.5)和(3.6)式中的 $n^{(1)}$ $\hat{n}^{(1)}$ $\Gamma^{(1)} := \mathbb{R} \cup\Gamma_{1}\cup\Gamma_{2}\cup\gamma_{(\varrho,\alpha)}\cup \gamma_{(\bar{\alpha},\bar{\varrho})}\cup\gamma_{(\bar{\varrho},\varrho)},$ $\hat{v}^{(1)}(x,t,\lambda):={\rm e}^{-{\rm i}tg_{-}(\lambda)\sigma_{3}}\hat{J}_{0}(\lambda) {\rm e}^{{\rm i}tg_{+}(\lambda)\sigma_{3}}.$ $\lambda\in\mathbb{R} \cup\Gamma_{1}\cup\Gamma_{2}$ $\hat{J}_{0}(\lambda)$ $\lambda\in\gamma_{(\varrho,\alpha)}\cup \gamma_{(\bar{\alpha},\bar{\varrho})}\cup\gamma_{(\bar{\varrho},\varrho)}$ $\hat{J}_{0}(\lambda)$
通过对跳跃矩阵 $\hat{v}^{(1)}$ $\lambda\in(-\infty,d)$
(4.11) $\begin{matrix}\hat{n}^{(2)}(x,t,\lambda):=\hat{n}^{(1)}(x,t,\lambda)\delta(\lambda)^{-\sigma_{3}},\end{matrix}$
其中, 对于 $\lambda\in{\Bbb C}\setminus(-\infty,d]$
$\bullet$ $\delta(\lambda)$ $\delta(\lambda)^{-1}$ $(-\infty,-1)\cup(-1,d)$
$\bullet$ $\delta=(\delta^{\ast})^{-1}$
$\bullet$ $\lambda\in(-\infty, -1)\cup(-1, d)$ $\delta_{+}=\delta_{-}(1+|r|^{2})$
$\bullet$ $\lambda\rightarrow\infty$ $\delta(\lambda)=1+O\left(\lambda^{-1}\right)$ $\arg \lambda\in[2\pi]$
由上述条件可知 $\delta(\xi,\cdot)^{\sigma_{3}}\in{\Bbb I}+(\dot{E}^{2}\cap E^{\infty})\left({\Bbb C}\setminus(\infty,d]\right)$ . 跳跃矩阵有以下形式
在集合 $\{U_{j}\}_{1}^{6}$ $\hat{n}^{(3)}(x,t,\lambda)$
(4.12) $\begin{equation}\hat{n}^{(3)}(x,t,\lambda):=\hat{n}^{(2)}(x,t,\lambda)\times \hat{J}_{j}^{(3)},~~j=1,2,\cdots,6,\end{equation}$
结合(4.8), (4.11)和(4.12)式, 可计算出在 $\Gamma^{(3)}$
本次变形的目的是实现在 $\gamma_{(\varrho, \alpha)}\cup\gamma_{(\bar{\alpha},\bar{\varrho})}$ $\gamma_{(\bar{\varrho}, \varrho)}$ $\lambda\in\{V_{j}\}_{1}^{4}$ $n^{(4)}$
由(4.10)式可知 $\hat{n}^{(4)}$
当 $\lambda\in{\Bbb C}^{+}\setminus\{V_{j}\}_{1}^{4}$ $\hat{J}_{j}^{(4)}={\Bbb I}$ .
根据(4.8), (4.11)和(4.12)式, 函数 $\hat{n}^{(4)}$ $\Gamma^{(4)}$
本次变形旨在实现在四条分支曲线以及 $\gamma_{(\bar{\varrho}, \varrho)}$
这里函数 $h(\lambda)\equiv h(\xi,\lambda)$ $ \overline{{\Bbb C}}\setminus\Gamma^{mod}$ $h=h^{\ast}$ . ${\rm e}^{{\rm i}h(\lambda)\sigma_{3}}\in E^{\infty}\left(\overline{{\Bbb C}}\setminus \Gamma^{mod}\right)$ .
(4.13) $\begin{equation}\hat{v}^{(5)}={\rm e}^{-{\rm i}h_{-}\sigma_{3}}\hat{v}^{(4)}{\rm e}^{{\rm i}h_{+}\sigma_{3}},\end{equation}$
(4.14) $\begin{matrix}&&h_{+}+h_{-}=\left\{\begin{array}{lll} 2\omega_{1}-{\rm i}\ln(\hat{a}_{+}\hat{a}_{-}\delta^{2}{\rm e}^{{\rm i}\theta_{1}}), & \lambda\in \Gamma_{1}\cap{\Bbb C}^{+}, \\ 2\omega_{1}+{\rm i}\ln(\hat{a}_{+}^{\ast}\hat{a}_{-}^{\ast}\delta^{-2}{\rm e}^{-{\rm i}\theta_{1}}), & \lambda\in \Gamma_{1}\cap{\Bbb C}^{-}, \\ 2\omega_{2}-{\rm i}\ln({\rm i}\hat{a}\hat{b}\delta^{2}), & \lambda\in \gamma_{(\varrho,\alpha)}, \\ 2\omega_{2}+{\rm i}\ln(-{\rm i}\hat{a}^{\ast}\hat{b}^{\ast}\delta^{-2}), & \lambda\in \gamma_{(\bar{\alpha},\bar{\varrho})}, \\ -{\rm i}\ln(\nu_{1}^{2}\delta^{2}), & \lambda\in \Gamma_{2}, \end{array}\right.\\&&h_{+}-h_{-}=\left\{\begin{array}{ll} 2\omega_{3}-{\rm i}\ln(aa^{\ast}), & \lambda\in \gamma_{(d,\varrho)}, \\ 2\omega_{3}+{\rm i}\ln(aa^{\ast}), & \lambda\in \gamma_{(\bar{\varrho},d)}, \end{array} \right.\end{matrix}$
其中 $\{\omega_{j}\}_{1}^{3}$ $h_{k}:= h_{+}+h_{-}$
$\bullet$ $\Gamma_{1}\cap{\Bbb C}^{+}$ $\Gamma_{1}\cap{\Bbb C}^{-}$ $\gamma_{(\varrho,\alpha)}$ $\gamma_{(\bar{\alpha},\bar{\varrho})}$ $\Gamma_{2}$
$\bullet$ $\lambda\in {\cal C}\cup\Gamma_{1}\cup\Gamma_{2} \cup\gamma_{(\varrho,\alpha)}\cup\gamma_{(\bar{\alpha},\bar{\varrho})}$ $h_{k}=h_{k}^{\ast}$ .
当 $a(\lambda), b(\lambda)\neq 0$ $\lambda =d$ $\ln(aa^{\ast}) = \ln(|a(d)^{2}|)>0$ $h_{+}-h_{-}$ $\gamma_{(d,\varrho)}$ $\gamma_{(\bar{\varrho},d)}$
对于 $\lambda\in \Gamma^{mod}\setminus {\Bbb C}^{+}$
(4.15) $\begin{matrix}{\cal H}(\lambda)\equiv {\cal H}(\xi,\lambda):=\left\{\begin{array}{ll} \frac{2\omega_{1}-{\rm i}\ln(\hat{a}_{+}\hat{a}_{-}\delta^{2}{\rm e}^{{\rm i}\theta_{1}})}{\omega_{+}}, & \lambda\in \Gamma_{1}\cap{\Bbb C}^{+}, \\[3mm] \frac{2\omega_{2}-{\rm i}\ln({\rm i}\hat{a}\hat{b}\delta^{2})}{\omega_{+}}, & \lambda\in \gamma_{(\varrho,\alpha)}, \\[3mm] \frac{2\omega_{3}-{\rm i}\ln(aa^{\ast})}{\omega}, & \lambda\in \gamma_{(d,\varrho)}, \\[3mm] -\frac{{\rm i}\ln(\delta^{2}\nu_{1}^{2})}{\omega_{+}}, & \lambda\in \Gamma_{2}\cap{\Bbb C}^{+}. \end{array}\right.\end{matrix}$
根据对称性, 函数 ${\cal H}$ $\Gamma^{mod}\setminus {\Bbb C}^{-}$ .
(4.16) $\begin{equation}h(\lambda):=\frac{\omega(\lambda)}{2\pi {\rm i}}\int_{\Gamma^{mod}}\frac{{\cal H}(k)}{k-\lambda}{\rm d}k,~~\lambda\in\overline{{\Bbb C}}\setminus\Gamma^{mod}.\end{equation}$
对于使得函数 $h(\lambda)$ $\omega_{j} \equiv \omega_{j}(\xi)$ $j = 1, 2, 3$
$\bullet$ $h=h^{\ast}$
$\bullet$ $\Gamma^{mod}$
$\bullet$ $\lambda\in\overline{{\Bbb C}}\setminus\Gamma^{mod}$ ${\rm e}^{{\rm i}h\sigma_{3}}$
$\bullet$ $k\rightarrow\infty$ $h(\lambda)=h(\infty)+O\left(\lambda^{-1}\right)$ $h(\infty)=-\frac{1}{2\pi{\rm i}}\int_{\Gamma^{mod}}k^{3}{\cal H}(k){\rm d}k$ .
当 $t\rightarrow\infty$
(4.17) $\begin{matrix}\hat{v}^{(5)}\rightarrow{\Bbb I}, ~~\lambda\in\Gamma^{(5)}\setminus\Gamma^{mod},\end{matrix}$
此外, 解 $\hat{n}^{(5)}$ $n^{mod}$ .
(4.18) $v^{\text {mod }}=\left\{\begin{array}{cc}\left(\begin{array}{cc}0 & \mathrm{ie}^{-2 \mathrm{i}\left(t H_{1}+\omega_{1}\right)} \\ \mathrm{ie}^{2 \mathrm{i}\left(t H_{1}+\omega_{1}\right)} & 0\end{array}\right), \lambda \in \Gamma_{1}, \\ \left(\begin{array}{cc}0 & \mathrm{ie}^{-2 \mathrm{i}\left(t H_{2}+\omega_{2}\right)} \\ \mathrm{ie}^{2 \mathrm{i}\left(t H_{2}+\omega_{2}\right)} & 0\end{array}\right), \lambda \in \gamma_{(\rho, \alpha)} \cup \gamma_{(\bar{\alpha}, \bar{e})}, \\ \left(\begin{array}{cc}\mathrm{e}^{2 \mathrm{i}\left(t H_{3}+\omega_{3}\right)} & 0 \\ 0 & \mathrm{e}^{-2 \mathrm{i}\left(t H_{3}+\omega_{3}\right)}\end{array}\right), & \lambda \in \gamma_{(\bar{\rho}, \underline{e})} \\ \mathrm{i} \sigma_{1}, & \lambda \in \Gamma_{2}.\end{array}\right.$
该矩阵与 $\lambda$ $\lambda\in\gamma_{(\bar{\varrho},\varrho)}$
对于 $\lambda\in{\Bbb C}\setminus\Gamma^{mod}$
随着 $\lambda\rightarrow\infty$ $\nu(\lambda) = 1 + O\left(\lambda^{-1}\right)$ .
定义 $N\rightarrow\overline{{\Bbb C}}$ $\hat{\nu}\equiv\hat{\nu}(\xi,\cdot)$ $\nu^{2}$ $-\nu^{2}$ $N$ $\lambda\in{\Bbb C}\setminus\Gamma^{mod}$ $\hat{\nu}(\lambda^{\pm})=\pm\nu^{2}(\lambda)$ .
若函数 $\hat{\nu}$ $C_{1}$ $\alpha$ $\varrho$ $C_{2}$ $\hat{\nu}$ $\hat{\nu}-1$ $N$ $+\infty$ $D_{1}$ $D_{2}$ $D_{3}$ .
令 $P:=D_{1}D_{2}D_{3}$ . 向量 ${\cal K}$ $l$ $v(t)$
定理 4.1 对任意 $t\geq0$ $\{H_{i},\omega_{i}\}_{1}^{3}$ $n^{mod}(x,t,\lambda)$
(4.19) $\begin{equation}2{\rm i}\lim_{\lambda\rightarrow\infty}\lambda(n^{mod}(x,t,\lambda))_{12}={\rm Im}(C_{1}+C_{2}+\alpha+\varrho)\frac{\Theta\left(\varphi(\infty^{+})+l\right)\Theta\left(\varphi(\infty^{+})-v(t)-l\right)}{\Theta\left(\varphi(\infty^{+})-l\right)\Theta\left(\varphi(\infty^{+})+v(t)+l\right)},\end{equation}$
且关于 $\arg\lambda\in[2\pi]$
(4.20) $\begin{equation}E_{0}(\xi,t)=2{\rm i}{\rm e}^{2{\rm i}(tg(0)+h(\infty))}\lim_{\lambda\rightarrow\infty}\lambda(n^{mod}(x,t,\lambda))_{12}.\end{equation}$
通过对跳跃曲线进行五次变形最终得到 $\hat{n}^{(5)}(x,t,\lambda)$ $\lambda$ $\Gamma^{mod}$ $\lambda$ $\lambda\in D_{\epsilon}(\alpha)$ $\lambda\in D_{\epsilon}(\varrho)$ $\lambda\in D_{\epsilon}(d)$ $\hat{n}^{(5)}(x,t,\lambda)$ $n^{\alpha}(x,t,\lambda)$ $n^{\varrho}(x,t,\lambda)$ $n^{d}(x,t,\lambda)$
当 $\lambda\in D_{\epsilon}(\alpha)\setminus\Gamma^{(5)}$
(4.21) $\begin{equation}n^{(\alpha_{0})}(x,t,\lambda):=\hat{n}^{(5)}(x,t,\lambda){\rm e}^{\left[\frac{{\rm 1}}{2}\ln\left(-\delta(\lambda)^{2}\hat{a}(\lambda)\hat{b}(\lambda)\right)-{\rm i}\left(tg(\alpha)+h(\lambda)\right)\right]\sigma_{3}},\end{equation}$
当 $\lambda\in D_{\epsilon}(\alpha)\setminus\gamma_{(\varrho,\alpha)}$ $g_{\alpha}(\lambda)\equiv g_{\alpha}(\xi,\lambda):=g(\lambda)-g(\alpha)$ .
开集 $D_{\epsilon}(\alpha)$ $\alpha$ ${\cal S}_{i}$ $\left\{{\cal S}_{i}\right\}_{1}^{4}$ $\left\{{\cal Y}_{i}\right\}_{1}^{4}$ ${\cal Y}_{i} = \overline{{\cal S}}_{i-1}\cap\overline{{\cal S}}_{i}$ $i = 1, \cdots, 4$ $\overline{{\cal S}}_{0}\equiv \overline{{\cal S}}_{4}$ . 具体分布图如图4 .4 所示.
图4.4
图4.4
开集 $D_{\epsilon}(\alpha)$ $\{{\cal S}_{i}\}_{1}^{4}$
鉴于(4.3)式中跳跃矩阵 $\hat{v}^{(5)}$ $n^{(\alpha_{0})}$
对于 $\lambda\in D_{\epsilon}(\alpha)$
(4.22) $\begin{matrix}&&\varpi\equiv\varpi(\lambda):=\left(\frac{3{\rm i}t}{2}g_{\alpha}(\lambda)\right)^{2/3},\\&&g_{\alpha}(\lambda) = \int_{\alpha}^{\lambda}\sqrt{k-\alpha}f(k){\rm d}k,\end{matrix}$
其中$f(\lambda)$ $\lambda= \alpha$
(4.23) $\begin{matrix}\varpi:=\left(\frac{3t}{2}\right)^{2/3}(\lambda-\alpha)\psi_{\alpha}(\lambda),\end{matrix}$
这里, 当 $\lambda\in D_{\epsilon}(\alpha)$ $\psi_{\alpha}(\lambda)\equiv\psi_{\alpha}(\xi,\lambda)$ $\psi_{\alpha}(\alpha)\neq0$ .
根据(4.23)式, 圆盘 $D_{\epsilon}(\alpha)$ $\lambda\mapsto\xi$ .
由于在跳跃曲线 $\gamma(\varrho,\alpha)$ ${\rm Im} g_{\alpha}(\alpha)$ ${\cal Y}_{3}$ $\mathbb{R} _{-}$ $\lambda\mapsto\xi$ ${\cal Y}_{3}$ $\xi$
方程(4.22)可进一步变形为 $\frac{4}{3}\varpi^{3/2}:=2{\rm i}tg_{\alpha}(\lambda)$ . $n^{(\alpha0)}(\lambda)$ $n^{Ai}(\varpi(\lambda))$ $\alpha$
接下来定义在 $\alpha$ $\hat{n}^{(5)}$
(4.24) $\begin{matrix}n^{\alpha}(x,t,\lambda)=Y_{\alpha}(x,t,\lambda)n^{Ai}(\varpi(\lambda)){\rm e}^{\left[-\frac{1}{2}\ln(-\delta^{2}\hat{a}\hat{b})+{\rm i}\left(tg(\alpha)+h(\lambda)\right)\right]\sigma_{3}},~~\lambda\in D_{\epsilon}(\alpha)\setminus\Gamma^{(5)},\end{matrix}$
(4.25) $\begin{matrix}Y_{\alpha}(x,t,\lambda):=n^{mod}{\rm e}^{\left[-\frac{1}{2}\ln(-\delta^{2}\hat{a}\hat{b})+{\rm i}\left(tg(\alpha)+h(\lambda)\right)\right]\sigma_{3}}n_{as,M}^{Ai}(\varpi(\lambda)),~~M\geq0\end{matrix}$
在 $D_{\epsilon}(\alpha)$
当 $\lambda\in {\cal Y}_{3}$ $n_{as,M}^{Ai}(\varpi(\lambda))$
(4.26) $\begin{matrix}\left(n_{as,M}^{Ai}(\varpi(\lambda))\right)_{-}={\rm i}\sigma_{2}\left(n_{as,M}^{Ai}(\varpi(\lambda))\right)_{+}.\end{matrix}$
鉴于 $n^{mod}$ $n^{mod}{\rm e}^{\left[-\frac{1}{2}\ln(-\delta^{2}\hat{a}\hat{b})+{\rm i}\left(tg(\alpha)+h(\lambda)\right)\right]\sigma_{3}}$ ${\cal Y}_{\alpha}$ $D_{\epsilon}(\alpha)$
(4.27) $\begin{matrix}n^{\alpha}(\lambda)n^{mod}(\lambda)^{-1}={\Bbb I}+O(t^{-M-1}),~~t\rightarrow\infty,~\lambda\in\partial D_{\epsilon}(\alpha),\end{matrix}$
并且对于 $\lambda\in\partial D_{\epsilon}(\alpha)$
当 $\lambda\in D_{\epsilon}(\varrho)\setminus\Gamma^{(5)}$
(4.28) $\begin{matrix}n^{(\varrho_{0})}(x,t,\lambda):=\hat{n}^{(5)}(x,t,\lambda){\rm e}^{\left[\frac{1}{2}\ln\left(\delta(\lambda)^{2}\hat{a}(\lambda)\hat{b}(\lambda)\right)-{\rm i}h(\lambda)\right]\sigma_{3}},\end{matrix}$
开集 $D_{\epsilon}(\varrho)$ $\varrho$ ${\cal T}_{i}$ $\left\{{\cal T}_{i}\right\}_{1}^{5}$ $\left\{{\cal Z}_{i}\right\}_{1}^{5}$ ${\cal Z}_{i} = \overline{{\cal T}}_{i-1}\cap\overline{{\cal T}}_{i}$ $i = 1, \cdots, 5$ $\overline{{\cal T}}_{0}\equiv \overline{{\cal T}}_{5}$ . 具体分布图如图4 .5 所示.
图4.5
图4.5
开集 $D_{\epsilon}(\varrho)$ $\{{\cal T}_{i}\}_{1}^{5}$
基于(4.13)式中跳跃矩阵 $\hat{v}^{(5)}$ $n^{(\varrho_{0})}$
对于 $\lambda\in D_{\epsilon}(\varrho)\setminus(\gamma_{\bar{\varrho},\varrho}\cup\gamma_{\varrho,\alpha})$ $g_{\varrho}(\lambda)\equiv g_{\varrho}(\xi,\lambda)$
进而, 函数 $n^{(\varrho_{1})}(x,t,\lambda)$ $n^{(\varrho_{0})}(x,t,\lambda)$
可得出 $n^{(\varrho_{1})}$ $n_{+}^{(\varrho_{1})} = n_{-}^{(\varrho_{1})}v^{(\varrho_{1})}$
与 $\lambda$ $\alpha$ $\lambda\in D_{\epsilon}(\varrho)\setminus\Gamma^{(5)}$
(4.29) $\begin{matrix}n^{\varrho}(x,t,\lambda)=Y_{\varrho}(x,t,\lambda)n^{Ai}(\varpi(\lambda))A(\lambda)^{-1}\times{\rm e}^{\left[\frac{1}{2}\ln\left(\delta(\lambda)^{2}\hat{a}(\lambda)\hat{b}(\lambda)\right)-{\rm i}h(\lambda)\right]\sigma_{3}},\end{matrix}$
(4.30) $\begin{matrix}Y_{\varrho}(x,t,\lambda):=n^{mod}{\rm e}^{\left[\frac{1}{2}\ln\left(\delta(\lambda)^{2}\hat{a}(\lambda)\hat{b}(\lambda)\right)-{\rm i}h(\lambda)\right]\sigma_{3}}A(\lambda)(n_{as,M}^{Ai}(\varpi(\lambda)))^{-1},~~M\geq0\end{matrix}$
在 $D_{\epsilon}(\varrho)$
对于 $\lambda\in {\cal Z}_{3}$ $\left(n_{as,M}^{Ai}(\varpi(\lambda))\right)_{+}=-{\rm i}\sigma_{2}\left(n_{as,M}^{Ai}(\varpi(\lambda))\right)_{-}$ .
因此, 结合(4.29)及(4.30)式, 可推导出
(4.31) $\begin{matrix}n^{\varrho}(\lambda)n^{mod}(\lambda)^{-1}={\Bbb I}+O\left(t^{-M-1}\right),~~t\rightarrow\infty,~\lambda\in\partial D_{\epsilon}(\varrho),\end{matrix}$
并且关于 $\lambda\in D_{\epsilon}(\varrho)$
开集 $D_{\epsilon}(d)$ $d$ ${\cal R}_{i}$ $\left\{{\cal R}_{i}\right\}_{1}^{6}$ $\left\{{\cal X}_{i}\right\}_{1}^{6}$ ${\cal X}_{i} = \overline{{\cal R}}_{i-1}\cap \overline{{\cal R}}_{i}$ $i = 1, \cdots, 6$ $\overline{{\cal R}}_{0}\equiv\overline{{\cal R}}_{6}$ . 具体分布如图4 .6 所示.
图4.6
图4.6
开集 $D_{\epsilon}(d)$ $\{{\cal R}_{i}\}_{1}^{6}$
对于 $\lambda\in D_{\epsilon}(d)$
(4.32) $\begin{matrix}B(\lambda)\equiv B(\xi, \lambda):=\left\{\begin{array}{cc} {\rm e}^{-{\rm i}tg_{-}(d)\sigma_{3}}, & \lambda\in {\cal R}_{1}\cup{\cal R}_{2}\cup{\cal R}_{6}, \\ {\rm e}^{-{\rm i}tg_{+}(d)\sigma_{3}}, & \lambda\in {\cal R}_{3}\cup{\cal R}_{4}\cup{\cal R}_{5}. \end{array} \right.\end{matrix}$
进一步地, 对于 $\lambda\in D_{\epsilon}(d)\setminus\Gamma^{(5)}$ $n^{(d_{0})}(x,t,\lambda):=\hat{n}^{(5)}(x,t,\lambda){\rm e}^{-{\rm i}h\sigma_{3}}B(\lambda),$ $n_{+}^{(d_{0})}=n_{-}^{(d_{0})}v^{(d_{0})}$ $v^{(d_{0})}$
为了去除跳跃曲线 $\gamma_{(\bar{\varrho},\varrho)}$
(4.33) $\begin{equation}\tilde{\delta}(\xi,\lambda)\equiv\tilde{\delta}(\lambda):=\exp\left\{\frac{1}{2\pi {\rm i}}\left(\int_{\gamma_{(\bar{\varrho},d)}}\frac{\ln(a(k)\overline{a(\bar{k})})}{k-\lambda}{\rm d}k\!-\!\int_{\gamma_{(d,\varrho)}}\frac{\ln(a(k)\overline{a(\bar{k})})}{k-\lambda}{\rm d}k\right)\right\},\lambda\in {\Bbb C}\setminus\gamma_{(\bar{\varrho},\varrho)}.\end{equation}$
$\bullet$ $\ln(a(k)\overline{a(\bar{k})})$
$\bullet$ $k = d$
由于 $a(\lambda)$ $aa^{\ast}$ $\tilde{\delta}$ $\varrho$ $\bar{\varrho}$ $d$
首先介绍函数 $\tilde{\delta}$
$\bullet$ $\lambda\in D_{\epsilon}(d)\setminus\gamma_{(\bar{\varrho},\varrho)}$ $\tilde{\delta}(\lambda)$ $\tilde{\delta}(\lambda)^{-1}$
$\bullet$ $\lambda\in {\Bbb C}\setminus\gamma_{(\bar{\varrho},\varrho)}$ $\tilde{\delta}=(\tilde{\delta}^{\ast})^{-1}$
$\bullet$ $\tilde{\delta}_{+}=\tilde{\delta}_{-}\times\left\{\begin{array}{ll} (aa^{\ast})^{-1},~ & \lambda\in \gamma_{(d,\varrho)}, \\ aa^{\ast},~ & \lambda\in \gamma_{(\bar{\varrho},d)}. \end{array}\right.$
然后, 定义$n^{(d_{1})}(x,t,\lambda):=n^{(d_{0})}(x,t,\lambda)\tilde{\delta}(\lambda)^{-\sigma_{3}},~~\lambda\in D_{\epsilon}(d),$ $n_{+}^{(d_{1})}=n_{-}^{(d_{1})}v^{(d_{1})}$
(4.34)
在复平面 $z$ $D_{\epsilon}(d)$ $\lambda\mapsto z$
首先, 引入一个新的变量 $z \equiv z(\lambda):=\sqrt{tg_{d}(\lambda)}$ .
由于 $g_{d}(\lambda)$ $\lambda = d$ $z={\rm i}\sqrt{t}(\lambda-d)\psi_{d}(\lambda)$ .
对于 $\lambda\in D_{\epsilon}(d)$ $\psi_{d}(\lambda)\equiv \psi_{d}(\xi,\lambda)$ $\frac{\partial g}{\partial\lambda}$ $\frac{\partial^{2} g}{\partial\lambda^{2}}< 0$ .
进而, 跳跃曲线必须满足条件: $\psi_{d}(d) > 0$ .
对于 $\lambda\in \overline{D_{\epsilon}(d)}$ ${\rm Re} d(\lambda) > 0$ $2{\rm i}tg_{d}(\lambda)=2{\rm i}z^{2}$ .
集合 $D_{\epsilon}(d)$ $\lambda\mapsto z$ . 通过一系列变形分别将跳跃曲线 ${\cal X}_{3}$ ${\cal X}_{6}$ $\mathbb{R} _{-}$ $\mathbb{R} _{+}$ ${\cal X}_{1}$ ${\cal X}_{2}$ ${\cal X}_{4}$ ${\cal X}_{5}$ $z$ $\arg z$ $\frac{\pi}{4}$ $\frac{3\pi}{4}$ $-\frac{3\pi}{4}$ $-\frac{\pi}{4}$ .
接下来, 将分析当 $\lambda$ $d$ $\tilde{\delta}$
函数 $\ln(\lambda-d)$ $\gamma_{(d,\varrho)}$ $\gamma_{(d,\bar{\varrho})}$
其中, 对于 $\lambda> d$ $\ln_{\varrho}(\lambda-d)$ $\ln_{\bar{\varrho}}(\lambda-d)$
$\bullet$ $\lambda\in D_{\epsilon}\setminus\gamma_{(d,\varrho)}$ $L_{\varrho}(k,\lambda)$ $k\in \gamma_{(d,\varrho)}$
$\bullet$ $\lambda\in D_{\epsilon}\setminus\gamma_{(\bar{\varrho},d)}$ $L_{\bar{\varrho}}(k,\lambda)$ $k\in \gamma_{(\bar{\varrho},d)}$
$\bullet$ $k= d$ $L_{\varrho}(d,\lambda) = \ln_{\varrho}(\lambda-d),~~L_{\bar{\varrho}}(d,\lambda) = \ln_{\bar{\varrho}}(\lambda-d)$ .
基于 $\tilde{\delta}(\lambda)$ $\delta(\lambda)$
当 $a=-\pi$ $\ln_{-\pi}\lambda= \ln\lambda$ .
定义函数$p(z)\equiv p(\xi, z):={\rm e}^{-{\rm i}\nu[\ln_{-\pi/2}(z)-\ln z-\ln_{0}(z)]},~ z\in{\Bbb C}\setminus(\mathbb{R} \cup {\rm i}\mathbb{R} _{-}).$ $\delta_{0}(t)$ $\delta_{1}(\lambda)$ $\delta_{2}(\lambda)$
定义跳跃曲线 $X := X_{1}\cup X_{2}\cup X_{3}\cup X_{4}\subset{\Bbb C}$ $X_{1}:=\{k{\rm e}^{\frac{{\rm i}\pi}{4}}| 0\leq k<\infty\}$ $X_{2}:=\{k{\rm e}^{\frac{3{\rm i}\pi}{4}}| 0\leq k<\infty\}$ $X_{3}:=\{k{\rm e}^{-\frac{3{\rm i}\pi}{4}}| 0\leq k<\infty\}$ $X_{4}:=\{k{\rm e}^{-\frac{{\rm i}\pi}{4}}| 0\leq k<\infty\}$ 图4 .7 所示.
图4.7
函数 $\rho(u, z):= {\rm e}^{{\rm i}\nu(u)\ln_{-\pi/2}z}$ $z^{i\nu(u)}$ $\nu(u):=\frac{1}{2\pi}\ln(1+|u|^{2})$ .
定义一个新的 Riemann-Hilbert 问题
(4.35) $\begin{equation}\left\{\begin{array}{ll} n^{X}(u,\cdot)\in {\Bbb I}+\dot{E}^{2}({\Bbb C}\setminus X),\\ n^{X}_{+}(u,z)=n^{X}_{-}(u,z)v^{X}(u,z), ~z\in X, \end{array}\right.\end{equation}$
(4.36) $v^{X}(u, z):=\left\{\begin{array}{ll}\left(\begin{array}{cc}1 & 0 \\ u \rho(u, z)^{-2} \mathrm{e}^{2 \mathrm{i} z^{2}} & 1\end{array}\right), & \lambda \in X_{1}, \\ \left(\begin{array}{cc}1 & \bar{u} \rho(u, z)^{2} \mathrm{e}^{-2 \mathrm{i} z^{2}} \\ 0 & 1\end{array}\right), & \lambda \in X_{2}, \\ \left(\begin{array}{cc}u \\ -\frac{u}{1+|u|^{2}} \rho(u, z)^{-2} \mathrm{e}^{2 \mathrm{i} z^{2}} & 1\end{array}\right), & \lambda \in X_{3}, \\ \left(\begin{array}{cc}1 & -\frac{\bar{u}}{1+|u|^{2}} \rho(u, z)^{2} \mathrm{e}^{-2 \mathrm{i} z^{2}} \\ 0 & 1\end{array}\right), & \lambda \in X_{4}.\end{array}\right.$
值得注意的是, 矩阵 $v^{X}(u,z)$
当 $z\rightarrow0$ $v^{X}(u,\cdot)-{\Bbb I}\in L^{2}(X)\setminus L^{\infty}(X)$ .
根据抛物线柱面函数[44 ]}, 可知 Riemann-Hilbert 问题(4.35)有显式解.
对于 $\lambda\in D_{\epsilon}(d)\setminus\Gamma^{(5)}$ $X$
且关于 $z$
给定 $z$ $t\rightarrow\infty$ $\hat{r}(\lambda(z))\rightarrow u$ $\delta_{1}(\lambda(z))\rightarrow1$ . 这表明当 $t$ $v^{(d_{2})}$ $v^{X}$ .
因此, 对于 $\lambda\in D_{\epsilon}(d)$ $t\rightarrow\infty$ $\hat{n}^{(5)}\rightarrow n^{X}\delta_{0}^{-\sigma_{3}}\tilde{\delta}^{\sigma_{3}}B(\lambda)^{-1}{\rm e}^{{\rm i}h\sigma_{3}}$ .
为了更好地逼近 $\hat{n}^{(5)}$
(4.37) $\begin{matrix}n^{d}(x,t,\lambda)=Y_{d}(x,t,\lambda)n^{X}(u,z(\lambda))\delta_{0}(t)^{-\sigma_{3}}\tilde{\delta}(\lambda)^{\sigma_{3}}B(\lambda)^{-1}{\rm e}^{{\rm i}h\sigma_{3}},\end{matrix}$
(4.38) $\begin{matrix}Y_{d}(x,t,\lambda):=n^{mod}(x,t,\lambda){\rm e}^{-{\rm i}h(\lambda)\sigma_{3}}B(\lambda)\tilde{\delta}(\lambda)^{-\sigma_{3}}\delta_{0}(t)^{\sigma_{3}}\end{matrix}$
当 $\lambda\in D_{\epsilon}(d)$ $f(\lambda) :=n^{mod}(x,t,\lambda){\rm e}^{-{\rm i}h(\lambda)\sigma_{3}}$ ${\cal X}_{3}\cup {\cal X}_{6}$
由(4.32)和(4.34)式可推断 $\tilde{\delta}(\lambda)^{\sigma_{3}}B(\lambda)^{-1}$ ${\cal X}_{3}\cup {\cal X}_{6}$ $\lambda\in D_{\epsilon}(d)$ $Y_{d}$
集合 $\Gamma^{(5)}$ $D_{\epsilon}(d)$ ${\cal X}:={\cal X}_{1}\cup{\cal X}_{2}\cup {\cal X}_{4}\cup {\cal X}_{5}$ $\gamma_{(\bar{\varrho},\varrho)}\cap D_{\epsilon}(d)={\cal X}_{3}\cup {\cal X}_{6}$ .
对于 $\lambda\in D_{\epsilon}(d)\setminus\Gamma^{(5)}$ $n^{d}(x,t,\lambda)$
对于 $\lambda\in D_{\epsilon}(d)$ $Y_{d}(x,t,\lambda)$
因此, 当$\lambda\in\gamma_{(\bar{\varrho},\varrho)}\cap D_{\epsilon}(d)$ $n^{d}$ $n_{+}^{d}=n_{-}^{d}v^{d}$ $v^{d}=\hat{v}^{(5)}$ .
进一步地, 随着 $t\rightarrow\infty$
(4.39) $\begin{matrix}\left\{\begin{array}{ll} \|\hat{v}^{(5)}-v^{d}\|_{L^{1}(\chi)}=O\left(t^{-1}\ln t\right), \\ \|\hat{v}^{(5)}-v^{d}\|_{L^{2}(\chi)}=O\left(t^{-3/4}\ln t\right), \\ \|\hat{v}^{(5)}-v^{d}\|_{L^{\infty}(\chi)}=O\left(t^{-1/2}\ln t\right). \end{array} \right.\end{matrix}$
此外, 当 $\lambda\in\partial D_{\epsilon}(d)$ $n^{mod}(n^{d})^{-1}$
(4.40) $\begin{matrix}\|n^{mod}(n^{d})^{-1}-{\Bbb I}\|_{L^{\infty}(\partial D_{\epsilon}(d))}=O\big(t^{-1/2}\big).\end{matrix}$
随着 $t\rightarrow\infty$
(4.41) $n_{1}^{X}(\xi) \equiv n_{1}^{X}:=\left(\begin{array}{cc}0 & -\mathrm{e}^{\pi \nu} \varrho^{X}(u) \\ \mathrm{e}^{\pi \nu} \overline{\varrho^{X}(u)} & 0\end{array}\right)$
(4.42) $\begin{matrix}E_{1}(\xi,t)=-2{\rm i}{\rm e}^{2{\rm i}(tg(0)+h(\infty))}\frac{\left(Y_{d}(x,t,d)n_{1}^{X}Y_{d}(x,t,d)^{-1}\right)_{12}}{\psi_{d}(d)}.\end{matrix}$
基于上述分析, 局部解 $n^{\bar{\alpha}}(x,t,\lambda)$ $n^{\bar{\varrho}}(x,t,\lambda)$
记五个开集的并为 ${\cal D}$ . 更具体地,${\cal D}=D_{\epsilon}(\bar{\alpha})\cup D_{\epsilon}(\bar{\varrho})\cup D_{\epsilon}(\varrho)\cup D_{\epsilon}(\alpha)\cup D_{\epsilon}(d)$ .
其满足 Riemann-Hilbert 问题, 且跳跃曲线为
图4.8
图4.8
跳跃曲线 $\Gamma^{app}$ ${\rm Im} g <0$ ${\rm Im} g >0$
具体分布如图4 .9所示.函数 $\tilde{n}(x,t,\lambda)$ $\tilde{n}:=\hat{n}^{(5)}(n^{app})^{-1}$ $t\rightarrow\infty$ $\tilde{n}\rightarrow{\Bbb I}$ $\lambda\in \tilde{\Gamma}$
图4.9
图4.9
跳跃曲线 $\tilde{\Gamma}$ ${\rm Im} g <0$ ${\rm Im} g >0$
设 $\hat{\omega}=\tilde{v}-{\Bbb I}$ . 当 $t\rightarrow\infty$ $\hat{v}^{(5)}-{\Bbb I}$ $\Gamma^{(5)}\setminus\Gamma^{mod}$
(4.43) $\begin{matrix}\|\hat{\omega}\|_{(L^{1}\cap L^{2}\cap L^{\infty})(\tilde{\Gamma}\setminus\bar{{\cal D}})}=O\left({\rm e}^{-bt}\right),~~t\rightarrow\infty,\end{matrix}$
其中 $b \equiv b(\xi) > 0$ .
(4.44) $\begin{matrix}\|\hat{\omega}\|_{L^{\infty}(\partial D_{\epsilon}(\alpha)\cup\partial D_{\epsilon}(\varrho)\cup\partial D_{\epsilon}(\bar{\alpha})\cup\partial D_{\epsilon}(\bar{\varrho}))}=O\left(t^{-M}\right),~~t\rightarrow\infty,~~\forall M \geq 1.\end{matrix}$
(4.45) $\begin{equation}\|\hat{\omega}\|_{L^{\infty}(\partial D_{\epsilon}(d))}=O\big(t^{-1/2}\big),~~t\rightarrow\infty.\end{equation}$
对于 $\lambda\in{\cal X}$ $\hat{\omega}=n_{-}^{d}(\hat{v}^{(5)}-v^{d})(n_{+}^{d})^{-1}$ .
根据(4.39)式, 随着 $t\rightarrow\infty$
(4.46) $\begin{matrix}\left\{\begin{array}{ll} \|\hat{\omega}\|_{L^{1}(\chi)}=O\left(t^{-1}\ln t\right), \\ \|\hat{\omega}\|_{L^{2}(\chi)}=O\left(t^{-3/4}\ln t\right), \\ \|\hat{\omega}\|_{L^{\infty}(\chi)}=O\left(t^{-1/2}\ln t\right). \end{array} \right.\end{matrix}$
由(4.43), (4.44), (4.45)以及(4.46)式可知
进而, 对于 $\lambda\in{\Bbb C}\setminus\tilde{\Gamma}$ $(\hat{{\cal C}}f)(\lambda)=\frac{1}{2\pi {\rm i}}\int_{\tilde{\Gamma}}\frac{f(k)}{k-\lambda}{\rm d}k$ $\tilde{\Gamma}$ $\hat{{\cal C}}_{\pm}f$ . 根据文献[42 ]可知柯西算子的定义 $\hat{{\cal C}}_{\hat{\omega}}: L^{2}(\tilde{\Gamma})\rightarrow L^{2}(\tilde{\Gamma})$ $\hat{{\cal C}}_{\hat{\omega}}f = \hat{{\cal C}}_{-}(f\hat{\omega})$ .
当 $t\rightarrow\infty$ $ \|\hat{{\cal C}}_{\hat{\omega}}\|_{{\cal B}(L^{2}(\tilde{\Gamma}))}\leq C\|\hat{\omega}\|_{L^{\infty}(\tilde{\Gamma})}=O\left(t^{-1/2}\ln t\right)$ . 特别地, ${\Bbb I}-\hat{{\cal C}}_{\hat{\omega}}(\xi,t,\cdot)\in B\big(L^{2}(\tilde{\Gamma})\big)$
对于 $\hat{d}(x, t,\lambda)\in{\Bbb I}+L^{2}(\tilde{\Gamma})$ $\hat{d}:={\Bbb I}+({\Bbb I}-\hat{{\cal C}}_{\hat{\omega}})^{-1}\hat{{\cal C}}_{\hat{\omega}}$ .
当 $t\rightarrow\infty$
(4.47) $\begin{equation}\|\hat{d}(x,t,\cdot)-{\Bbb I}\|_{L^{2}(\tilde{\Gamma})}=O\big(t^{-1/2}\big).\end{equation}$
此外, 近似解 $\tilde{n}(x,t,\lambda)$
由于 $\hat{\omega}$ $\lambda\rightarrow\infty$
(4.48) $\begin{matrix}\lim_{\lambda\rightarrow\infty}\lambda\left(\tilde{n}(x,t,\lambda)-{\Bbb I}\right)=-\frac{1}{2\pi {\rm i}}\int_{\tilde{\Gamma}}\hat{d}(x,t,k)\hat{\omega}(x,t,k){\rm d}k,\end{matrix}$
关于 $\arg \lambda\in [2\pi]$
综上所述, 近似解 $\hat{n}(x,t,\lambda)$
基于(4.2)式, 聚焦 KE 方程(1.2)的解 $u(x,t)$
5 结论
本文研究了聚焦 KE 方程(1.2)在无穷远处初值为两个不同的平面波形式(1.3)下解的长时间渐进性. 首先将柯西问题转化成基本的 Riemann-Hilbert 问题, 然后通过对该问题的跳跃曲线进行一系列的变形, 将其转化为可解的矩阵 Riemann-Hilbert 问题. 利用非线性速降法, 最终得到不同情况下的渐近解.所研究的非线性可积系统由于参数 $\beta$
非局部可积系统是近年来数学物理领域研究的热点之一, 因此, 值得注意的是, 非局部 NLS 型方程解的长时间渐进性是否可以用非线性速降法进行分析? 这些问题将留待以后讨论.
参考文献
View Option
[1]
Zakharov V E . Stability of periodic waves of finite amplitudeon the surfaceof a deepfluid
J Appl Mech Tech Phys , 1968 , 9 190 -194
DOI:10.1007/BF00913182
URL
[本文引用: 1]
[2]
Agrawal G P . Nonlinear Fiber Optics . New York : Academic Press , 1995
[本文引用: 1]
[3]
Bao W Z Dong X C Xin J . Comparisons between sine-Gordon and perturbed nonlinear Schrödinger equations for modeling light bullets beyond critical collapse
Physica D , 2010 , 239 1120 -1134
DOI:10.1016/j.physd.2010.03.002
URL
[本文引用: 1]
[4]
Hasegawa A Kodama Y . Solitons in Optical Communications . Oxford : Oxford University Press , 1995
[本文引用: 1]
[5]
Akhmediev N Ankiewicz A . Solitons: Nonlinear Pulses and Beams . London : Chapmanand Hall , 1997
[本文引用: 1]
[6]
Pitaevskii L Stringari S . Bose-Einstein Condensation . Oxford : Oxford University Press , 2003
[本文引用: 1]
[7]
Antoine X Bao W Z Besse C . Computational methods for the dynamics of the nonlinear Schrödinger/Gross-Pitaevskii equations
Computer Physics Communications , 2013 , 184 2621 -2633
DOI:10.1016/j.cpc.2013.07.012
URL
[本文引用: 1]
[9]
Kundu A . Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations
J Math Phys , 1984 , 25 3433
DOI:10.1063/1.526113
URL
[本文引用: 1]
New Landau–Lifshitz (LL) and higher-order nonlinear systems gauge generated from nonlinear Schrödinger (NS) type equations are presented. The consequences of gauge equivalence between different dynamical systems are discussed. The gauge connections among various LL and NS equations are found and depicted through a schematic representation.
[11]
Matveev V B Salle M A . Darboux Transformations and Solitons . Berlin : Springer , 1991
[本文引用: 1]
[13]
Geng X G Tam H W . Darboux transformation and soliton solutions for generalized nonlinear Schrödinger equations
J Phys Soc Jpn , 1999 , 68 1508
DOI:10.1143/JPSJ.68.1508
URL
[本文引用: 1]
[14]
Zhao L C Liu C Yang Z Y . The rogue waves with quintic nonlinearity and nonlinear dispersion effects in nonlinear optical fibers
Commun Nonlinear Sci Numer Simul , 2015 , 20 9 -13
DOI:10.1016/j.cnsns.2014.04.002
URL
[本文引用: 1]
[16]
Wang G X Wang X B Han B Xue Q . Inverse scattering method for the Kundu-Eckhaus equation with zero/nonzero boundary conditions
Z Naturforsch A , 2021 , 76 4 ): 315 -327
DOI:10.1515/zna-2020-0327
URL
[本文引用: 1]
In this paper, the inverse scattering approach is applied to the Kundu-Eckhaus equation with two cases of zero boundary condition (ZBC) and nonzero boundary conditions (NZBCs) at infinity. Firstly, we obtain the exact formulae of soliton solutions of three cases of N simple poles, one higher-order pole and multiple higher-order poles via the associated Riemann-Hilbert problem (RHP). Moreover, given the initial data that allow for the presence of discrete spectrum, the higher-order rogue waves of the equation are presented. For the case of NZBCs, we can construct the infinite order rogue waves through developing a suitable RHP. Finally, by choosing different parameters, we aim to show some prominent characteristics of this solution and express them graphically in detail. Our results should be helpful to further explore and enrich the related nonlinear wave phenomena.
[17]
Ablowitz M J Segur H . Solitons and the Inverse Scattering Transform
Philadelphia: SIAM , 1981
[本文引用: 1]
[18]
Ablowitz M J Feng B F Luo X D Musslimani Z H . Inverse scattering transform for the nonlocal reverse space-time nonlinear Schrödinger equation
Theor Math Phys , 2018 , 196 3 ): 1241 -1267
DOI:10.1134/S0040577918090015
[本文引用: 1]
[20]
Ma W X Huang Y H Wang F D . Inverse scattering transforms and soliton solutions of nonlocal reverse-space nonlinear Schrödinger hierarchies
Stud Appl Math , 2020 , 145 563 -585
DOI:10.1111/sapm.v145.3
URL
[本文引用: 1]
[21]
Deift P Zhou X . A steepest descent method for oscillatory Riemann-Hilbert problems
Ann Math , 1993 , 137 2 ): 295 -368
DOI:10.2307/2946540
URL
[本文引用: 4]
[22]
Deift P Venakides S Zhou X . The collisionless shock region for the long-time behavior of solutions of the KdV equation
Commun Pure Appl Math , 1994 , 47 2 ): 199 -206
DOI:10.1002/(ISSN)1097-0312
URL
[本文引用: 2]
[23]
De Monvel A B Lenells J Shepelsky D . The focusing NLS equation with step-like oscillating background: scenarios of long-time asymptotics
Commun Math Phys , 2021 , 383 893 -952
DOI:10.1007/s00220-021-03946-x
[本文引用: 2]
[24]
De Monvel A B Lenells J Shepelsky D . The focusing NLS equation with step-like oscillating background: the genus 3 sector
Commun Math Phys , 2022 , 390 3 ): 1081 -1148
DOI:10.1007/s00220-021-04288-4
[本文引用: 1]
[25]
De Monvel A B Kotlyarov V P Shepelsky D . Focusing NLS equation: long-time dynamics of step-like initial data
Int Math Res Not , 2011 , 7 1613 -1653
[本文引用: 2]
[26]
De Monvel A B Its A Kotlyarov V . Long-time asymptotics for the focusing NLS equation with time-periodic boundary condition on the half-line
Comm Math Phys , 2009 , 290 479 -522
DOI:10.1007/s00220-009-0848-7
URL
[本文引用: 1]
[27]
Buckingham R Venakides S . Long-time asymptotics of the nonlinear Schrödinger equation Shock problem
Comm Pure Appl Math , 2007 , 60 9 ): 1349 -1414
DOI:10.1002/(ISSN)1097-0312
URL
[本文引用: 2]
[28]
Biondini G Mantzavinos D . Long-time asymptotics for the focusing nonlinear Schrödinger equation with nonzero boundary conditions at infinity and asymptotic stage of modulational instability
Comm Pure Appl Math , 2017 , 70 12 ): 2300 -2365
DOI:10.1002/cpa.v70.12
URL
[本文引用: 2]
[29]
Biondini G Fagerstrom E . The integrable nature of modulational instability
SIAM J Appl Math , 2015 , 75 136 -163
DOI:10.1137/140965089
URL
[本文引用: 1]
[31]
Xu J Fan E G Chen Y . Long-time asymptotic for the derivative nonlinear Schrödinger equation with step-like initial value
Math Phys Anal Geom , 2013 , 16 253 -288
DOI:10.1007/s11040-013-9132-3
URL
[本文引用: 1]
[32]
Yamane H . Long-time asymptotics for the defocusing integrable discrete nonlinear Schrödinger equation
J Math Soc Jpn , 2014 , 6 765 -803
[本文引用: 1]
[33]
Lenells J . The nonlinear steepest descent method: asymptotics for initial-boundary value problems
SIAM J Math Anal , 2016 , 48 2076 -2118
DOI:10.1137/15M1036889
URL
[本文引用: 1]
[35]
Tian S F Zhang T T . Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schrödinger equation with time-periodic boundary condition
P Am Math Soc , 2018 , 146 4 ): 1713 -1729
[本文引用: 1]
[37]
Wang X B Han B . The nonlinear steepest descent approach for long time behavior of the two-component coupled Sasa-Satsuma equation with a $5\times5$
Taiwanese J Math , 2021 , 25 2 ): 381 -407
[本文引用: 1]
[38]
Wang X B Han B . A Riemann-Hilbert approach to a generalized nonlinear Schrödinger equation on the quarter plane
Math Phys Anal Geom , 2020 , 23 25
DOI:10.1007/s11040-020-09347-1
[本文引用: 2]
[39]
Guo B L Nan L . Long-time asymptotics for the Kundu-Eckhaus equation on the half-line
J Math Phys , 2018 , 59 061505
DOI:10.1063/1.5020996
URL
[本文引用: 2]
[40]
Wang D S Wang X L . Long-time asymptotics and the bright $N$ - soliton solutions of the Kundu-Eckhaus equation via the Riemann-Hilbert approach
Nonlinear Anal Real World Appl , 2018 , 41 334 -361
DOI:10.1016/j.nonrwa.2017.10.014
URL
[本文引用: 2]
[41]
Wang D S Guo B L Wang X L . Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions
J Differential Equations , 2019 , 266 5209 -5253
DOI:10.1016/j.jde.2018.10.053
URL
[本文引用: 2]
[43]
Lenells J . Matrix Riemann-Hilbert problems with jumps across Carleson contours
Monatsh Math , 2018 , 186 1 ): 111 -152
DOI:10.1007/s00605-017-1019-0
PMID:31258193
[本文引用: 1]
We develop a theory of -matrix Riemann-Hilbert problems for a class of jump contours and jump matrices of low regularity. Our basic assumption is that the contour is a finite union of simple closed Carleson curves in the Riemann sphere. In particular, unbounded contours with cusps, corners, and nontransversal intersections are allowed. We introduce a notion of -Riemann-Hilbert problem and establish basic uniqueness results and Fredholm properties. We also investigate the implications of Fredholmness for the unique solvability and prove a theorem on contour deformation.
[44]
Its A R . Asymptotics of solutions of the nonlinear Schrödinger equation and isomonodromic deformations of systems of linear differential equations
Dokl akad nauk Sssr , 1981 , 24 452 -456
[本文引用: 1]
[45]
Zakharov V E Ostrovsky L A . Modulation instability: the beginning
Physica D , 2009 , 238 540 -548
DOI:10.1016/j.physd.2008.12.002
URL
Stability of periodic waves of finite amplitudeon the surfaceof a deepfluid
1
1968
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
1
1995
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
Comparisons between sine-Gordon and perturbed nonlinear Schr?dinger equations for modeling light bullets beyond critical collapse
1
2010
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
1
1995
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
1
1997
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
1
2003
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
Computational methods for the dynamics of the nonlinear Schr?dinger/Gross-Pitaevskii equations
1
2013
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
Financial rogue waves
1
2010
... 在数学物理领域有着重要的意义, 并且广泛应用于描述非线性波现象,如深海[1 ] ,非线性光学[2 -3 ] ,大气[4 ] ,等离子体[5 ] ,玻色-爱因斯坦凝聚[6 -7 ] ,甚至金融学[8 ] 等. 然而, 为了描述高阶非线性效应在实际数学和物理系统中的贡献, 在 NLS 方程(1.1)中添加高阶非线性项是不可避免的. 高阶非线性项不仅可以扩展克尔型非线性的范畴,而且改变了输入场强对无线端脉冲宽度的 NLS 方程NLS的影响.因此, 对广义 NLS 方程进行研究是必要也是值得的. 本文主要研究了聚焦 Kundu-Eckhaus (KE) 方程 ...
Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schr?dinger-type equations
1
1984
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Darboux transformations for a Lax integrable system in $2n$ -dimensions
1
1997
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
1
1991
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Soliton solutions by Darboux transformation and some reductions for a new Hamiltonian lattice hierarchy
1
2010
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Darboux transformation and soliton solutions for generalized nonlinear Schr?dinger equations
1
1999
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
The rogue waves with quintic nonlinearity and nonlinear dispersion effects in nonlinear optical fibers
1
2015
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Higher-order rogue wave solutions of the Kundu-Eckhaus equation
1
2014
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Inverse scattering method for the Kundu-Eckhaus equation with zero/nonzero boundary conditions
1
2021
... 该方程是由 Kundu[9 ] 提出, 其中 $\beta$ $\beta^{2}$ $\beta=0$ [10 ⇓ -12 ] ,聚焦 KE 方程是一个具有 Lax 对、孤子解和怪波解的完全可积系统[13 ⇓ -15 ] .在适当的条件下对方程(1.2)应用反散射变换法,使得产生各种与物理应用[16 ] 相关的解成为可能. ...
Solitons and the Inverse Scattering Transform
1
1981
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Inverse scattering transform for the nonlocal reverse space-time nonlinear Schr?dinger equation
1
2018
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Method for solving the Korteweg-de Vries equation
1
1967
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Inverse scattering transforms and soliton solutions of nonlocal reverse-space nonlinear Schr?dinger hierarchies
1
2020
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
A steepest descent method for oscillatory Riemann-Hilbert problems
4
1993
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 非线性可积系统柯西问题的解可以通过构造并求解相关 Riemann-Hilbert 问题来表示, 这使得非线性速降法能够更好地分析解的长时间渐进性. 据我们所知, 该方法最初是针对初边值条件为零的情况[21 ] 提出的. 为了解决非零初边值的问题, 出现了所谓的 $g$ [22 ] , 它与跳跃矩阵的某些项随着 $t$
... 根据文献[21 ], 通过对基本的 Riemann-Hilbert 问题变形可得到一个新的可解的 Riemann-Hilbert 问题. ...
... 通过将 $n^{(2)}$ [21 ] 进行对比, 发现唯一差异是近似中的一个只与 $\xi$ $p(\lambda)$ . ...
The collisionless shock region for the long-time behavior of solutions of the KdV equation
2
1994
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 非线性可积系统柯西问题的解可以通过构造并求解相关 Riemann-Hilbert 问题来表示, 这使得非线性速降法能够更好地分析解的长时间渐进性. 据我们所知, 该方法最初是针对初边值条件为零的情况[21 ] 提出的. 为了解决非零初边值的问题, 出现了所谓的 $g$ [22 ] , 它与跳跃矩阵的某些项随着 $t$
The focusing NLS equation with step-like oscillating background: scenarios of long-time asymptotics
2
2021
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 证 具体证明可参考文献[23 ]. ...
The focusing NLS equation with step-like oscillating background: the genus 3 sector
1
2022
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Focusing NLS equation: long-time dynamics of step-like initial data
2
2011
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 参考 Riemann-Hilbert 问题在文献[25 ]中进一步变形的过程. ...
Long-time asymptotics for the focusing NLS equation with time-periodic boundary condition on the half-line
1
2009
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Long-time asymptotics of the nonlinear Schr?dinger equation Shock problem
2
2007
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 根据文献[27 ,28 ], 可得两个修正的 Riemann-Hilbert 问题的解 $n^{mod_{-j}}$ $j=1,2$ . ...
Long-time asymptotics for the focusing nonlinear Schr?dinger equation with nonzero boundary conditions at infinity and asymptotic stage of modulational instability
2
2017
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
... 根据文献[27 ,28 ], 可得两个修正的 Riemann-Hilbert 问题的解 $n^{mod_{-j}}$ $j=1,2$ . ...
The integrable nature of modulational instability
1
2015
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Universal nature of the nonlinear stage of modulational instability
1
2016
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Long-time asymptotic for the derivative nonlinear Schr?dinger equation with step-like initial value
1
2013
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Long-time asymptotics for the defocusing integrable discrete nonlinear Schr?dinger equation
1
2014
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
The nonlinear steepest descent method: asymptotics for initial-boundary value problems
1
2016
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Asymptotic stage of modulation instability for the nonlocal nonlinear Schr?dinger equation
1
2021
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schr?dinger equation with time-periodic boundary condition
1
2018
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
Long-time behavior for the Cauchy problem of the 3-component Manakov system
1
2020
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
The nonlinear steepest descent approach for long time behavior of the two-component coupled Sasa-Satsuma equation with a $5\times5$ Lax pair
1
2021
... 反散射变换法是二十世纪数学的一项重要成就[17 ⇓ ⇓ -20 ] ,在无反射势情况下得到了许多非线性可积方程初值问题的精确解. 然而, 对于一般的初边值问题,并不能求解出显式解. 故针对非线性可积模型解的长时间渐近性的研究变得非常有意义. 近年来, 这一课题取得了许多进展,尤其是用于求解振荡 Riemann-Hilbert 问题的非线性速降法[21 -22 ] . 基于该方法, 关于 NLS 方程(1.1)初边值问题解的长时间渐近性方面的研究成果[23 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -34 ] 逐渐发展且丰富起来. 同时也涌现了对于具有多分量谱问题的非线性可积系统的相关研究[35 ⇓ -37 ] . ...
A Riemann-Hilbert approach to a generalized nonlinear Schr?dinger equation on the quarter plane
2
2020
... 虽然现已存在 KE 方程解的长时间渐进性的一些工作[38 ⇓ ⇓ -41 ] , 但大都关于初边值条件为零或简单非零边值条件的情况. 因此, 本文利用非线性速降法探索在阶跃振荡背景下聚焦 KE 方程(1.2)解的长时间渐进性. 当 $x\rightarrow\pm\infty$
... 现已存在情况(1)的相关研究[38 ⇓ ⇓ -41 ] , 故在这里重点探讨另一种情况. ...
Long-time asymptotics for the Kundu-Eckhaus equation on the half-line
2
2018
... 虽然现已存在 KE 方程解的长时间渐进性的一些工作[38 ⇓ ⇓ -41 ] , 但大都关于初边值条件为零或简单非零边值条件的情况. 因此, 本文利用非线性速降法探索在阶跃振荡背景下聚焦 KE 方程(1.2)解的长时间渐进性. 当 $x\rightarrow\pm\infty$
... 现已存在情况(1)的相关研究[38 ⇓ ⇓ -41 ] , 故在这里重点探讨另一种情况. ...
Long-time asymptotics and the bright $N$ -soliton solutions of the Kundu-Eckhaus equation via the Riemann-Hilbert approach
2
2018
... 虽然现已存在 KE 方程解的长时间渐进性的一些工作[38 ⇓ ⇓ -41 ] , 但大都关于初边值条件为零或简单非零边值条件的情况. 因此, 本文利用非线性速降法探索在阶跃振荡背景下聚焦 KE 方程(1.2)解的长时间渐进性. 当 $x\rightarrow\pm\infty$
... 现已存在情况(1)的相关研究[38 ⇓ ⇓ -41 ] , 故在这里重点探讨另一种情况. ...
Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions
2
2019
... 虽然现已存在 KE 方程解的长时间渐进性的一些工作[38 ⇓ ⇓ -41 ] , 但大都关于初边值条件为零或简单非零边值条件的情况. 因此, 本文利用非线性速降法探索在阶跃振荡背景下聚焦 KE 方程(1.2)解的长时间渐进性. 当 $x\rightarrow\pm\infty$
... 现已存在情况(1)的相关研究[38 ⇓ ⇓ -41 ] , 故在这里重点探讨另一种情况. ...
The nonlinear steepest descent method for Riemann-Hilbert problems of low regularity
2
2017
... 在 $L^{2}$ - 范数[42 ,43 ] 意义下, 定义 Riemann-Hilbert 问题 ...
... 进而, 对于 $\lambda\in{\Bbb C}\setminus\tilde{\Gamma}$ $(\hat{{\cal C}}f)(\lambda)=\frac{1}{2\pi {\rm i}}\int_{\tilde{\Gamma}}\frac{f(k)}{k-\lambda}{\rm d}k$ $\tilde{\Gamma}$ $\hat{{\cal C}}_{\pm}f$ . 根据文献[42 ]可知柯西算子的定义 $\hat{{\cal C}}_{\hat{\omega}}: L^{2}(\tilde{\Gamma})\rightarrow L^{2}(\tilde{\Gamma})$ $\hat{{\cal C}}_{\hat{\omega}}f = \hat{{\cal C}}_{-}(f\hat{\omega})$ . ...
Matrix Riemann-Hilbert problems with jumps across Carleson contours
1
2018
... 在 $L^{2}$ - 范数[42 ,43 ] 意义下, 定义 Riemann-Hilbert 问题 ...
Asymptotics of solutions of the nonlinear Schr?dinger equation and isomonodromic deformations of systems of linear differential equations
1
1981
... 根据抛物线柱面函数[44 ]}, 可知 Riemann-Hilbert 问题(4.35)有显式解. ...
Modulation instability: the beginning
0
2009