聚焦 Kundu-Eckhaus 方程的反散射变换法: 阶跃振荡背景下的长时间渐进性

摘要/Abstract

摘要：

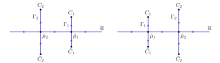
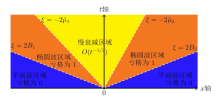
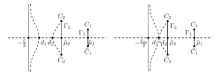
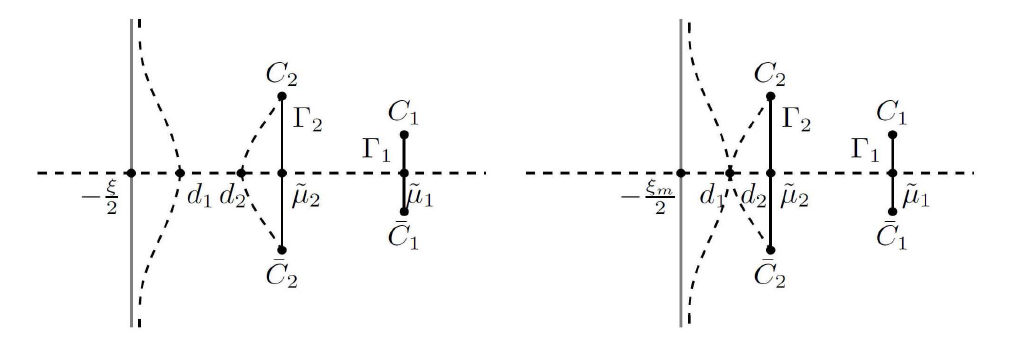
该文利用非线性速降法研究了阶跃振荡背景下聚焦 Kundu-Eckhaus 方程解的长时间渐进性问题. 在稀疏情况下, 当解趋于 $x$ 轴时, 其渐进性以平面波的形式呈现;当解趋于 $t$ 轴时, 其渐进性以缓慢衰减的形式呈现; 而在两个过渡扇区, 解的渐进性可表示为调制椭圆波函数. 此外, 在激波情况下, 解的渐进性可由依赖于亏格为3的黎曼曲面的超椭圆函数表示.该文所得结论有助于解释存在五次非线性项以及自频移效应的调制不稳定性下的非线性阶段.

关键词: 聚焦 Kundu-Eckhaus 方程, 反散射变换法, Riemann-Hilbert 问题, 非线性速降法

Abstract:

In this paper, we study the long-time dynamics of the solution of the focusing Kundu-Eckhaus equation under steplike oscillating background via the nonlinear steepest descent method. In the rarefaction case, when the solution is near the $x$-axis, the form of the leading behavior is the plane waves, when the solution tends to the $t$-axis, the leading behavior decays slowly, and when the solution belongs to two transition sectors, the form of the leading behavior is the elliptic waves. Furthermore, in the shock case, the leading behavior is described by terms of hyperelliptic functions depended on a Riemann surface of genus 3. Our results may be useful to explain the nonlinear stage of modulation instability in presence of the the quintic nonlinear and the self-frequency shift effects.

Key words: The focusing Kundu-Eckhaus equation, Inverse scattering transform, Riemann-Hilbert problem, The nonlinear steepest descent method

中图分类号:

O175.2

王贵贤,王秀彬,韩波. 聚焦 Kundu-Eckhaus 方程的反散射变换法: 阶跃振荡背景下的长时间渐进性[J]. 数学物理学报, 2023, 43(4): 1085-1122.

Wang Guixian,Wang XiuBin,Han Bo. Inverse Scattering Transform for the Focusing Kundu-Eckhaus Equation: Long-time Dynamics of the Steplike Oscillating Background[J]. Acta mathematica scientia,Series A, 2023, 43(4): 1085-1122.

图/表 14

图2.1

图3.1

图3.2

图3.3

图3.4

图4.1

图4.2

图4.3

图4.4

图4.5

图4.6

图4.7

图4.8

图4.9

参考文献 45

[1]	Zakharov V E. Stability of periodic waves of finite amplitudeon the surfaceof a deepfluid. J Appl Mech Tech Phys, 1968, 9: 190-194 doi: 10.1007/BF00913182
[2]	Agrawal G P. Nonlinear Fiber Optics. New York: Academic Press, 1995
[3]	Bao W Z, Dong X C, Xin J. Comparisons between sine-Gordon and perturbed nonlinear Schrödinger equations for modeling light bullets beyond critical collapse. Physica D, 2010, 239: 1120-1134 doi: 10.1016/j.physd.2010.03.002
[4]	Hasegawa A, Kodama Y. Solitons in Optical Communications. Oxford: Oxford University Press, 1995
[5]	Akhmediev N, Ankiewicz A. Solitons: Nonlinear Pulses and Beams. London: Chapmanand Hall, 1997
[6]	Pitaevskii L, Stringari S. Bose-Einstein Condensation. Oxford: Oxford University Press, 2003
[7]	Antoine X, Bao W Z, Besse C. Computational methods for the dynamics of the nonlinear Schrödinger/Gross-Pitaevskii equations. Computer Physics Communications, 2013, 184: 2621-2633 doi: 10.1016/j.cpc.2013.07.012
[8]	Yan Z. Financial rogue waves. Commun Theor Phys, 2010, 54: 947-949 doi: 10.1088/0253-6102/54/5/31
[9]	Kundu A. Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations. J Math Phys, 1984, 25: 3433 doi: 10.1063/1.526113
[10]	Ma W X. Darboux transformations for a Lax integrable system in $2n$-dimensions. Lett Math Phys, 1997, 39: 33-49 doi: 10.1007/s11005-997-3049-3
[11]	Matveev V B, Salle M A. Darboux Transformations and Solitons. Berlin: Springer, 1991
[12]	Tian S F, Zhang H Q. Soliton solutions by Darboux transformation and some reductions for a new Hamiltonian lattice hierarchy. Phys Scr, 2010, 82: 015008 doi: 10.1088/0031-8949/82/01/015008
[13]	Geng X G, Tam H W. Darboux transformation and soliton solutions for generalized nonlinear Schrödinger equations. J Phys Soc Jpn, 1999, 68: 1508 doi: 10.1143/JPSJ.68.1508
[14]	Zhao L C, Liu C, Yang Z Y. The rogue waves with quintic nonlinearity and nonlinear dispersion effects in nonlinear optical fibers. Commun Nonlinear Sci Numer Simul, 2015, 20: 9-13 doi: 10.1016/j.cnsns.2014.04.002
[15]	Wang X, Yang B, Chen Y, Yang Y Q. Higher-order rogue wave solutions of the Kundu-Eckhaus equation. Phys Scr, 2014, 89: 095210 doi: 10.1088/0031-8949/89/9/095210
[16]	Wang G X, Wang X B, Han B, Xue Q. Inverse scattering method for the Kundu-Eckhaus equation with zero/nonzero boundary conditions. Z Naturforsch A, 2021, 76(4): 315-327 doi: 10.1515/zna-2020-0327
[17]	Ablowitz M J, Segur H. Solitons and the Inverse Scattering Transform. Philadelphia: SIAM, 1981
[18]	Ablowitz M J, Feng B F, Luo X D, Musslimani Z H. Inverse scattering transform for the nonlocal reverse space-time nonlinear Schrödinger equation. Theor Math Phys, 2018, 196(3): 1241-1267 doi: 10.1134/S0040577918090015
[19]	Gardner C S, Greene J M, Kruskal M D, Miura R M. Method for solving the Korteweg-de Vries equation. Phys Rev Lett, 1967, 19: 1095-1097 doi: 10.1103/PhysRevLett.19.1095
[20]	Ma W X, Huang Y H, Wang F D. Inverse scattering transforms and soliton solutions of nonlocal reverse-space nonlinear Schrödinger hierarchies. Stud Appl Math, 2020, 145: 563-585 doi: 10.1111/sapm.v145.3
[21]	Deift P, Zhou X. A steepest descent method for oscillatory Riemann-Hilbert problems. Ann Math, 1993, 137(2): 295-368 doi: 10.2307/2946540
[22]	Deift P, Venakides S, Zhou X. The collisionless shock region for the long-time behavior of solutions of the KdV equation. Commun Pure Appl Math, 1994, 47(2): 199-206 doi: 10.1002/(ISSN)1097-0312
[23]	De Monvel A B, Lenells J, Shepelsky D. The focusing NLS equation with step-like oscillating background: scenarios of long-time asymptotics. Commun Math Phys, 2021, 383: 893-952 doi: 10.1007/s00220-021-03946-x
[24]	De Monvel A B, Lenells J, Shepelsky D. The focusing NLS equation with step-like oscillating background: the genus 3 sector. Commun Math Phys, 2022, 390(3): 1081-1148 doi: 10.1007/s00220-021-04288-4
[25]	De Monvel A B, Kotlyarov V P, Shepelsky D. Focusing NLS equation: long-time dynamics of step-like initial data. Int Math Res Not, 2011, 7: 1613-1653
[26]	De Monvel A B, Its A, Kotlyarov V. Long-time asymptotics for the focusing NLS equation with time-periodic boundary condition on the half-line. Comm Math Phys, 2009, 290: 479-522 doi: 10.1007/s00220-009-0848-7
[27]	Buckingham R, Venakides S. Long-time asymptotics of the nonlinear Schrödinger equation Shock problem. Comm Pure Appl Math, 2007, 60(9): 1349-1414 doi: 10.1002/(ISSN)1097-0312
[28]	Biondini G, Mantzavinos D. Long-time asymptotics for the focusing nonlinear Schrödinger equation with nonzero boundary conditions at infinity and asymptotic stage of modulational instability. Comm Pure Appl Math, 2017, 70(12): 2300-2365 doi: 10.1002/cpa.v70.12
[29]	Biondini G, Fagerstrom E. The integrable nature of modulational instability. SIAM J Appl Math, 2015, 75: 136-163 doi: 10.1137/140965089
[30]	Biondini G, Mantzavinos D. Universal nature of the nonlinear stage of modulational instability. Phys Rev Lett, 2016, 116(4): 043902 doi: 10.1103/PhysRevLett.116.043902
[31]	Xu J, Fan E G, Chen Y. Long-time asymptotic for the derivative nonlinear Schrödinger equation with step-like initial value. Math Phys Anal Geom, 2013, 16: 253-288 doi: 10.1007/s11040-013-9132-3
[32]	Yamane H. Long-time asymptotics for the defocusing integrable discrete nonlinear Schrödinger equation. J Math Soc Jpn, 2014, 6: 765-803
[33]	Lenells J. The nonlinear steepest descent method: asymptotics for initial-boundary value problems. SIAM J Math Anal, 2016, 48: 2076-2118 doi: 10.1137/15M1036889
[34]	Rybalko Y, Shepelsky D. Asymptotic stage of modulation instability for the nonlocal nonlinear Schrödinger equation. Physica D, 2021, 428: 133060 doi: 10.1016/j.physd.2021.133060
[35]	Tian S F, Zhang T T. Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schrödinger equation with time-periodic boundary condition. P Am Math Soc, 2018, 146(4): 1713-1729
[36]	Wang X B, Han B. Long-time behavior for the Cauchy problem of the 3-component Manakov system. Phys Scr, 2020, 95: 065226 doi: 10.1088/1402-4896/ab85ff
[37]	Wang X B, Han B. The nonlinear steepest descent approach for long time behavior of the two-component coupled Sasa-Satsuma equation with a $5\times5$ Lax pair. Taiwanese J Math, 2021, 25(2): 381-407
[38]	Wang X B, Han B. A Riemann-Hilbert approach to a generalized nonlinear Schrödinger equation on the quarter plane. Math Phys Anal Geom, 2020, 23: 25 doi: 10.1007/s11040-020-09347-1
[39]	Guo B L, Nan L. Long-time asymptotics for the Kundu-Eckhaus equation on the half-line. J Math Phys, 2018, 59: 061505 doi: 10.1063/1.5020996
[40]	Wang D S, Wang X L. Long-time asymptotics and the bright $N$-soliton solutions of the Kundu-Eckhaus equation via the Riemann-Hilbert approach. Nonlinear Anal Real World Appl, 2018, 41: 334-361 doi: 10.1016/j.nonrwa.2017.10.014
[41]	Wang D S, Guo B L, Wang X L. Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions. J Differential Equations, 2019, 266: 5209-5253 doi: 10.1016/j.jde.2018.10.053
[42]	Lenells J. The nonlinear steepest descent method for Riemann-Hilbert problems of low regularity. Indiana Math J, 2017, 66(4): 1287-1332 doi: 10.1512/iumj.2017.66.6078
[43]	Lenells J. Matrix Riemann-Hilbert problems with jumps across Carleson contours. Monatsh Math, 2018, 186(1): 111-152 doi: 10.1007/s00605-017-1019-0 pmid: 31258193
[44]	Its A R. Asymptotics of solutions of the nonlinear Schrödinger equation and isomonodromic deformations of systems of linear differential equations. Dokl akad nauk Sssr, 1981, 24: 452-456
[45]	Zakharov V E, Ostrovsky L A. Modulation instability: the beginning. Physica D, 2009, 238: 540-548 doi: 10.1016/j.physd.2008.12.002