1 引言
近年来, 随着金融市场的快速发展和人口老龄化的趋势不断加强, 养老保险制度在当今生活中发挥着越来越重要的作用. 目前, 确定缴费(DC)型养老金计划和确定收益(DB)型养老金计划是养老保险制度的两种主要表现形式. 由于DC型养老金计划的投资风险和长寿风险是由养老金参与者本身承担, 这比较符合当前的养老金管理机制. 同时, 许多国家都采用了DC型养老金计划. 因此, DC型养老金计划比DB型养老金计划在养老保险制度中更加受欢迎. 近年来, DC型养老金计划的最优投资和管理问题得到了金融界和保险界的广泛研究.
DC型养老金计划在资金积累阶段的投资管理问题主要集中在两种研究目标上. 第一种目标是最大化DC型养老金计划终端财富的期望效用. Guan和Liang[8]讨论了具有随机波动率风险和随机利率风险的DC型养老金预期CRRA效用最大化问题. Mudzimbabwe[20] 用跳跃扩散模型描述风险资产, 最大化DC型养老金终端财富的预期指数效用. 第二种目标是在均值-方差准则下研究DC 型养老金计划终端财富期望最大化和方差最小化问题. 目前, 有大量的文献研究了Markowitz[19]提出的均值-方差投资组合问题. Li和Ng[14]和Zhou和Li[27]运用嵌入技术, 将均值-方差问题转化为随机线性二次控制问题, 得到了一个预承诺投资策略. 在多期均值-方差框架下, Yao等[25]讨论了具有死亡风险和随机工资的养老金计划的最优投资问题. Guan和Liang[9] 提出了均值回复股价模型, 考虑了具有随机利率的DC型养老金的均值-方差优化问题.
然而, 上述文献忽略了均值-方差优化问题的时间不一致性. 由于均值-方差目标函数中的方差项是关于期望的非线性函数, 它不满足迭代期望性质, Bellman 最优性原理不再成立. 因此, 均值-方差优化问题是时间不一致的. 上述文献中的预承诺策略是全局最优但时间不一致的投资策略, 即它在初始时刻是最优的, 在未来时刻它不一定仍然是最优的. 由于DC 型养老金计划的投资期限较长, 养老金管理者的偏好会随着时间的变化而发生改变, 因此他们更倾向于寻找一个时间一致的投资策略. 在博弈论框架内, Björk和Murgoci[2]研究了一般的马尔可夫时间不一致随机控制问题, 寻求一个子博弈完美那什均衡投资策略. 随后, 许多学者在此基础上, 通过求解扩展的HJB方程系统, 得到了均值-方差问题的均衡投资策略(即时间一致性投资策略). 因此, 在DC型养老金的投资问题中, 均衡策略已经成为处理时间不一致性问题的主要方法. 在均值-方差框架下, Li 等[15]考虑了具有违约风险和保费退还条款的DC型养老金计划. Wang等[24]研究了部分信息下的DC型养老金的均衡投资策略.
在金融市场中, 错误定价现象是普遍存在的. 错误定价是指同一资产在不同的金融市场上具有不同的交易价格. 一些中国公司(例如中国银行和中国农业银行等)的股票在中国证券交易所(例如上海和深圳等)和香港证券交易所分别作为A 股和H股交易, 同时这两支股票的交易价格存在显著差异. 2015年, 中国政府开放了对中国大陆和香港金融市场的同步投资, 这意味着中国个人投资者可以在中国大陆和香港金融市场上同时进行股票交易. 因此, 在这种情况下, 一些投资者可以利用两个市场中的A 股和H股之间的价格差异, 通过做空定价过高的股票并且购买相同数量定价过低的股票来获得套利机会. Gu等[6-7]考虑了具有错误定价和模糊厌恶的保险公司的最优比例再保险投资问题. Gu等[6]进一步研究了具有错误定价和均值回归模型的保险公司的最优稳健再保险投资策略. 此外, Wang等[21]和Wang等[23]也都考虑了具有错误定价保险公司的投资问题. 上述研究都涉及到保险和再保险投资问题. 还有一些文献考虑错误定价下的DC型养老金问题. 在CRRA 效用函数下, Ma 等[18]考虑了遵循 Heston 模型的风险资产价格过程, 研究了存在错误定价的DC 型养老金的资产配置问题. Liu等[17]在HARA效用函数下讨论了存在错误定价的DC 型养老金的最优投资问题. 受上述文献的启发, 我们的目标是在均值-方差准则下, 为存在错误定价的DC型养老金导出时间一致的均衡投资策略.
由于Heston[11]提出的Heston模型在Feller条件下几乎是处处非负的, 因此它在资产配置和衍生品定价的文献中广受欢迎. 然而, 当Heston模型被校准到真实数据时, Feller条件往往是不满足的. Heston[12]提出了进一步克服Heston模型的局限性的
本文在均值-方差框架下, 引入了
本文剩余研究内容如下. 在第2节中, 我们介绍了一些金融市场中的资产模型公式, 引入了保费返还条款, 得到了财富过程的表达式. 在第3节中, 我们得到了均值-方差优化问题的均衡投资策略以及相应的均衡有效前沿的表达式. 在第4节中, 我们对一些数值模拟结果进行了分析. 第5节是全文内容的总结.
2 金融市场
定义
假设金融市场上存在三种可连续进行交易的资产: 无风险资产(即现金或银行账户), 市场指数和一对错误定价的股票. 无风险资产
其中, 常数
市场指数
其中,
当
我们定义定价误差
其中,
其中,
因此, 根据Itô公式, 我们可以得到定价误差
在DC型养老金计划中, 养老金参与者在资金累积期间需要对养老金账户进行连续的缴费. 假设养老金参与者在单位时间内的缴费金额是预先确定的, 记为常数
其中
定义
以及
其中,
因此, (2.8)式可以写成
当
我们引入Abraham De Moivre 模型(Kohler和Kohler[13])中的死亡力函数
其中,
其中,
(1)
(2)
(3) 对于任意的
此外, 我们这里定义DC型养老金计划的所有容许策略构成的集合为
3 最优投资策略
在这一部分, 我们考虑一个DC型养老金在均值-方差准则下的投资问题. DC型养老金管理者的目标是最大化终端财富的期望, 同时最小化终端财富的方差, 使得养老金账户在退休时的财富金额达到最高且投资风险达到最低. 假设养老金的终端财富为
其中,
在优化问题(3.1)中,
其中,
如果有下式成立
则称
定义3.1给出的均衡策略是时间一致的. 我们的目标是求解均值-方差优化问题(3.1), 并且找到均衡投资策略和相应的均衡值函数. 下面, 我们将均值- 方差优化问题(3.1)的目标函数定义为
其中,
对于任意的
其中,
其中, 对于任意的
分别定义
其中,
在求解具有
以及
其中, 边界条件为
以及
其中,
另外, 我们还可以得到
以及
由定理3.1知,
同时, 相应的均衡值函数
以及在均衡策略
其中
其中, 它们的边界条件为
接下来, 我们分别对(3.24)式和(3.25)式关于
将上述各项偏导代入到(3.6)式和(3.7)式中, 可以得到
以及
根据一阶最优条件, 对(3.26)式分别关于
将(3.28)式代入到(3.26)式和(3.27)式, 可以得到
以及
分别分离(3.29)式和(3.30)式变量, 并且结合边界条件, 我们可以得到如下方程
通过求解(3.31)-(3.40)式, 我们可以得到(3.16)-(3.23) 式, 从而得到了
其中
因此, 由(3.41)式, 我们有
从而有
特别地, 在时间
4 数据分析
在本节中, 我们将通过一些数值算例来展示风险厌恶系数, 错误定价和保费退还条款对上文中得到的均衡投资策略和相应的均衡有效前沿的影响. 除非另有说明, 模型的相关参数值设置为: T=40,~w=100,~w_{0}=20,~c=1,~r=0.05, \lambda=2.9428, c_{1}=0.9051, c_{2}=0.0023, k=7.3479,~\theta_{v}=0.0328,~\sigma_{v}=0.6612, \rho=-0.7689,~\beta=1.1,~\sigma=0.3, b=0.3,~l_{1}=0.1, l_{2}=0.2, x_{0}=1,~v_{0}=0.02,~m_{0}=0.04,~\gamma=0.8.
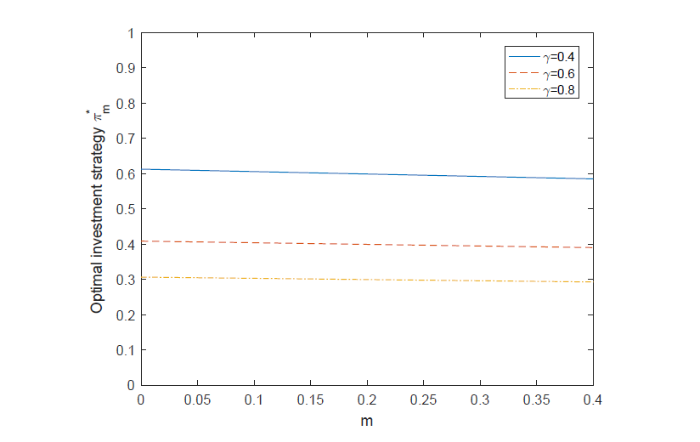
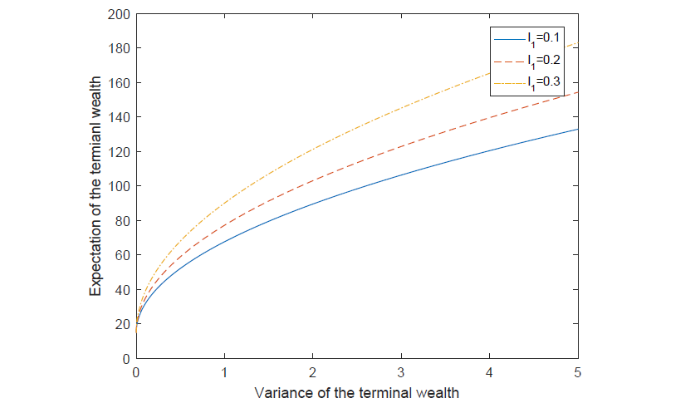
图1表明了风险厌恶系数
图 1
图 2
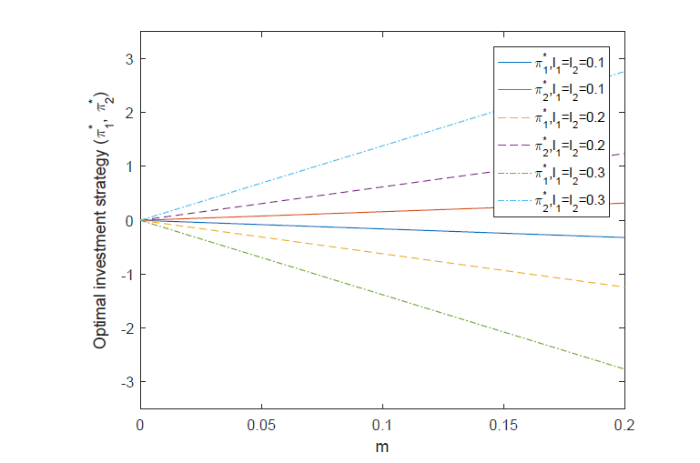
图3表明了当
图 3
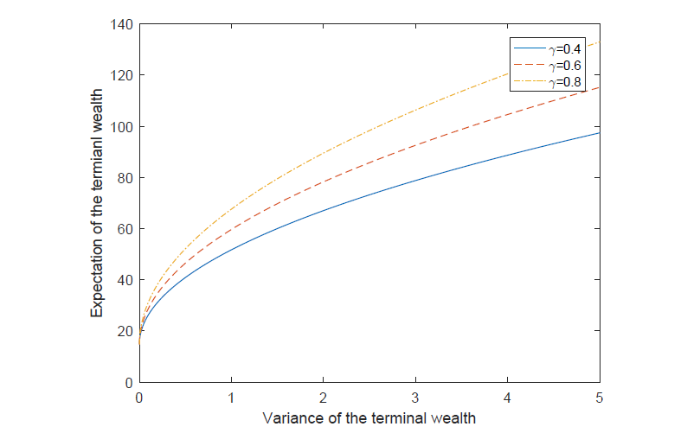
图4表明了风险厌恶系数
图 4
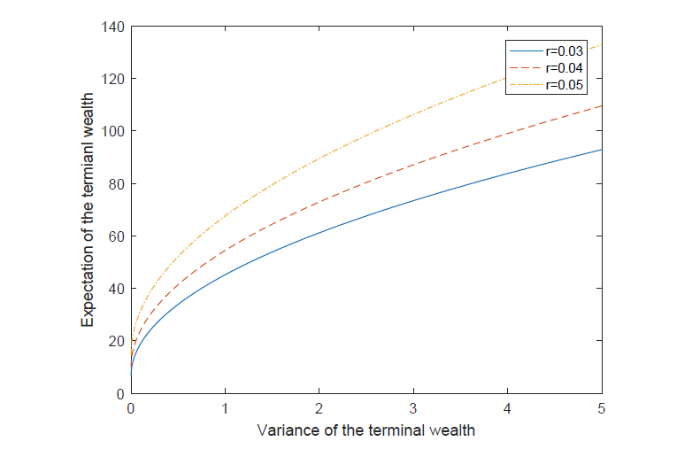
图5表明了无风险利率
图 5
图6表明了参数
图 6
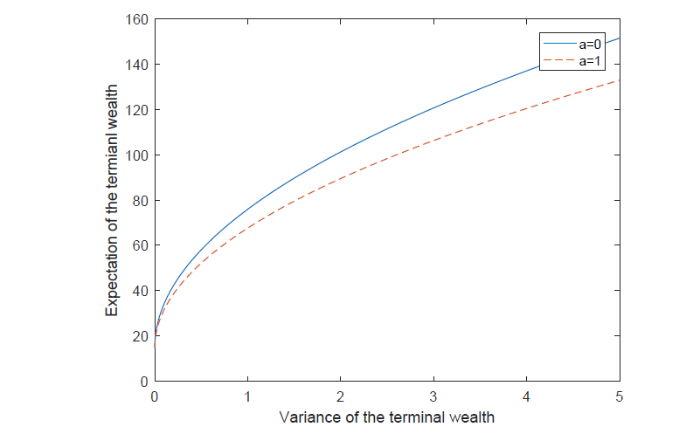
图7表明了保费退还条款对均衡有效前沿的影响, 考虑保费退还条款(即
图 7
5 结论
本文在DC型养老金计划的均衡投资问题中引入了
参考文献
Pre-commitment and equilibrium investment strategies for the DC pension plan with regime switching and a return of premiums clause
DOI:10.1016/j.insmatheco.2018.05.005 URL [本文引用: 1]
A general theory of Markovian time inconsistent stochastic control problems
Robust equilibrium strategy for DC pension plan with the return of premiums clauses in a jump-diffusion model
Optimal investment strategy in the family of
DOI:10.1080/14697688.2020.1825781 URL [本文引用: 1]
The
DOI:10.1111/mafi.2017.27.issue-4 URL [本文引用: 2]
Optimal robust reinsurance-investment strategies for insurers with mean reversion and mispricing
DOI:10.1016/j.insmatheco.2018.03.004 URL [本文引用: 2]
Optimal reinsurance and investment strategies for insurers with mispricing and model ambiguity
DOI:10.1016/j.insmatheco.2016.11.007 URL [本文引用: 1]
Optimal management of DC pension plan in a stochastic interest rate and stochastic volatility framework
DOI:10.1016/j.insmatheco.2014.05.004 URL [本文引用: 1]
Mean-variance efficiency of DC pension plan under stochastic interest rate and mean-reverting returns
DOI:10.1016/j.insmatheco.2014.12.006 URL [本文引用: 1]
Optimal investment strategy for the DC plan with the return of premiums clauses in a mean-variance framework
DOI:10.1016/j.insmatheco.2013.09.002 URL [本文引用: 2]
A closed-form solution for options with stochastic volatility with applications to bond and currency options
DOI:10.1093/rfs/6.2.327 URL [本文引用: 2]
A simple new formula for options with stochastic volatility
Frailty modeling for adult and old age mortality: the application of a modified De Moivre Hazard function to sex differentials in mortality
Optimal dynamic portfolio selection: Multi-period mean-variance formulation
DOI:10.1111/mafi.2000.10.issue-3 URL [本文引用: 1]
Equilibrium investment strategy for DC pension plan with default risk and return of premiums clauses under CEV model
DOI:10.1016/j.insmatheco.2016.10.007 URL [本文引用: 2]
Optimal convergence trade strategies
DOI:10.1093/rfs/hhs130 URL [本文引用: 1]
Optimal portfolios for the DC pension fund with mispricing under the HARA utility framework
DOI:10.3934/jimo.2021228 URL [本文引用: 2]
Optimal investment strategy for a DC pension plan with mispricing under the Heston model
DOI:10.1080/03610926.2019.1586938 URL [本文引用: 2]
A simple numerical solution for an optimal investment strategy for a DC pension plan in a jump diffusion model
DOI:10.1016/j.cam.2019.03.043
[本文引用: 1]

In this paper, we study an optimal investment strategy for a fund manager of a DC pension who wants to maximise the expected exponential utility of the terminal wealth in a market where the stock is a jump diffusion process. Using stochastic control theory, we derive a Hamilton-Jacobi-Bellman equation. Since the market is not complete, the optimal strategy cannot be found in closed as is done in most literature on DC pension plans. We characterise the optimal strategy as a solution of an integro-ordinary differential equation which can easily be solved by a simple numerical method. We investigate the impact of different jump parameters through numerical experiments using a familiar distribution of jumps. (C) 2019 Elsevier B.V.
Optimal reinsurance-investment policies for insurers with mispricing under mean-variance criterion
DOI:10.1080/03610926.2018.1532006 URL [本文引用: 1]
Optimal investment and reinsurance strategies under
Robust optimal insurance and investment strategies for the government and the insurance company under mispricing phenomenon
DOI:10.1080/03610926.2019.1646765 URL [本文引用: 1]
Equilibrium investment strategy for a DC pension plan with learning about stock return predictability
DOI:10.1016/j.insmatheco.2021.07.001 URL [本文引用: 1]
Asset allocation for a DC pension fund with stochastic income and mortality risk: a multi-period mean-variance framework
DOI:10.1016/j.insmatheco.2013.10.016 URL [本文引用: 1]
Dynamic optimal mean-variance investment with mispricing in the family of
DOI:10.3390/math9182293
URL
[本文引用: 1]

This paper considers an optimal investment problem with mispricing in the family of 4/2 stochastic volatility models under mean–variance criterion. The financial market consists of a risk-free asset, a market index and a pair of mispriced stocks. By applying the linear–quadratic stochastic control theory and solving the corresponding Hamilton–Jacobi–Bellman equation, explicit expressions for the statically optimal (pre-commitment) strategy and the corresponding optimal value function are derived. Moreover, a necessary verification theorem was provided based on an assumption of the model parameters with the investment horizon. Due to the time-inconsistency under mean–variance criterion, we give a dynamic formulation of the problem and obtain the closed-form expression of the dynamically optimal (time-consistent) strategy. This strategy is shown to keep the wealth process strictly below the target (expected terminal wealth) before the terminal time. Results on the special case without mispricing are included. Finally, some numerical examples are given to illustrate the effects of model parameters on the efficient frontier and the difference between static and dynamic optimality.
Continuous-time mean-variance portfolio selection: A stochastic LQ framework
DOI:10.1007/s002450010003 URL [本文引用: 1]