1 引言
该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理.
本文的主要目标是应用L2格式和简单递归关系来求解分数阶微分方程, 包括由Caputo和Fabrizio提出的光滑核分数阶导数. Caputo-Fabrizio分数阶导数有助于理解一些现象, 如二级流体的热分析、电化学现象、异常扩散等.
(1.1) $\begin{equation}\label{1.1} {\cal D}_{t}^{\alpha}u(t)=f(t), \alpha\in (0,1), 0<t<T, \end{equation}$
初始条件$u(0)=u_{0}$ $f(t)=\lambda [u(t)-u_{0}\exp(-\frac{\alpha}{1-\alpha}t)],$ ${\cal D}_{t}^{\alpha}$
(1.2) $\begin{equation}\label{1.2} {\cal D}_{t}^{\alpha}u(t)=\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t}u'(\tau)\exp(-\alpha\frac{t-\tau}{1-\alpha}){\rm d}\tau, \end{equation}$
其中$\alpha\in(0,1)$ $M(\alpha)$ $M(0)=M(1)=1.$
结果表明, 当$u_{0}\lambda < 0$
该文的主要内容和结构如下: 在第2节中, 介绍了一些基本的定义; 在第3节中, 详细描述了Caputo-Fabrizio导数的算法; 第4节给出了解的存在性、误差估计和稳定性分析. 验证本文的理论结果的数值算例在第5节给出.
2 主要定义和概念
${\bf 定义 2.1}$ $\alpha$
(2.1) $\begin{equation}\label{2.1} D_{t}^{\alpha}u(t)=\frac{ 1}{\Gamma(1-\alpha)}\int_{a}^{t}\frac{u'(\tau)}{(t-\tau)^{\alpha}}{\rm d}\tau. \end{equation} $
${\bf 定义 2.2}$ $u\in H^{1}(a, b), b > a, \alpha\in[0,1]$
(2.2) $ \begin{equation}\label{2.2} {\cal D}_{t}^{\alpha}u(t)=\frac{ M(\alpha)}{1-\alpha}\int_{a}^{t}u'(\tau)\exp(-\alpha\frac{t-\tau}{1-\alpha}){\rm d}\tau, \end{equation}$
其中$\alpha \in(0,1)$ $M(\alpha)$ $M(0)=M(1)=1$ .
3 快速有限差分算子的构造
在该节中, 考虑方程(1.2)的高阶快速算法, 在区间$[T]$ $\Omega_{t}:=\{t_{n},$ $ n=0,1,\cdots, N\}$ $t_{0}=0, t_{N}=T,$ $h=\frac{T}{N}, t_{k-\frac{1}{2}}=t_{k-1}+\frac{1}{2}h, I_{k}=[t_{k-1}, t_{k}], $ $k=1,2,\cdots,N.$
它是一个二阶多项式, 在点$\{t_{j-1},t_{j},t_{j+1}\}$ $u(t)$ . 首先将(1.2)式中的卷积积分分为$D_{h}^{I}(t_{k})$ $D_{h}^{II}(t_{k})$
(3.1) $\begin{eqnarray*}\label{3.1} D_{h}^{I}(t_{k}) &\approx&\frac{M(\alpha)}{1-\alpha}\int_{t_{k-1}}^{t_{k}}[\prod_{2,k}u(\tau)]' \exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau\\ &=&a_{k,k-2}u(t_{k-2})+a_{k,k-1}u(t_{k-1})+a_{k,k}u(t_{k}), \end{eqnarray*}$
对于$D_{h}^{II}(t_{k})$ $u'(\tau)$
(3.2) $\begin{eqnarray*}\label{3.2} D_{h}^{II}(t_{k}) &=&\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{k-1}}u'(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau\\ &=&\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{k-1}}\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}u(\tau)\\ &=&\frac{ M(\alpha)}{1-\alpha}\bigg[u(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha})\bigg|_{0}^{t_{k-1}} -\int_{0}^{t_{k-1}}\frac{\alpha}{1-\alpha}u(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau\bigg]\\ &=&\frac{ M(\alpha)}{1-\alpha}\bigg[u(t_{k-1})\exp(\frac{-\alpha h}{1-\alpha})-u(0)\exp(\frac{-\alpha t_{k}}{1-\alpha})\\ &&-\frac{\alpha}{1-\alpha}\int_{0}^{t_{k-1}}u(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau\bigg]. \end{eqnarray*}$
对于$k=1,2,\cdots,N$ $H(t_{k})$
(3.3) $\begin{equation}\label{3.3} H(t_{k})=\exp(\frac{-\alpha h}{1-\alpha})H(t_{k-1})+ \int_{t_{k-2}}^{t_{k-1}}\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha})u(\tau){\rm d}\tau. \end{equation}$
在每一步, 只需要计算$H(t_{k})$ $H(t_{k-1})$ $u(t)$
(3.4) $\begin{equation}\label{3.4} D_{h}^{II}(t_{k})\approx\frac{ M(\alpha)}{1-\alpha} \bigg[u(t_{k-1})\exp(\frac{-\alpha h}{1-\alpha})-u(0)\exp(\frac{-\alpha t_{k}}{1-\alpha})-\frac{\alpha}{1-\alpha}H(t_{k})\bigg], \end{equation}$
下面本文引入有限差分算子$L_{h}^{\alpha}$ $\{u^{k}\}_{k=0}^{N}$ .
(3.5) $\begin{eqnarray*}\label{3.5} L_{h}^{\alpha}u_{k}&=&(a_{k,k-2}u_{k-2}+a_{k,k-1}u_{k-1}+a_{k,k}u_{k})\\ &&+\frac{ M(\alpha)}{1-\alpha}\bigg[\exp(\frac{-\alpha h}{1-\alpha})u_{k-1}-\exp(\frac{-\alpha t_{k}}{1-\alpha})u_{0}-\frac{\alpha}{1-\alpha}H(t_{k})\bigg]. \end{eqnarray*}$
当$k=1$ $I_{1}=[t_{0},t_{1}]$ $u(t)$
(3.6) $\begin{equation}\label{3.6} u(\tau)\approx\varphi_{1,0}(\tau)u_{0}+\varphi_{1,1}(\tau)u_{\frac{1}{2}}+\varphi_{1,2}(\tau)u_{1}, \end{equation}$
(3.7) $\begin{equation} \label{3.7} u_{\frac{1}{2}}\approx\frac{3}{8}u_{0}+\frac{3}{4}u_{1}-\frac{1}{8}u_{2}, \end{equation}$
(3.8) $\begin{eqnarray*}\label{3.8} u(\tau)&\approx&\bigg[\varphi_{1,0}(\tau)+\frac{3}{8}\varphi_{1,1}(\tau)\bigg]u_{0} +\bigg[\varphi_{1,2}(\tau)+\frac{3}{4}\varphi_{1,1}(\tau)\bigg]u_{1}-\frac{1}{8}\varphi_{1,1}(\tau)u_{2}\\ &\doteq&\omega_{0}(\tau)u_{0}+\omega_{1}(\tau)u_{1}+\omega_{2}(\tau)u_{2}, \end{eqnarray*}$
(3.9) $\begin{eqnarray*}\label{3.9} {\cal D}_{t}^{\alpha}u(t)|_{t=t_{1}} &=&\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\\ &\approx&\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}[\omega_{0}'(\tau)u_{0}+\omega_{1}'(\tau)u_{1}+\omega_{2}'(\tau)u_{2}]\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\\ &=&a_{1,0}u_{0}+a_{1,1}u_{1}+a_{1,2}u_{2}\\ &\doteq& L_{h}^{\alpha}u_{1}, k=1, \end{eqnarray*}$
(3.10) $ a_{1,i}=\frac{M(\alpha)}{1-\alpha}\int_{t_{0}}^{t_{1}}{\omega_{i}'(\tau)} \exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau, i=0,1,2. $
4 理论分析
(4.1) $\begin{equation}\label{4.1} b_{11}u_{1}+b_{12}u_{2}=-b_{10}u_{0}. \end{equation}$
其中 $ H(t_{2})=\hat{a}_{2,0}u_{0}+\hat{a}_{2,1}u_{1}+\hat{a}_{2,2}u_{2}, $
(4.2) $\begin{equation} b_{22}=a_{2,2}-\frac{\alpha M(\alpha)}{(1-\alpha)^{2}}\hat{a}_{2,2}-\lambda, \label{4.2} b_{21}u_{1}+b_{22}u_{2}=-b_{20}u_{0}. \end{equation} $
(4.3) $\begin{equation}\label{4.3} b_{31}u_{1}+b_{32}u_{2}+b_{33}u_{3}=-b_{30}u_{0}. \end{equation} $
同理, 可以得到$4\leq k\leq N$
(4.4) $\begin{eqnarray*} &&\bigg[-\frac{\alpha M(\alpha)}{(1-\alpha)^2}(\exp(\frac{ -(N-2)\alpha h}{1-\alpha})\hat{a}_{2,1}+\exp(\frac{ -(N-3)\alpha h}{1-\alpha})\hat{a}_{3,1})\bigg]u_{1}\\ &&+ \bigg[-\frac{\alpha M(\alpha)}{(1-\alpha)^2}(\exp(\frac{ -(N-2)\alpha h}{1-\alpha})\hat{a}_{2,2}+\exp(\frac{ -(N-3)\alpha h}{1-\alpha})\hat{a}_{3,2}+\exp(\frac{ -(N-4)\alpha h}{1-\alpha})\hat{a}_{4,2})\bigg]u_{2}\\ &&+ \bigg[-\frac{\alpha M(\alpha)}{(1-\alpha)^2}(\exp(\frac{ -(N-3)\alpha h}{1-\alpha})\hat{a}_{3,3}+\exp(\frac{ -(N-4)\alpha h}{1-\alpha})\hat{a}_{4,3})\bigg]u_{3}+\cdots \\ &&+ \bigg[a_{N,N-2}-\frac{\alpha M(\alpha)}{(1-\alpha)^2}(\exp(\frac{ -2\alpha h}{1-\alpha})\hat{a}_{N-2,N-2}+\exp(\frac{ -\alpha h}{1-\alpha})\hat{a}_{N-1,N-2}+\hat{a}_{N,N-2})\bigg]u_{N-2}\\ &&+ \bigg[a_{N,N-1}+\frac{M(\alpha)}{1-\alpha}\exp(\frac{ -\alpha h}{1-\alpha}-\frac{\alpha M(\alpha)}{(1-\alpha)^2}(\exp(\frac{ -\alpha h}{1-\alpha}\hat{a}_{N-1,N-1}+\hat{a}_{N,N-1})\bigg]u_{N-1}\\ &&+ \bigg[a_{N,N}-\frac{\alpha M(\alpha)}{(1-\alpha)^2}\hat{a}_{N,N}-\lambda\bigg]u_{N}\\ &=&-\bigg[\frac{ M(\alpha)}{(1-\alpha)}(-\exp(\frac{ -\alpha t_{N}}{1-\alpha}))-\frac{\alpha M(\alpha)}{(1-\alpha)^2}\exp (\frac{ -(N-2)\alpha h}{1-\alpha})\hat{a}_{2,0}+\exp(\frac{ -\alpha t_{N}}{1-\alpha})\bigg]u_{0},\label{4.4} \end{eqnarray*} $
(4.5) $\begin{equation}\label{4.5} \begin{array}{ll} b_{11}u_{1}+b_{12}u_{2}=\tilde{f}_{1}, b_{21}u_{1}+b_{22}u_{2}=\tilde{f}_{2},\\ b_{31}u_{1}+b_{32}u_{2}+b_{33}u_{3}=\tilde{f}_{3},\\ b_{41}u_{1}+b_{42}u_{2}+b_{43}u_{3}+b_{44}u_{4}=\tilde{f}_{4},\\ \cdots~~~~~~~\cdots~~~~~~~\cdots~~~~~~~\cdots~~~~~~~\cdots\\ b_{N-1 1}u_{1}+\cdots+b_{N-1 N-1}u_{N-1}=\tilde{f}_{N-1},\\ b_{N 1}u_{1}+b_{N 2}u_{2}+\cdots+b_{N N-1}u_{N-1}+b_{N N}u_{N}=\tilde{f}_{N}. \end{array} \end{equation} $
4.1 方程组(4.5)的可解性分析
接下来本文给出一些引理, 这些引理将用于可解性分析和稳定性分析.
${\bf 引理 4.1}$ $h<\frac{2(1-\alpha)}{\alpha}$
(4.6) $\begin{equation}\label{4.6} b_{11}b_{22}-b_{21}b_{12}> 0,~~\mbox{和} ~~b_{ii}>0, i=1,2,\cdots,N. \end{equation} $
${\bf证}$ $b_{11}$ $b_{kk}, 2\leq k\leq N,$
(4.7) $\begin{eqnarray*}\label{4.7} b_{kk} &=&a_{k,k}-\frac{\alpha M(\alpha)}{(1-\alpha)^2}\hat{a}_{k,k}-\lambda\\ &=&\frac{ M(\alpha)}{1-\alpha}\int_{t_{k-1}}^{t_{k}}\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\omega_{1}(\tau)-\lambda\\ &=&\frac{ M(\alpha)}{1-\alpha} \bigg[\omega_{1}(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha})\bigg|_{t_{k-1}}^{t_{k}} -\int_{t_{k-2}}^{t_{k-1}}\frac{\alpha}{1-\alpha}\varphi_{k,k}(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg]-\lambda\\ &\approx&\frac{ M(\alpha)}{1-\alpha}\bigg[1-\frac{\alpha h}{2(1-\alpha)}\bigg]-\lambda, \end{eqnarray*} $
由$\lambda<0$ $h<\frac{2(1-\alpha)}{\alpha}$ $b_{ii}>0, i=1,2,\cdots,N.$
根据$b_{12}$ $b_{21}$
(4.8) $\begin{eqnarray*}\label{4.8} b_{12}&=&\frac{ M(\alpha)}{1-\alpha}\int_{t_0}^{t_{1}}\omega_{2}'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\\ &=&\frac{ M(\alpha)}{1-\alpha}\int_{t_0}^{t_{1}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\omega_{2}(\tau)\\ &=&\frac{ M(\alpha)}{1-\alpha}\bigg[\omega_{2}(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})\bigg|_{t_0}^{t_{1}} -\int_{t_0}^{t_{1}}\frac{\alpha}{1-\alpha}\omega_{2}(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg]\\ &=&0,\\ \end{eqnarray*}$
(4.9) $\begin{eqnarray*} \label{4.9} b_{21}&=&\frac{ M(\alpha)}{1-\alpha}\int_{t_1}^{t_{2}}\varphi_{2,1}'(\tau)\exp(-\alpha\frac{t_{2}-\tau}{1-\alpha}){\rm d}\tau+\frac{ch M(\alpha)}{1-\alpha}\\ &&-\frac{ \alpha M(\alpha)}{(1-\alpha)^2}\int_{t_0}^{t_{1}}\frac{\alpha}{1-\alpha}\varphi_{2,1}(\tau)\exp(-\alpha\frac{t_{2}-\tau}{1-\alpha}){\rm d}\tau\\ &=&\frac{ \alpha hM(\alpha)}{(1-\alpha)^{2}}\exp(-\frac{\alpha h}{1-\alpha}), \end{eqnarray*}$
结合(4.6)-(4.9)式, $0<\alpha<1$ $h<\frac{2(1-\alpha)}{\alpha}$
(4.10) $\begin{equation}\label{4.10} b_{11}b_{22}-b_{21}b_{12} =\bigg[\frac{ M(\alpha)}{1-\alpha}(1-\frac{\alpha h}{2(1-\alpha)})-\lambda\bigg]^2 > 0. \end{equation}$
${\bf 定理 4.1}$ $h<\frac{2(1-\alpha)}{\alpha}$ $u_{0}$ $f(t)$ $U=(u_{1},u_{2},\cdots,u_{N})^{T}$ .
(4.11) $\begin{equation}\label{4.11} B_{2}U_{2}=F_{2}, \end{equation}$
其中 $B_{2}=\left( \begin{array}{cc} b_{11}~ & b_{12} \\ b_{21}~& b_{22} \\ \end{array} \right),$ $U_{2}=(u_{1},u_{2})^{\top},$ $F_{2}=(\tilde{f}_{1}, \tilde{f}_{2})^{\top}.$
根据引理4.1的(4.10)式, $| B_2| \neq 0$ $U_2$ . 进一步, 该文求解$N-2$
(4.12) $\begin{equation}\label{4.12} \begin{array}{lll} \begin{array}{lll}B_{N-2}U_{N-2}=F_{N-2},\end{array} \end{array} \end{equation} $
其中 $U_{N-2}=(u_3,u_4,\cdots, u_N)^{\top}, F_{N-2}=(\tilde{f}_{3},\tilde{f}_{4},\cdots,\tilde{f}_{N})^{\top}, B_{N-2}=(b_{ij}), j\leq i, i,j=3,\cdots,N$ $B_{N-2}$ $U_{N-2}$ . 证毕.
4.2 误差估计
${\bf 定理 4.2}$ $u(t)\in C^{4}[T]$
$| R_{k}| =O(h^4), h=\frac{T}{N}.$
${\bf证}$ $k=1$
(4.13) $\begin{eqnarray*}\label{4.13} | R_{1}| &=&\bigg| \frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau -(a_{1,0}u_{0}+a_{1,1}u_{1}+a_{1,2}u_{2})\bigg| \\ &=&\bigg| \frac{M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau \\ &&-\frac{M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}[\omega_{0}'(\tau)u_{0} +\omega_{1}'(\tau)u_{1}+\omega_{2}'(\tau)u_{2}]\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &=&\bigg| \frac{M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau-\frac{M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}[(\varphi_{1,0}(\tau)+\frac{3}{8}\varphi_{1,1}(\tau))'u_{0}\\ &&+(\varphi_{1,2}(\tau)+\frac{3}{4}\varphi_{1,1}(\tau))'u_{1}-\frac{1}{8}\varphi_{1,1}(\tau)'u_{2}]\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &=&\bigg| \frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau-\frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}(I_{1}u(\tau))'\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &\leq&\frac{ M(\alpha)}{1-\alpha}\bigg| \int_{0}^{t_{1}}[u(\tau)-I_{1}u(\tau)]'\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &=&\bigg| \frac{ M(\alpha)}{1-\alpha}\int_{0}^{t_{1}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}[u(\tau)-I_{1}u(\tau)]\bigg| \\ &\leq&\frac{ M(\alpha)}{1-\alpha}\bigg| \frac{u'''(\xi)}{3!}(\tau-t_{0})(\tau-t_{\frac{1}{2}})(\tau-t_{1})\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})\Big| _{t_{0}}^{{t_1}}\\ &&-\int_{0}^{t_{1}}\frac{u'''(\xi)}{3!}(\tau-t_{0})(\tau-t_{\frac{1}{2}})(\tau-t_{1}){\rm d} \exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})\bigg| \\ &\leq&\frac{\alpha M(\alpha)}{(1-\alpha)^2}\bigg| \frac{u'''(\xi)}{3!}h^{3}\int_{0}^{t_{1}}{\rm d}\tau \bigg| =O(h^4). \end{eqnarray*}$
其次, 考虑误差$R_{k}, 2\leq k\leq N$ $R_{k}$ $D_{h}^{I}(t_{k})$ $D_{h}^{II}(t_{k})$ $R_{k}^{1}$ $R_{k}^{2}$ . 应用$u(\tau)$ $\prod_{2,k}$
(4.14) $\begin{eqnarray*} \label{4.14} &&u(\tau)-\prod_{2,k}u(\tau)=\frac{u'''(\xi)}{3!}(\tau-t_{k-1})(\tau-t_{k-2})(\tau-t_{k}), \xi\in (t_{k-2},t_{k}), \end{eqnarray*} $
(4.15) $\begin{eqnarray*} \label{4.15} | R_{k}^{1}| &=&\bigg| \frac{ M(\alpha)}{1-\alpha}\int_{t_{k-1}}^{t_{k}}u'(\tau)\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau -(a_{k,k-2}u_{k-2}+a_{k,k-1}u_{k-1}+a_{k,k}u_{k})\bigg| \\ &=&\bigg| \frac{M(\alpha)}{1-\alpha}\int_{t_{k-1}}^{t_{k}}u'(\tau)\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau -\frac{M(\alpha)}{1-\alpha}\int_{t_{k-1}}^{t_{k}}[\prod_{2,k}u(\tau)]'\exp(-\alpha\frac{t_{k}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &\leq& \frac{M(\alpha)}{1-\alpha}\bigg| \int_{t_{k-1}}^{t_{k}}[u(\tau)-\prod_{2,k}u(\tau)]'\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}\tau\bigg| \\ &=&\frac{M(\alpha)}{1-\alpha}\bigg| \int_{t_{k-1}}^{t_{k}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}){\rm d}[u(\tau)-\prod_{2,k}u(\tau)]\bigg| \\ &=&\frac{M(\alpha)}{1-\alpha}\bigg| \exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})[u(\tau)-\prod_{2,k}u(\tau)]\Big| _{t_{k-1}}^{t_{k}}\\ &&-\frac{\alpha}{1-\alpha}\int_{t_{k-1}}^{t_{k}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})[u(\tau)-\prod_{2,k}u(\tau)]{\rm d}\tau \bigg| \\ &=&\frac{\alpha M(\alpha)}{1-\alpha}\bigg| \int_{t_{k-1}}^{t_{k}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha})[u(\tau)-\prod_{2,k}u(\tau)]{\rm d}\tau\bigg | \\ &=&\frac{\alpha M(\alpha)}{1-\alpha}\bigg| \int_{t_{k-1}}^{t_{k}}\exp(-\alpha\frac{t_{1}-\tau}{1-\alpha}) \frac{u'''(\xi)}{3!}(\tau-t_{k-1})(\tau-t_{k-2})(\tau-t_{k}){\rm d}\tau\bigg| \\ &\leq& \max\limits_{\xi\in(t_{k-2},t_{k})}\frac{| u'''(\xi)| }{3!}h^4\\ &=&O(h^4). \end{eqnarray*}$
$R_{k}^{2}$ $H(t_{k})$ $| R_{k}^{2}| =O(h^4)$ . 综上所述, 此定理成立.
4.3 稳定性分析
${\bf引理 4.2}$ $h<\frac{2(1-\alpha)}{\alpha}$
(1) $| D| \neq 0, D_{1}<D, D_{2}<D,$
(3) $\beta_{i}>0, \tilde{\beta}_{i}>0, i=3,4,\cdots,N.$
${\bf证}$ $\lambda<0, h<\frac{2(1-\alpha)}{\alpha}$
(2)根据$b_{3i}, i=0,1,2$
(3) 本文把$\beta_{i}, (i=3,4,\cdots,N)$
现在, 证明$\beta_{i1}>0, \beta_{i2}>0.$ $\hat{a}_{2,0}>0, \lambda<0$ $0<\alpha<1$
下一步, 对$j$ $b_{ij}<0, j=1,2,\cdots,i-1.$
如果$j=1$ $\hat{a}_{2,1}>0, \hat{a}_{3,1}>0 $
所以 $\beta_{i2}=-\sum\limits_{j=1}^{i-1}b_{ij}>0, \beta_{i}>0.$ $\tilde{\beta}_{i}=b_{ii}-\lambda=\frac{ M(\alpha)}{1-\alpha}(1-\frac{\alpha h}{2(1-\alpha)})-2\lambda>0. $
${\bf 定理 4.3}$ $u_{0}>0, \lambda<0$ $h<\frac{2(1-\alpha)}{\alpha}$ $u_{i}$
(4.16) $\begin{equation}\label{4.16} 0<u_{i}<u_{0}, i=1,2,\cdots,N. \end{equation}$
由引理4.2的(1)可知, $| D| \neq 0, D_{1}-D<0, D_{2}-D<0$
(4.17) $\begin{equation}\label{4.17} 0<u_{i}<u_{0}, i=1,2. \end{equation}$
(4.18) $\begin{equation}\label{4.18} u_{i}=\bigg[(-b_{i0}-\lambda \exp(\frac{-\alpha t_i}{1-\alpha}))u_{0}-\sum\limits_{j=1}^{i-1}b_{ij}u_{j}\bigg]/(b_{ii}-\lambda),\end{equation}$
根据引理4.1和引理4.2的(2)可知, $b_{33}>0, b_{3i}<0, i=0,1,2$
进一步, 可以直接验证 $0<-b_{30}-\lambda \exp(\frac{-\alpha t_3}{1-\alpha})-b_{31}-b_{32}<(b_{33}-\lambda),$
(4.19) $\begin{equation}\label{4.19} 0<u_{3}<u_{0}. \end{equation}$
接下来, 本文用数学归纳法来证明剩下的结果. 假设(4.12)式成立$i=k-1\leq N,$ $i=k.$
(4.20) $\begin{equation}\label{4.20} u_{k}=\bigg[(-b_{k0}-\lambda \exp(\frac{-\alpha t_{k}}{1-\alpha}))u_{0}-\sum\limits_{j=1}^{k-1}b_{kj}u_{j}\bigg]/(b_{k k}-\lambda),\end{equation}$
不难证明, (4.16)式右边的系数都是正的. 该文从归纳假设中推导出 $u_{k}<\frac{\beta_{k}}{\tilde{\beta}_{k}}u_{0},$
由于方程组(4.5)对于常数解是精确的, 因此得到 $b_{k0}+\sum\limits_{j=1}^{k-1}b_{kj}=0,$ $\beta_{k}-\tilde{\beta}_{k}<0,$ $0<u_{k}<u_0.$
5 数值算例
该文下面将给出一些例子来说明本方案的可行性, 该算例所有的计算均是通过软件Mathematica12 实现得到的. 些例子的目的是为了证明所提出的快速高阶方案在收敛速度和CPU 时间方面的准确性和效率, 最后通过算例验证了算法的稳定性和正则性.
${\bf 例1}$ 7 ]中带有下面几个右端项$f(t,u(t))$
$ \begin{array}{lll} (1) f(t,u(t))=G(t),\\ (2) f(t,u(t))=G(t)-t^3+u(t),\\ (3) f(t,u(t))=G(t)+t^6-u^2(t),\\ \end{array}\\ $
其中$u(t)=t^3, M(\alpha)=1$ $ T=1$
表1 -表3 展示了$\alpha= 0.3,~0.7$ 7 ]中的算例进行了比较. CPU时间的叠加如图1 -图3 所示, 可以看出随着节点数量的增加, 快速方案比直接方案快得多.
图1
图2
图3
${\bf 例 2}$
其中解析解是$u(t)=\sin t,$ $T = 100$ . 从表4 的结果可以看出, 经过长时间的计算, 数值解可以很好地近似解析解. 算例表明, 该方法具有良好的稳定性.
${\bf 例3}$ $f$ $T$ $h$
参考文献
View Option
[1]
Oldham K B Spanier J . The Fractional Calculus . New York : Academic Press , 1974
[本文引用: 1]
[2]
Samko S Kilbas A A Marichev O . Fractional Integrals and Derivatives: Theory and Applications . Oxfordshire : Taylor & Francis , 1993
[本文引用: 1]
[3]
Du M Wang Z Hu H . Measuring memory with the order of fractional derivative
Sci Rep , 2013 , 3 3431
[本文引用: 1]
[4]
Michele C Mauro F . A new definition of fractional derivative without singular kernel
Progr Fract Differ Appl , 2015 , 1 2 ): 73 -85
[本文引用: 1]
[5]
Atangana A Baleanu D . New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model
arXiv preprint arXiv:1602.03408 , 2016
[本文引用: 1]
[6]
Cao J Xu C . A high order schema for the numerical solution of the fractional ordinary differential equations
J Comput Phys , 2013 , 38 154 -168
[本文引用: 1]
[7]
Cao J Wang Z Xu C . A high-order scheme for fractional ordinary differential equations with the Caputo Fabrizio derivative
Communications on Applied Mathematics and Computation , 2019 , 1 1 -21
DOI:10.1007/s42967-019-0010-2
[本文引用: 4]
[8]
Yang J Huang J Liang D Tang Y . Numerical solution of fractional diffusion-wave equation based on fractional multistep method
Appl Math Model , 2014 , 38 14 ): 3652 -3661
DOI:10.1016/j.apm.2013.11.069
URL
[本文引用: 1]
[11]
Jiang S Zhang J Zhang Q Zhang Z . Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations
Commun Comput Phys , 2017 , 21 3 ): 650 -678
DOI:10.4208/cicp.OA-2016-0136
URL
[本文引用: 1]
The computational work and storage of numerically solving the time fractional PDEs are generally huge for the traditional direct methods since they require totalmemory andwork, whereNTandNSrepresent the total number of time steps and grid points in space, respectively. To overcome this difficulty, we present an efficient algorithm for the evaluation of the Caputo fractional derivativeof orderα∈(0,1). The algorithm is based on an efficient sum-of-exponentials (SOE) approximation for the kernelt–1–αon the interval [Δt,T] with a uniform absolute errorε. We give the theoretical analysis to show that the number of exponentialsNexpneeded is of orderforT≫1 orforTH1 for fixed accuracyε. The resulting algorithm requires onlystorage andwork when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.
[12]
Huang J Tang Y vazquez L . Convergence analysis of a block-by-block method for fractional differential equations
Numer Math Theor Methods Appl , 2012 , 5 2 ): 229 -241
DOI:10.4208/nmtma
URL
[本文引用: 1]
[14]
Baffet D Hesthaven J . A kernel compression scheme for fractional differential equations
SIAM J Numer Anal , 2017 , 55 2 ): 496 -520
DOI:10.1137/15M1043960
URL
[本文引用: 1]
[15]
Baffet D Hesthaven J . High-order accurate adaptive kernel compression time-stepping schemes for fractional differential equaitons
J Sci Comput , 2017 , 72 3 ): 1169 -1195
DOI:10.1007/s10915-017-0393-z
URL
[本文引用: 1]
[16]
Deng W H . Finite element method for the space and time fractional Fokker-Planck equation
SIAM J Numer Anal , 2008 , 47 1 ): 204 -226
DOI:10.1137/080714130
URL
[本文引用: 1]
[17]
Ke R H Ng M K Sun H W . A fast direct method for block triangular Toeplitz-like with tri-diagonal block systems from time-fractional partial differential equations
J Comput Phys , 2015 , 303 203 -211
DOI:10.1016/j.jcp.2015.09.042
URL
[本文引用: 1]
[18]
Liu F Shen S Anh V Turner I . Analysis of a discrete non-Markovian random walk approximation for the time fractional diffusion equation
ANZIAM J , 2005 , 46 C488 -C504
[本文引用: 1]
[19]
McLean W . Fast summation by interval clustering for an evolution equation with memory
J Sci Comput , 2012 , 34 6 ): A3039 -A3056
[本文引用: 1]
[20]
Hou D Xu C . A fractional spectral method with applications to some singular problems Adv Comput Math , 2017 , 343 5 ): 911 -944
[本文引用: 1]
[21]
Stynes M O'Riordan E Gracia J . Error analysis of a finite difference method of graded meses for a time-fractional Caputo-Fabrizio derivatives
Eur Phys J C , 2016 , 76 362
DOI:10.1140/epjc/s10052-016-4209-3
URL
[本文引用: 1]
1
1974
... 该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
1
1993
... 该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
Measuring memory with the order of fractional derivative
1
2013
... 该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
A new definition of fractional derivative without singular kernel
1
2015
... 该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model
1
2016
... 该文研究了一类带有非局部边界条件的微分方程数值求解,这类问题常应用于化学工程、热弹性学.在过去的几十年里, 分数微积分受到了物理学家和数学家的广泛关注, 因为它能准确地反映许多应用科学中的物理过程. 分数阶微分方程的数值分析已成为一个深入的研究课题. 分数阶微积分在近年来得到了广泛的研究[1 -2 ] . 它的研究结果可以说明若干物理问题[3 ] . Caputo和Fabrizio[4 ] 提出了一种新的分数阶导数. 另外, 在文献[5 ]中给出了具有非局部非奇异核的分数阶导数. 对于一般的右端函数$f$
A high order schema for the numerical solution of the fractional ordinary differential equations
1
2013
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
A high-order scheme for fractional ordinary differential equations with the Caputo Fabrizio derivative
4
2019
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
... 在文献[7 ]中, 该方程(1.1)的唯一解如下 ...
... ${\bf 例1}$ 7 ]中带有下面几个右端项$f(t,u(t))$
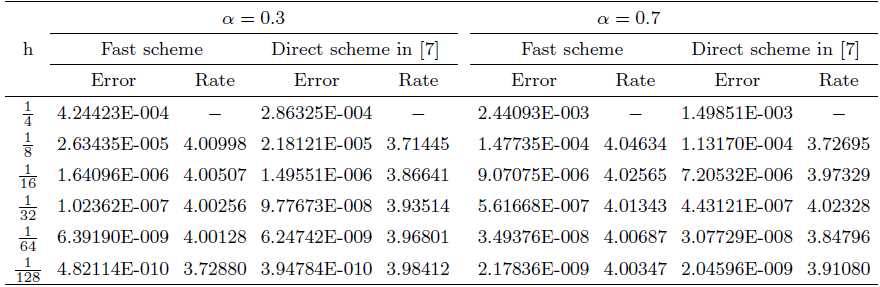
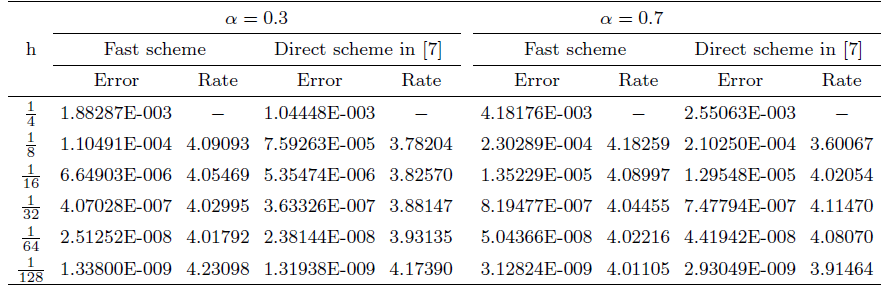
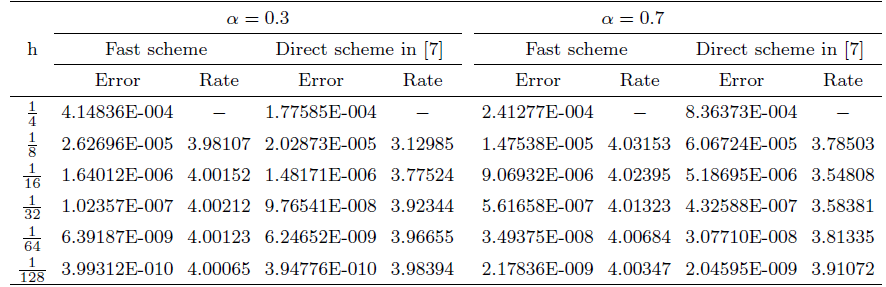
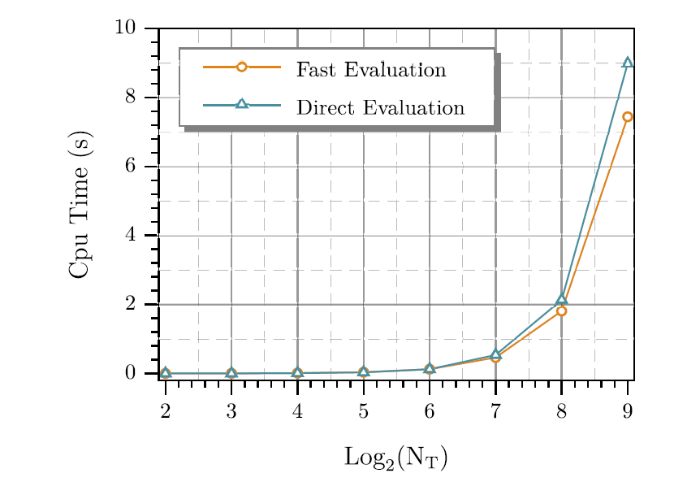
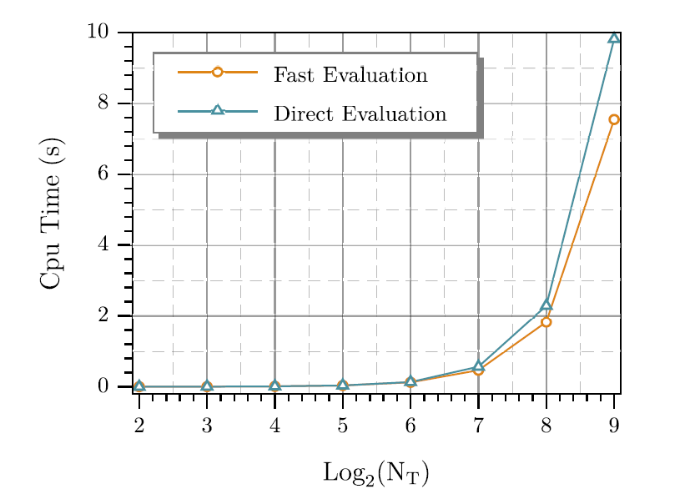
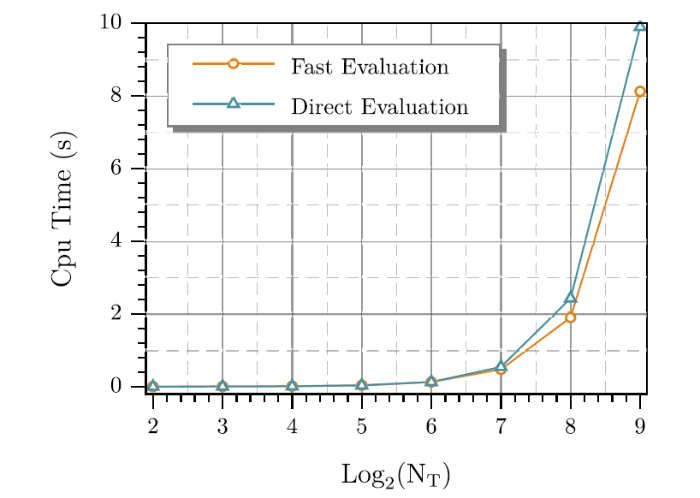
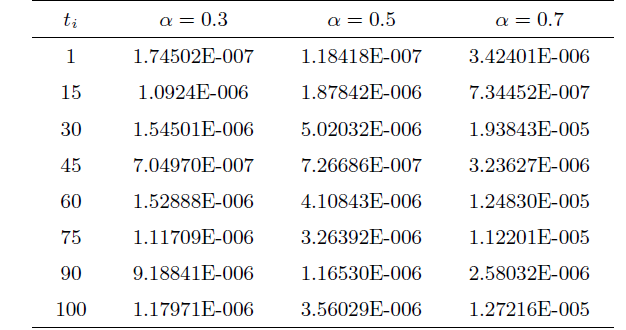
... 表1 -表3 展示了$\alpha= 0.3,~0.7$ 7 ]中的算例进行了比较. CPU时间的叠加如图1 -图3 所示, 可以看出随着节点数量的增加, 快速方案比直接方案快得多. ...
Numerical solution of fractional diffusion-wave equation based on fractional multistep method
1
2014
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
A fully discrete difference scheme for a diffusion-wave system
1
2006
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Finite difference/spectral approximations for the time-fractional diffusion equation
1
2007
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations
1
2017
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Convergence analysis of a block-by-block method for fractional differential equations
1
2012
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
A new difference scheme for the time fractional diffusion equation
1
2015
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
A kernel compression scheme for fractional differential equations
1
2017
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
High-order accurate adaptive kernel compression time-stepping schemes for fractional differential equaitons
1
2017
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Finite element method for the space and time fractional Fokker-Planck equation
1
2008
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
A fast direct method for block triangular Toeplitz-like with tri-diagonal block systems from time-fractional partial differential equations
1
2015
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Analysis of a discrete non-Markovian random walk approximation for the time fractional diffusion equation
1
2005
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Fast summation by interval clustering for an evolution equation with memory
1
2012
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
1
2017
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
Error analysis of a finite difference method of graded meses for a time-fractional Caputo-Fabrizio derivatives
1
2016
... Cao和Xu[6 -7 ] 考虑了分数阶常微分方程, 给出了一种改进的逐块逼近分数阶时间导数的方法. Yang[8 ] 等致力于分数阶多步方法在分数阶扩散波方程中的应用. Sun 和Wu[9 ] 以及Lin和Xu[10 ] 分别提出了时间分数阶扩散方程时间离散的$L1$ $2-\alpha$ . Jiang[11 ] 等给出了近似Caputo分数阶导数的快速逼近方法, 它是基于指数渐进法. Huang[12 ] 等证明了该方法的收敛性至少是3阶的. 在文献{[13 ⇓ ⇓ ⇓ ⇓ ⇓ -19 ]} 中学者们研究了时间分数阶扩散方程的快速求解, 在文献[20 -21 ] 中研究了解的起始时间奇点性的特别处理. ...
