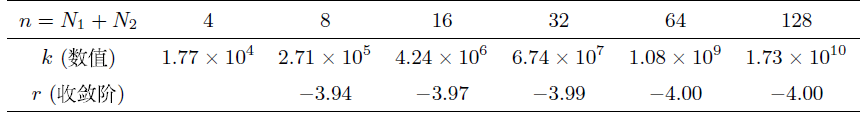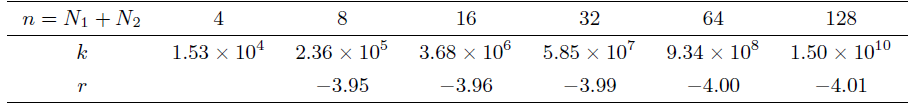1 引言
在椭圆型界面问题中, 通常由不同的材料构成模拟区域, 这些区域由曲线或曲面隔开. 在许多文献中已经讨论了处理跳跃条件的数值方法, 例如有限差分法[5,7-8], 有限元方法[9⇓⇓-12]. 有限元方法虽然经常被使用, 但通常的平均误差估计不能保证在界面附近或在界面处的解的精度. 对于有限差分方法, 混合导数的离散化和收敛分析是一个具有挑战性的问题. 值得一提的是, 董、冯等人在文献[13] 中提出了一种新的有限元-有限差分(FE-FD) 方法,该方法将系数矩阵为对称半正定的有限元离散(远离界面)和系数矩阵部分具有M 矩阵性质的有限差分(靠近界面或在界面上)相结合, 采用基于浸没界面法的插值法, 精确地计算了界面两侧解(或梯度)的法向导数. 此外, 潘、吴等人在文献[14]中提出了界面拟合网格生成(EIFMG)算法, 和保线性有限体积(FV)格式, EIFMG算法通过弯曲单元边缘以与材料界面对齐, 在不改变单元总数和相关拓扑的情况下生成与材料界面精确匹配的结构化曲面四边形网格. 其次, 通过使用所谓的线性保持准则, 导出的FV格式即使在极粗的网格上也能在具有线性解的弯曲四边形网格上精确求解, 这通常是有限元或有限差分方法不容易实现的. 在文献[15-16] 中, 作者通过改变界面所在单元的基函数设计了浸没有限元方法(IFEM). 同样的方法也应用于浸没有限体积法[17-18].
假定存在界面
其中
及界面
其中,
由于解的导数的不连续性, 传统的再生核空间
2 预备知识
定义2.2 [29] W12[a,b]={f(x)|f(x)在[a,b]上是绝对连续的实值函数,f′(x)∈L2[a,b]} 是具有再生核K(x,y)的再生核空间.其内积和范数表示为
下面我们定义一个三次样条空间.
接下来, 我们给出空间
设
假设存在
因为
两边同时求二阶导可得
设
所以
进而有
因为
由此我们可知
为了求解方程组(1.1)-(1.3), 我们在
其中
分别是
接下来, 我们给出空间
设
其中
{\bf 引理2.2} {V}_{N_1,N_2}[0,1]=span\{\Phi_1,\Phi_2,\cdots,\Phi_{N_1},\Psi_1,\Psi_2,\cdots,\Psi_{N_2}, \Upsilon_1,\Upsilon_2,\Upsilon_3,\Upsilon_4.
假设存在
当
两边同时求二阶导可得
由引理
同理可得, 当
由此可得
下面给出样条插值函数的收敛性, 其证明我们不再仔细讨论, 有兴趣的读者可以参考文献[31].
其中,
3 利用最小二乘法求解方程组(1.1)-(1.3)
定义两个线性算子
再定义一个线性算子
此时, 方程(1.1)-(1.3)等价于如下的算子方程
我们在
接下来我们确定未知系数
对任意的
其中
对任意的
其中
方程(3.5)与(3.4)等价.
所以我们有
因此,
算子方程有唯一解
4 误差分析
用
则
由上式和方程(2.3)可知
证毕.
类似地, 我们可以在
令
进而通过计算,我们有
因为
此外,我们有
令
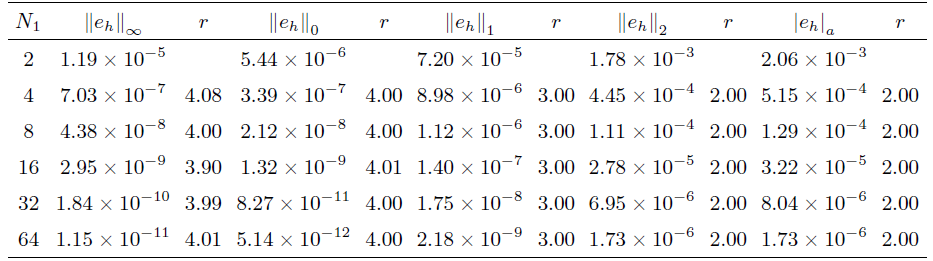
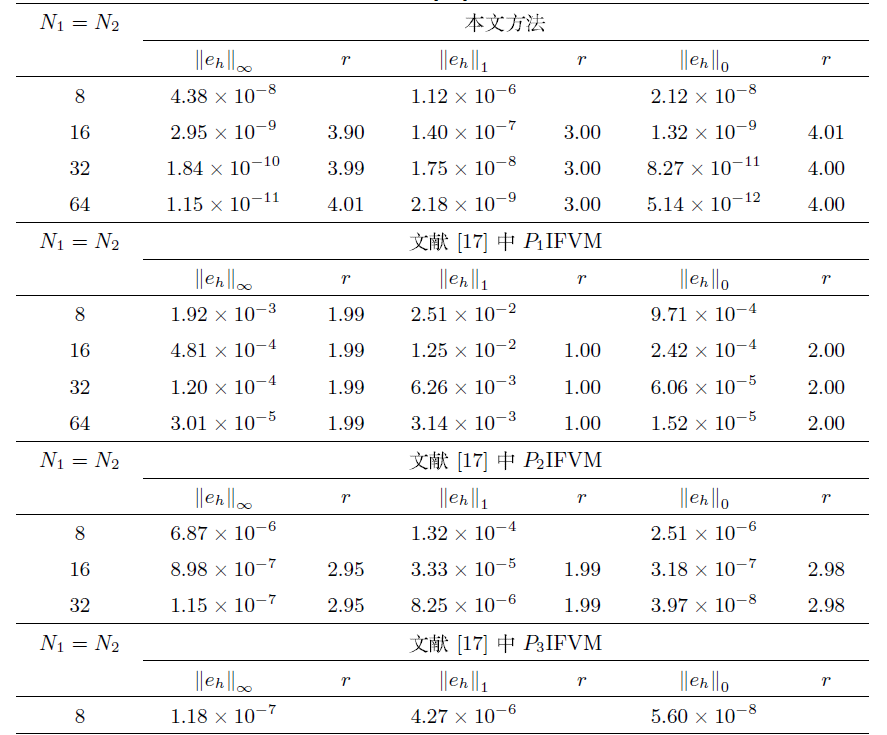
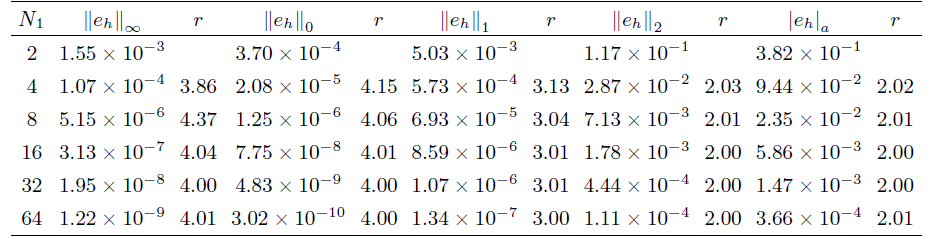
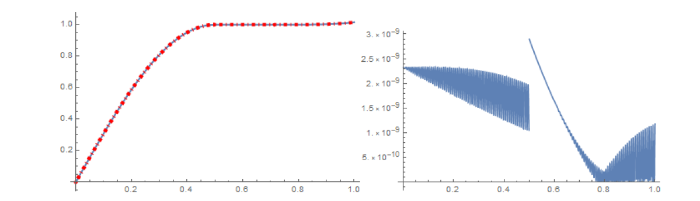
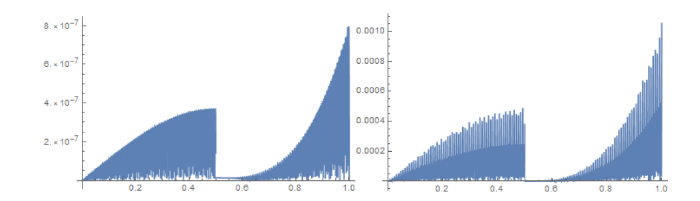
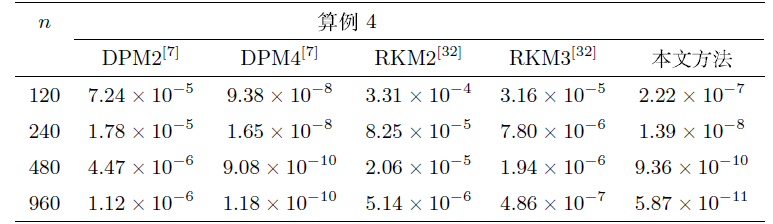
5 数值算例
满足的边界及界面条件为
其中
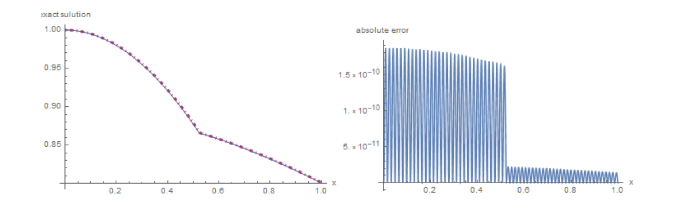
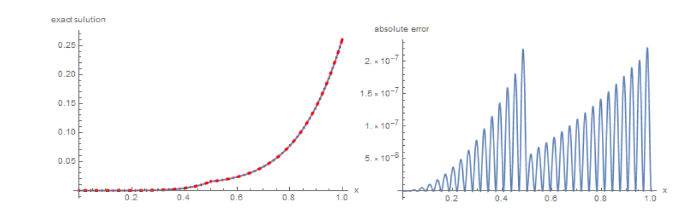
图 1
满足的边界及界面条件为
其中
图 2
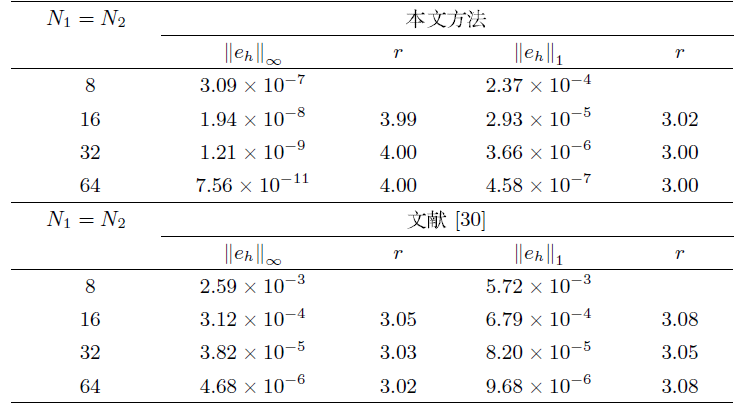
满足的边界及界面条件为
其中,
其中,
图 3
图 4
6 结论
在本文中, 我们通过积分
参考文献
On the numerical evaluation of electrostatic fields in composite materials
DOI:10.1017/S0962492900002464
URL
[本文引用: 1]

A classical problem in electrostatics is the determination of the effective electrical conductivity in a composite material consisting of a collection of piecewise homogeneous inclusions embedded in a uniform background. We discuss recently developed fast algorithms for the evaluation of the potential and electrostatic fields induced in multiphase composites by an applied potential, from which the desired effective properties may be easily obtained. The schemes are based on combining a suitable boundary integral equation with the Fast Multipole Method and the GMRES iterative method; the CPU time required grows linearly with the number of points in the discretization of the interface between the inclusions and the background material.
Computational algorithm for solving Fredholm time-fractional partial integrodifferential equations of Dirichlet functions type with error estimates
DOI:10.1016/j.amc.2018.09.020 URL [本文引用: 1]
Numerical investigations for systems of second-order periodic boundary value problems using reproducing kernel method
DOI:10.1016/j.amc.2016.06.002 URL [本文引用: 1]
High-order numerical schemes based on difference potentials for 2D elliptic problems with material interfaces
DOI:10.1016/j.apnum.2016.08.017 URL [本文引用: 2]
Special finite element methods for a class of second order elliptic problems with rough coefficients
DOI:10.1137/0731051 URL [本文引用: 1]
High-order difference potentials methods for 1D elliptic type models
DOI:10.1016/j.apnum.2014.02.005 URL [本文引用: 5]
A second order virtual node method for elliptic problems with interfaces and irregular domains in three dimensions
DOI:10.1016/j.jcp.2011.11.023 URL [本文引用: 1]
Preconditioning for finite element methods with strain smoothing
DOI:10.1016/j.camwa.2022.11.018 URL [本文引用: 1]
Generalized Multiscale Finite Element Method for scattering problem in heterogeneous media
DOI:10.1016/j.cam.2022.114977 URL [本文引用: 1]
On the accuracy of finite element approximations to a class of interface problems
DOI:10.1090/mcom/2016-85-301 URL [本文引用: 1]
Analysis of an efficient finite element method for embedded interface problems
An FE-FD method for anisotropic elliptic interface problems
DOI:10.1137/19M1291030 URL [本文引用: 1]
An exact-interface-fitted mesh generator and linearity-preserving finite volume scheme for anisotropic elliptic interface problems
DOI:10.1016/j.jcp.2022.111293 URL [本文引用: 1]
Superconvergence of immersed finite element methods for interface problems
DOI:10.1007/s10444-016-9507-7 URL [本文引用: 1]
Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions
Superconvergence of immersed finite volume methods for one-dimensional interface problems
DOI:10.1007/s10915-017-0532-6 [本文引用: 4]
Analysis of a special immersed finite volume method for elliptic interface problems
Reproducing kernel particle method
DOI:10.1002/(ISSN)1097-0363 URL [本文引用: 1]
Weighted reproducing kernel collocation method and error analysis for inverse Cauchy problems
DOI:10.1142/S1758825116500307
URL
[本文引用: 1]

In this work, the weighted reproducing kernel collocation method (weighted RKCM) is introduced to solve the inverse Cauchy problems governed by both homogeneous and inhomogeneous second-order linear partial differential equations. As the inverse Cauchy problem is known for the incomplete boundary conditions, how to numerically obtain an accurate solution to the problem is a challenging task. We first show that the weighted RKCM for solving the inverse Cauchy problems considered is formulated in the least-squares sense. Then, we provide the corresponding error analysis to show how the errors in the domain and on the boundary can be balanced with proper weights. The numerical examples demonstrate that the weighted discrete systems improve the accuracy of solutions and exhibit optimal convergence rates in comparison with those obtained by the traditional direct collocation method. It is shown that neither implementation of regularization nor implementation of iteration is needed to reach the desired accuracy. Further, the locality of reproducing kernel approximation gets rid of the ill-conditioned system.
Weighted reproducing kernel collocation method based on error analysis for solving inverse elasticity problems
DOI:10.1007/s00707-019-02473-0 [本文引用: 1]
Reproducing kernel enhanced local radial basis collocation method
An efficient reproducing kernel method for solving the allen-cahn equation
DOI:10.1016/j.aml.2018.09.013 URL [本文引用: 1]
A reproducing kernel method for solving heat conduction equations with delay
DOI:10.1016/j.aml.2019.106036 URL [本文引用: 1]
A new piecewise reproducing kernel function algorithm for solving nonlinear hamiltonian systems
DOI:10.1016/j.aml.2022.108451 URL [本文引用: 1]
A high order convergence collocation method based on the reproducing kernel for general interface problems
DOI:10.1016/j.aml.2020.106718 URL [本文引用: 1]
A reproducing kernel method for nonlinear C-q-fractional IVPs
DOI:10.1016/j.aml.2021.107751 URL [本文引用: 1]
椭圆型界面问题的破裂再生核方法
DOI:10.12286/jssx.j2021-0791
[本文引用: 3]

本文基于一维椭圆型界面问题提出了一种有效的数值方法.首先,根据模型构建一个崭新的破裂再生核空间.其次,应用破裂再生核方法给出了此类界面问题的近似解,并讨论该方法的收敛性.最后,通过几个有效的数值算例来说明该方法的精确性和稳定性.
The method of fracture regeneration core for elliptical interface problem
DOI:10.12286/jssx.j2021-0791
[本文引用: 3]

本文基于一维椭圆型界面问题提出了一种有效的数值方法.首先,根据模型构建一个崭新的破裂再生核空间.其次,应用破裂再生核方法给出了此类界面问题的近似解,并讨论该方法的收敛性.最后,通过几个有效的数值算例来说明该方法的精确性和稳定性.
Optimal error bounds for cubic spline interpolation
DOI:10.1016/0021-9045(76)90040-X URL [本文引用: 1]
A simplified reproducing kernel method for 1-D elliptic type interface problems
DOI:10.1016/j.cam.2018.10.027 URL [本文引用: 3]