1 引言
非线性Maxwell方程在科学工程相关领域普遍存在. 其中, 具有依赖于场源的非线性电导率的Maxwell方程应用在多个物理模型中, 例如第二型超导体的本构定律、NbSe3的电荷密度波态等[5-6]. 关于非线性Maxwell方程弱解的存在唯一性以及当
非一致介质Maxwell方程中的介电常数和磁导率在跨过不同的介质时会产生跳跃, 从而使解产生间断. 电磁场间断解问题的数值计算, 有一定的难度和挑战性, 促使很多学者从事这方面的研究并提出了一些有效的数值方法, 如高阶嵌入FDTD和导数匹配法、匹配和沉浸交界面(IIM)法、间断Galerkin(DG)方法等[15⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-26]. Zhao等[18]讨论了非一致介质中具有间断解的Maxwell方程的数值解法, 提出了高阶的隐式分层的导数匹配方法(HDM-FDTD). 此方法在介质交界面处增加虚拟点和附加的连接条件, 利用高阶跳跃条件来得到高精度, 如采用多于
谱方法数值求解非线性系统的理论不断发展完善起来[27⇓⇓⇓-31]. Ma[32-33]讨论了非线性守恒方程的Chebyshev-Legendre耦合谱方法, 提出谱粘性(CLSV)和超谱粘性的方法. Ma和Sun[34]提出了一种广义的Legendre-Petrov-Galerkin谱方法求解KdV方程, 对非线性项采用了Chebyshev谱配置方法, 并证明了半离散和全离散格式
基于上述研究工作, 本文考虑了非线性非一致介质二维Maxwell方程的数值求解方法, 提出了leap-frog Crank-Nicolson(LFCN)多区域Legendre-tau配置(MLTC)谱方法. 本数值方法空间上达到谱精度, 时间上是二阶精度. 此数值方法采用tau方法思想, 针对电场和磁场的不同特性, 定义不同次多项式空间来逼近电磁场. 利用显隐数值格式, 对线性和非线性项采用不同的处理方式, 对线性项采用Legendre谱方法隐式处理, 而对于非线性项部分采用谱配置法来显式处理, 可以是Legendre-Gauss-Lobatto(LGL)配置点, 也可以是Chebyshev-Gauss-Lobatto(CGL)配置点等. 这样, 数值方法既具有较好的稳定性又方便算法实施. 对非一致介质, 本文主要考虑规则介质交界面的情形, 并假设介电常数和磁导率是计算区域上的分片常数函数. 此方法自然地在介质交界处进行区域剖分, 基于合理的弱形式, 采用类似自然边界条件的方式处理交界面条件, 不需要使用附加的连接条件, 构建一致的数值格式, 并获得谱精度. 我们在时间方向采用LFCN格式离散, 该方法结合非线性部分的leap frog显隐格式和线性高阶导数部分的Crank-Nicolson隐式格式, 早期由文献[36]提出应用于Korteweg-de Vries 方程的Fourier谱方法, 并进行了线性化稳定性分析. 本文详细证明了非线性问题LFCN数值格式的稳定性和收敛性, 并得到
2 预备记号和问题弱形式
设
其中
和初始条件
非一致介质电磁场中的介电常数
其中
下面以上述交界面情况为例, 说明一下方程解是满足交界面条件(2.6)式的. 由(2.1)-(2.3)式知, 解
记
二维非线性间断解Maxwell方程(2.1)-(2.4)的弱形式可写为: 求
这里假设介质被分成不同的矩形块,
3 多区域Legendre-tau配置谱方法半离散格式
本节给出问题(2.1)-(2.5)的多区域Legendre-tau配置谱方法半离散格式, 并证明格式的稳定性和收敛性.
3.1 半离散格式
记
并设
设
以及逼近空间
记参考区间
定义分片连续函数空间
建立函数在子区域
设插值算子
i. LGL插值算子
ii. CGL插值算子
定义如下
下面给出问题(2.1)-(2.5)的多区域Legendre-tau配置谱方法半离散格式: 求
其中
3.2 稳定性分析
在数值分析过程中, 考虑
对于多区域的情况, 如果
注意到Legendre多项式有性质
因此得到结论(3.5)式.
对于多区域情况, 注意到
因此得到结论(3.6)式.
定义分裂Sobolev空间
及其上范数
进一步可得到下面的逼近引理.
设
其中,
在扰动方程(3.9)-(3.11)中, 令
从而有
这里
下面来估计非线性项. 定义如下离散范数
其中
因此有
类似地, 有
现估计非线性项
引入记号
令
为了方便表达, 在下面的证明过程中, 我们将会省略记号
由微分中值定理得
其中
其中
因此, 对于
对
令
综上可得, 在条件(3.15)式满足时
记
否则存在
由(3.21)式, 并根据Gronwall不等式, 得
根据引理3.1, 有
这与(3.24)式矛盾, 从而(3.23)式成立. 因此,
3.3 收敛性分析
下面先给出误差估计时要用到的投影算子. 定义
注意到
类似地, 定义
由算子
类似地
现给出下面的逼近引理.
取比较函数
其中,
令
其中,
类似前面半离散格式稳定性的讨论过程, 有如下收敛性定理.
类似定理3.1的证明过程, 如果
接下来估计截断误差
对于
记
进而根据引理3.3得
因此,
再由引理3.2和引理3.3, 以及三角不等式, 就证得收敛性定理.
4 leap-frog Crank-Nicolson多区域Legendre-tau配置谱方法全离散格式
本节给出问题(2.1)-(2.5)的LFCN多区域Legendre-tau配置谱方法全离散格式, 并证明全离散格式的稳定性和收敛性.
4.1 全离散格式
设
下面给出问题(2.1)-(2.5)的LFCN多区域Legendre-tau配置(LFCN-MLTC) 谱方法的三层全离散格式: 求
初始值取为
4.2 稳定性分析
假设解和右端分别有扰动
其中
在(4.5)-(4.7)式中, 分别取
整理可得
这里
下面估计(4.8)式中的非线性项. 类似(3.13)式可得
类似半离散非线性项的估计(3.18)式, 当
同理可得
对于右端误差
结合(4.10), (4.11)和(4.12)式, 由(4.8)式可得, 对于
上式关于
令
并且定义
综上可得, 对于
从而有如下稳定性定理.
首先对于
所以对
因此,
4.3 收敛性分析
本节讨论LFCN-MLTC谱方法全离散格式(4.1)-(4.3)式的收敛性, 并证明对于Legendre插值情况下的
引入合适的比较函数
记
给出下列截断误差方程
其中
由投影算子
令
其中, 记
由稳定性结论, 可以得到下面收敛性定理.
对于
对于
类似地, 可得
接着估计右端误差. 对
利用分部积分, 有
进一步, 可得
从而结合引理3.3有
类似(3.39)式及上式的推导, 可估计得到
因此
同理可得
因此, 对任意的
故当
再结合三角不等式, 并利用引理3.2和引理3.3, 即证得收敛性结论.
5 数值算例
在本节中, 给出充分的数值算例来验证理论分析结果, 证实LFCN-MLTC方法求解非线性问题的有效性和高精度. 在算例中, 对非线性项采用Chebyshev插值, 选取CGL插值节点, 结合快速Legendre变换(FLT), 提高计算效率.
为了验证算法精度和有效性, 定义移位CGL点
取解
其中
本算例中, 考虑非一致介质中具有非线性电导率的Maxwell方程间断解问题. 此时问题的解在交界面处会出现间断或弱间断. 这里假设介电常数
设跳跃的介电常数
取
记
右端项可由方程得到.
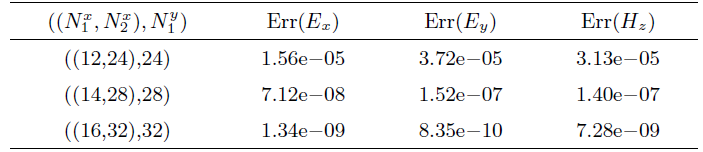
现来验证LFCN-MLTC法的误差精度. 计算时, 取
并记
右端项可由方程得到.
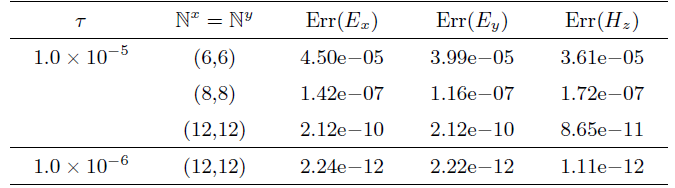
同样地,
并记
表5
取
 |
右端项为
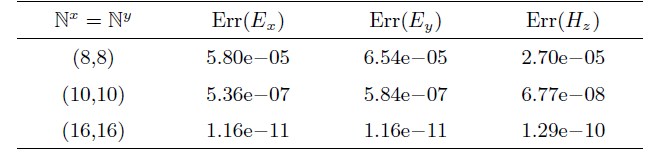
现验证本文方法的误差精度. 计算时,
取
表7
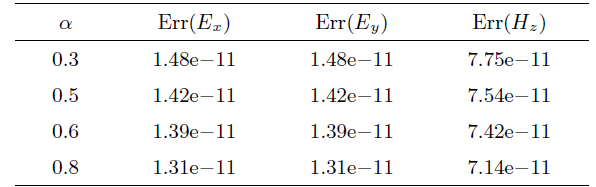
取
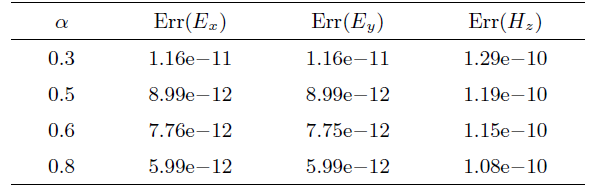 |
6 结论
本文讨论了具有非线性电导率的非一致介质的二维Maxwell方程的数值求解方法, 提出了LFCN多区域Legendre-tau配置谱方法. 此数值方法采用显隐数值格式, 对线性和非线性部分分别采用不同的处理方法. 线性项采用Legendre谱方法隐式处理, 非线性项采用谱配置法来显式处理. 此方法采用不同次的多项式空间逼近电磁场, 基于合理的弱形式, 逼近格式不需要使用额外附加的交界面连接条件, 构建一致的数值格式, 简化计算, 同时很好地保持了谱精度. 时间方向上采用分裂的LFCN三层格式. 非线性项放在中间已知层来处理. 给出半离散和全离散格式, 并证明了数值格式的稳定性和收敛性, 对于Legendre插值的情况得到了
参考文献
Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media
Nonlinear diffusion in type-II superconductors
DOI:10.1016/j.cam.2006.03.055 URL [本文引用: 1]
Nonlinear conductivity and noise due to charge-density-wave depinning in nbse3
DOI:10.1103/PhysRevLett.46.511 URL [本文引用: 1]
On a singular limit problem for nonlinear Maxwell's equations
DOI:10.1006/jdeq.1998.3608 URL [本文引用: 1]
Asymptotic behavior of the electromagnetic field for a micromagnetism equation without exchange energy
DOI:10.1137/S0036141004443324 URL [本文引用: 1]
Existence and regularity of a weak solution to Maxwell's equations with a thermal effect
DOI:10.1002/(ISSN)1099-1476 URL [本文引用: 2]
Orthogonal decomposition and asymptotic behavior for nonlinear Maxwell's equations
DOI:10.1016/j.jmaa.2014.12.071 URL [本文引用: 1]
Convergence of the mixed finite element method for Maxwell's equations with nonlinear conductivity
DOI:10.1002/mma.v35.13 URL [本文引用: 1]
A third order linearized BDF scheme for Maxwell's equations with nonlinear conductivity using finite element method
High spatial order energy stable FDTD methods for Maxwell's equations in nonlinear optical media in one dimension
DOI:10.1007/s10915-018-0716-8 [本文引用: 1]
A time-domain finite element scheme and its analysis for nonlinear Maxwell's equations in Kerr media
DOI:10.1016/j.jcp.2021.110259 URL [本文引用: 1]
High-order accurate methods in time-domain computational electromagnetics: A review
A staggered fourth-order accurate explicit finite differences scheme for the time-domain Maxwell's equations
DOI:10.1006/jcph.2001.6691 URL [本文引用: 1]
An explicit fourth-order staggered finite-difference time-domain method for Maxwell's equations
DOI:10.1016/S0377-0427(02)00394-1 URL [本文引用: 1]
High-order FDTD methods via derivative matching for Maxwell's equations with material interfaces
DOI:10.1016/j.jcp.2004.03.008 URL [本文引用: 2]
Finite element methods with matching and nonmatching meshes for Maxwell equations with discontinuous coefficients
DOI:10.1137/S0036142998349977 URL [本文引用: 1]
An upwinding embedded boundary method for Maxwell's equations in media with material interfaces: 2D case
DOI:10.1016/S0021-9991(03)00269-9 URL [本文引用: 2]
On the immersed interface method for solving time-domain Maxwell's equations in materials with curved dielectric interfaces
DOI:10.1016/j.cpc.2008.07.001 URL [本文引用: 1]
Time-domain matched interface and boundary (MIB) modeling of Debye dispersive media with curved interfaces
DOI:10.1016/j.jcp.2014.08.038 URL [本文引用: 1]
Time-domain numerical solutions of Maxwell interface problems with discontinuous electromagnetic waves
DOI:10.4208/aamm.2014.m811
URL
[本文引用: 1]

This paper is devoted to time domain numerical solutions of two-dimensional (2D) material interface problems governed by the transverse magnetic (TM) and transverse electric (TE) Maxwell's equations with discontinuous electromagnetic solutions. Due to the discontinuity in wave solutions across the interface, the usual numerical methods will converge slowly or even fail to converge. This calls for the development of advanced interface treatments for popular Maxwell solvers. We will investigate such interface treatments by considering two typical Maxwell solvers – one based on collocation formulation and another based on Galerkin formulation. To restore the accuracy reduction of the collocation finite-difference time-domain (FDTD) algorithm near an interface, the physical jump conditions relating discontinuous wave solutions on both sides of the interface must be rigorously enforced. For this purpose, a novel matched interface and boundary (MIB) scheme is proposed in this work, in which new jump conditions are derived so that the discontinuous and staggered features of electric and magnetic field components can be accommodated. The resulting MIB time-domain (MIBTD) scheme satisfies the jump conditions locally and suppresses the staircase approximation errors completely over the Yee lattices. In the discontinuous Galerkin time-domain (DGTD) algorithm – a popular GalerkinMaxwell solver, a proper numerical flux can be designed to accurately capture the jumps in the electromagnetic waves across the interface and automatically preserves the discontinuity in the explicit time integration. The DGTD solution to Maxwell interface problems is explored in this work, by considering a nodal based high order discontinuous Galerkin method. In benchmark TM and TE tests with analytical solutions, both MIBTD and DGTD schemes achieve the second order of accuracy in solving circular interfaces. In comparison, the numerical convergence of the MIBTD method is slightly more uniform, while the DGTD method is more flexible and robust.
Optimal non-dissipative discontinuous Galerkin methods for Maxwell's equations in Drude metamaterials
DOI:10.1016/j.camwa.2017.02.018 URL [本文引用: 1]
A continuity-preserving and divergence-cleaning algorithm based on purely and damped hyperbolic Maxwell equations in inhomogeneous media
DOI:10.1016/j.jcp.2017.01.012 URL [本文引用: 1]
An HDG method for Maxwell's equations in heterogeneous media
DOI:10.1016/j.cma.2020.113178 URL [本文引用: 1]
Laguerre-Galerkin method for nonlinear partial differential equations on a semi-infinite interval
DOI:10.1007/PL00005413 URL [本文引用: 1]
Some Developments in Spectral Methods for Nonlinear Partial Differential Equations in Unbounded Domains//Gu C H, Hu H S, Li T. Differential Geometry and Related Topics
Chebyshev-Legendre spectral viscosity method for nonlinear conservation laws
DOI:10.1137/S0036142995293900 URL [本文引用: 1]
Chebyshev-Legendre super spectral viscosity method for nonlinear conservation laws
DOI:10.1137/S0036142995293912 URL [本文引用: 1]
Optimal error estimates of the Legendre-Petrov-Galerkin method for the Korteweg-de Vries equation
DOI:10.1137/S0036142900378327 URL [本文引用: 1]
Multidomain Legendre-Galerkin Chebyshev-collocation method for one-dimensional evolution equations with discontinuity
DOI:10.1016/j.apnum.2016.09.010 URL [本文引用: 1]
Fourier methods with extended stability intervals for the Korteweg-de Vries equation
DOI:10.1137/0722026 URL [本文引用: 1]
Chebyshev-Legendre spectral method for solving the two-dimensional vorticity equations with homogeneous Dirichlet conditions
DOI:10.1002/num.v25:3 URL [本文引用: 1]
Energy-conserved splitting multidomain Legendre-Tau spectral method for two dimensional Maxwell's equations
DOI:10.1007/s10915-021-01744-0 [本文引用: 1]