The propagation of nonlinear wave envelopes
1
1967
... 著名的非线性 Schrödinger 方程[1-2] ...
Propagation of wave packets and space-time self-focussing in a nonlinear medium
1
1967
... 著名的非线性 Schrödinger 方程[1-2] ...
1
1999
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
1
2015
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media
1
1972
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
1
1991
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
1
1991
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Darboux transformations for a Lax integrable system in 2n-dimensions
1
1997
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Rogue waves and rational solutions of the nonlinear Schr?dinger equation
1
2009
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Nonlinear Schr?dinger equation: generalized Darboux transformation and rogue wave solutions
1
2012
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Waves that appear from nowhere and disappear without a trace
1
2009
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
1
2008
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Optical rogue waves
1
2007
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Water waves, nonlinear Schr?dinger equations and their solutions
1
1983
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Discrete rogue waves of the Ablowitz-Ladik and Hirota equations
1
2010
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
High-order solutions and generalized Darboux transformations of derivative nonlinear Schr?dinger equations
2
2013
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
... 然后利用文献[16,21] 中的广义 Darboux 变换可得到方程 (1.2) 高阶畸形波解. ...
Dynamics of rogue waves in the Davey-Stewartson II equation
1
2013
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Persistence of rogue waves in extended nonlinear Schr?dinger equations: integrable Sasa-Satsuma case
1
2012
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Intricate dynamics of rogue waves governed by the Sasa-Satsuma equation
1
2020
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Solutions of the vector nonlinear Schr?dinger equations: evidence for deterministic rogue waves
1
1981
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Dynamics of rogue waves on a multisoliton background in a vector nonlinear Schr?dinger equation
2
2015
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
... 然后利用文献[16,21] 中的广义 Darboux 变换可得到方程 (1.2) 高阶畸形波解. ...
Financial rogue waves
1
2010
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Modulation instability and periodic solutions of the nonlinear Schr?dinger equation
1
1986
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
First-order exact solutions of the nonlinear Schr?dinger equation in the normal-dispersion regime
1
1993
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
General high-order rogue waves and their dynamics in the nonlinear Schr?dinger equation
1
2012
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Lump solutionsto nonlinear partial differential equations via Hirota bilinear forms
1
2018
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Exotic vector freak waves in the nonlocal nonlinear Schr?dinger equation
1
2022
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Initial-boundary value problems for the general coupled nonlinear Schr?dinger equation on the interval via the Fokas method
1
2017
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
PINN deep learning method for the Chen-Lee-Liu equation: Rogue wave on the periodic background
1
2022
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Several reverse-time integrable nonlocal nonlinear equations: Rogue-wave solutions
1
2018
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
The rogue wave and breather solution of the Gerdjikov-Ivanov equation
1
2012
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Vector nonlinear waves in a two-component Bose-Einstein Condensate system
1
2020
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
The three-component coupled nonlinear Schr?dinger equation: Rogue waves on a multi-soliton background and dynamics
1
2018
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
Characteristics of the breather and rogue waves in a (2+1)-dimensional nonlinear Schr?dinger equation
1
2018
... 是一个重要的非线性数学物理模型, 它可以反映许多重要物理现象, 并且有广泛的物理应用和实践前景. 另外, 由于其奇特的数学结构和丰富的物理意义, 非线性 Schrödinger 方程在数学和物理领域都发挥了重要的作用, 并取得了巨大的科研成果, 其中 ± 分别表示聚焦和散焦的情况. 实际上, 它也是非线性数学物理领域中一个基本的非线性系统[3-4]. 它是完全可积的, 许多学者通过反散射方法[5-6] 和 Darboux 变换法[7-8] 已经得到了该系统各种不同形式的非线性波解.在过去的几十年里, 它再次受到人们的广泛关注, 其主要原因是它可以用来刻画奇特的畸形波现象[9-10]. 畸形波, 也被称为怪波、杀人波等是一种自发性的巨浪且具有来无影去无踪的特征[11]. 近些年, 由于这类波突然性且破坏性的影响, 以至于吸引了人们广泛的关注[12-13]. 在 1983 年, Peregrine[14] 成功在方程(1.1)中推导出畸形波解的第一个解析表达式. 之后, 科研工作者们也在其他可积系统中刻画出了畸形波现象, 如Hirota 方程[15], 导数非线性 Schrödinger 方程[16], Davey-Stewartson 方程[17], Sasa-Satsuma 方程[18-19] 等[20⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-34]. ...
On Nth-order rogue wave solution to the generalized nonlinear Schr?dinger equation
2
2013
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
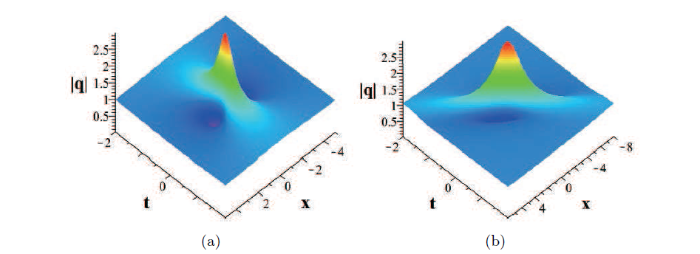
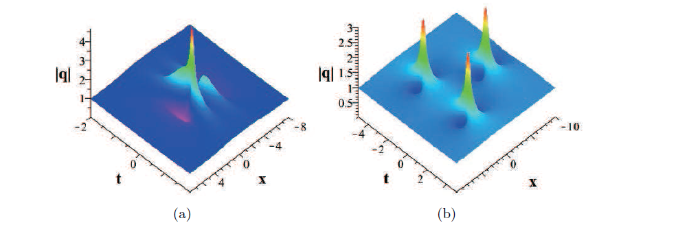
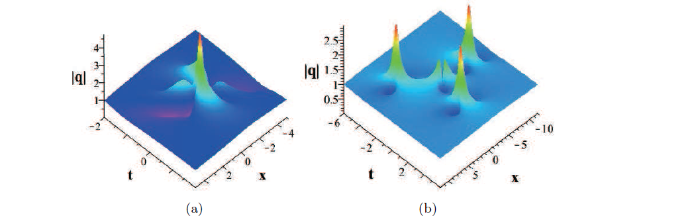
... 它包含非线性光学中的五次非线性项和 Raman 效应, 其中 q=q(x,t) 是一个复光滑波包函数, 下标表示对变量的偏导数, β 是一个实常数. 据我们所知, 目前已经存在许多有关方程 (1.2) 畸形波解的研究. 例如, 在文献[35] 中利用广义 Darboux 变换结合规范变换已经研究了方程 (1.2) 的 N-阶畸形波解. 在文献 [42]中, 利用广义 Darboux 变换结合 Taylor 展开式构造了方程 (1.2) 的高阶畸形波解并考虑了五次非线性项对解的动力学行为的影响. 在文献[43]中, 首先利用广义 Darboux 变换的相关理论知识构造了方程 (1.2) 的畸形波解, 然后通过数值计算和图像分析, 证明了五次非线性项和 Raman 效应非线性项能够影响高阶畸形波中驼峰的空间分布, 但驼峰的振幅和出现时间不变. 在他们的论文中, 为了利用广义 Darboux 变换得到方程 (1.2) 的畸形波解, 一个关键的步骤就是需要计算一系列相应特征函数的复导数. 但是在本文的第三节我们引入了方程 (1.2) Lax 对的解族, 该解族可以用变量分离形式的指数矩阵表示. 因此, 相比于其它论文利用广义 Darboux 变换对畸形波解的研究, 本文在推导畸形波解的显式表达式的过程中没有任何的导数计算, 这为构造方程的畸形波解提供了便利. ...
Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schr?dinger-type equations
1
1984
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
An exact solution for a derivative nonlinear Schr?dinger equation
1
1978
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
A ˉ∂-dressing approach to the Kundu-Eckhaus equation
1
2021
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
The Riemann-Hilbert problem and long-time asymptotics for the Kundu-Eckhaus equation with decaying initial value
1
2018
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
A Riemann-Hilbert approachto a generalized nonlinear Schr?dinger equationon the quarter plane
1
2020
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions
1
2019
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
The Darboux transformation of the Kundu-Eckhaus equation
2
2018
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
... 它包含非线性光学中的五次非线性项和 Raman 效应, 其中 q=q(x,t) 是一个复光滑波包函数, 下标表示对变量的偏导数, β 是一个实常数. 据我们所知, 目前已经存在许多有关方程 (1.2) 畸形波解的研究. 例如, 在文献[35] 中利用广义 Darboux 变换结合规范变换已经研究了方程 (1.2) 的 N-阶畸形波解. 在文献 [42]中, 利用广义 Darboux 变换结合 Taylor 展开式构造了方程 (1.2) 的高阶畸形波解并考虑了五次非线性项对解的动力学行为的影响. 在文献[43]中, 首先利用广义 Darboux 变换的相关理论知识构造了方程 (1.2) 的畸形波解, 然后通过数值计算和图像分析, 证明了五次非线性项和 Raman 效应非线性项能够影响高阶畸形波中驼峰的空间分布, 但驼峰的振幅和出现时间不变. 在他们的论文中, 为了利用广义 Darboux 变换得到方程 (1.2) 的畸形波解, 一个关键的步骤就是需要计算一系列相应特征函数的复导数. 但是在本文的第三节我们引入了方程 (1.2) Lax 对的解族, 该解族可以用变量分离形式的指数矩阵表示. 因此, 相比于其它论文利用广义 Darboux 变换对畸形波解的研究, 本文在推导畸形波解的显式表达式的过程中没有任何的导数计算, 这为构造方程的畸形波解提供了便利. ...
Higher-order rogue wave solutions of the Kundu-Eckhaus equation
3
2014
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
... 它包含非线性光学中的五次非线性项和 Raman 效应, 其中 q=q(x,t) 是一个复光滑波包函数, 下标表示对变量的偏导数, β 是一个实常数. 据我们所知, 目前已经存在许多有关方程 (1.2) 畸形波解的研究. 例如, 在文献[35] 中利用广义 Darboux 变换结合规范变换已经研究了方程 (1.2) 的 N-阶畸形波解. 在文献 [42]中, 利用广义 Darboux 变换结合 Taylor 展开式构造了方程 (1.2) 的高阶畸形波解并考虑了五次非线性项对解的动力学行为的影响. 在文献[43]中, 首先利用广义 Darboux 变换的相关理论知识构造了方程 (1.2) 的畸形波解, 然后通过数值计算和图像分析, 证明了五次非线性项和 Raman 效应非线性项能够影响高阶畸形波中驼峰的空间分布, 但驼峰的振幅和出现时间不变. 在他们的论文中, 为了利用广义 Darboux 变换得到方程 (1.2) 的畸形波解, 一个关键的步骤就是需要计算一系列相应特征函数的复导数. 但是在本文的第三节我们引入了方程 (1.2) Lax 对的解族, 该解族可以用变量分离形式的指数矩阵表示. 因此, 相比于其它论文利用广义 Darboux 变换对畸形波解的研究, 本文在推导畸形波解的显式表达式的过程中没有任何的导数计算, 这为构造方程的畸形波解提供了便利. ...
... 似乎只考虑Lax对(5.2)来分析势函数 u(x,t) 就可以从方程 u(x,t) 中得到势函数 q(x,t). 但是该工作不同于文献[43-44,46], 这里研究方程 (1.2) 的畸形波直接从Lax对(2.1)开始而不是 Lax 对(5.2), 这是该工作的创新点之一. 贯穿本文所有的计算中, 不需要解决复杂的积分算子. ...
The n-fold Darboux transformation for the Kundu-Eckhaus equation and dynamics of the smooth positon solutions
2
2019
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
... 似乎只考虑Lax对(5.2)来分析势函数 u(x,t) 就可以从方程 u(x,t) 中得到势函数 q(x,t). 但是该工作不同于文献[43-44,46], 这里研究方程 (1.2) 的畸形波直接从Lax对(2.1)开始而不是 Lax 对(5.2), 这是该工作的创新点之一. 贯穿本文所有的计算中, 不需要解决复杂的积分算子. ...
Rogue waves of the Kundu-Eckhaus equation in a chaotic wave field
1
2016
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
Dynamics of breather waves and higher-order rogue waves in a coupled nonlinear Schr?dinger equation
2
2018
... 虽然方程 (1.1) 有广泛的物理应用, 但是为了更好的揭示高阶非线性效应在现实物理系统中的作用, 它是非常有必要在方程 (1.1) 中添加更多的相关项. 一个主要的研究是在非线性薛定谔方程 (1.1) 中增加高阶项和耗散项以便精确地描述某些系统中的非线性现象. 因此, 本文主要研究如下可以用来模拟波在色散介质中传播的聚焦 Kundu-Eckhaus 方程[35⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-46] ...
... 似乎只考虑Lax对(5.2)来分析势函数 u(x,t) 就可以从方程 u(x,t) 中得到势函数 q(x,t). 但是该工作不同于文献[43-44,46], 这里研究方程 (1.2) 的畸形波直接从Lax对(2.1)开始而不是 Lax 对(5.2), 这是该工作的创新点之一. 贯穿本文所有的计算中, 不需要解决复杂的积分算子. ...