1 引言
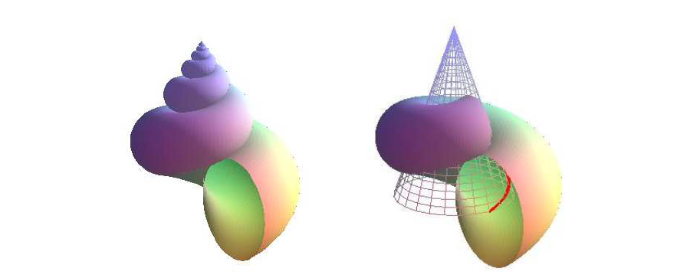
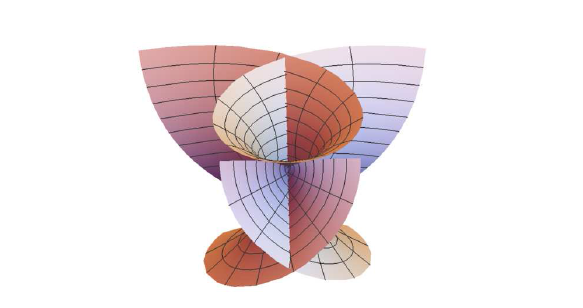
图 1
近些年来, 许多学者开始研究生物进化问题. 例如, Illert在实空间中描述了海洋贝壳的几何结构[7], 并将其理解为一类增长模型; Skalak 等人详细解释了增长曲面模型的运动学特征; Moulton和Goriely用某些生物体, 如贝壳和角的中心曲线构建了增长曲面的数学模型; Cowin, Hollister和Huiskes通过定义一个垂直于增长曲面的生长速度向量场来描述曲面增长的几何特征[8-9]. 后来, Illert和Reverberi等人将实空间中增长曲面的研究工作推广到了复空间, 他们结合物理学的运动规律, 利用复坐标讨论了贝壳、角、牙齿等生物结构的生成机制[10], 相关研究结果与欧氏空间相比十分简洁和美观. 为了深入探索和发现不同类型的生物结构, 尤其是它们的生成机制, 本文在三维复空间中定义并讨论由一类特殊的复曲线, 即迷向曲线, 生成的增长曲面的结构表达式, 将由迷向曲线演化而得到的增长曲面与迷向曲线的基本性质关联起来, 进而对增长曲面进行局部内在的描述.
2 预备知识
设
由曲线
在正则迷向曲线
这里
且
由方程组(2.1)可得到如下命题.
这里
2015年, 作者在[13]中定义了一个非常值解析函数, 类似Weierstrass表示, 给出了任意一条迷向曲线的参数表达式.
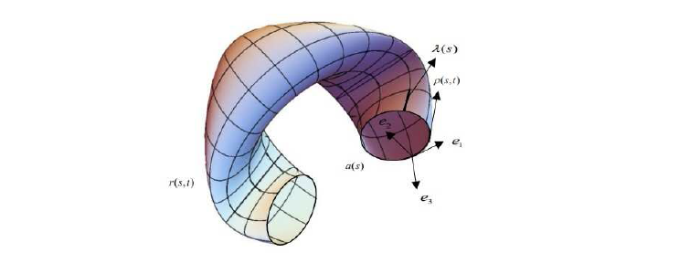
3 迷向增长曲面及其一般结构表达式
本节首先构造由迷向曲线生成的增长曲面, 然后研究该类增长曲面的一般结构表达式.
其中
其中
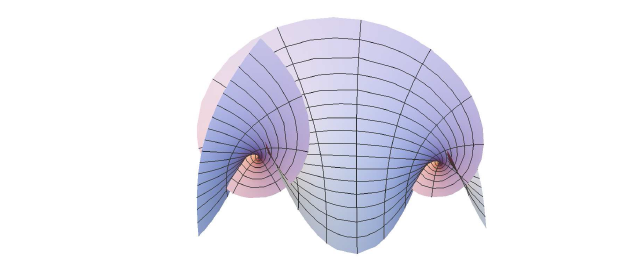
图 2
由命题2.1和命题2.2,
结合命题2.2和方程(3.1), 我们有下面的结论.
其中
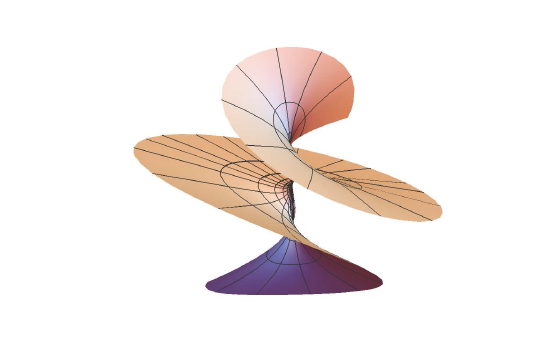
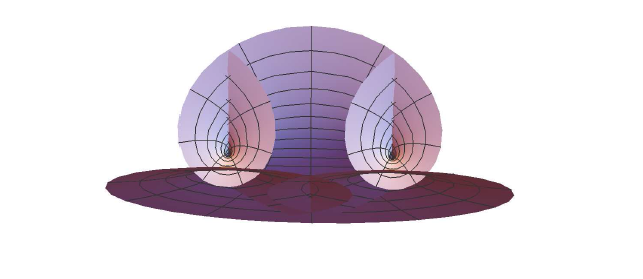
图 3
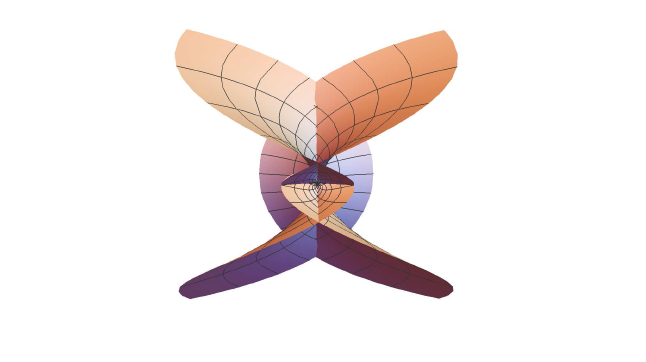
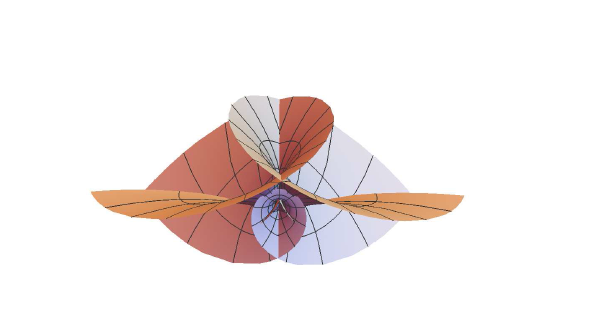
图4
4 由1 -型(3 -型)迷向螺线生成的迷向增长曲面的结构表达式
本节研究由
设
通过变量代换,
这里
解上述微分方程, 并经过适当的平移变换, 有下列三种情况.
情况 1 当
情况 2 当
情况 3 当
这里
根据以上3种情况,
则称它为1-3 -型(3-3 -型)迷向螺线. 这里
根据定理3.1和定义4.1, 可以得到下面的结论.
这里
图 5
图6
这里
图 7
图8
这里
图 9
图 10
5 由2 -型迷向螺线生成的迷向增长曲面的结构表达式
本节研究由
由命题2.2, 其结构函数满足
通过变量代换,
这里
解上述微分方程, 并经过适当的平移变换, 有下列三种情况.
情况 1 当
情况 2 当
情况 3 当
根据以上3种情况,
这里
根据定理3.1和定义5.1, 可以得到下面的结论.
这里
图 11
图 12
这里
图 13
图 14
这里
图 15
图 16
6 总结与展望
本文在三维复空间中, 利用迷向曲线的E. Cartan活动标架定义了迷向增长曲面的一般结构, 并根据生成迷向曲线的结构函数研究了此类增长曲面的类Weirstrass表达式. 考虑螺线在曲面增长中的重要地位和作用, 讨论了由三类迷向螺线生成的迷向增长曲面的一般结构表达式并给出相应的实例. 本文的研究属于复空间中迷向增长曲面的初始性工作, 所得结论可以为在复空间中讨论相关问题提供很好的研究思路和办法, 如复空间中迷向曲线流, 可积系统或孤立子方程等.
参考文献
Formation of the giant planets by concurrent accretion of solids and gas
DOI:10.1006/icar.1996.0190 URL [本文引用: 1]
Tree biomechanics: growth, cumulative prestresses, and reorientations
Continuum modeling and numerical simulation of cell motility
DOI:10.1007/s00285-011-0446-0
PMID:21710139
[本文引用: 1]

This work proposes a continuum-mechanical model of cell motility which accounts for the dynamics of motility-relevant protein species. For the special case of fish epidermal keratocytes, the stress and cell-substrate traction responses are postulated to depend on selected protein densities in accordance with the structural features of the cells. A one-dimensional version of the model is implemented using Arbitrary Lagrangian-Eulerian finite elements in conjunction with Lagrange multipliers for the treatment of kinematic constraints related to surface growth. Representative numerical tests demonstrate the capacity of the proposed model to simulate stationary and steady crawling states.
An analytical model for predicting residual stresses in progressively deposited coatings. Part 1: planar geometry
DOI:10.1016/S0040-6090(97)00199-5 URL [本文引用: 1]
On the geometrical forms of turbinated and discoid shells
Formulation and solution of the classical problem: II. Tubular three dimensional surfaces
DOI:10.1007/BF02451562 URL [本文引用: 1]
Bone stress adaptation models
DOI:10.1115/1.2895535
URL
[本文引用: 1]

The basic concepts employed in formulating models of the process of stress adaptation in living bone tissue are reviewed. A purpose of this review is to define and separate issues in the formulation of bone remodeling theories. After discussing the rationale and objective of these models, the concepts and techniques involved in the modeling process are reviewed one by one. It is concluded that some techniques will be more successful than others in achieving the goals of computational bone remodeling. In particular, rationale is given for the preference of surface bone remodeling approaches over internal bone remodeling approaches, and for interactive multi-scale level, rather than mono-scale level, computational strategies.
From structure to process, from organ to cell: recent developments of FE-analysis in orthopedic biomechanics
DOI:10.1115/1.2895534
URL
[本文引用: 1]

The introduction of finite element analysis (FEA) into orthopaedic biomechanics allowed continuum structural analysis of bone and bone-implant composites of complicated shapes (Huiskes and Chao, J. Biomechanics, Vol. 16, 1983, pp. 385–409). However, besides having complicated shapes, musculoskeletal tissues are hierarchical composites with multiple structural levels that adapt to their mechanical environment. Mechanical adaptation influences the success of many orthopaedic treatments, especiallly total joint replacements. Recent advances in FEA applications have begun to address questions concerning the optimality of bone structure, the processes of bone remodeling, the mechanics of soft hydrated tissues, and the mechanics of tissues down to the microstructural and cell levels. Advances in each of these areas, which have brought FEA from a continuum stress analysis tool to a tool which plays an ever-increasing role in the scientific understanding of tissue structure, adaptation, and the optimal design of orthopaedic implants, are reviewed.
Formulation and solution of the classical problem: I. Seashell geometry
Contributions to differential geometry of isotropic curves in the complex space {\Bbb C}^{3}-II
DOI:10.1016/j.jmaa.2016.02.072 URL [本文引用: 1]
Representations of rectifying isotropic curves and their centrodes in complex 3-space
DOI:10.3390/math9121451
URL
[本文引用: 1]

In this work, the rectifying isotropic curves are investigated in three-dimensional complex space C3. The conclusion that an isotropic curve is a rectifying curve if and only if its pseudo curvature is a linear function of its pseudo arc-length is achieved. Meanwhile, the rectifying isotropic curves are expressed by the Bessel functions explicitly. Last but not least, the centrodes of rectifying isotropic curves are explored in detail.
Some isotropic curves and representation in complex space
DOI:10.4134/BKMS.2015.52.3.963 URL [本文引用: 5]