1 引言
包虫病又称棘球蚴病, 是棘球绦虫在动物与人体内寄生导致的一类人畜共患寄生虫病, 该病不仅威胁人和牲畜的健康, 同时也严重影响着畜牧业的发展[1]. 棘球绦虫的生命周期主要包括三个阶段, 卵、幼虫、成虫. 成虫寄生在终末宿主(犬、狼和狐狸等)的小肠内, 成虫产生的虫卵随终末宿主的粪便排出体外, 污染草地、水源、家居环境或附着在动物的毛皮上. 当中间宿主(牛、羊、猪和田鼠等)接触并吞食虫卵后, 虫卵在其体内发育成棘球蚴. 受感染牲畜在被屠宰后内脏又被终末宿主吞食, 其中所含的棘球蚴又可在终末宿主的小肠内发育为成虫, 从而继续产生虫卵, 这样就造成了棘球蚴病的循环传播. 人类为意外吞食虫卵的偶然中间宿主[2].
关于包虫病的研究由来已久, 早在 1987 年, Roberts M G, Lawson J R 和 Gemmell M A 等人就利用动力学模型研究了包虫病在新西兰犬和羊之间的传播[6,7], 文章在一定程度上揭示了包虫病的传播机制. 接着很多国内外的学者开始从不同角度改进包虫病动力学模型. 文献[8]考虑了狗, 羊和环境中的虫卵三种生物之间的疾病传播情况; 文献[9]引入时滞因素, 建立了一类关于终末宿主和中间宿主的, 具有产卵期和成熟期两个时滞的传播动力学模型; 文献[10]更进一步, 建立了带有时滞影响的反应扩散方程, 并给出了无病平衡点和地方病平衡点全局渐近稳定的判别依据和模型具有行波解的条件; 文献[11] 则建立了一类随机环境波动的包虫病传播动力学模型.
2 模型的建立与分析
根据西藏地区实际流行情况与防控措施, 我们做如下假设说明.
(1)由于特殊文化背景, 西藏地区的流浪犬数量巨大, 因此我们仅考虑流浪犬为主要的终末宿主. 同时根据西藏不杀生的宗教信仰, 政府在疾病防治过程中针对流浪犬的主要措施为捕捉、集中圈养(下文称归置). 假设
另外, 流浪犬数量庞大而可获得的生存资源却很有限, 故假设其总量遵循 Logistic 增长规律, 满足如下方程
其中
(2)假设
(3)人类为误食虫卵的偶然中间宿主. 假设
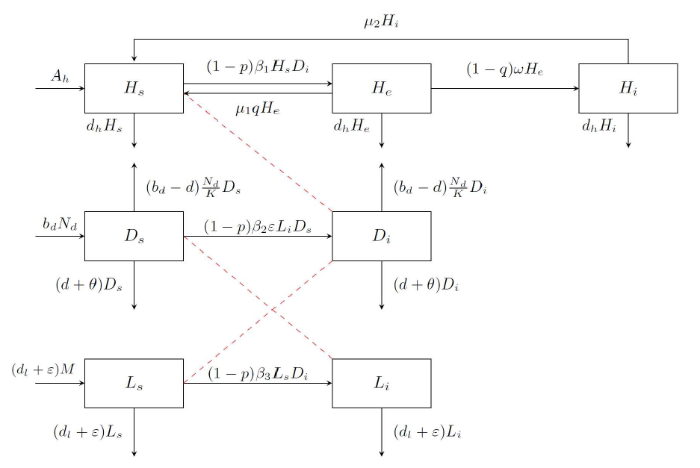
根据图1, 可建立如下动力学模型
图1
模型中的参数均为正值, 其中
根据问题的实际含义我们仅在区域
中讨论系统 (2.1) 解的性态. 并且容易验证
显然, 系统 (2.1) 总存在一个平凡平衡点
利用下一代矩阵的方法[16], 令
进一步, 当
3 平衡点的稳定性
定理3.1 平凡平衡点
证 系统 (2.1) 在
而
定理3.2 当
证 系统 (2.1) 在
显然, 该特征方程有五个实根且都小于零, 另外两个根为
所以当
下面证明当
由于
由极限系统的理论可知, 系统 (3.1) 平衡点的稳定性等价于系统 (3.2) 平衡点的稳定性. 所以现在问题转化为讨论系统 (3.2) 的平衡点 (0,0) 的全局稳定性.
设
将函数
则当
而
接下来考虑系统 (2.1) 前三个方程所构成的子系统
当
综上所述, 当
定理3.3 当
证 类似于上面的证明方法, 先考虑极限系统 (3.2) 的平衡点
选取
显然,
且等号仅在
接下来考虑子系统 (3.3). 当
显然, 系统 (3.4) 为一个线性系统, 其特征方程为
其中
由于
综上所述, 当
如图2 所示, 当取定参数, 使得
图2
4 模型的应用
在这一部分, 我们首先利用数据对模型的合理性进行检验, 其次结合模型模拟的结果, 对防控策略提出合理的建议和优化措施.
4.1 数值模拟
根据公开发表的文献和公共卫生科学数据中心统计的包虫病病例可知, 西藏自治区从 2004-2020 年全区共报告病例数 1474 例, 其中 2017 年病例数最多为 273 例. 而 2012-2016 年完成的包虫病流行病学调查则显示西藏地区的包虫病患病率高达 1.66%, 之后完成的关于包虫病的普查工作, 进一步精确了西藏地区包虫病的患病率为 0.91%, 即我们模型中的潜伏期患者
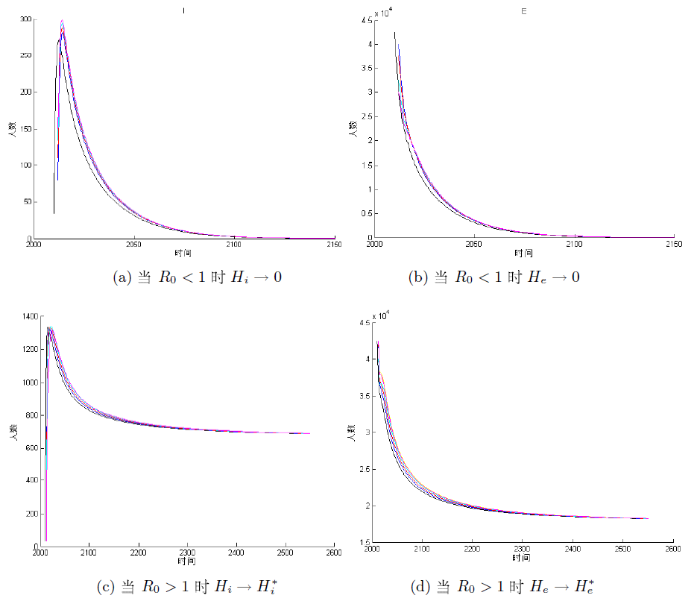
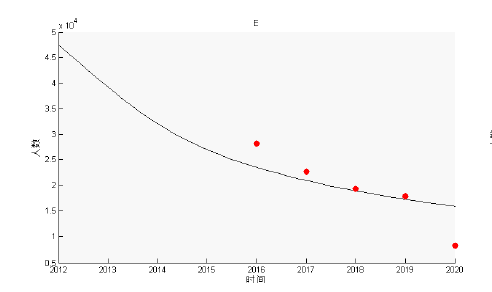
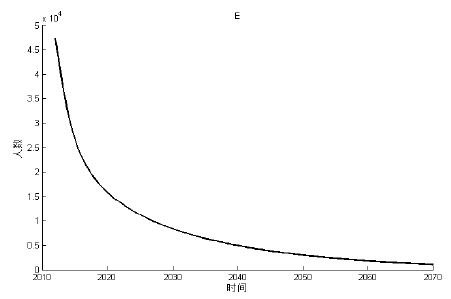
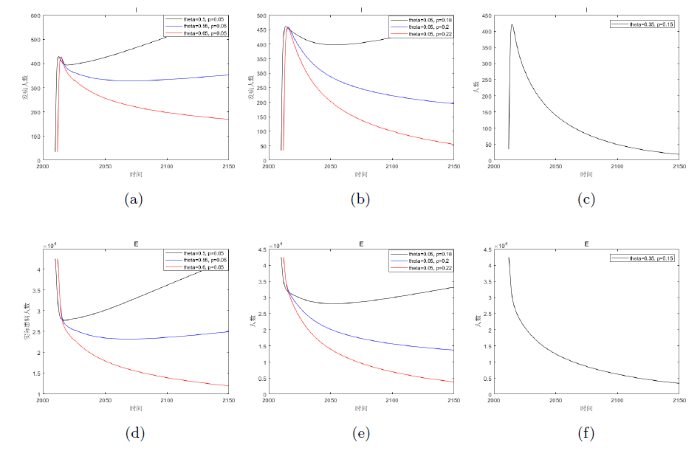
下面我们利用 2012 年的数据 H_{s}=3033666, H_{e}=42500, H_{i}=34, D_{s}=2.38\times105, D_{i}=7.2\times10^{4}, L_{s}=2.53\times10^{7}, L_{i}=3.683\times10^{6} 作为初始值条件进行计算. 其结果如图3-5 所示, 可以看出 H_{i} 在 2016 年左右会达到峰值, 之后便会下降, 并且最大值不超过 450 例, 整体的变化趋势与实际情况是一致的. 此外将 H_{e} 的模拟结果与文献[5]中西藏实际患病人数(见表1)比较可知, 除 2020 年的数据外, 另外四年的数据与模拟解之间匹配良好并且在稳步地减少. 这说明模型基本上符合当地的实际情况, 具有一定的合理性.
图3
图4
图5
4.2 防控策略讨论
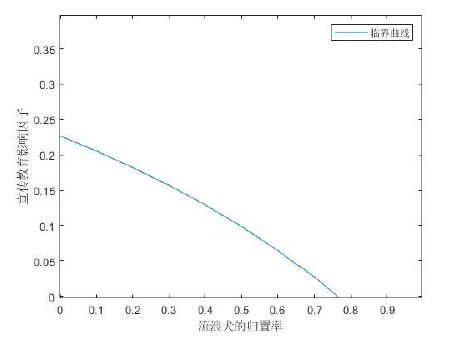
下面我们研究
即图6, 它刻画了宣传教育与流浪犬归置对基本再生数
图6
通过图像可知, 如果没有了平时的宣传教育, 即
图7
5 结论
本文根据包虫病的传播机理以及西藏地区的政策法规, 构建了一类符合西藏地区实际情况的包虫病动力学模型. 通过对模型的分析和应用, 发现当基本再生数
参考文献
Biological, epidemiological, and clinical aspects of echinococ-cosis, a zoonosis of increasing concern
DOI:10.1128/CMR.17.1.107-135.2004 URL [本文引用: 1]
The impact of globalisation on the distribution of Echinococcus multilocularis
DOI:10.1016/j.pt.2012.03.004
PMID:22542923
[本文引用: 1]

In the past three decades, Echinococcus multilocularis, the cause of human alveolar echinococcosis, has been reported in several new countries both in definitive hosts (canids) as well as in people. Unless treated, infection with this cestode in people is fatal. In previously endemic countries throughout the Northern Hemisphere, geographic ranges and human and animal prevalence levels seem to be increasing. Anthropogenic influences, including increased globalisation of animals and animal products, and altered human/animal interfaces are thought to play a vital role in the global emergence of this pathogenic cestode. Molecular epidemiological techniques are a useful tool for detecting and tracing introductions, and differentiating these from range expansions.Copyright © 2012 Elsevier Ltd. All rights reserved.
西藏自治区棘球蚴病病例分析
Analysis of hydatid disease cases in Tibet Autonomous Region
2004-2020年全国棘球蚴病疫情分析
The endemic status of echinococcosis in China from 2004 to 2020
2018-2019年全国棘球蚴病监测分析
Analysis of the results of echinococcosis surveillance in China from 2018 to 2019
Population dynamics in echinococcosis and cysticercosis: biological parameters of Echinococcus granulosus in dogs and sheep
DOI:10.1017/S0031182000065483
URL
[本文引用: 1]

The numerical distributions of Echinococcus granulosus in an experimental dog population are described. At all dose rates of protoscoleces from 10 to 175000 the distribution of worms was over-dispersed. Host age had no effect. There was a direct proportionality between the infective-stage density and rate of infection, and between the latter and the index of clumping. The worm burdens were significantly higher in the proximal than distal portions of the small intestine. Lengths of the 3- and 4-segmented worms increased from 4 to 10 and 4 to 8 weeks of age, respectively. Thereafter apolysis was asynchronous and could not be determined. Eggs were first detected in the faeces at 6 weeks and the mean age at oogenesis was 7·26 weeks. Retarded growth of the whole population of worms was observed in some dogs. For the first few infections, worm burdens varied widely in the same dog, but by the 6th infection 50% of the dog population had developed a relative insusceptibility to infection. Growth or oogenesis of the worms were not affected. A short-acting immune response was artificially induced in some dogs following the parenteral injection of activated embryos of E. granulosus, Taenia hydatigena, T. ovis, T. multiceps, T. pisiformis and T. serialis. The response affected either the number of worms established, growth or oogenesis or all three parameters. There was a strong positive correlation between numbers and lengths of worms in dogs with acquired and induced immunity, indicating that no ‘crowding’ effects were involved. In sheep populations the mean number of cysts which established was directly proportional to the number of eggs given, implying that there was no negative feedback mechanism operating at this stage of the life-cycle. The distribution of the larval population in sheep was over-dispersed and the index of clumping increased with the size of the egg dose from 25 to 2500 eggs. Protoscoleces were first observed in cysts at 2 years and the proportion producing them increased with age, with an estimate of 50% of cysts containing protoscoleces at 6 years. No deaths were observed in dogs or sheep even when high parasite burdens were present, implying that E. granulosus does not regulate the population of its hosts.
Population dynamics in echinococcosis and cysticercosis: mathematical model of the life-cycle of Echinococcus granulosus
DOI:10.1017/S0031182000065495
URL
[本文引用: 1]

A mathematical model of the life-cycle of Echinococcus granulosus in dogs and sheep in New Zealand is constructed and used to discuss previously published experimental and survey data. The model is then used to describe the dynamics of transmission of the parasite, and the means by which it may be destabilized. It is found that under the conditions that prevailed in New Zealand during the late 1950s, at the time of surveys of this parasite, the dog–sheep life-cycle was not regulated by any effective density-dependent constraint. In contrast there was evidence for an effective acquisition of immunity to reinfection by cattle. The long time to maturity of the cyst in sheep, together with the practice of feeding aged sheep to dogs, provides a time delay in the intermediate host. By comparison, the time to maturity of the adult stage in dogs is short, but it is of sufficient magnitude to be a key factor in the destabilization of the system by a regular dog-dosing programme. The model used to describe the life-cycle is a linear integrodifferential equation of the Volterra type. Such equations are intrinsically unstable in that a small perturbation in parameters can drive a previous equilibrium solution to zero. At the time of the surveys, the value of the basic reproductive rate, R0 was close to 1, and it has since been reduced below 1 by control measures.
一类具有饱和发生率的包虫病传播模型研究
A Echinococcosis model with saturation incidence
Global dynamics of a time-delayed echinococcosis transmission model
DOI:10.1186/s13662-014-0331-4 URL [本文引用: 1]
A spatial echinococcosis transmission model with time delays: stability and traveling waves
一类随机包虫病传播模型及CDC数据拟合
Modeling a stochastic Echinococcosis transmission and fitting the statistical data of CDC
Impact of disposing stray dogs on risk assessment and control of Echinococcosis in Inner Mongolia
DOI:S0025-5564(17)30436-4
PMID:29526551
[本文引用: 1]

Echinococcosis has been recognized as one of the most important helminth zoonosis in China. Available models always consider dogs as the mainly definitive hosts. However, such models ignore the distinctions between domestic dogs and stray dogs. In this study, we propose a 10-dimensional dynamic model distinguishing stray dogs from domestic dogs to explore the special role of stray dogs and potential effects of disposing stray dogs on the transmission of Echinococcosis. The basic reproduction number R, which measures the impact of both domestic dogs and stray dogs on the transmission, is determined to characterize the transmission dynamics. Global dynamic analysis of the model reveals that, without disposing the stray dogs, the Echinococcosis becomes endemic even the domestic dogs are controlled. Moreover, due to the difficulties in estimating the parameters involved in R with real data and the limitation of R in real-world applications, a new risk assessment tool called relative risk index I is defined for the control of zoonotic diseases, and the studies of the risk assessment for Echinococcosis infection show that it is essential to distinguish stray dogs from domestic dogs in applications.Copyright © 2018 Elsevier Inc. All rights reserved.
Modeling and analysis of the transmission of Echinococcosis with application to Xinjiang Uygur Autonomous Region of China
DOI:10.1016/j.jtbi.2013.04.020
PMID:23669505
[本文引用: 2]

Echinococcosis, which is one of the zoonotic diseases, can threaten human health and hinder the development of animal husbandry seriously. Especially in Xinjiang Uygur Autonomous Region of China, Echinococcosis is regarded as one of the most serious endemic diseases.The number of human Echinococcosis has increased dramatically in the last 10 years, partially due to poor understanding of the transmission dynamics of Echinococcosis and lack of effective control measures of the disease. In this paper, in order to explore effective control and prevention measures we propose a deterministic model to study the transmission dynamics of Echinococcosis in Xinjiang. The results show that the dynamics of the model is completely determined by the basic reproductive number R0. If R0<1, the disease-free equilibrium is globally asymptotically stable. When R0>1, the disease-free equilibrium is unstable, and the endemic equilibrium is globally asymptotically stable. Based on the data reported by Xinjiang Center for Disease Control and Prevention (Xinjiang CDC), the numerical simulation result matches Echinococcosis data well. The model provides an approximate estimate of the basic reproduction number R0=1.67. This indicates that Echinococcosis is endemic in Xinjiang with the current control measures. Finally, we perform some sensitivity analysis of several model parameters and give some useful comments on controlling the transmission of Echinococcosis. Copyright © 2013 Elsevier Ltd. All rights reserved.
新疆地区包虫病模型的建立与仿真
The Establishment and Simulation of Echinococcosis Model in Xinjiang
Modeling and analyzing the effects of fixed-time intervention on transmission dynamics of echinococcosis in Qinghai province
Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission
A precise definition of the basic reproduction number, R0, is presented for a general compartmental disease transmission model based on a system of ordinary differential equations. It is shown that, if R0<1, then the disease free equilibrium is locally asymptotically stable; whereas if R0>1, then it is unstable. Thus, R0 is a threshold parameter for the model. An analysis of the local centre manifold yields a simple criterion for the existence and stability of super- and sub-threshold endemic equilibria for R0 near one. This criterion, together with the definition of R0, is illustrated by treatment, multigroup, staged progression, multistrain and vector-host models and can be applied to more complex models. The results are significant for disease control.
我国西部地区农牧民包虫病防控认知情况及其影响因素
Awareness of herdsmen for the prevention and control of echinococcosis and potential risk factors in western china