1 引言
乙型肝炎病毒(HBV)可导致健康肝细胞感染进而引发肝脏疾病, 如肝炎, 肝硬化和肝癌等. 据世界卫生组织报告, 目前全世界慢性乙肝病毒感染者约有3.5 亿人, 其中我国有近1.3 亿人, 乙型肝炎是我国发病率最高且危害最大的传染病之一[1]. 基于HBV感染机制, Nowak等[2]首次提出了三维常微分方程的HBV 感染模型, 此后更多学者开始关注HBV 感染模型, 并考虑不同因素使得所建立的模型更加符合实际背景. Min等[3]指出用非线性发生率函数刻画病毒感染过程更加符合实际, 李喜玲等[4]建立了一类具有免疫时滞和非线性发生率函数的分数阶HBV感染模型,利用泛函微分方程、Caputo分数阶导数和Lyapunov稳定性理论对模型进行了稳定性分析.
事实上, HBV主要活动区域是肝脏, 且病毒颗粒在肝脏内是可以自由移动的.假设病毒的扩散服从Fickian扩散原理, 王开发等[5]建立了病毒颗粒具有空间依赖的HBV感染模型, 并研究了模型行波解的存在性, 且在此基础上建立了一类具有胞内时滞的HBV扩散模型[6], 并研究了模型的稳定性; 甘庆涛等[7]利用交叉迭代和Schauder 不动点理论, 深入分析文献[6]中所建模型行波解的存在性. 进一步考虑不同的非线性发生率函数, 如饱和反应函数[8], Beddington-DeAngelis反应函数[9,10]和一般发生率函数[11]等, 学者们建立并分析HBV扩散模型的动力学性态. 需要注意上述工作均假设病毒与健康肝细胞接触, 然后引起细胞感染. 但研究表明[12,13]: 感染肝细胞与健康肝细胞接触后, 通过病毒性突触、奈米管等向健康肝细胞内释放大量病毒, 进而引发健康肝细胞被感染, 这种感染方式被称为“细胞-细胞”感染. 杨翠兰等[14]建立并分析了一类具有细胞-细胞感染和时滞的病毒感染模型的全局稳定性. Sun等[15]分析了一类具有一般非线性发生率反应函数、细胞-细胞感染和时滞的HBV扩散模型的全局稳定性, 并结合Matlab数值模拟验证了理论结果.
本文将考虑病毒DNA核衣壳和细胞-细胞感染, 并考虑病毒DNA 核衣壳和病毒颗粒的自由扩散, 建立具有非线性发生率函数的HBV 扩散模型并对其进行研究.
2 模型建立
本文综合考虑病毒DNA核衣壳和细胞-细胞传播的影响, 建立了一类一般性的HBV扩散模型
上述反应-扩散系统(2.1)具有以下的初始条件
其中
系统(2.1)中
非线性一般发生率函数
假设2.1 (i) 对于所有的
(ii) 对于所有的
(iii) 对于所有
3 解的适定性
定义系统 (2.1)满足的向量空间为
定义线性算子
由文献[21]得, 算子
显然,
其中
其中
引理 3.1 对于任意
其中
证 显然, 算子
其中
结合文献[引理2.1]. 证毕.
定理 3.1 若初始条件
证 记
根据假设2.1, 可以得到对于所有的
选择充分小的
证毕.
为了证明系统(2.1)解的存在性, 现定义如下空间
其中
引理 3.2
证 假设
解上述微分不等式, 可以得到
进一步地, 可以得到
通过系统(3.4)可以构造下述系统
通过解微分方程, 对于任意的
由比较原理[23], 显然
同样地, 依据系统(3.6)构造下述系统
解得
应用比较原理[23],
由引理3.1和定理3.1, 对于任意的初始条件
对任意的
是系统(2.1)过初值
引理 3.3[24] 对于任意
证 系统(2.1)的无感染平衡点为
根据系统(3.8), 可将
由假设, 可以得到
因为
另一方面, 由
综上所述,
4 平衡点的存在性
由下一代矩阵法可以定义系统(2.1)的基本再生数
显然, 系统(2.1)总有一个无感染平衡态
定理 4.1 当
证 已知系统(2.1)的平衡态满足方程组
通过简要计算, 可以得到
由
在区间
根据假设2.1, 显然有
故
当
下面证明
假设
5 主要结论
在本章节, 我们将讨论无感染平衡态的局部以及全局稳定性, 并且证明系统 (2.1)的一致持续性和感染平衡态的全局稳定性.
令
5.1 E_0 的稳定性
定理5.1 若
证 系统(2.1)在
其中
显然,
将其代入(5.1)式得到
考虑到方程组(5.2)有非平凡解, 根据克拉默法则, (5.2)的系数行列式
其中
显然, 特征方程(5.3)有一个负实特征根. 由
根据Routh-Hurwitz判据, 当
显然, 我们有
定理5.2 当
证 定义一个Lyapunov泛函
对
根据高斯散度定理和齐次Neumann边界条件(2.3), 可以得到
由假设2.1, 得到
因此, 当
5.2 一致持续性
定义5.1 若具有初始条件
则称系统(2.1)在
定义
其中
引理5.1[22] 若
在
定理5.3 对于系统(2.1), 有下述的三条结论成立.
(I) 对于任意
(II) 当
(III) 若
证 (I) 假设
对(5.5)式积分, 则
因此, 当
(II) 首先证明对于任意
由引理5.1, 令
则系统(5.7)存在唯一正平衡态
接下来分三种情形证明不等式成立. 若
显然对于任意
其中
其中
若
由最大值原理和比较原理[23], 对于所有的
若
结合
由最大值原理和Hopf边界引理[23], 对所有的
(III) 根据文献[推论4.3.2],
是矩阵
由定理5.1, 当
由比较原理, 存在
故, 对所有的
可以得到下述的比较系统
令
由于对于任意给定的
根据比较原理, 可以得到
由
并且系统(2.1)的第一个方程渐近于系统
由渐近自治半流理论(见文献[推论4.3]), 得到
下证当
接下来, 构造一个新的系统
令
显然,
定理5.4 当
证 令
即对所有的
因此, 系统(2.1)是一致持续的.证毕.
5.3 E^* 的稳定性
本小节我们将通过构造Lyapunov函数证明当
假设5.1 非线性一般发生率函数
定理5.5 当
证 定义一个Lyapunov泛函
且平衡态满足以下等式
对
其中
使用齐次Neumann边界条件(2.3)和散度定理, 可以推出
同样地, 我们得到
故
最后根据假设2.1以及
因此
故, 当
6 数值模拟
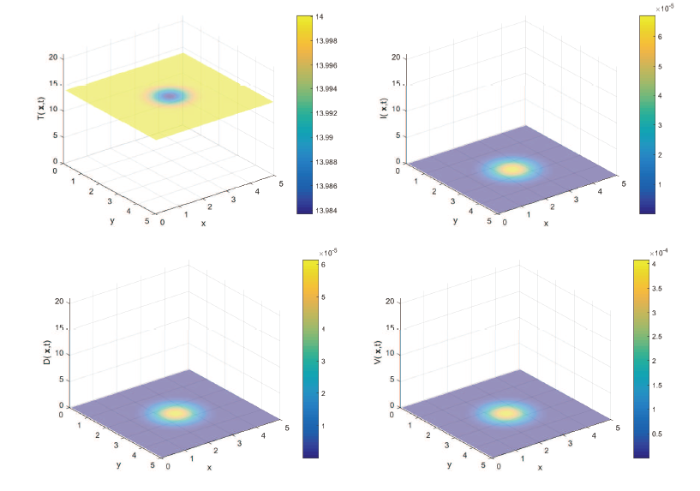
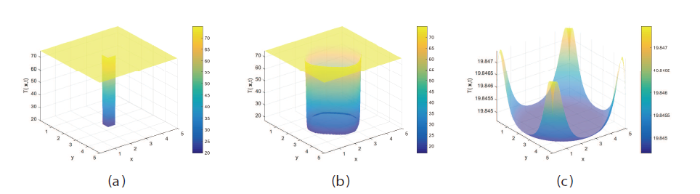
下面, 我们将通过数值模拟验证定理5.2和5.5 的正确性, 并探索扩散系数对HBV感染的影响. 取抽象函数
结合文献[1], 我们假设病毒的活动范围为有界区域
图1
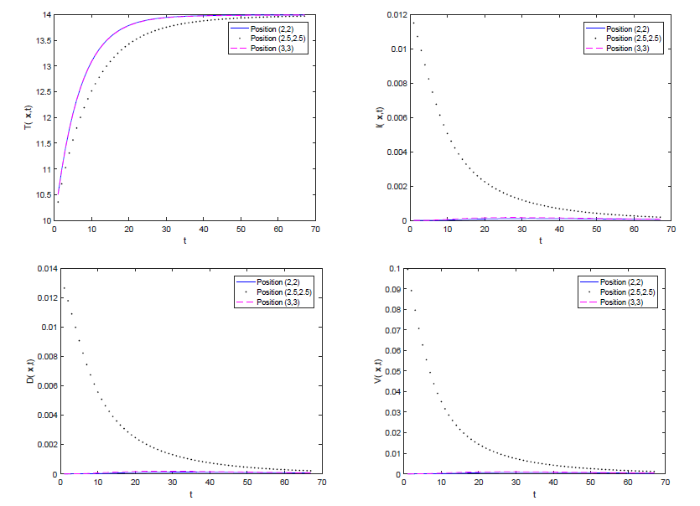
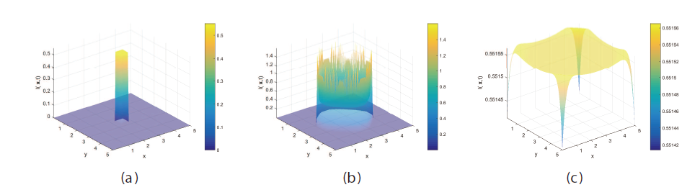
图2
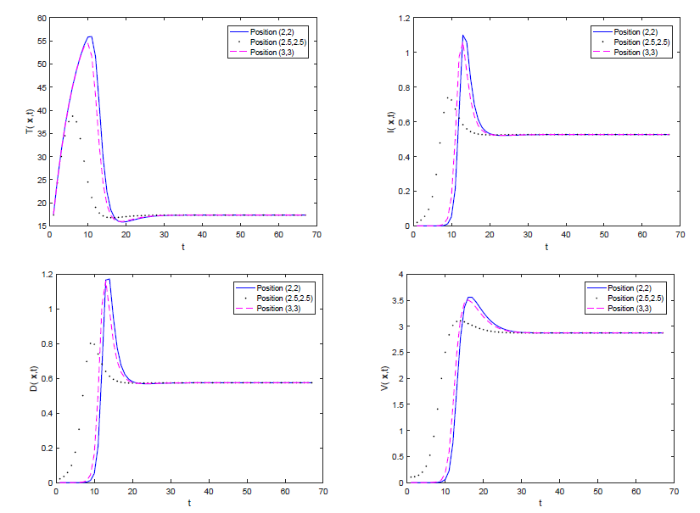
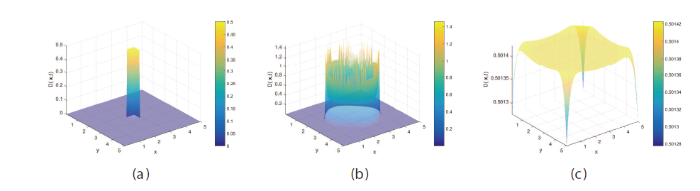
图3
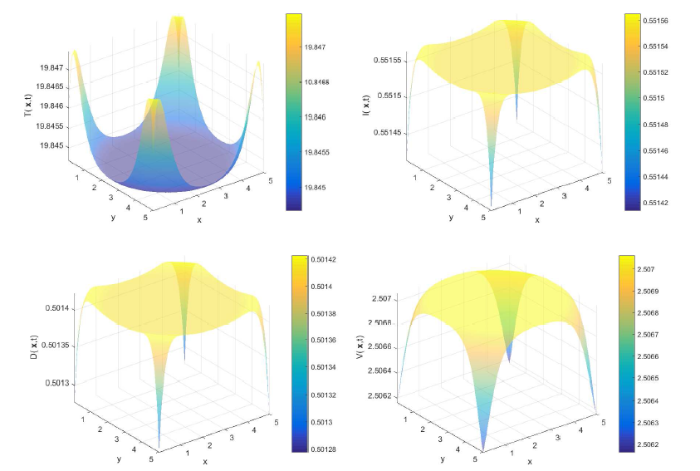
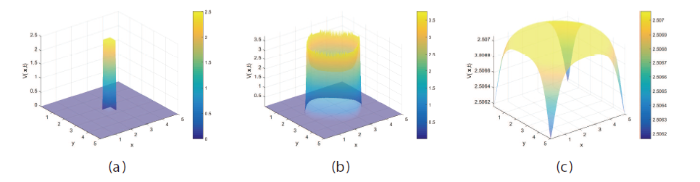
图4
图5
图5
取不同扩散系数时对状态变量
(a)
图6
图6
取不同扩散系数时对状态变量
(a)
图7
图7
取不同扩散系数时对状态变量
(a)
图8
图8
取不同扩散系数时对状态变量
(a)
7 结束语
本文建立了一类具有病毒DNA核衣壳和细胞间传播的一般HBV扩散模型,依据下一代矩阵法定义了模型的基本再生数, 证明了模型的一致持续性, 且证明了当
参考文献
The review of differential matrix models of HBV infection dynamics
DOI:10.1016/j.jviromet.2019.01.014 URL [本文引用: 2]
Viral dynamics in Hepatitis B virus infection
DOI:10.1073/pnas.93.9.4398
URL
[本文引用: 2]

Treatment of chronic hepatitis B virus (HBV) infections with the reverse transcriptase inhibitor lamivudine leads to a rapid decline in plasma viremia and provides estimates for crucial kinetic constants of HBV replication. We find that in persistently infected patients, HBV particles are cleared from the plasma with a half-life of approximately 1.0 day, which implies a 50% daily turnover of the free virus population. Total viral release into the periphery is approximately 10(11) virus particles per day. Although we have no direct measurement of the infected cell mass, we can estimate the turnover rate of these cells in two ways: (i) by comparing the rate of viral production before and after therapy or (ii) from the decline of hepatitis B antigen during treatment. These two independent methods give equivalent results: we find a wide distribution of half-lives for virus-producing cells, ranging from 10 to 100 days in different patients, which may reflect differences in rates of lysis of infected cells by immune responses. Our analysis provides a quantitative understanding of HBV replication dynamics in vivo and has implications for the optimal timing of drug treatment and immunotherapy in chronic HBV infection. This study also represents a comparison for recent findings on the dynamics of human immunodeficiency virus (HIV) infection. The total daily production of plasma virus is, on average, higher in chronic HBV carriers than in HIV-infected patients, but the half-life of virus-producing cells is much shorter in HIV. Most strikingly, there is no indication of drug resistance in HBV-infected patients treated for up to 24 weeks.
Mathematical analysis of a basic virus infection model with application to HBV infection
具有免疫时滞的分数阶 HBV 感染模型稳定性分析
Stability analysis of fractional-order hepatitis B virus infection model with immune delay
Propagation of HBV with spatial dependence
A mathematical model is proposed to simulate the hepatitis B virus (HBV) infection with spatial dependence. The existence of traveling waves is established via the geometric singular perturbation method. Numerical simulations show that the model admits non-monotone traveling profiles. Influences of various parameters on the minimum wave speed are also discussed.
Dynamics of an HBV model with diffusion and delay
In this paper we model and analyze the hepatitis B virus (HBV) infection in a diffusion model confined to a finite domain, induced by intracellular time delay between infection of a cell and production of new virus particles. The equilibrium solutions are obtained and the stability is analyzed if the space is assumed as homogeneous. When the space is inhomogeneous, the effects of diffusion and intracellular time delay are obtained by computer simulations.
Travelling waves of a hepatitis B virus infection model with spatial diffusion and time delay
DOI:10.1093/imamat/hxq009 URL [本文引用: 1]
An HBV model with diffusion and time delay
DOI:10.1016/j.jtbi.2009.01.001
PMID:19174169
[本文引用: 1]

In this paper, a hepatitis B virus (HBV) model with spatial diffusion and saturation response of the infection rate is investigated, in which the intracellular incubation period is modelled by a discrete time delay. By analyzing the corresponding characteristic equations, the local stability of an infected steady state and an uninfected steady state is discussed. By comparison arguments, it is proved that if the basic reproductive number is less than unity, the uninfected steady state is globally asymptotically stable. If the basic reproductive number is greater than unity, by successively modifying the coupled lower-upper solution pairs, sufficient conditions are obtained for the global stability of the infected steady state. Numerical simulations are carried out to illustrate the main results.
Dynamics of a diffusive HBV model with delayed Beddington-Deangelis response
DOI:10.1016/j.nonrwa.2013.06.005 URL [本文引用: 1]
一类具有扩散和Beddington-DeAngelis反应函数的病毒模型的全局稳定性
Global stability of a diffusive virus dynamics model with Beddington-DeAngelis incidence function
A generalized HBV model with diffusion and two delays
Viral clearance without destruction of infected cells during acute HBV infection
DOI:10.1126/science.284.5415.825
PMID:10221919
[本文引用: 1]

Viral clearance during hepatitis B virus (HBV) infection has been thought to reflect the destruction of infected hepatocytes by CD8(+) T lymphocytes. However, in this study, HBV DNA was shown to largely disappear from the liver and the blood of acutely infected chimpanzees long before the peak of T cell infiltration and most of the liver disease. These results demonstrate that noncytopathic antiviral mechanisms contribute to viral clearance during acute viral hepatitis by purging HBV replicative intermediates from the cytoplasm and covalently closed circular viral DNA from the nucleus of infected cells.
Modelling the impact of cell-to-cell transmission in hepatitis B virus
一个具有细胞-细胞传播和时滞的病毒动力学模型
A virus dynamical model with cell-to-cell viral transmission and delay
Dynamics of a diffusive virus model with general incidence function, cell-to-cell transmission and time delay
Chronic Hepatitis B infection and HBV DNA-containing capsids: modeling and analysis
DOI:10.1016/j.cnsns.2014.08.036 URL [本文引用: 1]
On an age-structured Hepatitis B virus infection model with HBV DNA-containing capsids
DOI:10.1007/s40840-020-01014-6 [本文引用: 1]
Dynamics of a diffusion-driven HBV infection model with capsids and time delay
Global stability of a diffusive and delayed HBV infection model with HBV DNA-containing capsids and general incidence rate
Spatiotemporal dynamics of a generalized HBV infection model with capsids and adaptive immunity
DOI:10.1007/s40819-019-0651-x [本文引用: 1]
A reaction-diffusion model for a deterministic diffusive epidemic
DOI:10.1016/0022-247X(81)90156-6 URL [本文引用: 1]
Analysis of a reaction-diffusion cholera model with distinct dispersal rates in the human population
DOI:10.1007/s10884-019-09820-8 [本文引用: 1]
Introduction to Functional Differential Equations
Robust persistence for semidynamical systems
DOI:10.1016/S0362-546X(01)00678-2 URL