1 引言
设
本文考虑如下的经典变分不等式问题, 记为 VI(
记
由于
参见文献[引理 2.1]. 在
最近,Ye[15] 给出了一种在
选取
其中
注意到惯性算法的生成点与解集的距离没有 Fejer 单调性. 因此, 当惯性系数为一个固定常数并且算法所生成的迭代点趋近于变分不等式的解时, 迭代点到变分不等式解集的距离会出现反复震荡的情形, 参见文献[21]. 因此, 本文中的惯性系数没有取常数, 而是把惯性系数修改为随着迭代步数单调递减趋于 0.
2 预备知识
本节中我们用
定义2.1 (i)若映射
则称
(ii)若映射
则称
(iii)若映射
则称
(iv)若存在常数
则称映射
引理2.1[22] 设
引理2.2[23] 对任意的
引理2.3[23] 设
(i) 对任意的
(ii) 序列
引理2.4[24] 设
那么有以下结论成立
(a)
(b) 存在一个
为了考虑变分不等式问题, 本文还做了如下假设
(A) 映射
(B)
(C) 映射
(D) 映射
(E) 集合
3 算法与收敛分析
在这一节里, 我们主要介绍算法及其收敛性分析. 我们先介绍算法如下.
算法 3.1 步骤1 选取初始点
步骤2 选取
步骤3
如果
步骤4
步骤5
步骤6 令
注3.1 注意到惯性算法的生成点与解集的距离没有 Fejer单调性. 因此, 本文的惯性系数
引理 3.1 设
证 见文献[引理 3.1].
引理 3.2 假设条件 (a), (b) 成立,
(a) 对于任意固定
(b)
证 (a)对于任意固定的
由
于是结合(3.6)式, 可以得到如下不等式关系
这里的第二个不等式的成立是依据
结合(3.7)式可知, 存在一个正整数
另一方面, 由 (3.2) 式中
结合(3.9)式通过变形可以得到, 对于任意的
在(3.1)式中, 根据
那么
最后由引理 2.4 以及 (3.11), (3.13) 式可以推出结论 (a) 成立. 下面证明结论 (b) 成立.
通过利用 (3.9), (3.10) 式可以观察到对于任意的
因此, 由结论 (a) 以及
再结合 (3.7) 和 (3.8) 式可得
接下来, 由 (3.4)式, 引理 3.1 以及
再由 (3.15)式, 则
此外, 通过利用 (3.15), (3.16)式, 以及三角不等式
可得
另外, 由(3.2)式中
那么
再由 (3.17)式,
最后, 利用(3.16),(3.18)式和三角不等式
引理 3.3 假设条件 (A)-(D) 成立,
证 由引理 3.2(a) 可知, 序列
情形1 当
情形2 当
那么对于任意固定的
由引理 3.1, 引理 3.2(b) 以及
当
这意味着存在一个正整数
再由
当
设
那么
取
则
由
这意味着
因此
下面说明
由此, 结合
即
由
引理 3.4 假设条件 (A)-(E) 成立,
证 设
情况1 若存在
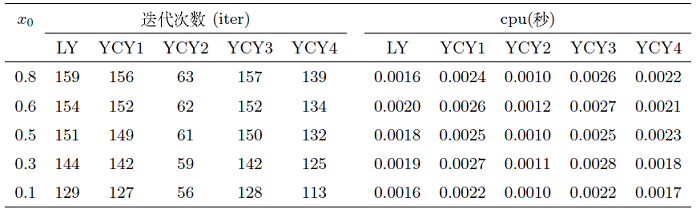
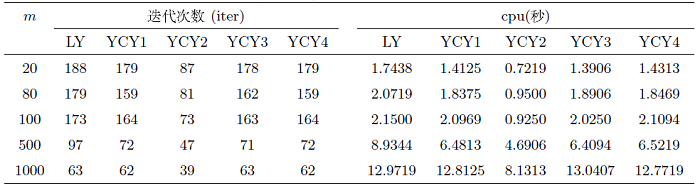
4 数值实验
YCY1:
YCY2:
YCY3:
YCY4:
YCY与 LY 的终止条件分别为
例4.1 本例被文献[14]用于拟单调变分不等式问题的算法检验. 设
例4.2 本例被文献[25] 用于单调变分不等式问题的算法检验. 设
这里的向量
例4.3 本例在
其中
因此, VI(
参考文献
Pseudo-monotone complementarity problems in Hilbert space
Convex programming in Hilbert space
DOI:10.1090/bull/1964-70-05 URL [本文引用: 1]
An extragradient method for finding saddle points and other problems
On a method for convex programs using asymmetrical modification of the Lagrange function
A modified forward-backward splitting method for maximal monotone mappings
DOI:10.1137/S0363012998338806 URL [本文引用: 2]
The subgradient extragradient method for solving variational inequalities in Hilbert Space
DOI:10.1007/s10957-010-9757-3 URL [本文引用: 1]
On the weak convergence of the extragradient method for solving pseudo-monotone variational Inequalities
DOI:10.1007/s10957-017-1214-0 [本文引用: 1]
求解伪单调变分不等式的修正投影收缩算法
Modified projection and contraction algorithm for solving pseudomonotone variational inequality problems
关于伪单调变分不等式与不动点问题的新投影算法
A new projection algorithm for solving pseudo-monotone variational inequality and fixed point problems
解变分不等式的一种二次投影算法
A double projection algorithm for solving variational inequalities
求解变分不等式的一种双投影算法
A double projection method for solving variational inequalities
A double projection method for solving variational inequalities without monotonicity
DOI:10.1007/s10589-014-9659-7 URL [本文引用: 3]
Solvability of the minty variational inequality
DOI:10.1007/s10957-017-1124-1 URL [本文引用: 1]
Weak convergence of iterative methods for solving quasimonotone variational inequalities
DOI:10.1007/s10589-020-00217-8 [本文引用: 10]
An infeasible projection type algorithm for nonmonotone variational inequalities
DOI:10.1007/s11075-021-01170-1 [本文引用: 1]
Some methods of speeding up the convergence of iteration methods
Inertial projection and contraction algorithms with larger step sizes for solving quasimonotone variational inequalities
DOI:10.1007/s10898-021-01083-2 [本文引用: 2]
New strong convergence theorem of the inertial projection and contraction method for variational inequality problems
一类伪单调变分不等式与不动点问题的自适应惯性投影算法
A Self-adaptive inertial projection algorithm for a class of pseudomonotone variational inequalities and fixed-point problems
A new inertial two-subgradient extragradient algorithm for variational inequality problems
Projection methods with alternating inertial steps for variational inequalities: Weak and linear convergence
DOI:10.1016/j.apnum.2020.06.009 URL [本文引用: 2]
Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert Space
DOI:10.1137/S1052623403427859 URL [本文引用: 1]
Modified hybrid projection methods for finding common solutions to variational inequality problems
DOI:10.1007/s10589-016-9857-6 URL [本文引用: 1]