1 引言
设
求解变分不等式问题的一个早期方法是超梯度方法. 更确切地说, Korpelevich[6] 提出了如下的双投影超梯度算法
这里
这里
他们证明了由此算法生成的序列
受上述事实的启发, 本文提出一个新的自适应次超梯度粘性算法并建立了强收敛定理, 通过数值例子说明了算法的有效性.
2 预备知识
用
任取
映射
若
映射
映射
为了证明主要定理, 需要如下引理.
引理2.1[18] 设
引理2.2[18] 设
(i)
(ii)
引理2.3[19] 设
存在实数
(i)
(ii) 存在
引理2.4[20] 设
(i) 任给
(ii)
引理2.5[21] 设
引理2.6[22] 设
如果
3 主要结果
为了证明所提出算法的收敛性, 我们先假设以下条件成立.
条件 1
条件 2 映射
条件 3
条件 4
现在引入下述算法.
注3.1 下述结果成立
由
引理3.1 由
证 由
若
于是由归纳法知
引理3.2 假设条件 1-3 成立. 设
证 因为
从而
注意到
于是
通过(3.4)和(3.5)式可得
因为
由
结合
将(3.9)式代入 (3.6)式得到
证毕.
类似于文献[引理 3.1]的证明, 我们有下述结果.
引理3.3 假设条件 1-3 成立. 设
定理3.1 假设条件 1-5 成立, 则由算法
证 首先证明
因为
由 (3.10) 式知
由
根据注 3.1, 有
结合 (3.11), (3.12) 和 (3.13) 式得
由
由数学归纳法得,
下面证明存在
根据 (3.14)式得
这里
这里
结合 (3.16) 和 (3.18) 式知
于是
这里
下面证明存在
由(3.11)和(3.12)式知
这里
下面证明
根据引理
为此, 首先假设
由(3.15)式得
于是有
从而
根据注 3.1 和条件 4 可得
由 (3.21), (3.22) 和 (3.23) 式得
因为
根据
再由 (3.24) 和 (3.26) 式知
因此, 结合注 3.1, (3.27), (3.19) 式和引理 2.6 可得
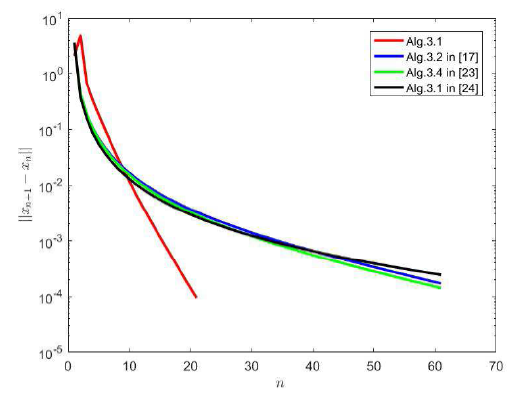
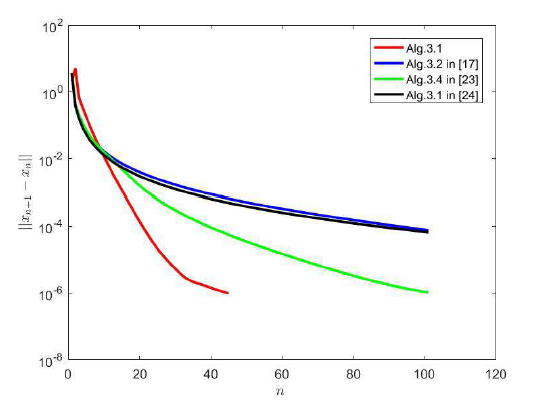
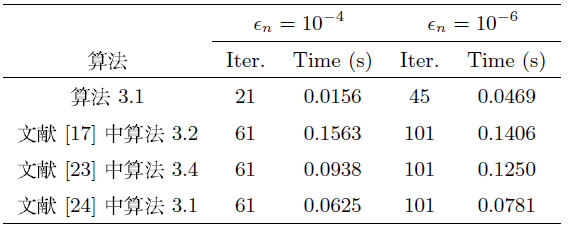
4 数值例子

图1
图2
例4.1 设
考虑
观察到
由此可知,
因此,
算法3.1:
文献[17]中算法 3.2:
文献[23]中算法 3.4:
文献[24]中算法 3.1:
参考文献
A multiprojection algorithms using Bregman projection in a product space
DOI:10.1007/BF02142692 URL [本文引用: 1]
The multiple-sets split feasibility problem and its applications for inverse problems
DOI:10.1088/0266-5611/21/6/017 URL [本文引用: 1]
Modified extragradient algorithms for solving equilibrium problems
DOI:10.1080/02331934.2018.1505886 URL [本文引用: 1]
The extragradient method for finding saddle points and other problems
The subgradient extragradient method for solving variational inequalities in Hilbert space
DOI:10.1007/s10957-010-9757-3 URL [本文引用: 1]
Extensions of Korpelevich extragradient method for variational inequality problem in Euclidean space
DOI:10.1080/02331934.2010.539689 URL [本文引用: 1]
Projected reflected gradient methods for monotone variational inequalities
DOI:10.1137/14097238X URL [本文引用: 1]
Modified subgradient extragradient method for variational inequality problems
DOI:10.1007/s11075-017-0452-4 [本文引用: 1]
A strong convergence theorem for Tseng's extragradient method for solving variational inequality problems
DOI:10.1007/s11590-019-01391-3 [本文引用: 1]
Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space
DOI:10.1080/10556788.2010.551536 URL [本文引用: 1]
Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces
DOI:10.1007/s10957-013-0494-2 URL [本文引用: 1]
Hybrid inertial proximal algorithm for the split variational inclusion problem in Hilbert spaces with applications
DOI:10.1080/02331934.2017.1306744 URL [本文引用: 1]
On inertial proximal algorithm for split variational inclusion problems
DOI:10.1080/02331934.2018.1486838 URL [本文引用: 1]
Viscosity approximation methods for solving fixed-point problems and split common fixed-point problems
DOI:10.1007/s11784-016-0323-y URL [本文引用: 1]
Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems
DOI:10.1007/s11590-019-01511-z [本文引用: 3]
An approximate inertial proximal method using enlargement of a maximal monotone operator
An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping
DOI:10.1023/A:1011253113155 URL [本文引用: 1]
Weak convergence of the sequence of successive approximations for nonexpansive mappings
DOI:10.1090/bull/1967-73-04 URL [本文引用: 1]
Pseudo-monotone complementarity problems in Hilbert space
DOI:10.1007/BF00941468 URL [本文引用: 1]
Approximation of zeros of inverse strongly monotone operators in Banach spaces
DOI:10.1016/j.na.2011.09.005 URL [本文引用: 1]
Improved inertial extragradient methods for solving pseudo-monotone variational inequalities
DOI:10.1080/02331934.2020.1808 [本文引用: 2]
A novel inertial projection and contraction method for solving pseudomonotone variational inequality problems
DOI:10.1007/s10440-019-00297-7
[本文引用: 2]

In this paper, we introduce a new algorithm which combines the inertial contraction projection method and the Mann-type method (Mann in Proc. Am. Math. Soc. 4:506-510, 1953) for solving monotone variational inequality problems in real Hilbert spaces. The strong convergence of our proposed algorithm is proved under some standard assumptions imposed on cost operators. Finally, we give some numerical experiments to illustrate the proposed algorithm and the main result.