Processing math: 0%

数学物理学报, 2023, 43(2): 570-580

两个带重启方向的改进 HS 型共轭梯度法

刘鹏杰,, 吴彦强,*, 邵枫, 张艳, 邵虎

中国矿业大学数学学院 江苏徐州 221116

Two Extended HS-type Conjugate Gradient Methods with Restart Directions

Liu Pengjie,, Wu Yanqiang,*, Shao Feng, Zhang Yan, Shao Hu

School of Mathematics, China University of Mining and Technology, Jiangsu Xuzhou 221116

通讯作者: *吴彦强，E-mail:wyq1976819@126.com

收稿日期: 2022-02-11   修回日期: 2022-10-17  

基金资助: 国家自然科学基金(72071202)
中央高校基本科研业务费专项资金(2017XKQY090)
江苏省研究生科研与实践创新计划(KYCX22_2491)
中国矿业大学研究生创新计划(2022WLKXJ021)
和中国矿业大学数学研究项目(2022DLZD04-203)

Received: 2022-02-11   Revised: 2022-10-17  

Fund supported: National Natural Science Foundation of China(72071202)
Fundamental Research Funds for the Central Universities(2017XKQY090)
Postgraduate Research & Practice Innovation Program of Jiangsu Province(KYCX22_2491)
Graduate Innovation Program of China University of Mining and Technology(2022WLKXJ021)
Teaching and Research Project of CUMT(2022DLZD04-203)

作者简介 About authors

刘鹏杰，E-mail:liupengjie2019@163.com

摘要

共轭梯度法是求解大规模无约束优化的有效方法之一. 该文首先对 Hestenes-Stiefel (HS) 共轭参数改进,再通过引入重启条件及重启方向, 建立两个带重启方向的改进 HS 型共轭梯度法. 第一个方法在弱 Wolfe 线搜索下产生下降方向, 第二个方法独立于任何线搜索得到充分下降性. 常规假设下, 分析并获得两个新方法的全局收敛性. 最后, 数值比对试验结果及性能图显示新方法是有效的.

关键词： 无约束优化; 共轭梯度法; 重启方向; 弱 Wolfe 线搜索; 全局收敛性

Abstract

The conjugate gradient method is one of the effective methods to solve large-scale unconstrained optimization. In this paper, the Hestenes-Stiefel (HS) conjugate parameter is improved, and then two extended HS-type conjugate gradient methods with restart directions are established by introducing restart conditions and restart directions. The first method produces descent direction under the weak Wolfe line search, and the second one obtains sufficient descent independent of any line search. Under conventional assumptions, the global convergence results of the two proposed methods are analyzed and obtained. Finally, the numerical comparison results and performance graphs show the effectiveness of the new methods.

Keywords： Unconstrained optimization; Conjugate gradient method; Restart direction; Weak Wolfe line search; Global convergence

PDF (408KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘鹏杰, 吴彦强, 邵枫, 张艳, 邵虎. 两个带重启方向的改进 HS 型共轭梯度法[J]. 数学物理学报, 2023, 43(2): 570-580

Liu Pengjie, Wu Yanqiang, Shao Feng, Zhang Yan, Shao Hu. Two Extended HS-type Conjugate Gradient Methods with Restart Directions[J]. Acta Mathematica Scientia, 2023, 43(2): 570-580

1 引言

考虑如下无约束优化问题

min
(1.1)

其中函数 f 在 {\mathbb R}^n 上连续可微. 共轭梯度法是求解问题 (1.1) 的一种有效方法, 记 g_k=\nabla f(x_k), 则对当前迭代点 x_k, 产生 x_{k+1} 的一般形式为

\begin{matrix} x_{k+1}=x_k+\alpha_k d_k, \end{matrix}
(1.2)
d_k= \begin{cases}-g_k, & k=1\, \\ -g_k+\beta_kd_{k-1}, & k\geq 2,\end{cases}
(1.3)

其中 \alpha_k 为某一线搜索产生的步长, 不同搜索方向 d_k 由共轭参数 \beta_k 决定. 经典共轭参数包括[1⇓⇓⇓-5]

\beta_k^{\rm HS}=\frac{g_k^{\top}y_{k-1}}{d_{k-1}^{\top}y_{k-1}}, \ \beta_k^{\rm FR}=\frac{\|g_k\|^2}{\|g_{k-1}\|^2}, \ \beta_k^{\rm PRP}=\frac{g_k^{\top}y_{k-1}}{\|g_{k-1}\|^2}, \ \beta_k^{\rm DY}=\frac{\|g_k\|^2}{d_{k-1}^{\top}y_{k-1}},

其中 y_{k-1}= g_k-g_{k-1}. 由此产生的四种著名共轭梯度法分别称为 Hestenes-Stiefel (HS) 方法, Fletcher-Reeves (FR) 方法, Polak-Ribière-Polyak (PRP) 方法和 Dai-Yuan (DY) 方法. 若问题 (1.1) 目标函数严格凸, 且采用精确线搜索计算步长, 上述四种方法等价. 对一般函数或使用非精确线搜索时, 上述方法存在较大差异. 一般情况下, HS 方法和 PRP 方法有良好数值性能, 却无法获得收敛性; FR 方法和 DY 方法有较好理论收敛性, 然而其数值效果难及 HS 方法和 PRP 方法. 特别地, HS 方法和 PRP 方法之所以具有较好数值表现, 可能是其求解于一般函数时自带重启性能.

近些年, 为寻求数值效果好且有收敛性的共轭梯度法, 许多学者对上述四种著名方法进行改进. 例如, 为取得 HS 方法理论上的相关性质, Yao 等[6] 给出一个改进 \beta_k^{\rm HS} 的共轭参数

\beta_k^{YWH}=\frac{\|g_{k}\|^2-\frac{\|g_{k}\|}{\|g_{k-1}\|}g_{k}^{\top} g_{k-1}}{d_{k-1}^{\top}y_{k-1}}.

结果表明, 强 Wolfe 线搜索下对应的 YWH 方法能产生下降方向并具有全局收敛性. Zhang[7]对 YWH 方法稍作调整, 有

\beta_k^{NHS}=\frac{\|g_{k}\|^2-\frac{\|g_{k}\|}{\|g_{k-1}\|} |g_{k}^{\top} g_{k-1}|}{d_{k-1}^{\top} y_{k-1}}.

上述 NHS 方法不仅像 HS 方法具有良好计算效果, 且和 DY 方法一样使用弱 Wolfe 线搜索有其下降性与收敛性. 基于文献[6,7], 江等[8]给出另一种改进 \beta_k^{ HS} 的版本, 即

\beta_k^{JMJ}=\frac{\|g_{k}\|^2-\frac{\|g_{k}\|}{\|d_{k-1}\|} |g_{k}^{\top} d_{k-1}|}{d_{k-1}^{\top} y_{k-1}}.

最近, Zhu 等[9]借助重启条件, 引入如下两个共轭参数

\beta_k^{\mathrm{DDY} 1}=\left\{\begin{array}{l}\frac{g_k^{\top}\left(g_k-\frac{\nu_1\left(g_k^{\top} d_{k-1}\right)^2}{\left\|g_k\right\|\|\| g_{k-1}\|\| d_{k-1} \|^2} g_{k-1}\right)}{d_{k-1}^{\top} y_{k-1}}, g_k^{\top} g_{k-1} \geq 0, \\\frac{g_k^{\top}\left(g_k+\frac{\nu_1\left(g_k^{\top} d_{k-1}\right)^2}{\left\|g_k\right\|\|\| g_{k-1}\|\| d_{k-1} \|^2} g_{k-1}\right)}{d_{k-1}^{\top} y_{k-1}}, g_k^{\top} g_{k-1}<0\end{array}\right.

和

\beta_k^{\mathrm{DDY} 2}= \begin{cases}\frac{g_k^{\top}\left(g_k-\frac{g_k^{\top} d_{k-1}}{\left\|d_{k-1}\right\|^2} d_{k-1}\right)}{d_{k-1}^{\top} y_{k-1}+\nu_2 g_k^{\top} d_{k-1}}, & g_k^{\top} d_{k-1} \geq 0 \\ 0, & g_k^{\top} d_{k-1}<0\end{cases}

其中扰动参数 \nu_{1} \in [01], \nu_{2} > 0. 弱 Wolfe 线搜索条件下\!, DDY1 方法和 DDY2 方法具有很好的数值性能表现, 且获得全局收敛性. 更多数值高效且收敛的改进共轭梯度法\!, 参见[10⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-23]及相关参考文献.

启发于文献[6,8], 本文首先给出一个改进 \beta_k^{HS} 的新共轭参数

\beta_k^{ EHS}=\frac{\|g_{k}\|^2-\frac{\|g_{k}\|}{\|y_{k-1}\|}g_{k}^{\top} y_{k-1}}{d_{k-1}^{\top}y_{k-1}}=\frac{\left(1- \frac{\|g_{k}\|}{\|y_{k-1}\|} \right)\|g_{k}\|^2 + \frac{\|g_{k}\|}{\|y_{k-1}\|}g_{k}^{\top} g_{k-1}}{d_{k-1}^{\top}y_{k-1}},

其形式上亦可视为 \|g_{k}\|^2 与 g_{k}^{\top} g_{k-1} 的仿射组合. 然而类似于 YWH 方法, 由 \beta_k^{\rm EHS} 和搜索方向 (1.3) 产生的 EHS 方法并未完全继承 DY 方法的优良理论特性. 例如, 在常用非精确弱 Wolfe 线搜索条件下, 即步长 \alpha_k 满足

\begin{matrix}\left\{\begin{array}{ll}f(x_k+\alpha_k d_k)\leq f(x_k)+\delta \alpha_k g_k^{\top} d_k,\\g(x_k+\alpha_k d_k)^{\top} d_k\geq \sigma g_k^{\top} d_k, \end{array}\right.\end{matrix}
(1.4)

其中 0<\delta < \sigma<1, DY 方法具有下降性和全局收敛性, 而 YWH 方法和 EHS 方法不一定有. 基于上述分析, 该文拟借鉴文献[9] 的重启条件及文献[10,11]的重启方向, 对上述 EHS 方法改进, 使其有与 DY 方法类似的良好理论性质, 同时亦继承 HS 方法较好的数值计算表现. 为此, 基于方向 (1.3)和参数 \beta_k^{\rm EHS}, 构造如下两个新的搜索方向

EHS-RD1 搜索方向.

d_k= \begin{cases}-g_k, & k \in M_1=\{k \mid k=1\}, \\ -g_k+\beta_k^{\mathrm{EHS} 1} d_{k-1}, & k \in M_2=\left\{k \mid k \geq 2, g_k^{\top} y_{k-1} \geq 0\right\}, \\ -g_k+\xi_1 \frac{g_k^{\top} g_{k-1}}{\left\|g_{k-1}\right\|^2} g_{k-1}, & k \in M_3=\left\{k \mid k \geq 2, g_k^{\top} y_{k-1}<0\right\},\end{cases}
(1.5)

其中参数 \xi_1 \in [0,1) 且

\beta_k^{\rm EHS1}=\frac{\|g_k\|^2-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top} y_{k-1}}{d_{k-1}^{\top}y_{k-1}}, \ \mu_{1} \in [01].
(1.6)

搜索方向.

d_k= \begin{cases}-g_k, & k \in N_1=\{k \mid k=1\}, \\ -g_k+\beta_k^{\mathrm{EHS} 2} d_{k-1}, & k \in N_2=\left\{k \mid k \geq 2, g_k^{\top} d_{k-1} \geq 0\right\}, \\ -g_k+\xi_2 \frac{g_k^{\top} d_{k-1}}{\left\|d_{k-1}\right\|^2} d_{k-1}, &k \in N_3=\left\{k \mid k \geq 2, g_k^{\top} d_{k-1}<0\right\},\end{cases}
(1.7)

其中参数 \xi_2 \in [0,1) 及

\beta_k^{\rm EHS2}=\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}}, \ \mu_{2} > 0.
(1.8)

为简便, 在弱 Wolfe 线搜索 (1.4) 产生步长 \alpha_k 前提下, 由 (1.2), (1.5)和 (1.6) 式建立的共轭梯度法记为 EHS-RD1 方法; 由 (1.2), (1.7)和 (1.8) 式建立的共轭梯度法记为EHS-RD2 方法.

下面给出共轭梯度法收敛性分析中常用假设 (A1)-(A2) 及 Zoutendijk 条件[24].

(A1) f(x) 在水平集 \Lambda=\{x\in {\mathbb R}^n\ | \ f(x)\leq f(x_1)\} 上有下界, 其中 x_1 为计算初始点.

(A2) f(x) 在 \Lambda 的一个邻域 \Delta 内可微, 且其梯度 g(x) 满足 Lipschitz 条件,即对任意 x,\bar{x}\in \Delta, 存在 L>0 使得 \|g(x)-g(\bar{x})\|\leq L\|x-\bar{x}\|.

引理1.1[24] 设假设 (A1)-(A2) 成立, 考虑迭代点 x_{k+1}=x_{k}+\alpha_{k}d_{k}, 步长 \alpha_k 由弱 Wolfe 线搜索 (1.4) 式产生. 若搜索方向 d_k 满足下降条件 g_{k}^{\top} d_{k}<0, 则 \sum\limits_{k=1}^{\infty}\frac{(g_{k}^{\top} d_{k})^2}{\|d_{k}\|^2}< \infty.

证 根据弱 Wolfe 线搜索 (1.4) 第一个不等式, 搜索方向的下降条件及假设 (A1) 知, 数列 \{f(x_k)\} 单调下降并有下界, 故其收敛.另一方面, 由假设 (A2), 得

(g_{k+1}-g_{k})^{\top} d_{k}\leq\|g_{k+1}-g_{k}\| \|d_{k}\|\leq L\|x_{k+1}-x_{k}\| \|d_{k}\|=L\alpha_{k} \|d_{k}\|^2,

此联立线搜索 (1.4) 第二个不等式, 有

\alpha_{k}\geq\frac{\sigma-1}{L} \frac{g_{k}^{\top} d_{k}}{\|d_{k}\|^2}.

上式结合线搜索 (1.4) 第一个不等式, 得

f(x_{k})-f(x_{k+1})\geq-\delta \alpha_kg_{k}^{\top} d_{k}\geq\frac{\delta(1- \sigma)}{L} \frac{(g_{k}^{\top} d_{k})^2}{\|d_{k}\|^2} \triangleq \Theta \frac{(g_{k}^{\top} d_{k})^2}{\|d_{k}\|^2},

其中 \Theta=\frac{\delta(1- \sigma)}{L} > 0. 再考虑到 \{f(x_k)\} 的收敛性, 有

\lim\limits_{q \rightarrow \infty}\bigg(\sum_{k=1}^{q}\frac{(g_{k}^{\top} d_{k})^2}{\|d_{k}\|^2} \bigg) \leq \lim\limits_{q \rightarrow \infty} \bigg(\sum_{k=1}^{q} \frac{1}{\theta} \big(f(x_{k})-f(x_{k+1})\big)\bigg) = \frac{1}{\theta}\big( f(x_1)- \lim\limits_{q \rightarrow \infty} f(x_{q+1})\big) < \infty,

从而结论成立.

该文其余部分组织如下: 第 2 节和第 3 节分别给出 EHS-RD1 方法和 EHS-RD2 方法的下降性及收敛性结果; 第 4 节使用无约束优化问题进行模拟测试, 以验证 EHS-RD1 方法和 EHS-RD2 方法的数值有效性.

2 EHS-RD1 方法

引理2.1 由 EHS-RD1 方法产生的搜索方向有下降性. 并且当 k\in M_{2}, 有

\begin{matrix}0 \leq \beta_k^{\rm EHS1}\leq\frac{g_{k}^{\top}d_{k}}{g_{k-1}^{\top}d_{k-1}}.\end{matrix}
(2.1)

证 数学归纳法. 当 k\in M_{1}, 有 g_1^{\top} d_1=-\|g_1\|^2<0.当 k \geq 2 时, 假设 g_{k-1}^{\top}d_{k-1}<0, 下面分两种情形证 g_{k}^{\top}d_{k}<0 成立.

(i) 当 k\in M_{2}, 有 g_{k}^{\top}y_{k-1} = \|g_{k}\| \cdot \|y_{k-1}\| \cos\theta_{k} \geq0 (\theta_{k} 为 g_k 与 y_{k-1} 的夹角), 则 \cos\theta_{k} \in [01]. 另一方面, 由 (1.4) 式第二个不等式知 d_{k-1}^{\top}y_{k-1} \geq(\sigma-1)g_{k-1}^{\top}d_{k-1}>0,从而

\beta_k^{\rm EHS1}=\frac{\|g_k\|^2-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top} y_{k-1}}{d_{k-1}^{\top}y_{k-1}} =\frac{\|g_k\|^2(1-\mu_1 \cos\theta_{k})}{d_{k-1}^{\top}y_{k-1}} \geq 0.
(2.2)

因此

\begin{matrix}g_k^{\top}d_k&=&-\|g_k\|^2+\beta_k^{\rm EHS1}g_k^{\top}d_{k-1}=-\|g_k\|^2+\frac{\|g_k\|^2-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top}y_{k-1}}{d_{k-1}^{\top}y_{k-1}}g_k^{\top}d_{k-1}\\&=&-\|g_k\|^2+\frac{\|g_k\|^2-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top}y_{k-1}}{d_{k-1}^{\top}y_{k-1}}d_{k-1}^{\top}y_{k-1}+\frac{\|g_k\|^2-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top}y_{k-1}}{d_{k-1}^{\top}y_{k-1}}g_{k-1}^{\top}d_{k-1}\\&=&-\mu_1\frac{\|g_k\|}{\|y_{k-1}\|}g_{k}^{\top}y_{k-1}+\beta_k^{\rm EHS1}g_{k-1}^{\top}d_{k-1}.\end{matrix}

上式联立 g_k^{\top}y_{k-1}\geq0, g_{k-1}^{\top}d_{k-1}<0 和 (2.2)式,有 g_k^{\top}d_k<0 且 0 \leq \beta_k^{\rm EHS1}\leq\frac{g_{k}^{\top}d_{k}}{g_{k-1}^{\top}d_{k-1}}.

(ii) 若 k\in M_{3}, 结合 \xi_1 \in [0,1), 则

g_k^{\top}d_k=-\|g_k\|^2+\xi_1\frac{(g_k^{\top}g_{k-1})^2}{\|g_{k-1}\|^2}\leq-(1-\xi_1)\|g_k\|^2<0.

证毕.

定理2.1 设假设 (A1)-(A2) 成立, 迭代点 \{x_{k}\} 由 EHS-RD1 方法产生, 则

\liminf\limits_{k\rightarrow\infty} \|g_k\|=0.

证 反证法, 设结论不成立, 则存在 \lambda>0, 使得 \|g_k\|^2\geq\lambda.

(i) 若 k\in M_{1}, 有 d_1=-g_1, 从而 \frac{\|d_1\|^2}{(g_1^{\top}d_1)^2}=\frac{1}{\|g_1\|^2}.

(ii) 若 k\in M_{2}, 则 d_k+ g_k= \beta_k^{\rm EHS1}d_{k-1}, 两边同时平方并移项, 有

\|d_k\|^2=(\beta_k^{\rm EHS1})^2\|d_{k-1}\|^2-2g_k^{\top}d_k-\|g_k\|^2.

两边再同除以 (g_k^{\top}d_k)^2, 结合 (2.1) 式得

\begin{matrix}\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}&=&\frac{(\beta_k^{\rm EHS1})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}-\frac{2}{g_k^{\top}d_k}-\frac{\|g_k\|^2}{(g_k^{\top}d_k)^2}\\&=&\frac{(\beta_k^{\rm EHS1})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}+\frac{1}{\|g_k\|^2}-(\frac{1}{\|g_k\|}+\frac{\|g_k\|}{g_k^{\top}d_k})^2\\&\leq&\frac{(\beta_k^{{\rm EHS1}})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}+\frac{1}{\|g_k\|^2}\\&\leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\frac{1}{\|g_k\|^2}.\end{matrix}

(iii) 若 k\in M_{3}, 则 d_k=-g_k+\xi_1\frac{g_k^{\top}g_{k-1}}{\|g_{k-1}\|^2}g_{k-1}, \xi_1 \in [0,1), 进一步有

\begin{matrix}\|d_k\|^2&=&\|g_k\|^2-2\xi_1\frac{(g_k^{\top}g_{k-1})^2}{\|g_{k-1}\|^2}+\xi_1^2\frac{(g_k^{\top}g_{k-1})^2}{\|g_{k-1}\|^4}\|g_{k-1}\|^2\\&=&\|g_k\|^2-(2\xi_1- \xi_1^2)\frac{(g_k^{\top}g_{k-1})^2}{\|g_{k-1}\|^2}\\&\leq&\|g_k\|^2.\end{matrix}
(2.3)

又因 - g_k^{\top}d_k\geq (1-\xi_1)\|g_k\|^2, 则(g_k^{\top}d_k)^2\geq(1-\xi_1)^2\|g_k\|^4.此结合 (2.3) 式有

\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}\leq\frac{\|d_k\|^2}{(1-\xi_1)^2\|g_k\|^4}\leq\frac{\|g_k\|^2}{(1-\xi_1)^2\|g_k\|^4}= \frac{1}{(1-\xi_1)^2\|g_k\|^2}.

联立 (i)-(iii), 得

\begin{matrix}\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}&\leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\max \left\{1,\frac{1}{(1-\xi_1)^2}\right\} \frac{1}{\|g_k\|^2}\\&=&\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\frac{1}{(1-\xi_1)^2}\frac{1}{\|g_k\|^2}\\&\leq&\frac{1}{(1-\xi_1)^2}\sum\limits_{i=1}^{k} \frac{1}{\|g_i\|^2}\leq\frac{1}{(1-\xi_1)^2} \cdot \frac{k}{\lambda},\end{matrix}

即 \frac{(g_k^{\top}d_k)^2}{\|d_k\|^2} \geq \frac{(1-\xi_1)^2 \lambda}{k}. 于是\sum\limits_{k=1}^{\infty} \frac{(g_k^{\top}d_k)^2}{\|d_k\|^2}\geq(1-\xi_1)^2\lambda \sum\limits_{k=1}^{\infty} \frac{1}{k}= \infty,与 Zoutendijk 条件矛盾, 从而结论成立.

3 EHS-RD2 方法

引理3.1 EHS-RD2 搜索方向有充分下降性, 即

g_k^{\top} d_k\leq-\min \left\{\frac{\mu_2}{1+\mu_2}, 1-\xi_2 \right\}\|g_k\|^2.

证 数学归纳法. 当 k\in N_{1}, 有

g_1^{\top} d_1=-\|g_1\|^2 \leq -\min \left\{\frac{\mu_2}{1+\mu_2}, 1-\xi_2 \right\}\|g_k\|^2.

当 k \geq 2 时, 设 g_{k-1}^{\top}d_{k-1}<0, 下面分两种情形完成证明.

(i) 若 k\in N_{2}= \{k | k \geq 2, \ g_k^{\top}d_{k-1}\geq0\}, 结合 g_{k-1}^{\top}d_{k-1}<0,有

\begin{matrix}0 \leq \beta_k^{\rm EHS2}& =&\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{(1+\mu_2)g_k^{\top}d_{k-1}-g_{k-1}^{\top}d_{k-1}}\leq\frac{\|g_k\|^2}{(1+\mu_2)g_k^{\top}d_{k-1}-g_{k-1}^{\top}d_{k-1}}\\& <& \frac{\|g_k\|^2}{(1+\mu_2)g_k^{\top}d_{k-1}}.\end{matrix}

进一步, 得

\begin{matrix} g_k^{\top}d_k &=&-\|g_k\|^2+\beta_k^{\rm EHS2}g_k^{\top}d_{k-1} < -\|g_k\|^2+\frac{\|g_k\|^2}{(1+\mu_2)g_k^{\top}d_{k-1}}g_k^{\top}d_{k-1}\\&=&-(1-\frac{1}{1+\mu_2})\|g_k\|^2.\end{matrix}

(ii) 若 k\in N_{3}, 则

g_k^{\top}d_k=-\|g_k\|^2+\xi_2\frac{(g_k^{\top}d_{k-1})^2}{\|d_{k-1}\|^2}\leq-(1-\xi_2)\|g_k\|^2.

从而, 有 g_k^{\top} d_k\leq-\min \left\{\frac{\mu_2}{1+\mu_2}, 1-\xi_2\right\}\|g_k\|^2.证毕.

定理3.1 设假设 (A1)-(A2) 成立, 迭代点 \{x_{k}\} 由 EHS-RD2 方法产生,则

\liminf\limits_{k\rightarrow\infty} \|g_k\|=0.

证 反证法, 设结论不成立, 则存在 \gamma>0 使 \|g_k\|^2\geq\gamma.

(i) 若 k\in N_{1}, 则 d_1=-g_1, 从而 \frac{\|d_1\|^2}{(g_1^{\top}d_1)^2}=\frac{1}{\|g_1\|^2}.

(ii) 若 k\in N_{2}= \{k | k \geq 2, \ g_k^{\top}d_{k-1}\geq0\} 时, d_k+ g_k= \beta_k^{\rm EHS2}d_{k-1}, 两边同时平方并移项, 有

\|d_k\|^2=(\beta_k^{\rm EHS2})^2\|d_{k-1}\|^2-2g_k^{\top}d_k-\|g_k\|^2.

两边再同除以 (g_k^{\top}d_k)^2, 得

\begin{matrix}\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}&=&\frac{(\beta_k^{\rm EHS2})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}-\frac{2}{g_k^{\top}d_k}-\frac{\|g_k\|^2}{(g_k^{\top}d_k)^2}\\&=&\frac{(\beta_k^{\rm EHS2})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}+\frac{1}{\|g_k\|^2}-(\frac{1}{\|g_k\|}+\frac{\|g_k\|}{g_k^{\top}d_k})^2\\&\leq&\frac{(\beta_k^{\rm EHS2})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}+\frac{1}{\|g_k\|^2}.\end{matrix}
(3.1)

另一方面, 利用 g_{k-1}^{\top}d_{k-1}<0, 由(1.4)式第二个不等式知

d_{k-1}^{\top}y_{k-1} = d_{k-1}^{\top}(g_k-g_{k-1})\geq(\sigma-1)g_{k-1}^{\top}d_{k-1}>0,

结合 g_k^{\top}d_{k-1}\geq0, 有

\beta_k^{\rm EHS2} =\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} \geq 0

和

\begin{matrix}g_k^{\top}d_k&=&-\|g_k\|^2+\beta_k^{\rm EHS2}g_k^{\top}d_{k-1}\\&=&-\|g_k\|^2+\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} g_k^{\top}d_{k-1}\\&=&-\|g_k\|^2+\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} (d_{k-1}^{\top}y_{k-1}+\mu_2g_k^{\top}d_{k-1})\\& &+\frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} g_{k-1}^{\top}d_{k-1} - \frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} \mu_2g_k^{\top}d_{k-1}\\& \leq& \frac{\|g_k\|^2-\frac{(g_k^{\top}y_{k-1})^2}{\|y_{k-1}\|^2}}{d_{k-1}^{\top}y_{k-1} +\mu_2g_k^{\top}d_{k-1}} g_{k-1}^{\top}d_{k-1} \\&=& \beta_k^{\rm EHS2}g_{k-1}^{\top}d_{k-1}\end{matrix}

成立, 于是

0\leq\beta_k^{\rm EHS2} \leq \frac{g_k^{\top}d_k}{g_{k-1}^{\top}d_{k-1}}.

进而, 由上式和 (3.1) 式得

\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2} \leq\frac{(\beta_k^{\rm EHS2})^2\|d_{k-1}\|^2}{(g_k^{\top}d_k)^2}+\frac{1}{\|g_k\|^2} \leq\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\frac{1}{\|g_k\|^2}.

(iii) 若 k\in N_{3}, 则 d_k=-g_k+\xi_2\frac{g_k^{\top}d_{k-1}}{\|d_{k-1}\|^2}d_{k-1}, \xi_2 \in [0,1),从而

\begin{matrix}\|d_k\|^2&=&\|g_k\|^2-2\xi_2\frac{(g_k^{\top}d_{k-1})^2}{\|d_{k-1}\|^2}+\xi_2^2\frac{(g_k^{\top}d_{k-1})^2}{\|d_{k-1}\|^4}\|d_{k-1}\|^2\\&=&\|g_k\|^2-(2\xi_2- \xi_2^2)\frac{(g_k^{\top}d_{k-1})^2}{\|d_{k-1}\|^2}\\&\leq&\|g_k\|^2\end{matrix}
(3.2)

又由于 - g_k^{\top}d_k\geq (1-\xi_2)\|g_k\|^2, 进而 (g_k^{\top}d_k)^2\geq(1-\xi_2)^2\|g_k\|^4. 此结合 (3.2) 式有

\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}\leq\frac{\|d_k\|^2}{(1-\xi_2)^2\|g_k\|^4}\leq\frac{\|g_k\|^2}{(1-\xi_2)^2\|g_k\|^4}=\frac{1}{(1-\xi_2)^2\|g_k\|^2}.

联立上述 (i)-(iii) 得

\begin{matrix}\frac{\|d_k\|^2}{(g_k^{\top}d_k)^2}&\leq&\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\max \left\{1,\frac{1}{(1-\xi_2)^2}\right\}\frac{1}{\|g_k\|^2}\\&=&\frac{\|d_{k-1}\|^2}{(g_{k-1}^{\top}d_{k-1})^2}+\frac{1}{(1-\xi_2)^2}\frac{1}{\|g_k\|^2}\\&\leq&\frac{1}{(1-\xi_2)^2}\sum\limits_{i=1}^{k}\frac{1}{\|g_i\|^2}\\&\leq&\frac{1}{(1-\xi_2)^2} \cdot \frac{k}{\gamma}\end{matrix}

于是 \frac{(g_k^{\top}d_k)^2}{\|d_k\|^2} \geq \frac{(1-\xi_2)^2 \gamma}{k}. 从而\sum\limits_{k=1}^{\infty} \frac{(g_k^{\top}d_k)^2}{\|d_k\|^2}\geq(1-\xi_2)^2 \gamma \sum\limits_{k=1}^{\infty} \frac{1}{k}= \infty,与 Zoutendijk 条件矛盾, 因此结论获证.

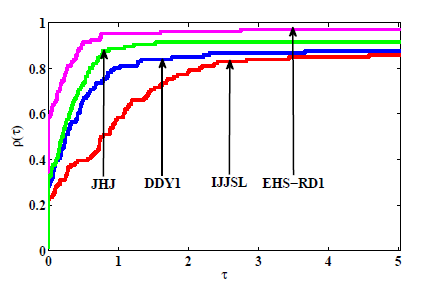
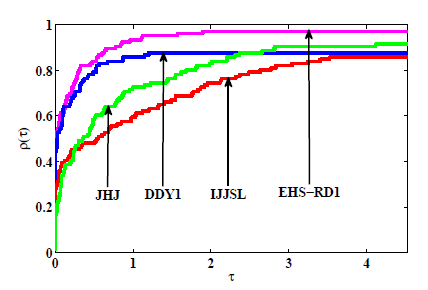
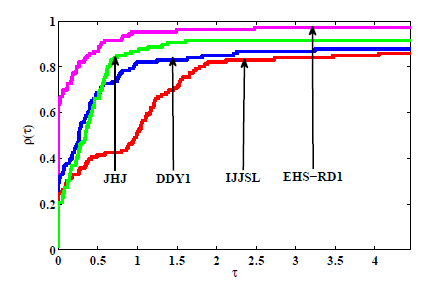
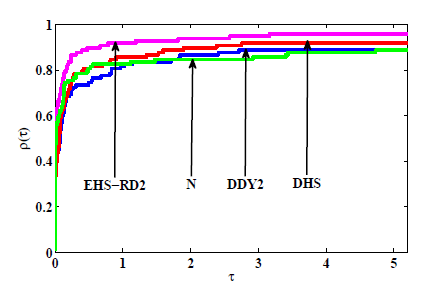
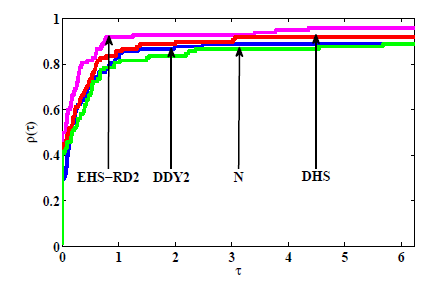
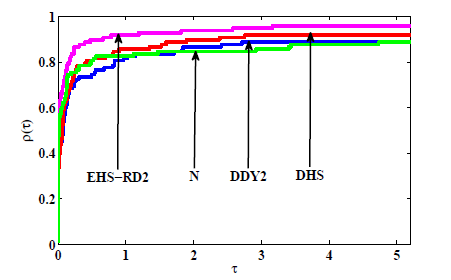
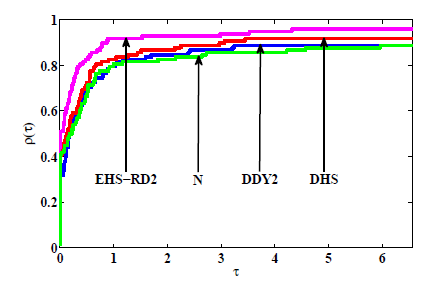
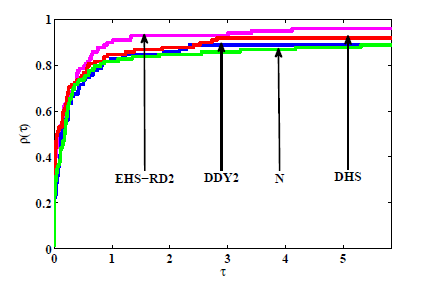
4 数值试验

该节进行两组试验分别验证 EHS-RD1 方法和 EHS-RD2 方法的数值性能. 所有测试均在弱 Wolfe 线搜索 (1.4) 下进行, 其参数选取与文献[9] 保持一致, 即 \delta=0.01, \ \sigma=0.1. 测试环境为 Matlab R2007b, Windows 11 操作系统, Lenovo 笔记本 (AMD Ryzen 5 5600U, Radeon Graphics 2.30 GHz) 16 GB 内存. 出现下面 (i)-(ii) 任一种情形, 方法运行停止. (i) \| g_k\|\leq 10^{-6}; (ii) 迭代次数(Itr)>2000. 当出现 (ii) 时认为该方法对此算例无效, 并记为“F”.

第一组: 将 EHS-RD1 方法与 DDY1 方法[9], IJJSL 方法[10], JHJ 方法[14] 比较测试性能. EHS-RD1 方法中取 \xi_1=0.05, \mu_1=0.04, 其余方法参数选取与原文献一样. 从常用无约束问题集中选取 106 个算例, 其中前 57 个 (从 {\rm bard} 到 woods) 来自 CUTEr 问题集[25], 余下来自文献[26,27]. 算例维数从 2 至 1000000.

第二组: 将 EHS-RD2 方法和 DDY2 方法[9], DHS 方法[12], N 方法[12] 进行数值性能比较. EHS-RD2 方法中取 \xi_2=0.04, \mu_2=10.0, 其余方法参数取值与原文献一致. 98 个算例从常用无约束问题集中选取, 其中算例 1-49 (从 bard 到 watson) 来自 CUTEr 问题集[25], 其余来自文献$[26,27]$. 算例维数从 2 至 1000000.

数值试验结果对迭代次数 (Itr), 函数计算次数 (NF), 梯度计算次数 (NG), CPU 计算时间 (Tcpu) 及方法停止时梯度值 \|g_{*}\| (精度) 这 5 个指标分别进行报告, 为节省篇幅, 具体数值结果的表1-4 见 https://www.cnblogs.com/888-8/p/16334426.html. 此外, 为更直观比较各方法, 采用 Dolan 和 Moré 性能图[28] 刻划测试结果. 图1-4 分别对应第一组迭代次数 (Itr), 函数计算次数 (NF), 梯度计算次数 (NG) 和 CPU 计算时间 (Tcpu) 的比较结果; 图5-8 分别对应第二组迭代次数 (Itr), 函数计算次数 (NF), 梯度计算次数 (NG) 和 CPU 计算时间 (Tcpu) 的比较结果. 性能图具体解释见文献[28], 总体来说, 曲线 \rho(\tau) 越居上方, 其对应方法的数值性能越好. 从图 1-8 看出, EHS-RD1 方法和 EHS-RD2 方法对应的曲线都位于性能图最上方, 其数值性能总体上均优于各组其它比较方法. 这说明, 从给定测试问题集来看, 本文构造的两种新共轭参数与其相应重启方向的结合, 是较为有效的.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   第一组 Itr 性能比较


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   第一组 NF 性能比较


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   第一组 NG 性能比较


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   第一组 Tcpu 性能比较


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   第二组 Itr 性能比较


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   第二组 NF 性能比较


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   第二组 NG 性能比较


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   第二组 Tcpu 性能比较


参考文献

Hestenes M R, Stiefel E.

Methods of conjugate gradients for solving linear systems

Journal of Research of the National Bureau of Standards, 1952, 49(6): 409-436

DOI:10.6028/jres.049.044      URL     [本文引用: 1]

Fletcher R, Reeves C M.

Function minimization by conjugate gradients

Computer Journal, 1964, 7(2): 149-154

[本文引用: 1]

Polak E, Ribière G.

Note sur la convergence de méthodes de directions conjuées

Revue Française Informatique Et De Recherche Opérationnelle, 1969, 3(16): 35-43

[本文引用: 1]

Polyak B T.

The conjugate gradient method in extremal problems. USSR Computational Mathematics and

Mathematical Physics, 1969, 9(4): 94-112

[本文引用: 1]

Dai Y H, Yuan Y X.

A nonlinear conjugate gradient method with a strong global convergence property

SIAM Journal on Optimization, 1999, 10(1): 177-182

DOI:10.1137/S1052623497318992      URL     [本文引用: 1]

Yao S W, Wei Z X, Huang H.

A note about WYL's conjugate gradient method and its application

Applied Mathematics and Computation, 2007, 191(2): 381-388

DOI:10.1016/j.amc.2007.02.094      URL     [本文引用: 3]

Zhang L.

An improved Wei-Yao-Liu nonlinear conjugate gradient method for optimization computation

Applied Mathematics and Computation, 2009, 215(6): 2269-2274

DOI:10.1016/j.amc.2009.08.016      URL     [本文引用: 2]

江羡珍, 马国栋, 简金宝.

Wolfe 线搜索下一个新的全局收敛共轭梯度法

工程数学学报, 2011, 28(6): 779-786

[本文引用: 2]

Jiang X Z, Ma G D, Jian J B.

A new globally convergent conjugate gradient method with Wolfe line search

Chinese Journal of Engineering Mathematics, 2011, 28(6): 779-786

[本文引用: 2]

Zhu Z B, Zhang D D, Wang S.

Two modified DY conjugate gradient methods for unconstrained optimization problems

Applied Mathematics and Computation, 2020, 373( 15): 125004

[本文引用: 5]

Jiang X Z, Jian J B, Song D, Liu P J.

An improved Polak-Ribière-Polyak conjugate gradient method with an efficient restart direction

Computational and Applied Mathematics, 2021, 40(174): 1-24

DOI:10.1007/s40314-020-01383-5      [本文引用: 3]

Kou C X, Dai Y H.

A modified self-scaling memoryless Broyden-Fletcher-Goldfarb-Shanno method for unconstrained optimization

Journal of Optimization Theory and Applications, 2015, 165: 209-224

DOI:10.1007/s10957-014-0528-4      URL     [本文引用: 2]

Jian J B, Han L, Jiang X Z.

A hybrid conjugate gradient method with descent property for unconstrained optimization

Applied Mathematical Modelling, 2015, 39(3/4): 1281-1290

DOI:10.1016/j.apm.2014.08.008      URL     [本文引用: 3]

Dai Z F, Wen F H.

Another improved Wei-Yao-Liu nonlinear conjugate gradient method with sufficient descent property

Applied Mathematics and Computation, 2012, 218(14): 7421-7430

DOI:10.1016/j.amc.2011.12.091      URL     [本文引用: 1]

江羡珍, 韩麟, 简金宝.

Wolfe 线搜索下一个全局收敛的混合共轭梯度法

计算数学, 2012, 34(1): 103-112

DOI:10.12286/jssx.2012.1.103      [本文引用: 2]

对无约束优化问题, 本文给出了一个新的混合共轭梯度法公式. 在标准Wolfe非精确线搜索下,证明了由新公式所产生的算法具有下降性和全局收敛性, 并对算法进行了数值试验, 其结果表明该算法是有效的.

Jiang X Z, Han L, Jian J B.

A new globally convergent mixed conjugate gradient method with Wolfe line search

Mathematica Numerica Sinica, 2012, 34(1): 103-112

DOI:10.12286/jssx.2012.1.103      [本文引用: 2]

对无约束优化问题, 本文给出了一个新的混合共轭梯度法公式. 在标准Wolfe非精确线搜索下,证明了由新公式所产生的算法具有下降性和全局收敛性, 并对算法进行了数值试验, 其结果表明该算法是有效的.

简金宝, 刘鹏杰, 江羡珍.

一个充分下降的谱三项共轭梯度法

应用数学学报, 2020, 43(6): 1000-1012

DOI:10.12387/C2020073      [本文引用: 1]

谱三项共轭梯度法作为共轭梯度法的一种重要推广，在求解大规模无约束优化问题方面具有较好的理论特征与数值效果.本文运用强Wolfe非精确线搜索条件设计产生一个新的谱参数，结合修正Polak-Ribi&#233;re-Polyak共轭参数计算公式建立了一个Polak-Ribi&#233;re-Polyak型谱三项共轭梯度算法.新算法无论采用何种线搜索条件求步长，每步迭代均满足充分下降条件.在常规假设条件下，采用强Wolfe非精确线搜索条件产生步长，证明了算法的强收敛性.最后，对新算法与现有数值效果较好的共轭梯度法进行比对试验，并采用性能图对数值结果进行直观展示，结果表明新算法是有效的.

Jian J B, Liu P J, Jiang X Z.

A spectral three-term conjugate gradient method with sufficient descent property

Acta Mathematicae Applicatae Sinica, 2012, 43(6): 1000-1012

DOI:10.12387/C2020073      [本文引用: 1]

谱三项共轭梯度法作为共轭梯度法的一种重要推广，在求解大规模无约束优化问题方面具有较好的理论特征与数值效果.本文运用强Wolfe非精确线搜索条件设计产生一个新的谱参数，结合修正Polak-Ribi&#233;re-Polyak共轭参数计算公式建立了一个Polak-Ribi&#233;re-Polyak型谱三项共轭梯度算法.新算法无论采用何种线搜索条件求步长，每步迭代均满足充分下降条件.在常规假设条件下，采用强Wolfe非精确线搜索条件产生步长，证明了算法的强收敛性.最后，对新算法与现有数值效果较好的共轭梯度法进行比对试验，并采用性能图对数值结果进行直观展示，结果表明新算法是有效的.

Jiang X Z, Jian J B.

Improved Fletcher-Reeves and Dai-Yuan conjugate gradient methods with the strong Wolfe line search

Journal of Computational and Applied Mathematics, 2019, 348: 525-534

DOI:10.1016/j.cam.2018.09.012      URL     [本文引用: 1]

Liu Y F, Zhu Z B, Zhang B X.

Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing

Journal of Applied Mathematics and Computing, 2022, 68: 1787-1816

DOI:10.1007/s12190-021-01589-8      [本文引用: 1]

Jiang X Z, Liao W, Yin J H, Jian J B.

A new family of hybrid three-term conjugate gradient methods with applications in image restoration

Numerical Algorithms, 2022, 91: 161-191

DOI:10.1007/s11075-022-01258-2      [本文引用: 1]

朱志斌, 耿远航.

一个改进的 WYL 型三项共轭梯度法

数学物理学报, 2021, 41A(6): 1871-1879

[本文引用: 1]

Zhu Z B, Geng Y H.

An modified three-term WYL conjugate gradient method

Acta Mathematica Scientia, 2021, 41A(6): 1871-1879

[本文引用: 1]

马国栋.

强 Wolfe 线搜索下的修正 PRP 和 HS 共轭梯度法

数学物理学报, 2021, 41A(3): 837-847

[本文引用: 1]

Ma G D.

Improved PRP and HS conjugate gradient methods with strong Wolfe line search

Acta Mathematica Scientia, 2021, 41A(3): 837-847

[本文引用: 1]

江羡珍, 廖伟, 简金宝, 毋晓迪.

一个带重启步的改进 PRP 型谱共轭梯度法

数学物理学报, 2022, 42A(1): 216-227

[本文引用: 1]

Jiang X Z, Liao W, Jian J B, Wu X D.

An improved PRP type spectral conjugate gradient method with restart steps

Acta Mathematica Scientia, 2022, 42A(1): 216-227

[本文引用: 1]

袁功林, 吴宇伦, Pham H.

基于非单调线搜索的 HS-DY 形共轭梯度方法及在图像恢复中的应用

数学物理学报, 2022, 42A(2): 605-620

[本文引用: 1]

Yuan G L, Wu Y L, Pham H.

A modified HS-DY-type method with nonmonotone line search for image restoration and unconstrained optimization problems

Acta Mathematica Scientia, 2022, 42A(2): 605-620

[本文引用: 1]

Yuan G L, Zhou Y J, Zhang M X.

A hybrid conjugate gradient algorithm for nonconvex functions and its applications in image restoration problems

Journal of the Operations Research Society of China, 2022, https://doi.org/10.1007/s40305-022-00424-6

URL     [本文引用: 1]

Zoutendijk G. Nonlinear programming computational methods//Abadie J. ed Integer and Nonlinear Programming. Amsterdam: North-Holland, 1970: 37-86

[本文引用: 2]

Gould N I M, Orban D, Toint P L.

CUTEr and SifDec: A constrained and unconstrained testing environment, revisited

ACM Transactions on Mathematical Software, 2003, 29(4): 373-394

DOI:10.1145/962437.962439      URL     [本文引用: 2]

The initial release of CUTE, a widely used testing environment for optimization software, was described by Bongartz, et al. [1995]. A new version, now known as CUTEr, is presented. Features include reorganisation of the environment to allow simultaneous multi-platform installation, new tools for, and interfaces to, optimization packages, and a considerably simplified and entirely automated installation procedure for unix systems. The environment is fully backward compatible with its predecessor, and offers support for Fortran 90/95 and a general C/C++ Application Programming Interface. The SIF decoder, formerly a part of CUTE, has become a separate tool, easily callable by various packages. It features simple extensions to the SIF test problem format and the generation of files suited to automatic differentiation packages.

Moré J J, Garbow B S, Hillstrome K E.

Testing unconstrained optimization software

ACM Transactions on Mathematical Software, 1981, 7: 17-41

DOI:10.1145/355934.355936      URL     [本文引用: 2]

Andrei N.

An unconstrained optimization test functions collection

Advanced Modeling and Optimization, 2008, 10(1): 147-161

[本文引用: 2]

Dolan E D, Moré J J.

Benchmarking optimization software with performance profiles

Mathematical Programming, 2002, 91(2): 201-213

DOI:10.1007/s101070100263      URL     [本文引用: 2]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发