时滞广泛存在于许多实际系统中, 例如通信系统^[1]、 网络控制系统^[2]、电力系统^[3]、多智能体系统^[4]、双边遥系统^[5]等. 时滞的存在使系统的分析与综合变得更加复杂和困难, 同时也导致系统性能变差, 甚至不稳定. 此外, 系统中不确定性的引入, 更准确地描述了模型和实际对象之间的不一致性, 更真实地反映了系统参数变动和干扰的存在. 因此, 研究不确定时滞系统的镇定性问题具有十分重要的理论意义和实际应用价值.

另一方面, 马尔可夫跳跃系统是一类系统模态受到马尔可夫链约束的特殊切换系统, 它可用于描述结构与参数发生突发性改变的各种系统. 众所周知, 马尔可夫过程的驻留时间服从指数分布且模态转移概率是定常的, 然而, 相比于马尔可夫过程, 半马尔可过程其驻留时间并不局限于指数分布, 它可以服从更一般的分布, 例如 Weibull 分布, Gaussian 分布, Laplace 分布等, 且转移概率为时变的, 这使得研究半马尔可夫跳跃系统的镇定性问题更具一般性. 近年来, 具有半马尔可夫跳跃的时变时滞系统受到越来越多研究者的关注^[6⇓⇓-9]. 文献[7]通过状态反馈控制的方法研究了半马尔可夫跳跃时滞系统的有限时间镇定问题. 文献[8]通过柔性终端方法研究了一类具有时变时滞的连续半马尔可夫跳跃系统的随机稳定性和镇定性问题. 文献[9]通过事件触发和量化的方法研究了一类不确定半马尔可夫跳变系统的扩展耗散滤波器设计问题. 尽管如此, 目前针对这类系统还没有得到充分的研究, 特别是用滑模控制的方法研究具有半马尔可夫跳跃的时变时滞系统的镇定性问题的研究还鲜有提及, 这也是本文的第一个研究动机.

从控制策略的角度来看, 滑模控制方法因其对模型不确定性、参数变化、抗干扰、完全自适应、鲁棒性强、降维、易于实现等优点, 引起了国内外控制界的强烈兴趣. 滑模控制方法适用于连续和离散系统、线性和非线性系统以及确定性和不确定性系统. 近年来, 对马尔可夫跳跃系统的滑模控制已经有了许多研究^{[10⇓⇓-13]}. 文献[11]研究了一类具有时变时滞马尔可夫跳跃不确定系统的滑模控制问题, 基于简约型系统的方法, 给出了随机稳定滑模面存在的充分条件. 文献[12]针对具有时变时滞的奇异马尔可夫跳跃系统的滑模控制问题, 基于积分滑模控制的方法, 给出了一组新的充分条件, 既保证了滑模动力学的随机容许性, 又确定了积分型滑模面函数中的所有参数矩阵, 进而构造趋近控制律. 文献[13]研究了含参数不确定和未知非线性函数的马尔可夫跳变系统的鲁棒滑模控制问题. 基于奇异系统方法和线性矩阵不等式, 给出了线性切换面存在和滑模动力学随机稳定性的充分条件. 设计了滑模控制器, 使闭环系统在有限时间内收敛到切换面. 尽管如此, 文献[10⇓⇓-13]均没有考虑具有半马尔可夫跳跃参数的模型. 与文献[11]类似的方法, 文献[14]研究了半马尔可夫跳跃系统的状态估计和滑模控制器设计问题. 文献[15]研究了一类不确定连续半马尔可夫跳跃系统的输出反馈滑模控制器设计问题. 通过线性变换把原系统变为一个奇异系统, 用奇异系统的方法设计一个线性滑模面, 使滑模面上是随机稳定的, 然后设计一个滑模控制器, 使闭环系统状态轨迹在有限时间内到达切换面.

基于上述文献的比较分析可以发现, 一般滑模控制器的设计是基于两种方法, 一种方法是基于简约型系统的方法, 是用非奇异线性变换的方法将原系统转化为简约型系统, 再对简约型系统进行分析, 这种方法相对复杂和困难, 详见文献[11,14];另一种方法是基于积分滑模控制的方法^[12], 即通过构建一个积分型滑模面函数, 根据滑模控制理论, 获得滑模动力学系统, 再对滑模动力学系统进行分析, 设计积分型滑模控制器, 而针对这种方法, 抖振的处理是一个难点, 如果处理不好会造成资源的浪费甚至不稳定. 而相较于这两种普遍的方法, 奇异系统方法^[13,15]则相对简单和易于处理, 而且控制效果良好, 即通过研究原系统的动力学特性, 结合设计的滑模面, 建立描述滑模完整动力学的奇异系统, 再对奇异系统进行分析, 这种方法不像简约型系统方法那样复杂, 而且抖振的处理较于简单, 只需将符号函数的可调参数取小即可, 因此, 用奇异系统方法研究具有半马尔可夫跳跃的不确定连续时变时滞系统的滑模控制器设计问题具有重要的理论和实际意义. 尽管如此, 文献[13,15]的模型均没有考虑时滞因素的影响, 而在考虑时滞因素的情况下, 构造考虑更多时滞信息和奇异系统特性的李雅普诺夫泛函, 以及证明奇异系统是正则且无脉冲的, 进一步得到奇异系统的随机稳定性也是一个难点, 这也是本文的第二个研究动机.

因此本文研究具有半马尔可夫跳跃的不确定连续时变时滞系统的滑模控制器设计问题. 首先, 通过研究原系统的动力学特性, 结合滑模面, 建立描述滑模完整动力学的奇异系统. 然后, 通过构造含有时滞的 Lyapunov 泛函, 建立滑模面存在的充分条件, 保证滑模动力学系统的随机稳定性. 此外, 通过设计滑模控制器, 使闭环系统最终收敛到滑模面. 最后, 通过一个数值算例验证本文方法的有效性.

为了简化表述, 我们有必要做如下的符号说明：$Sym\{A\}$ 表示 $A+A^{T}$;${\rm E\left\{\cdot\right\}}$ 表示数学期望;$\left\|\cdot\right\|$ 是指向量的欧几里得范数或矩阵的欧几里得范数.

给定一个全概率空间 $(\Omega,F,P)$, 考虑如下具有半马尔可夫跳跃的不确定时变时滞系统

其中, $x(t)\in R^{n_{x}}$ 是系统的状态向量；$u(t)\in R^{n_{u}}$ 是控制输入;$\varphi(t)$ 是 $R\longrightarrow R^{n_{x}}$ 上的连续函数;$d(t)$ 表示时变时滞, 满足 $0<d(t)\leq d < \infty$, $\dot{d}(t)\leq\mu$; $\{r(t),t \geq 0\}$ 是具有右连续轨迹的半马尔可夫过程, 并且其在有限集合 $l=\{1,2,\cdots,N\}$ 内取值, 其转移概率与转移速率的关系定义如下

其中$h>0$, ${{\lim\limits_{h \to 0}}(o(h)/h)=0}$, $\lambda_{ij} (h)\geq 0$, $j\neq i$, 表示系统由 ${t}$ 时刻模态 ${i}$ 跳跃到 ${t+h}$ 时刻模态 ${j}$ 的转移速率, 而 $\lambda_{ii} (h)=-\sum\limits_{j=1,j\neq i}^{N} \lambda_{ij} (h)$ 表示系统在 $t+h$ 时刻依然停留在模态 $i$ 的转移速率.

对于每一个$r(t)=i$, $i\in {l}$, 我们有 $A(r(t))=A_{i}$, $A_{d}(r(t))=A_{di}$, $B(r(t))=B_{i}$, $\Delta{A(t,r(t))}=\Delta{A(t,i)}$, $\Delta{A_{d}(t,r(t))}=\Delta{A_{d}(t,i)}$, 其中系统矩阵 $A(r(t))\in{R^{{n_{x}}\times{n_{x}}}}$, $A_{d}(r(t))\in{R^{{n_{x}}\times{n_{x}}}}$, $B(r(t))\in{R^{{n_{x}}\times{n_{u}}}}$, 为已知的实常数矩阵, 且 $0<n_{u}<n_{x}$, $f(t,x(t),r(t))\in{R^{n_{u}}}$ 是外界干扰信号； $\Delta{A(t,i)}$ 和 $\Delta{A_{d}(t,i)}$ 分别表示非匹配参数不确定性, 且满足范数有界, 本文假设这种不确定性满足以下条件

其中,${f_{i}}$ 为已知有界正数, ${U_{i}}$、${W_{i}}$ 和 ${W_{di}}$ 是已知的具有适当维数的实常数矩阵, ${\Delta_{i}(t)}$ 是时变未知矩阵, 满足 ${\Delta_{i}^{T}(t)}{\Delta_{i}(t)}\leq {I}$.

定义 2.1^[16,17] 给定的标量 $d>0$, 对于奇异半马尔可夫跳跃时滞系统

有如下定义

1)对任意的 ${i\in{l}}$, 如果 $(E_{i},A_{i})$ 是正则的和无脉冲的, 时变时滞 ${d(t)}$ 满足 ${0<d(t)\leq{d}<{\infty}}$, 则称系统 (2.5) 是正则的和无脉冲的.

2)对任意的初始条件 ${\varphi(t)\in{R^{n_{x}}}}$ 和 ${r_{0}\in{l}}$, 使得系统 (2.5) 满足

则称系统 (2.5) 是随机稳定的.

引理 2.1^[18] 若对称正定矩阵 ${R>0}$, ${x(t)}$ 是一个可微函数：$[a,b]\longrightarrow{R^{n}}$, 则下列不等式成立

其中 $\Omega={\int_{a}^{b}{x(s){\rm d}s}-{\frac{2}{b-a}}\int_{a}^{b}\int_{\beta}^{b}x(s){\rm d}s{\rm d}\beta}.$

引理 2.2^[19] 若对任意矩阵 $D\in{R}^{n\times{n_{f}}}$, $E\in{R}^{{n_{f}}\times n}$, $F\in{R}^{n_{f}\times{n_{f}}}$, 有 $\left\|{F}\right\|\leq{1}$, 标量 $\varepsilon>0$, 则有下列不等式成立

本文的目的是用奇异系统方法设计一个线性滑模面, 使系统在滑模面上是随机稳定的. 通过设计一个滑模控制器, 使闭环系统的状态轨迹将最终到达滑模面.

对于半马尔可夫跳跃系统 (2.1), 我们设计如下滑模面

其中 $C_{i}\in{R^{{n_{u}}\times{n_{x}}}}$, 对于系统 (2.1), 注意到 $B_{i}\in{R^{{n_{x}}\times{n_{u}}}}$ 为列满秩矩阵, 则总存在一个行满秩矩阵 $Q_{i}\in{R^{{(n_{x}-n_{u})}\times{n_{x}}}}$ 使得 $Q_{i}B_{i}=0$.于是, 我们可以构造一个非奇异矩阵 ${\rm T}_{i}\in{R^{{n_{x}}\times{n_{x}}}}$, 对于任意的 $i\in{l}$ 都有${{\rm T}_{i}}=\left[\begin{array}{ccc} Q_{i}\\ B_{i}^{T} \end{array}\right]$. 因此, ${Q_{i}}{{\rm T}_{i}^{-1}}=\left[\begin{array}{ccc} I\ & 0_{(n_{x}-n_{u})\times{n_{u}}} \end{array}\right]$.

对于系统 (2.1), 等式两边同时左乘 ${{\rm T}_{i}}$ 可得

利用 ${Q_{i}}{B_{i}}=0$, 可以得到

其中${B_{i}^{T}}{B_{i}}$ 是可逆的, 又因为 ${B_{i}}$ 是列满秩的. 根据滑模控制理论^[20], 显然, 系统 (2.11) 的第一个方程表征了系统(2.1) 的部分滑模动力学, 再结合 $s(t,r(t))=0$, 得到了完整的滑模动力学方程, 即

其中

值得注意的是, 将原系统 (2.11) 的第一个方程与滑模面 (2.9) 相结合, 滑模动力学系统可以用系统 (2.12) 来完全描述. 显然, 系统 (2.12) 的随机稳定性保证了指定的滑模面 (2.9) 的存在性. 因此, 我们将提出滑模面 (2.9) 存在的一个充分条件.

定理 3.1 如果存在一组正定对称矩阵 $R_{1},R_{2},R_{3},P_{1i},i\in{l}$ 和任意适当维数矩阵 $N_{1},N_{2}$, 标量 $\varepsilon{_{1}}>0,\varepsilon{_{2}}>0,\varepsilon{_{3}}>0,\varepsilon{_{4}}>0,\varepsilon{_{5}}>0,\varepsilon{_{6}}>0,d>0,0\leq{\mu}<{1}$ 使得 (3.1) 式成立, 则方程(2.12) 是随机稳定的.

其中${C_{i}}={P_{2i}^{-T}}\bar{C_{i}}$, ${P_{2i}}$ 为任意非奇异矩阵.

证 构造如下Lyapunov泛函

其中

并且 ${E^{T}(r(t))}{P(r(t))}={P^{T}(r(t))}{E(r(t))}\geq{0},R_{1}>0,R_{2}>0,R_{3}>0$ 可知 $V(x(t),r(t),t)>0$. 另一方面, 采用文献[15]中相同的弱无穷小算子 $L$, 则 $V(x(t),r(t),t)$ 沿系统 (2.12) 的导数被计算如下

其中 $\bar{\lambda}_{ij}:=E\{\lambda_{ij}(h)\}=\int_{0}^{\infty}{\lambda_{ij}(h)}{g_{i}(h)}{\rm d}h$, ${g_{i}(h)}$ 为逗留时间 $h$ 在模态 $i$ 时的概率密度函数.

根据引理 2.1, 我们有

其中 $\Theta={\int_{t-d}^{t}{x(s){\rm d}s}-{\frac{2}{d}}\int_{t-d}^{t}\int_{\theta}^{t}x(s){\rm d}s{\rm d}\theta}.$

为了使矩阵 $\left[\begin{array}{ccc} \bar{A}_{i}(t) & \bar{A}_{di}(t) \end{array}\right]$ 和 $E_{i}$ 中的块一致, 我们将 $P_{i}$ 划分为

其中$P_{1i}\in{R^{{(n_{x}-n_{u})}\times{(n_{x}-n_{u})}}}$, $P_{2i}\in{R^{{(n_{u})}\times{(n_{u})}}}$, $P_{3i}\in{R^{{(n_{x}-n_{u})}\times{(n_{u})}}}$, $P_{4i}\in{R^{{(n_{u})}\times{(n_{x}-n_{u})}}}$.

然后根据 ${E^{T}(r(t))}{P(r(t))}={P^{T}(r(t))}{E(r(t))}\geq{0}$ 有

根据 ${{\rm T}_{i}}=\left[\begin{array}{ccc} Q_{i}\\ B_{i}^{T} \end{array}\right]$, 可得

因此, 我们可以得到 $P_{1i}\geq{0},P_{3i}={0}$, 且 $P_{4i}$ 可为任意矩阵, 因为 (3.5)-(3.7)式为等价变换, 且 $P_{i}$ 非奇异, 则有 $P_{1i}>{0}$, 因此, 在这种情况下, $P_{i},i\in{l}$ 可以直接表示为

为使滑模面计算过程易于处理且有更低的保守性, 通过观察方程 (2.12) 中系统矩阵的内部结构, 可以发现滑模面参数 $C_{i},i\in{l}$ 在滑模系统矩阵 $\left[\begin{array}{ccc} \bar{A}_{i}(t) & \bar{A}_{di}(t) \end{array}\right]$ 的第一行中不存在, 我们可以进一步将 $P_{i},i\in{l}$ 表示为

其中 $H\in{R^{{(n_{u})}\times{(n_{x}-n_{u})}}}$ 为任意矩阵.

然后把 $P_{i}$代入(3.3) 式中的 $2x^{T}(t){E_{i}^{T}}{P_{i}}\dot{x}(t)$, 又因为 ${E^{T}(r(t))}{P(r(t))}={P^{T}(r(t))}{E(r(t))}\geq{0}$, 我们有

根据系统 (2.12), 对于任意适当维数的矩阵 $N_{1}$ 和$N_{2}$, 有下面的不等式成立

再根据引理 2.2, 对于任意的 $\varepsilon_{1}>0,\varepsilon_{2}>0,\varepsilon_{3}>0,\varepsilon_{4}>0,\varepsilon_{5}>0,\varepsilon_{6}>0$, 有

由 (3.3)-(3.4)式, (3.10)-(3.17)式, 我们有

其中

利用 Schur 补引理和 (3.1) 式可得到 ${\Omega}<0$. 那么对于任意的 $i\in{l}$, 有 $L[V(x(t),r(t),t)]<0$, 因此, 存在一个常数 $c>0$, 使得

根据 Dynkin 公式, 我们得到

当 $t\rightarrow{\infty}$ 时, 可以得到

根据定义 2.1, 可得到系统 (2.12) 是随机稳定的, 即得到定理 3.1, 从而证明结束.

注 3.1 事实上, 使得 $Q_{i}B_{i}=0$ 的 $Q_{i}$ 并不是唯一的, 本文选择 $Q_{i}\in{R^{{(n_{x}-n_{u})}\times{n_{x}}}}$, 是为了构造 ${{\rm T}_{i}}=\left[\begin{array}{ccc} Q_{i}\\ B_{i}^{T} \end{array}\right]$ 为一个非奇异矩阵.

注 3.2 事实上 (2.10)式中变换矩阵 ${{\rm T}_{i}}$ 的构造并不是唯一的. 研究系统(2.12) 中这些变换矩阵的选择对滑模动力学稳定性的影响具有重要的意义.为此, 对于任意满足 ${\cal T}_{i}B_{i}={\left[\begin{array}{ccc} 0_{(n_{x}-n_{u})\times{n_{u}}} & {\cal B}_{i}^{T} \end{array}\right]}^{T}$ 的非奇异矩阵 ${\cal T}_{i}$, 其中 ${\cal B}_{i}\in R^{{n_{u}}\times{n_{u}}}$是非奇异的, 则 ${\cal T}_{i}$ 可以被参数化为

其中 $\phi_{1i}\in{{\cal R}^{(n_{x}-n_{u})\times{(n_{x}-n_{u})}}}$ 和 $\phi_{2i}\in{{\cal R}^{n_{u}\times{n_{u}}}}$ 是任意可逆矩阵, 一般矩阵 $\phi_{3i}\in{{\cal R}^{n_{u}\times{(n_{x}-n_{u})}}}$, 将 ${\cal T}_{i}$ 与系统 (2.1) 左右两边相乘, 并考虑 $s(t,r(t))=0$, 将滑模动力学方程重新表示为

或者, 等价地

其中 ${{\cal Q}_{i}}=\phi_{1i}{Q_{i}}$, 由于 $\phi_{1i}$ 的可逆性, 根据奇异系统理论可知, 系统 (3.24) 的稳定性与系统 (2.12) 的稳定性等价.

注 3.3 值得一提的是, 矩阵 $Q_{i}$ 或 ${\rm T}_{i}$ 的选择对定理 3.1 中结果的可行性没有影响. 具体来说, 根据(3.8)和(3.22)式中的定义, 我们将 Lyapunov 矩阵重新赋值为

由(3.25)式可知, 变换矩阵 ${\cal T}_{i}$ 中的松弛变量 $\phi_{1i}$ 和 $\phi_{2i}$ 可以包含在变量 ${\cal P}_{i}$ 的 $\bar{{\cal P}}_{1i}$ 和 $\bar{{\cal P}}_{2i}$ 中, 其公式与 (3.9) 式类似. 与定理 3.1 的证明类似, 可以立即得出结论, 定理 3.1 中结果的可解性与 ${\cal T}_{i}$ 的选择无关.

注 3.4 值得注意的是, 与正则系统不同, 奇异系统的解可能是不容许的, 即解可能存在脉冲摄动. 因此, 在研究奇异系统的稳定性之前, 需要研究奇异系统的正则性和无脉冲性. 已知 $L[V(x(t),r(t),t)]<0$, 由 (3.3)-(3.4)式, (3.10)-(3.17)式, 可以得到

令 ${N_{1}^{T}}{Q_{i}}A_{i}=G_{i}$, 又因为 ${E_{i}^{T}}{P_{i}}={P_{i}^{T}}{E_{i}}\geq{0}$, 因此, 我们有

然后, 我们证明系统 (2.12) 是正则且无脉冲的. 因为 $rank(E_i)=r<n_{x}$, 因此存在两个非奇异矩阵 $F_i$ 和 $V_i$, 使得

因此, 由 ${E_{i}^{T}}{P_{i}}={P_{i}^{T}}{E_{i}}$ 可知 ${\tilde{P}_{i12}}=0$, 然后, 对 (3.27) 式左乘右乘 ${V_{i}^{T}}$ 和 ${V_{i}}$, 可以得到

这意味着 ${\tilde{\bar{A}}(t)}_{i22}$ 是非奇异的, 因此 $(E_{i},{\bar{A}}_{i}(t))$ 是正则且无脉冲的, 因此根据定义 2.1, 可得到系统 (2.12) 是正则且无脉冲的.

定理 4.1 若考虑系统 (2.1), 滑模面 (2.9), $C_{i}$ 可通过定理 3.1 计算得到, 从而可以设计滑模控制器为

其中

$k_{i}>0,i\in{l}$是一个可调的小参数, 则闭环系统的状态轨迹将最终收敛到滑模面上.

证 由(2.1)(2.9)(4.1)式得到滑模面满足

构造如下 Lyapunov 函数

对于每一个 $i\in{l}$, 沿着 (4.3) 式解的轨迹求弱无穷小算子, 可得

其中$\bar{k}_{i}=\frac{\sqrt{2}}{4}{k}_{i}$, 因此, 根据文献[引理 2] 可知, 由系统 (2.1) 和滑模控制器 (4.1) 组成的闭环系统的状态轨迹将最终到达滑模面, 即得到定理 4.1, 从而证明结束.

考虑具有半马尔可夫跳跃的不确定时变时滞系统, 具体参数如下所示.

模态一

模态二

两种模态的半马尔可夫跳变过程的转移速率矩阵 $\lambda_{ij}(h)$ 被描述为

考虑 Weibull 分布的性质, 我们得出(5.1)式中的转移速率函数对应的逗留时间可以利用 Weibull 分布进行模拟, 且概率密度函数

特别地, 当 $i=1$ 时, 转移速率函数 $2h$ 可以用尺度参数 $\alpha=1$, 形状参数 $\beta=2$ 的 Weibull 分布来表示, 即 $g_{1}(h)=2he^{-h^{2}}$.当 $i=2$ 时, 转移速率函数 $3h^{2}$ 可以用尺度参数 $\alpha=1$, 形状参数 $\beta=3$ 的 Weibull 分布来表示, 即 $g_{2}(h)=3h^{2}e^{-h^{3}}$.因此转移速率 $\lambda_{12}(h)$ 的数学期望就可以表示为

对转移速率矩阵 (5.1) 中的其他元素采用同样的方法, 我们得到转移速率矩阵的数学期望为

取 ${Q_{1}}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0 \end{array}\right]$, ${Q_{2}}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right]$, $H=\left[\begin{array}{ccc} 1 & 0 \end{array}\right]$, $\mu=0.97$, $d=5$.

基于以上数据, 求解 (3.1)式, 我们可以得到

取 $P_{21}=P_{22}=1$, 得到

因此, 可得到滑模面函数为

选取可调参数 $k_{1}=k_{2}=0.04$, 滑模控制器通过 (4.1) 设计为

我们考虑如下外界干扰信号

其中

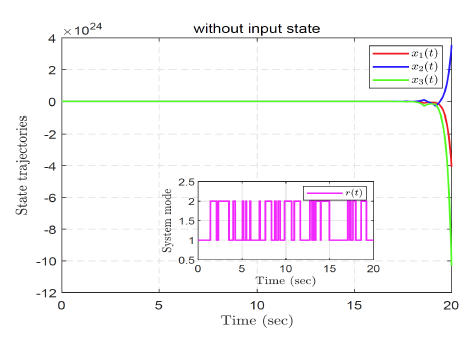
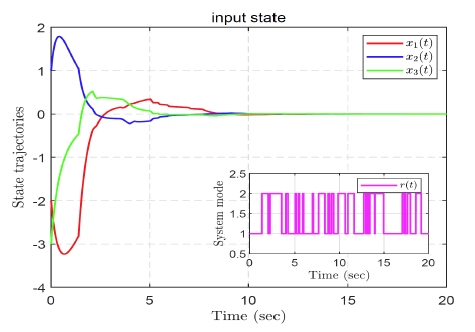
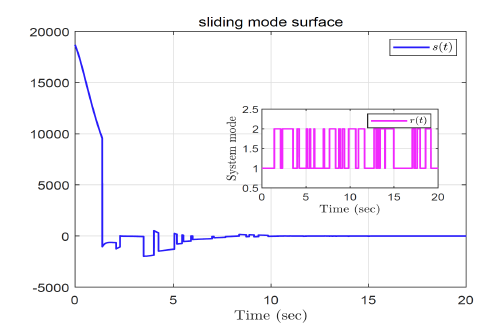
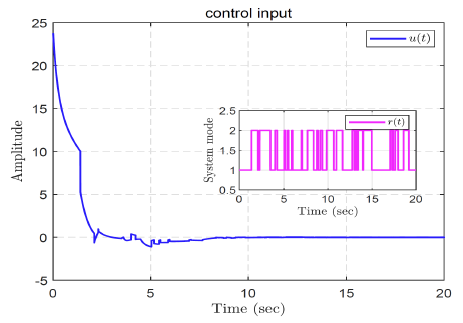
取时滞 $d(t)=4.03+0.97\sin{t}$,初值 $x(0)=\left[\begin{array}{ccc} -2 & 1 & -3 \end{array}\right]$,$\mid{\Delta(t,1)}\mid\leq{1}$,$\mid{\Delta(t,2)}\mid\leq{1}$,利用 Matlab 工具箱对具有半马尔可夫跳跃的不确定连续时变时滞的开环系统和闭环系统的状态轨迹分别进行了仿真.结果如图 1-4所示, 图1和图2分别给出了开环系统和闭环系统的状态轨迹 $x_{1}(t),x_{2}(t),x_{3}(t)$, 即表明了没有控制器作用下的开环系统是不稳定的, 但在本文设计的控制器作用下形成的闭环系统是鲁棒随机稳定的. 图 $3$ 和图 $4$ 分别给出了滑模面函数 $s(t,r(t))$ 和控制输入 $u(t)$ 的轨迹.

针对具有半马尔可夫跳跃的不确定连续时变时滞系统的滑模控制器设计问题, 本文提出了一种新的滑模控制器设计方法.结合原系统的动力学特性和滑模面, 建立了描述滑模完整动力学的奇异系统. 通过构造 Lyapunov 函数, 充分考虑时滞信息, 给出了滑动模态动力学系统的随机稳定分析准则, 并确定了滑模面参数。此外, 设计了滑模控制器, 使闭环系统最终收敛到滑模面. 最后, 通过一个数值算例验证了该方法的有效性.遗憾的是, 该方法没有考虑具有干扰输入 $\nu(t)$ 的情况, 也没有考虑事件触发的滑模控制问题, 这将在未来进一步研究.另一方面, 该方法还可以推广到经典的中立型系统、奇异系统等的滑模控制问题上, 这也将在未来进一步研究.