1 引言
浅水波方程是流体动力学中描述流体运动规律的数学模型, 在海洋、清洁能源、环境与水利工程等众多领域具有广泛应用, 该模型属于非线性双曲守恒律方程, 对应解的结构十分复杂, 很难得到解析解, 因此构造合适的数值格式成为一个研究热点. 目前已有多种数值方法可用来求解浅水波方程, 如TVD(Total Variation Diminishing)格式[1]、WENO(Weighted Essentially Non-oscillatory) 格式[2]、间断有限元(Discontinuous Galerkin)方法[3]以及旋转通量混合格式[4] 等. 一种好的数值格式应具有保平衡性, 即能够准确地保持静水稳态, 如何保持这种微妙的平衡是构造数值格式的一个巨大挑战. 在计算稳态解时通常会出现非物理波, 具有该性质的格式可在一定程度上抑制非物理波的出现.
稳态模拟是浅水波方程中十分重要的研究课题, 很多有趣的现象都会涉及计算静止湖泊的扰动, 不少学者致力于研究具有保平衡性的数值格式, Kurganov等[5]针对具有地形源项的圣维南系统提出了保稳态解的中心迎风格式, 该格式保证了水深的非负性, 可用来计算干旱地区的水流问题. 为了处理复杂计算域的问题, Liu等[6]对二维浅水波方程组构造了一个改进的保平衡中心迎风格式, 格式基于非结构化网格进行离散, 能够精确捕捉干湿界面. 中心迎风格式[7-8]基于黎曼扇进行积分, 不需要特征分解和黎曼求解器, 但是在计算过程中某些变量会出现负值, 与实际意义相违背, 需要对格式进行适当的调整. 除此之外, 早在1987年, Tadmor[9]设计了一种具有二阶精度的熵守恒格式, 并提出一个三点格式如果比熵守恒格式含有更多数值粘性则它是熵稳定的, 根据此性质得到了确定熵稳定格式的方法. 后来, Fjordholm等[10]给出了非平底地形浅水波方程的具有一阶和二阶耗散的保平衡熵稳定格式, 该格式可保持静水稳态和动水平衡态. 为了提高格式的精度, 2018年, 张海军等[11]在数值通量中嵌入限制器, 得到一类高分辨率熵稳定格式, 该格式结合了熵稳定格式和熵守恒格式的优点, 有效抑制了非物理现象的产生.
本文的主要目的是构造求解带源项浅水波方程的高阶保平衡熵稳定格式, 重点在于提出该格式的保平衡性定理并给出相关的理论证明. 首先基于文献[12]中提出的任意高阶熵稳定格式对原耗散项部分进行修正, 变量重构由ENO(Essentially Non-oscillatory) 重构替换为保号WENO-AO(WENO with Adaptive Order)重构[13], 从而得到一类新的高阶熵稳定格式. 为了证明格式的保平衡性, 先介绍了二阶熵守恒格式以及具有一阶耗散的低阶熵稳定格式的保平衡性, 再考虑对源项进行数值离散, 离散方式与所采用的偶数阶熵守恒通量的组合方式相对应, 进而证明高阶熵稳定格式的保平衡性定理, 并通过理论推导、数值实验验证新格式的保平衡性.
2 控制方程
浅水波方程可用来描述溃坝问题、水环境污染问题以及潮汐问题等, 下面给出浅水波方程的具体形式.
2.1 一维浅水波方程
考虑一维具有底部地形源项的浅水波方程
其中, 守恒变量
2.2 二维浅水波方程
二维带源项浅水波方程的表达形式如下
其中守恒变量
3 离散格式
考虑网格均匀划分, 方程(2.1)的半离散有限体积格式为
3.1 熵守恒格式
定义3.1[10] 与
成立, 那么满足该条件的形如(3.1)式的格式称为熵守恒格式, 且具有二阶精度. 类似平底地形浅水波方程的通量构造方式, 得出具有非平底地形源项的浅水波方程的数值通量和源项离散
3.2 熵稳定格式
熵守恒格式在光滑区域计算准确, 但在间断处会有熵耗散, 产生非物理现象, 为了解决该问题, 在熵守恒通量的基础上添加适当的耗散项以获得熵稳定数值通量.
定义3.2[10] 若数值耗散系数矩阵
那么称格式(3.1)为熵稳定格式.熵变量
3.3 高阶熵稳定格式
首先考虑熵守恒通量, 由(3.2)式所计算出的熵守恒通量是二阶精度的, LeFloch等[12]通过对二阶熵守恒通量进行线性组合得到任意偶数阶
其中系数
熵变量采用WENO-AO重构, 具体的构造过程详见文献[13], 记熵变量
定义高阶熵稳定数值通量
注意,
进一步, 高阶熵稳定格式可表示为
其中
4 格式的保平衡性理论
鉴于熵稳定格式本身在求解双曲守恒律问题时已经具备很好的性质, 格式的构造方式是本文的一小部分, 重点在于格式的保平衡性理论. 具有非平坦地形的浅水波方程存在稳态解, 而格式的保平衡性是计算稳态的必要条件, 其关键在于确定合适的离散方式使得非零通量与源项相互抵消, 精确保持该平衡是构造数值格式的一大难点. 当在粗网格中计算方程(2.1)的稳态解时, 稳态的小扰动也会被格式所放大, 所以格式必须满足保平衡性, 才能准确刻画稳态的扰动问题.
稳态解指方程(2.1)与时间变量无关的状态解, 本文主要研究静水稳态, 对一维问题即
如何维持这样的稳态解以及恰当处理带有小扰动的情况是构造数值格式的重点, 格式如果能够保持稳态的离散形式, 则可称为是保平衡的, 有时也表达成“和谐的”。湖泊上的波浪或者深海中的海啸波都是典型的静水扰动问题.
4.1 熵守恒格式的保平衡性
具有(3.3)式熵守恒通量和源项的熵守恒格式(3.1)可整理为
引理4.1[10] 熵守恒格式(4.2)具有保平衡性, 即给定初始数据:
当然, 也可以通过上式说明格式能够保持静水稳态.
4.2 熵稳定格式的保平衡性
熵守恒格式可以保持静水稳态, 能够用来计算稳态的小扰动问题, 但是在激波等间断处会产生伪振荡, 因此, 考虑熵稳定格式的保平衡性.
熵稳定格式的表达形式可整理为
引理4.2[10] 熵稳定格式(4.4)具有保平衡性, 可保持离散的静水稳态(4.3).
引理4.1和引理4.2的具体证明过程在文献[10]中已详细给出, 这里不再赘述.
4.3 高阶熵稳定格式的保平衡性
本节将证明3.3节中构造的高阶熵稳定格式的保平衡性, 证明将分成两部分论述, 首先给出任意偶数阶熵守恒格式的保平衡性定理, 然后再将其推广至熵稳定格式.
4.3.1 任意偶数阶熵守恒格式的保平衡性
定理4.1 在恰当的源项离散形式下, 如果数值通量具有(3.5)式的形式,那么离散格式(3.1)是保平衡的.
证 以四阶熵守衡通量为例来证明熵守恒格式的保平衡性, 为方便起见, 记
其中,
注意, 为了证明保平衡性, 这里需要对源项的离散方式进行修正, 与通量的构造方式相对应,
其中,
具有如上数值通量及源项离散形式(4.5)-(4.6)的有限体积格式为
根据引理4.1, 初始状态
根据恒等式
进一步地, 有
又由于对任意的
4.3.2 高阶熵稳定格式的保平衡性
上节证明了数值通量采用四阶熵守恒通量时熵守恒格式的保平衡性, 用类似的方法可以证明六阶乃至任意偶数阶格式有同样性质, 下面考虑高阶熵稳定格式的保平衡性.
定理4.2 高阶熵稳定格式(3.9)保持离散的静水稳态, 具有保平衡性.
证 初始数据若满足对任意的整数
通过熵变量
5 数值算例
下面用几个典型的一维和二维算例来验证格式的保平衡性. 分别用具有熵通量(3.4)的低阶熵稳定格式以及高阶熵稳定格式(3.9)来求解稳态解的小扰动问题. 低阶熵稳定格式的熵守恒部分为二阶熵守恒通量, 耗散项为一阶, 而高阶熵稳定格式具体为熵守恒部分采用四阶熵守恒通量, 耗散项部分采用五阶的WENO-AO重构, 低阶格式和高阶格式的总体精度理论上应分别为一阶和四阶, 两种格式在下文中分别用ES1以及HES 表示. 时间方向采用四阶强稳定Runge-Kutta法[18], 根据算例进一步验证格式的精度及性能.
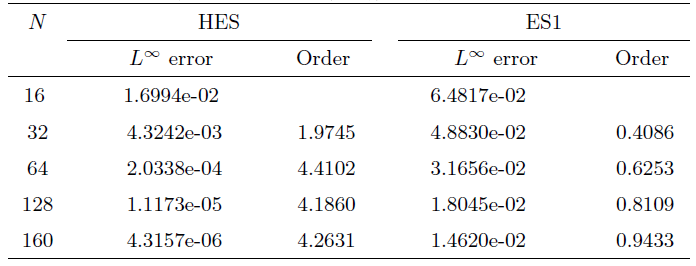
算例1 首先用平底地形(即
不妨取
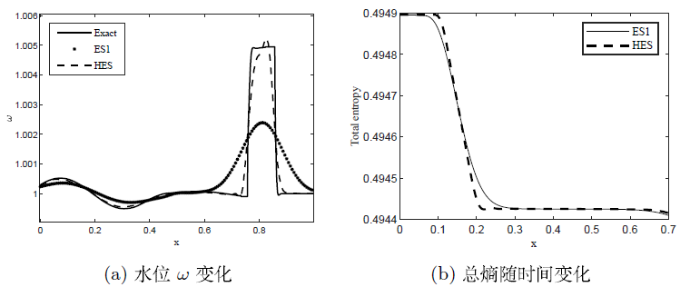
图1
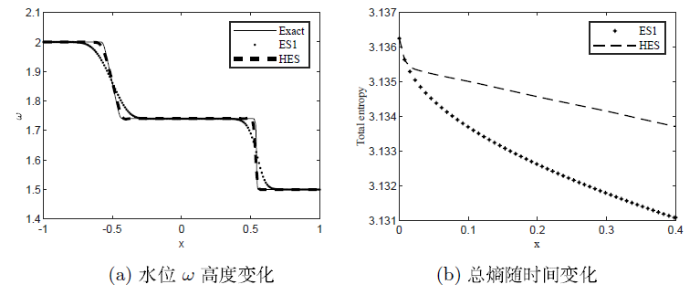
算例2 初始数据是扰动平稳解
这里的
该算例选自文献[5], 重力加速度
假定
图2
图3
图4
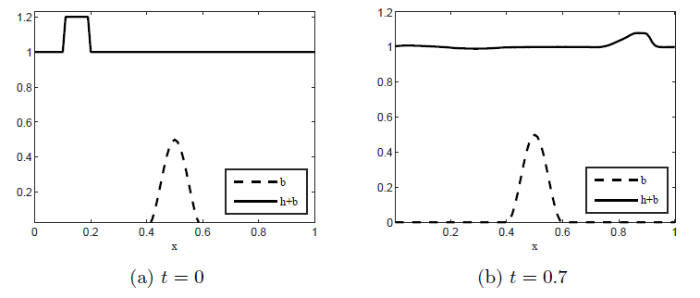
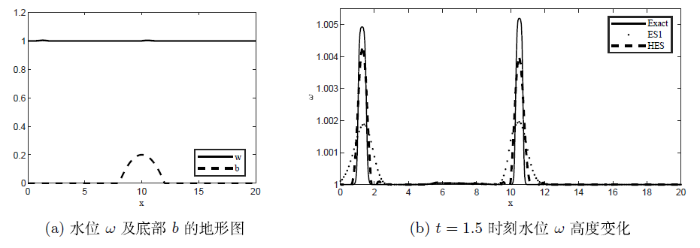
算例3 考虑静止湖泊扰动问题, 湖泊存在一个非常小的扰动, 试图研究这种扰动如何随时间传播, 初始状态为
底部地形是一个抛物形的凸起
采用Neumann边界条件, 重力加速度
图5
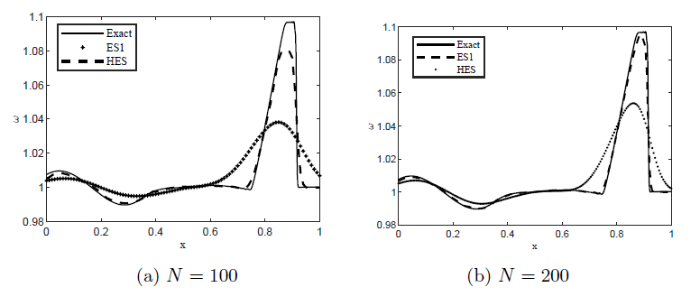
算例4 考虑一维带源项浅水波方程的稳态问题, 底部地形
计算区域
图6
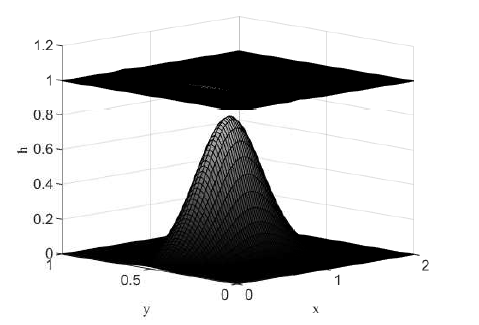
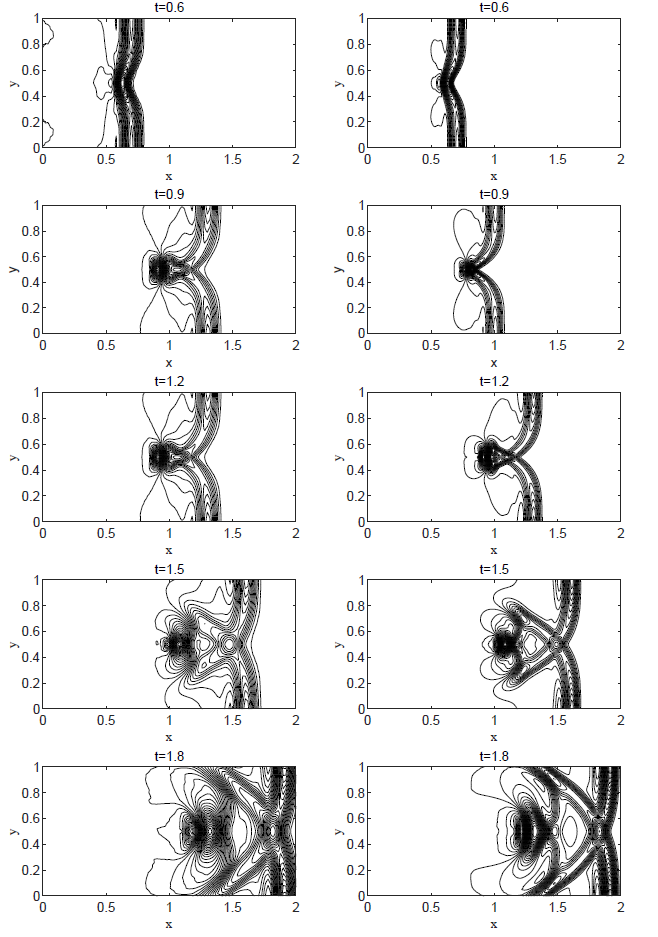
算例5 二维湖泊静止问题, 底部地势是一个椭圆形凸起
其中
图7
图8
6 结论
本文针对具有底部地形源项的浅水波方程设计了一类高阶熵稳定格式, 通过对耗散项部分采用WENO-AO 重构, 确保了格式在实现高精度的同时也满足了保平衡性, 也可以选用其他重构, 例如ENO、WENO重构等. 文中研究的系统主要考虑了底部地形源项, 而底部或者表面的摩擦以及河道宽度的变化等因素还有待进一步研究, 浅水波方程的源项处理方法还有很多进一步研究的内容.
稳态问题是研究浅水波方程的重要课题, 在稳态情况下, 浅水波方程存在非零通量由源项平衡的稳态解, 因此, 所构造的数值格式应该精确捕捉稳态解及其扰动, 文中由保平衡性来刻画这一特点, 证明了高阶熵稳定格式的保平衡性. 稳态包括静水稳态以及动水稳态, 本文主要研究的是静水稳态, 有关动水稳态[20]的性质将在后面继续研究. 最后利用特殊的一维和二维算例进行了数值实验, 旨在说明格式能够很好地处理稳态解的小扰动问题, 但在实际应用中, 常常会面临一些更复杂的情形, 例如, 具有干湿界面的浅水波问题(模拟岛屿周围的水面变化), 以及部分淹没情况下的稳态小扰动问题[6], 对以上特殊情形需要考虑水深
参考文献
Performance of high-resolution TVD schemes for
DOI:10.1080/02533839.2005.9671047 URL [本文引用: 1]
High order finite difference WENO schemes with the exact conservation property for the shallow water matrixs
DOI:10.1016/j.jcp.2005.02.006 URL [本文引用: 1]
A conservative high-order discontinuous Galerkin method for the shallow water matrixs with arbitrary topography
DOI:10.1002/nme.v86.1 URL [本文引用: 1]
求解二维浅水波方程的旋转混合格式
A rotated mixed scheme for solving 2D shallow water matrixs
Central-upwind schemes for the Saint-Venant system
Well-balanced positivity preserving central-upwind scheme with a novel wet/dry reconstruction on triangular grids for the Saint-Venant system
DOI:10.1016/j.jcp.2018.07.038 URL [本文引用: 2]
Semidiscrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi matrixs
DOI:10.1137/S1064827500373413 URL [本文引用: 1]
中心格式在 Saint-Venant 方程组上的应用研究
Research on the application of central scheme in Saint-Venant system
The numerical viscosity of entropy stable schemes for systems of conservation laws
Well-balanced and energy stable schemes for the shallow water matrixs with discontinuous topography
DOI:10.1016/j.jcp.2011.03.042 URL [本文引用: 7]
带源项浅水波方程的高分辨率熵稳定格式
An entropy stable scheme for shallow water matrixs with source terms
Arbitrarily high-order accurate entropy stable essentially non-oscillatory schemes for systems of conservation laws
DOI:10.1137/110836961 URL [本文引用: 3]
保号WENO-AO型中心迎风格式
Sign preserving WENO-AO-type central upwind schemes
Weak solutions of nonlinear hyperbolic matrixs and their numerical computation
DOI:10.1002/(ISSN)1097-0312 URL [本文引用: 1]
A sign preserving WENO reconstruction method
DOI:10.1007/s10915-015-0128-y URL [本文引用: 1]
Essentially non-oscillatory and weighted essentially non-oscillatory schemes
DOI:10.1017/S0962492920000057
URL
[本文引用: 1]

Essentially non-oscillatory (ENO) and weighted ENO (WENO) schemes were designed for solving hyperbolic and convection–diffusion equations with possibly discontinuous solutions or solutions with sharp gradient regions. The main idea of ENO and WENO schemes is actually an approximation procedure, aimed at achieving arbitrarily high-order accuracy in smooth regions and resolving shocks or other discontinuities sharply and in an essentially non-oscillatory fashion. Both finite volume and finite difference schemes have been designed using the ENO or WENO procedure, and these schemes are very popular in applications, most noticeably in computational fluid dynamics but also in other areas of computational physics and engineering. Since the main idea of the ENO and WENO schemes is an approximation procedure not directly related to partial differential equations (PDEs), ENO and WENO schemes also have non-PDE applications. In this paper we will survey the basic ideas behind ENO and WENO schemes, discuss their properties, and present examples of their applications to different types of PDEs as well as to non-PDE problems.
高阶保号熵稳定格式
High order sign preserving stable schemes
求解双曲守恒律方程的任意阶保号熵稳定格式研究
The Research of Arbitrary High-Order Sign Prserving Entropy Stable Schemes for Hyperbolic Conservation Laws
Balancing source terms and flux gradients in high-resolution Godunov methods: the quasi-steady wave-propagation algorithm
DOI:10.1006/jcph.1998.6058 URL [本文引用: 2]