变分不等式问题是求$x^\ast\in C$, 使得

其中$C$是实Hilbert空间$H$中的非空闭凸子集,$\!A: H\to H$是一个单值映射.$\!H$的内积和范数分别为$\langle{\cdot}{\cdot}\rangle$ 与$\|\cdot\|$. 变分不等式问题(1.1)的解集记为$VI(C,A)$.

设映射$T:H\to H$为单值映射. 对于$T$的不动点问题是求$x^\ast\in H$ 满足

设映射$T$的不动点集为Fix$(T)$.

对于变分不等式问题(1.1), 最初的投影算法是由Goldstein^[1] 提出的有限维空间中的梯度投影法

其中$\lambda\in(0,\frac{2\eta}{L^2})$, $L>0$为映射$A$的Lipschitz连续系数, $\eta$为映射$A$的强单调系数, $P_C$是$H$到$C$上的度量投影. 为了证明算法(1.3)的全局收敛性, 文献[1]要求$A$是$\eta$ -强单调, Lipschitz连续的映射. 为了削弱映射$A$的强单调性, Korpelevich^[2]提出外梯度方法

其中$\lambda\in(0,\frac{1}{L})$. 在Hilbert空间中, 若$A$ 是Lipschitz连续的单调映射, 算法(1.4)所产生的序列弱收敛到问题(1.1)的解. 注意到, 算法(1.4)每次迭代需要计算两次非空闭凸集子集$C$上的投影, 当$C$是一个一般可行集时, 投影将难以计算或者计算量很大.

为了避免此缺点, Tseng^[3]给出了解决问题(1.1)的新投影算法. 在迭代的每一步, 该算法只需向可行集$C$ 做一次投影, 算法如下

其中$\lambda\in(0,\frac{1}{L})$. 在算法(1.4)相同假设条件下, 文献[3]中证明了算法(1.5)在Hilbert空间中是弱收敛的.

注意到, 在文献[1⇓-3]中, 为了算法产生的序列收敛, 都需要假设$\lambda\in(0,\frac{1}{L})$, 其中$L$为映射$A$的Lipschitz连续系数. 但是, 映射$A$往往不满足Lipschitz连续条件, 或者即使$A$ 是Lipschitz连续映射, 但往往其Lipschitz连续系数未知. 因此, 很有必要构造新的算法, 削弱该假设条件.

最近, Cai等^[4]给出了空间$H$中求解变分不等式问题(1.1)的惯性Tseng型外梯度算法

其中$r, {l}, \mu$都是常数且满足$r>0$, ${l}\in(0,1), \mu \in(0,1)$, $\lambda_n$取最大数$\lambda\in\{r,r{l},r{l}^2,\cdots \}$ 以满足下列式子成立

序列$\{\alpha_n\}\subset(0,1)$, 序列$\{\beta_n\}\subset(0,1)$ 满足$\lim\limits_{n\to\infty}\beta_n=0$. 在$A$是一致连续伪单调映射, $f$是压缩映射的条件下, 算法(1.6)生成的序列强收敛到问题(1.1)的解.

算法(1.6)的优点在于: 在计算迭代的每一步, 只需向可行集投影一次, 并且不需要假设映射$A$是Lipschitz 连续的, 可获得算法的强收敛性结果.

针对不动点问题(1.2), 许多学者提出了新的迭代方法, 例如: Moudafi^[5]提出的黏性邻近方法, Yamada^[6]提出的混合最速下降法, 更多关于不动点的迭代方法参见文献[7⇓⇓⇓-11].

与此同时, 变分不等式问题与不动点问题公共解的算法研究得到广泛关注. 在2006年, Nadezhkina和Takahashi^[12]基于文献[2], 提出了Hilbert空间中求解问题(1.1)与问题(1.2)公共解的算法

其中$\lambda\in(0,\frac{1}{L}),\{\beta_n\} \subset(0,1)$. 在$A:C\to H$是Lipschitz连续的单调映射, 映射$T:C\to C$是非扩张映射条件下, 文献[12]证明了算法(1.7)的弱收敛性.

为减少向可行集$C$上的投影次数, 削弱映射$T$的非扩张性, Thong和Hieu^[13]

提出在$H$中研究变分不等式问题(1.1)和不动点问题(1.2)公共解的算法

其中$C_n=\{x\in H: \langle{w_n-\lambda_nAw_n-y_n}{x-y_n} \rangle \le0\}$, $\{\beta_n\}\subset(0,1)$满足$\lim\limits_{n\to\infty}\beta_n=0$. $r, {l}, \mu$ 都是常数且满足$r>0$, ${l}, \mu \in(0,1)$, $\lambda_n$取最大数$\lambda\in\{r,r{l},r{l}^2,\cdots \}$以满足下式成立

假设$A:H\to H$是Lipschitz连续的单调映射, $T:H\to H$ 是具有半封闭性的拟非扩张映射. 文献[13]证明了算法(1.8)是弱收敛的.

2021年, Ceng等^[14]为计算空间$H$ 中变分不等式问题(1.1)和不动点问题(1.2)公共解, 提出算法(1.9), 具体形式如下

其中$C_n=\{x\in H: \langle{w_n-\lambda_nAw_n-y_n}{x-y_n}\rangle\le0\}$, $\lambda_n, r, {l}, \mu$取值与文献[13]中取法相同. 序列$\{\alpha_n\}\subset[0,1]$, $\{\beta_n\}, \{\gamma_n\}\subset(0,1)$, 并且对任意$n\ge1$, $\beta_n+\gamma_n<1$, 满足下述条件

(i) $\lim\limits_{n\to \infty}\beta_n=0, \sum\limits^{\infty}_{n=1}\beta_n=\infty$;

(ii) $\sup\limits_{n\ge1}(\alpha_n/\beta_n)<\infty;$

(iii) $ 0<\liminf\limits_{n\to\infty}\gamma_n\le\limsup\limits_{n\to\infty}\gamma_n<1;$

假设$A:H\to H$是Lipschitz连续的伪单调映射, $T:H\to H$ 是非扩张映射, $f$是$\delta$ -压缩映射, $F$是$\kappa$-Lipschitz 连续, $\eta$ -强单调映射. 假设$\Omega$是映射$A$的变分不等式问题和映射$T$的不动点问题的公共解集. 在上述条件成立下, 证明了算法(1.9)生成的序列$\{x_n\}$强收敛到公共解集$\Omega$ 中一点$p$, 并且对任意的$y\in \Omega$, $p$是变分不等式问题$\langle{(\rho F-f)p}{y-p}\rangle\le0$的解.

对于变分不等式和不动点问题公共解的投影算法, 上述文献[12⇓-14]中要求$A$是Lipschitz 连续映射, 文献[12,14]中要求$T$是非扩张映射, 且大多数算法都只具有弱收敛性.

受到文献[4,13-14]的启发, 为求解映射$A$的变分不等式问题(1.1)和映射$T$的不动点问题(1.2)的公共解, 本文提出一个新Tseng型外梯度算法, 该算法的每次迭代只需向可行集进行一次投影. 本文将在$A$是一致连续伪单调映射, $T$是具有半封闭性的拟非扩张映射的假设条件下, 证明算法的强收敛性. 数值实验表明本文算法的有效性.

本节回忆一些基本的定义及引理.

本文总假设$C\subset H$是一个非空闭凸集. 对任意$x\in H$, 在$C$上存在唯一的邻近点, 记为$P_C(x)$, 使得

这里$P_C$叫做$H$到$C$上的投影. 序列$\{x_n\}\subset H$的强收敛与弱收敛分别表示为$x_n\to x$, $x_n\rightharpoonup x$.

定义2.1 称映射$T:C\rightarrow H$是

(i)~ $\eta$ -强单调的, 若存在常数$\eta>0$, 满足 $\langle{ Tx-Ty}{x-y}\rangle\ge\eta\|x-y\|^2,~\forall x,y\in C;$

(ii) 单调的, 若 $\langle{ Tx-Ty}{x-y}\rangle\geq 0,~\forall x,y\in C;$

(iii) 伪单调的, 若 $\langle{Tx}{y-x}\rangle\geq 0\Rightarrow \langle{Ty}{y-x}\rangle\geq 0,~\forall x,y\in C;$

(iv)~ $L$-Lipschitz连续的, 若存在$L>0$, 满足 $\|{Tx-Ty}\| \leq L\|{x-y}\|,~\forall x,y\in C;$

(v) 非扩张的, 若满足 $\|{Tx-Ty}\| \leq \|{x-y}\|,~\forall x,y\in C;$

(vi) 拟非扩张的, 若Fix$(T)\ne \emptyset$, $\|Tx-z\|\le \|x-z\|,~\forall z\in $ Fix$(T), x\in C;$

(vii) 序列弱连续的, 若对于任意的$\{x_n\}\subset C, x_n\rightharpoonup x\Rightarrow Tx_n\rightharpoonup Tx$.

注2.1 由上述定义可知, $\rm{(i)\Rightarrow(ii)\Rightarrow(iii)}$, 反之不成立. 若$\rm{(iv)}$中$L\in(0,1)$, 则称映射$T$是压缩的; 若$L=1$, 则称映射$T$是非扩张的. 非扩张映射一定是拟非扩张映射, 反之不然^[13].

定义2.2^[15] 设映射$T:H\to H$是非扩张映射且Fix$(T)\ne \emptyset$, 称$I-T$在$0$处是半封闭的, 若对于任意的序列$\{x_n\}\subset H$, 满足$x_n\rightharpoonup x$ 和 $(I-T)x_n\to 0$ 时, 有$x\in$ Fix$(T)$ 成立.

注2.2 文献[13]中已经举例说明: 存在映射$T$是拟非扩张的, 但$I-T$在$0$处不是半封闭的.

引理 2.1^[15] 令$C\subseteq H$是一个非空闭凸集. 对于每个$x\in H$, 有下列不等式成立

(i) $\langle{P_{C}(x)-x}{y-P_{C}(x)}\rangle\geq 0,~\forall y\in C$;

(ii) $\|{y-P_{C}(x)}\|^{2} \leq \|{y-x}\|^{2}-\|{P_{C}(x)-x}\|^{2},~\forall y\in C$;

(iii) $\|{\alpha x+(1-\alpha)y}\|^{2}=\alpha \|{x}\|^{2}+(1-\alpha)\|{y}\|^{2}-\alpha(1-\alpha)\|{x-y}\|^{2},~\forall \alpha\in \ Bbb R, y\in H$.

引理 2.2^[16] 设映射$A:H\to H$是伪单调且连续的, 给定点$x^\ast\in C$, 则有

引理 2.3^[17] 设序列$\{a_n\}$是一个非负实序列, 使得

其中$\{\alpha_n\}\subset (0,1)$满足$\sum\limits_{n=0}^\infty \alpha_n=\infty,$$\{b_n\}$ 满足$\limsup\limits_{n\to\infty}b_n \le 0$, 则有$\lim\limits_{n\to\infty}a_n=0$.

引理 2.4^[18] 设$T:C\to H$是非扩张映射, $F:H\to H$ 是$\kappa$-Lipschitz 连续, $\eta$ -强单调映射, 以及常数$\lambda\in(0,1],$$\mu\in(0,\frac{2\eta}{\kappa^2})$. 若映射$T^\lambda:C\to H$ 具有以下形式

则$T^\lambda$是压缩映射, 即对任意$x,y\in C$, 有$\|T^\lambda x-T^\lambda y\| \le (1-\lambda\tau)\|x-y\|,$ 其中 $\tau=1-\sqrt{1-\mu(2\eta-\mu\kappa^2)}\in (0,1].$

引理 2.5^[19] 设序列$\{a_n\}$是一个非负实序列, 存在子列$\{a_{n_i}\}$ 满足$a_{n_i}\le a_{n_i+1},\forall i\in {\Bbb N}$. 则存在一个非减序列$\{m_k\}\subset{\Bbb N},$ 使得$\lim\limits_{k\to\infty}m_k=\infty$, 以及对于充分大的$k\in{\Bbb N},$ 有下述不等式成立

(i) $\|x_{m_k}-p\|^2\le\|x_{m_k+1}-p\|^2$;

(ii) $\|x_{k}-p\|^2\le\|x_{m_k+1}-p\|^2.$

事实上, $m_k$是集合$\{1,2,\cdots, k\}$中满足$a_n\le a_{n+1}$的最大值$n$.

引理 2.6^[20] 设$H_1$和$H_2$是两个实Hilbert空间. 如果映射$A:H_1\to H_2$在$H_1$的有界子集里一致连续, 且$M$ 是$H_1$ 的有界子集, 则$A(M)$ 是有界的.

引理 2.7^[21] 对$x\in H$和$\alpha\ge\beta>0$, 有下述不等式成立

(i) $\frac{\|x-P_C(x-\alpha Ax)\|}{\alpha}\le\frac{\|x-P_C(x-\beta Ax)\|}{\beta};$

(ii) $\|x-P_C(x-\beta Ax)\|\le\|x-P_C(x-\alpha Ax)\|.$

我们假设下述条件成立

条件1 设Fix$(T)\cap VI(C,A)\ne\emptyset.$

条件2 $T$是$H$上的拟非扩张映射, 使得$I-T$在$0$处是半封闭的.

条件3 $A$是$H$上的伪单调映射, 在$H$的有界子集上是一致连续且在$C\subset H$ 上是序列弱连续.

条件4 $f$是$H$上的$\delta$ -压缩映射, $F:H\to H$ 是$\kappa$-Lipschitz连续, $\eta$ -强单调映射, 其中 $\delta<\tau:=1-\sqrt{1-\rho(2\eta-\rho\kappa^2)},\quad \rho\in(0,\frac{2\eta}{\kappa^2})\ \mbox{为常数}.$

条件5 选取实数序列$\{\tau_n\}, \{\beta_n\}, \{\gamma_n\}\subset(0,1)$, $\beta_n+\gamma_n\le 1$, 满足下述条件

(i) $\lim\limits_{n\to\infty}\beta_n=0$, $\sum\limits_{n=1}^\infty \beta_n=\infty;$

(ii) $\lim\limits_{n\to\infty}\tau_n/\beta_n=0;$

(iii) $0<\liminf\limits_{n\to\infty}\gamma_n \le \limsup\limits_{n\to\infty}\gamma_n<1.$

下面, 我们给出本文求问题(1.1)和(1.2)公共解的算法.

我们先证明一些引理.

引理 3.1 本文算法的线搜索程序(3.1)是良定的.

证 若$w_n\in VI(C,A)$, 则有$w_n=P_C(w_n-rAw_n)$. 当$m=0$时,(3.1)式成立.

若$w_n\notin VI(C,A)$, 假设对于任意的$m\ge0$满足下式

即

考虑$w_n$的两种情况. 一方面, 若$w_n\in C$, 因为$A$和$P_C$是连续的, 所以有

由于映射$A$在$H$的有界子集上是一致连续的, 则有

结合(3.4)式, 有

设$t_m:=P_C(w_n-r{l}^mAw_n)$, 结合引理2.1知

等价于

(3.6)式取极限$m\to\infty$, 有

说明$w_n\in VI(C,A),$ 产生矛盾!

另一方面, 若$w_n\notin C$, 有

以及

结合$\mu\in(0,1)$和式子(3.3)知, 产生矛盾! 故算法中线搜索是良定的. 证毕.

引理 3.2 假设条件1-5成立, 算法生成的序列$\{w_n\},\{x_n\},\{y_n\},\{z_n\}$是有界的. 若$x_n-x_{n+1}\to 0, x_n-y_n\to0, x_n-z_n\to0$和$x_n-w_n\to0$, 存在$\{x_n\}$的子序列$\{x_{n_k}\}$弱收敛到$z\in H$, 则有$z\in $ Fix$(T)\cap VI(C,A)$.

证 由(3.2)式可得

等价于

因为$x_n-x_{n+1}\to 0, x_n-z_n\to0, \beta_n\to0, \liminf\limits_{n\to\infty}(1-\gamma_n)>0$ 和序列$\{x_n\},\{z_n\}$是有界的, 可得

已知$x_{n}-y_{n}\to0$和$x_{n}-w_{n}\to0$, 又因为

所以(3.8)式取极限$n\to\infty$, 有$\lim\limits_{n\to\infty}\|w_{n}-y_{n}\|=0$.

由于$x_{n_k}\rightharpoonup z$和$\lim\limits_{k\to\infty}\|x_{n_k}-y_{n_k}\|=0$, 得$y_{n_k}\rightharpoonup z$. 又因为$\{y_n\}\subset C$, 所以$z\in C.$ 由于$y_{n_k}=P_C(w_{n_k}-\lambda_{n_k}Aw_{n_k})$, 根据引理2.1知

等价于

下证: $\liminf\limits_{k\to\infty}\langle{Aw_{n_k}}{x-w_{n_k}}\rangle\ge0.$ 一方面, 考虑$\liminf\limits_{k\to\infty}\lambda_{n_k}>0$ 的情况. 因为$\{w_{n_k}\}$ 是有界的, 并且$A$在$H$的有界子集上是一致连续的. 由引理2.6知, $\{Aw_{n_k}\}$是有界的. 将(3.9)式取极限$k\to\infty$, 有

另一方面, 考虑$\liminf\limits_{k\to\infty}\lambda_{n_k}=0$ 的情况. 由于$x_{n_k}\rightharpoonup z$ 和$x_{n}-w_{n}\to0$, 得$w_{n_k}\rightharpoonup z$. 令$t_{n_k}:=P_C(w_{n_k}-\lambda_{n_k}{l}^{-1}Aw_{n_k})$, 由算法知$\lambda_{n_k}{l}^{-1}>\lambda_{n_k}$, 结合引理2.7得

因此$t_{n_k}\rightharpoonup z\in C$, 即$\{t_{n_k}\}$是有界的. 又因为, $A$在$H$的有界子集上是一致连续的, 所以有

因为$\lambda_{n_k}{l}^{-1}=r{l}^{m_{n_k}-1}$, 由算法的线搜索程序知

等价于

结合(3.11)和(3.12)式知

根据引理2.1知, $t_{n_k}=P_C(w_{n_k}-\lambda_{n_k}{l}^{-1}Aw_{n_k})$具有下述性质

等价于

因为$\{Aw_{n_k}\}$和$\{t_{n_k}\}$皆是有界的, 并且$\|w_{n_k}-t_{n_k}\|\to0$, 结合(3.13)式, 将(3.14)式取极限$k\to\infty$, 有

由$A$在$H$的有界子集上是一致连续的, 并且$\lim\limits_{k\to\infty}\|w_{n_k}-y_{n_k}\|=0$, 可得

因为

结合(3.15)和(3.16)式, 有

任取单调递减正实数列$\{\xi_k\}\subset (0,1).$ 当$k\to\infty$ 时, 有 $\xi_k\to0.$ 对任意的$k\ge1$, 设$l_k$是最小正整数, 使得

由$\{y_{l_k}\}$的定义知$\{y_{l_k}\}\subset C$, 对任意的$k\ge 1$, 有$Ay_{l_k}\ne 0$. 设$h_{l_k}=\frac{Ay_{l_k}}{\|Ay_{l_k}\|^2}$, 因此对任意的$k\ge1$, 有$\langle{Ay_{l_k}}{h_{l_k}}\rangle=1$, 那么(3.17)式可写为

又因为映射$A$是伪单调的, 则有

等价于

下证: $\lim\limits_{k\to\infty}\xi_{k}h_{l_k}=0$. 由于$y_{n_k}\rightharpoonup z$ 且映射$A$在$C$上是序列弱连续的, 则有$Ay_{n_k}\rightharpoonup Az\ne 0$ (否则, $z$是解). 由序列的弱下半连续性, 可得

因为$\{y_{l_k}\}\subset\{y_{n_k}\}$和$\lim\limits_{k\to\infty}\xi_k\to0$, 得

由于$\lim\limits_{k\to\infty}\xi_{k}h_{l_k}=0$, $\{x_{l_k}\}$和$\{y_{l_k}\}$是有界的, 并且$A$是一致连续映射,(3.18)式取极限$k\to \infty$, 对任意$x\in C$, 得 $\liminf\limits_{k\to\infty}\langle{Ax}{x-y_{l_k}}\rangle\ge0$, 即

由引理2.2知, $z\in VI(C,A)$. 又因为$x_n-z_n\to 0$和$x_{n_k}\rightharpoonup z,$ 则有$z_{n_k}\rightharpoonup z$. 结合(3.7)式, 得$Tz_{n_k}-z_{n_k}\to 0$. 由定义2.2知$z\in $ Fix$(T).$ 因此, $z\in$ Fix$(T)\cap VI(C,A)$.证毕.

引理 3.3 设序列$\{w_n\}, \{y_n\}, \{z_n\}$是算法生成的, 则有

证 由于$z_n=y_n-\lambda_n(Ay_n-Aw_n)$, 所以对任意的$p\in {\rm Fix}(T)\cap VI(C,A)$, 有

一方面, 因为$p\in {\rm Fix}(T)\cap VI(C,A)$, 所以对任意的$y_n\in C$, 有$\langle{Ap}{y_n-p}\rangle\ge 0.$ 由于$A$的伪单调性, 对任意的$y_n\in C$, 有$\langle{Ay_n}{y_n-p}\rangle\ge 0.$ 另一方面, 根据$y_n$的定义, 结合引理2.1知, $\langle{y_n-w_n+\lambda_n Aw_n}{y_n-p}\rangle\le 0.$ 代入(3.20)式有

证毕.

定理 3.1 假设条件1-5成立, 算法生成的序列为$\{x_n\}$, 则有$x_n\to p\in {\rm Fix}(T)\cap VI(C,A)$$\Longleftrightarrow x_n-x_{n+1}\to 0$, 其中$p=P_{{\rm Fix}(T)\cap VI(C,A)}(f+I-\rho F)(p)$ 是下述变分不等式的唯一解

证 首先, 证明$P_{{\rm Fix}(T)\cap VI(C,A)}(f+I-\rho F)$是一个压缩映射. 由引理2.4知

根据Banach压缩原则知, $P_{{\rm Fix}(T)\cap VI(C,A)}(f+I-\rho F)$有唯一的不动点, 说明$p\in H$, 即$p=P_{{\rm Fix}(T)\cap VI(C,A)}(f+I-\rho F)(p)$. 因此, 变分不等式(3.21)存在唯一解$p\in {\rm Fix}(T)\cap VI(C,A)$. 为了证明$\lim\limits_{n\to\infty}\|x_n-p\|=0$, 假设$\lim\limits_{n\to\infty}\|x_n-x_{n+1}\|=0$, 具体分为以下四个步骤.

步骤1 证明序列$\{x_n\}$是有界的. 结合引理3.3和$\mu\in(0,1)$, 得$\|z_n-p\|\le\|w_n-p\|$. 由$w_n$的定义知

由$\bar{\alpha}_n$定义和$0\le\alpha_n\le\bar{\alpha}_n$ 知, 对任意的$n\ge1$, 有$\alpha_n\|x_n-x_{n-1}\|\le\tau_n.$ 因为$\lim\limits_{n\to\infty}\frac{\tau_n}{\beta_n}=0$, $\beta_n>0$, 所以有

即$\lim\limits_{n\to\infty}\frac{\alpha_n}{\beta_n}\|x_n-x_{n-1}\|=0$, 说明存在$M_1>0,$ 使得

结合(3.23)和(3.25)式有

又因为$\beta_n+\gamma_n\le1$, 所以有

第一个不等号是由于三角不等式与范数的凸性; 第二个不等号是由于映射$f$是$\delta$ -压缩的和引理2.4; 第三个不等号是由于$1-\beta_n\tau\le1$; 最后一个不等号是由于最大值函数的性质.

由数学归纳法得

因此, 序列$\{x_n\}$是有界的. 同时, 可得$\{w_n\},\{z_n\},\{y_n\},\{f(x_n)\},\{Tz_n\},\{FTz_n\}$皆是有界的.

步骤2 证明$(1-\beta_n\tau-\gamma_n)(1-\mu^2)\|w_n-y_n\|^2\le\|x_n-p\|^2-\|x_{n+1}-p\|^2+\beta_n M_4$.

由$x_{n+1}$的定义知

其中, $M_2=\sup\{2\|(f-\rho F)p\|\|x_{n+1}-p\|\}.$ 第一个不等号是由于范数的性质; 第二个不等号是由于$f$ 是$\delta$ -压缩映射和引理2.4; 第三个不等号是由于二次函数的凸性与Cauchy-Schwarz 不等式.

将(3.26)式左右两边平方有

其中, $M_3=\sup\limits_{n\ge1}\{2M_1\|x_n-p\|+\beta_nM_1^2\}.$ 结合(3.19)式则有

将(3.29)式代入(3.28)式, 得

其中, $M_4=(1-\beta_n\tau-\gamma_n)M_3+M_2$, 那么

等价于

步骤3 证明

由$w_n$的定义知

其中, $M_5=\sup\limits_{n\ge1}\{2\|w_n-p\|\}$, 则有

将(3.32)式代入(3.28)式的倒数第二个不等式, 得

步骤4 假设$\lim\limits_{n\to\infty}\|x_n-x_{n+1}\|=0$, 下证$\lim\limits_{n\to\infty}\|x_n-p\|=0$. 考虑2种情况.

情况1 存在$N\in {\Bbb N}$, 对任意$n\ge N$, 满足$\|x_{n+1}-p\|^2\le\|x_n-p\|^2.$ 当$n\to\infty$时, $\|x_n-p\|^2$ 的极限存在. 由(3.30)式和$\lim\limits_{n\to\infty}\beta_n=0$ 得, $\lim\limits_{n\to\infty}\|w_n-y_n\|=0$. 同时, 由$w_n$ 的定义知

与此同时, 由$z_n$定义与映射$A$ 的一致连续性得

那么有

因为$\{x_n\}$是有界序列, 所以存在子序列$\{x_{n_k}\}$ 弱收敛到$z\in H$, 则有

由于$\|x_n-x_{n+1}\|\to0$, 结合(3.33)式有

结合(3.24)和(3.34)式有

又因为$\{\beta_n(\tau-\delta)\}\subset(0,1]$, $ \sum\limits_{n=1}^\infty\beta_n(\tau-\delta)=0$ 以及(3.35)式成立, 对于(3.31)式, 由引理2.3知, 当$n\to\infty$ 时, 有$x_n\to p$.

情况2 $\{\|x_n-p\|^2\}$存在子列$\{\|x_{n_j}-p\|^2\}$, 对任意$j\in {\Bbb N}$, 有

应用引理2.5, 存在非减序列$\{m_k\}\in {\Bbb N}$, 使得$\lim\limits_{k\to\infty}m_k=\infty,$ 则有

结合(3.30)和(3.37)式有

由于$\lim\limits_{k\to\infty}\beta_{m_k}=0$, 说明$\|w_{m_k}-y_{m_k}\|\to0$. 同情况一可得$x_{m_k}-w_{m_k}\to0,$$ x_{m_k}-z_{m_k}\to0,$$ x_{m_k}-y_{m_k}\to0,$ 并且有下述式子成立

结合(3.31)和(3.36)式得

因为$\beta_{m_k}(\tau-\delta)>0$, 所以有

又由于式子(3.37)知,

结合(3.38)和(3.39)式和(3.40)式知$\limsup\limits_{k\to\infty}\|x_{k}-p\|^2=0,$

即当$k\to\infty$时, 有$x_k\to p$.证毕.

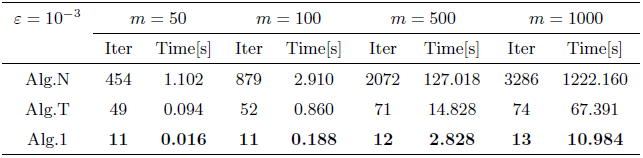
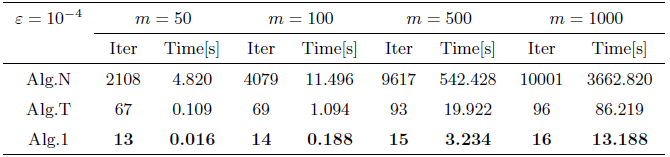
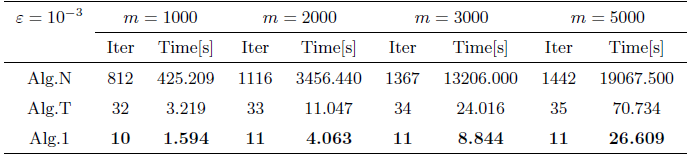
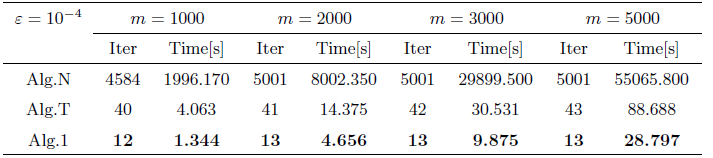
本节计算机检验结果都是用MATLB在CPU型号为Intel(R) Core(TM) 2i5-1035G1 (6核, 主频2.1GHz)和内存为16GB的笔记本电脑上运行的. 将文献[12,定理3.2]中的算法 (记为Alg.N), 文献[算法2] (记为Alg.T) 和本文中算法1 (记为Alg.1)进行比较. 选取$\|x_n-x_{n-1}\|\le\varepsilon$ 作为算法的停止标准, 用Time (单位:秒)记运行所花费的时间, 用Iter记迭代的步数, 我们取例1的最大迭代步数为10000, 取例2的最大迭代步数为5000. 以$x_0=x_1=(1,1,\cdots, 1)$ 为初始点. 三种算法的参数选取如下.

1. Alg.1的参数选取: $r=0.99; l=0.05; \alpha=\mu=0.5; \rho=2; \tau_n=\frac{1}{n^2}; \beta_n=\frac{1}{2(n+1)}; \gamma_n=\frac{n}{2(n+1)}$. 其中, $T(x)=f(x)=F(x)=\frac{x}{3}$.

2. Alg.N的参数选取: $\lambda=0.5; \beta_n=\frac{1}{2(n+1)}$. 并且选取$T(x)=\frac{x}{3}$.

3. Alg.T的参数选取: $r=0.99; l=0.05; \mu=0.5; \alpha_n=\frac{n}{2(n+1)}; \beta_n=\frac{1}{2(n+1)}$. 并且选取$T(x)=\frac{x}{3}$.

例1 考虑文献[22]非线性补问题的算法检验. $Ax=Mx+q,$ 且$M=N^TN+S+D$, 其中$N$是由区间$(-5, 5)$随机生成的$m\times m$维方阵, $S$是由区间$(-5, 5) $ 随机生成的$m\times m$维反对称方阵, $D$是由$(0, 0.3)$ 随机生成的$m\times m$维对角阵, 向量$q$是由区间$(-500, 0)$均匀生成的, 其中可行集 $C=\{x=(x_1,\cdots, x_m)\in \Bbb R^m:x_i\le -1, i=1,\cdots, m\}.$

例2 考虑文献[23]非线性补问题的算法检验, 定义$C=\Bbb R^n_+$, $F(x)=F_1(x)+F_2(x),$ 其中

矩阵$M$是一个$m\times m$的方阵如下, $q=(-1,-1,\cdots, -1)$,

注4.1 相比于文献[4]中算法仅求解变分不等式问题(1.1), 本文中的算法拓展到求解变分不等式问题(1.1)与不动点问题(1.2)的公共解问题; 相较于文献[12]中算法计算一次迭代需要向可行集投影两次, 本文算法每次迭代只需向可行集做一次投影; 对比于文献[12,13]中算法是弱收敛的, 本文算法生成的序列是强收敛的; 相较于文献[14]中算法, 本文映射$T$削弱为具有半封闭性的拟非扩张映射.

注4.2 将文献[12]中的算法 Alg.N, 文献[13]中的算法 Alg.T和本文中算法Alg.1, 对本文中例1和例2的非线性补问题分别进行数值试验, 可发现: 随着问题维数的增大, 精度的减小, 本文的算法 Alg.1所需迭代次数与运行时间都要少于另外两者.