本文研究定常非齐次不可压 Euler 流通过三维柱对称无穷管道的解的适定性和无穷远渐近速率, 管道中可包含障碍物. 三维定常非齐次不可压 Euler 方程为

其中$\rho$, $(u_{1}, u_{2},u_{3})$ 和 $p$ 分别表示密度, 速度和压力.

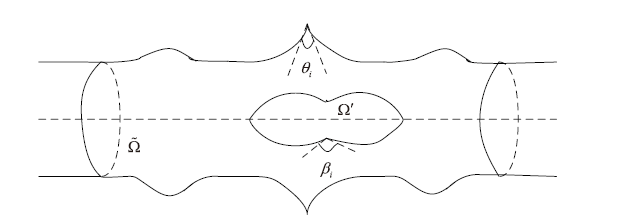
如图1所示, 流体区域是一个内部包含障碍物 $\Omega'$ 的无穷管道区域 $\widetilde \Omega$.

和

其中 $L_{1}$ 和 $L_{2}$ 为常数. 令

函数 $f_1(x_1)$ 和 $f_2(x_1)$ 满足

以及

这里$\Pi=\{P_{ i}\}_{i=1}^m$ 是边界上所有角点的集合, 其中 $\theta_i$ 和 $\beta_i$ 都是严格小于 $\pi$. 记 $\Omega=\tilde\Omega\setminus\Omega'$. 流体在边界满足条件

其中 $\overrightarrow{n}$ 是 $\partial \Omega\backslash\Pi$ 上的单位外法向量. 在本文中的结论都包含 $f_0\equiv0$, 即没有障碍物的情况.

定常不可压 Euler 方程是椭圆-双曲特征耦合的系统, 已有一系列的研究工作. 当密度 $\rho$ 为常数时,方程(1.1)为齐次定常 Euler 方程. 对于齐次定常 Euler 方程的研究主要有两种方法: 涡方法和流函数方法. 涡方法是通过涡/旋函数研究速度场的存在唯一性和相关性质. 利用涡方法研究二维齐次不可压定常 Euler 方程的结果, 可参见文献[1⇓⇓⇓-5]. 流函数方法是由不可压方程引入的流函数, 将齐次定常 Euler 方程转化为关于流函数的椭圆方程. 对于二维的情况, 流函数 $\psi$ 满足椭圆方程

这里的非线性项 $f$ 是 $\psi$ 的函数, 表示流场的旋度, 相关结果见文献[6⇓⇓⇓⇓-11]. 对于三维柱对称非齐次 Euler方程, 经过柱坐标变换可知其旋度由 $\partial_{r}U-\partial_{x}V$ 和 $W$ 两个量表示, 而二维的旋度由单量表示, 因此在旋度方面, 三维柱对称和二维有本质的区别. 对于三维柱对称非齐次的 Euler 方程, 流函数 $\psi$ 满足椭圆方程的非线性项 $f=f\left(\nabla \psi, \psi, r\right)$ 比二维齐次 Euler 方程的非线性项 $f=f\left(\psi\right)$ 更加复杂, 具体推导请见第 2 节. 因此, 三维柱对称非齐次 Euler 方程不能简单的套用二维的方法.

本文研究的是由 Bers^[12]提出的管道问题. 此类问题对应于物理中的风洞实验、实际工程中的油气传输管道等实际场景. 对于可压缩无旋流的研究已经有了大量结果, 可参见文献[13⇓-15]. 相比于无旋流的情况, 有旋流的研究更加复杂. 当旋度满足小性条件时, Xie 和 Xin^[16]证明了二维有旋可压 Euler 流亚音速解的适定性. 对于大旋度情况, Du, Xie 和 Xin^[17]在水平速度的凸性条件下, 证明了二维有旋可压 Euler 流亚音速解的适定性. Chen, Huang, Wang 和 Xiang^[18]去除凸性条件和小性要求, 证明了二维有旋可压 Euler 流亚音速解的适定性. 对于三维柱对称流, Du 和 Duan^[19] 在凸性条件下, 证明了等熵可压 Euler 流亚音速解的适定性, 其后 Du 和 Luo ^[20-21]在凸性假设下, 证明了非等熵可压 Euler 流亚音速解的适定性. 当漩涡速度 $W$ 不等于 0 时, Duan 和 Weng^[22]证明了三维柱对称可压 Euler 流具有小漩涡的亚音速解的适定性. Deng, Wang 和 Xiang^[23]证明了三维柱对称可压 Euler 流具有大漩涡解的适定性. 通过补偿紧性框架, 由绝热指数极限, 即当绝热指数趋向于无穷大时, 定常可压缩 Euler 流体收敛到定常不可压缩 Euler 流体, Chen, Huang, Wang 和 Xiang^[18]和 Deng, Wang 和 Xiang^[23] 分别得到二维和三维柱对称不可压缩 Euler 方程极限解的存在唯一性.

定常 Euler 流研究中的另一个重要问题是研究流体流经障碍物的问题. 无旋流的情况, Shiffman 和 Bers^[24⇓-26]证明二维可压 Euler 流亚音速解的适定性. 对于三维(或更高维)的情况, Finn 和 Gilabarg^[27]证明了当流速低于某一速度时, 三维无旋 Euler 流亚音速解的适定性和渐近性行为. 董光昌^[28]将 Finn 等人的结果扩展到空间维数大于等于三的一般情况. 对于有旋光滑解适定性问题的研究成果较少. Chen, Du, Chen 和 Xin^[29]对于二维对称翼形面问题, 证明了有旋亚音速解的存在性和唯一性. 对于无旋不可压缩 Euler 方程, 二维的情况可由复变函数的经典理论讨论, 空间维数大于等于三的情况由 Ou^[30] 通过变分法证明了解的存在性和唯一性.

在适定性的基础上, 对于无界区域, 一个自然的问题就是研究解在无穷远处的渐近收敛速率. Du, Xie 和 Xin^[17]研究了二维可压 Euler 方程管道问题有旋解的无穷远的渐近收敛速率. Ma 和 Xie^[31]考虑了高维 ($n\geq 3$) 可压 Euler 方程管道问题无旋解的无穷远的渐近收敛速率. Ma^[32]在漩涡速度 $W=0$ 的情况下得到了三维柱对称可压 Euler 方程有旋解的无穷远的渐近收敛速率. 值得指出的是: Ma^[32]的结果在文献[22-23]的条件的基础上需要两个额外的条件.

对于三维柱对称定常非齐次不可压 Euler 方程管道问题解的适定性和无穷远渐近速率的研究主要有以下三个困难: 第一, 方程的解可能在对称轴附近出现奇性, 对应于流线在对称轴附近可能会分叉, 特别是在管道中放置障碍物的情况; 第二, 当涡旋速度 $W\neq 0$ 时, 漩涡速度会产生离心力, 可能导致流场出现静止或回流; 第三, 边界的角点会影响解的正则性. 针对困难一, 首先我们在对称轴附近引入比较函数, 证明方程在对称轴附近不会出现奇性; 再证明水平速度 $U>0$, 其中: 先证明无旋流的流线非退化性, 再通过估计有旋流和无旋流的差由连续性方法得到有旋流的流线不回流, 最后结合正负无穷远处的渐近行为和极大值原理得到流线的非退化性. 针对困难二, 本文引入了对于涡旋速度 $W$ 的流线守恒量 $rW$. 针对困难三, 我们在角点处构造了合适的闸函数, 利用极大值原理得到一致估计.

本文主要的创新点如下: 第一, 对于含有障碍物的三维柱对称管道问题, 首次证明了涡旋速度 $W \neq 0$ 的非齐次不可压 Euler 流解的适定性; 第二, 在两种边界条件下, 得到了无穷远的渐近收敛速率: 若无穷管道在有限长度以外是平边界, 则方程的解以指数速率收敛到渐近状态; 若无穷管道以多项式速率收敛到平边界, 则方程的解以相同的多项式速率收敛到渐近状态.

本文的章节安排如下: 第 2 节将三维柱对称齐次不可压 Euler 方程的无穷长管道问题转化为一个无界区域中非线性椭圆方程的边值问题并介绍本文的主要结果; 第 3 节证明解的适定性; 第 4 节讨论解在无穷远处的渐近收敛速率.

当流体是柱对称时, 即有

此时有

在柱对称轴上

速度分解如下

其中 $U$, $V$ 和 $W$分别是轴向速度, 径向速度和漩涡速度. 直接计算得到

不可压 Euler 方程的 Bernoulli 函数为

在柱对称坐标系下, 不可压 Euler 方程(1.1)变为

在 $(x,r)-$ 坐标系下, 管道的边界为

和

由(2.1)和(1.5)式得

其中 $\overrightarrow{n}$ 是 $\Gamma_{1}$ 上的单位外法向量. 滑动边界条件(1.5)变为

其中 $\overrightarrow{n}$ 是 $\Gamma_{2}\backslash\Pi$ 上的单位外法向量.

本文的主要结果包括适定性和无穷远渐近速率两部分. 适定性部分的定理陈述如下.

定理2.1 如果管道满足(1.2)-(1.5)式, 给定 $\left(W^{2}_-(r),U_-(r),\rho_-(r)\right)\in \left(C^{1,1}\left[1\right]\right)^{3}$ 满足如下条件

其中 $\delta$ 是依赖于 $U_-$ 和 $W_-^2$ 的正常数, 那么存在唯一的解 $(\rho, U, V, W,p)$, 其中 $(\rho, U, V, W^2,p)\in (C^{\alpha}(\overline{\Omega}) \cap C^{1,\alpha}(\Omega))^5$ 满足方程(2.2)和边界条件(2.3)以及(2.4)并且满足

(i) 流线不退化, 即

(ii) 当 $x\rightarrow \pm \infty$,

这里的 $\rho_{+},U_{+},W_{+},p_{+}$ 由 $\rho_{-},U_{-},W_{-},p_{-}$ 和 $m$ 唯一确定.

注2.1 此处的条件(2.5)为对称轴处的对称条件; 条件(2.6)为管道入口处密度和水平速度的正性条件; 条件(2.7)可推出流体轴向速度具有非负性, 从而保证流线在对称轴附近不出现分叉或者回流的条件; 条件(2.8)-(2.10)是为了保证解的唯一性以及渐近状态存在性唯一的条件. 对于不具有涡旋的齐次不可压Euler流, 即: $W_-=0$, $\rho=1$, 条件(2.6)-(2.10)可简化为轴向速度的凸性条件, 即

注2.2 此处的条件为: $W_-(r)^{2}\in C^{1,1}\left[1\right]$, 而不需要 $W_-(r)$ 是连续函数, 即允许存在间断点 $r_0\in(0, 1)$, 使得

对应于在 $\Omega$ 中存在一条 $C^{2, \alpha}$ 曲线 $\Gamma$, 其切线平行于 $(rU, rV)$. $\Gamma$ 将 $\Omega$ 划分为 $\Omega_+$ 和 $\Omega_-$, 使得

此类关于 $W(x, r)$ 的间断为一类特殊的接触间断, 可参考文献[18].

在适定性的基础上, 我们进一步的研究了解的无穷远渐近速率.

定理2.2 如果$W_-(r)$, $U_-(r)$ 和 $\rho_-(r)$ 满足定理2.1 中的条件,有如下两种情况

情况1 如果边界是在有限长度以外为平直, 即存在 $K>0$ 使得

那么存在 $C>0$, $\epsilon>0$ 和 $K^{'}> K$ 满足

情况2 如果边界以代数速率收敛到平直边界, 即 $f_1(x)$ 满足

那么存在 $C>0$ 和 $K^{'}>K$ 满足

其中 $\Omega_{x-1,x+1}=\Omega\cap\left[x-1,x+1\right]\times\left[1\right]$.

注2.3 值得注意的是, 相比于柱对称可压缩Euler方程已有的结果, 此定理可以包括漩涡速度 $W$ 不为 0 的情况, 并且在解的适定性条件基础上不需要添加额外的条件.

我们先假设 $V_-\equiv0$, 这将在命题3.2中证明. 当 $x\rightarrow-\infty$

和

给定的 $U_-(r)$, $\rho_-(r)$, $W_{-}(r)$, 那么 $B_{-}(r)$ 在入口处满足

由式$(2.2)_3$和 $V_-\equiv0$ 得

于是, $p_-$ 的表达式为

其中 $H_{-}(r)$=$\frac{\rho_{-}(r)W_-^{2}(r)}{r}$ 和 $p_{-c}$ 是任意常数表示在 $r=0$ 处的压力. 由 $(2.2)_4$ 式可知, 存在守恒量 $m$ 满足

流线守恒量来自于 Euler 方程组的线性退化部分

根据方程 $(2.25)_1$ 和 $\Omega$ 是单连通区域得, 存在一个流函数 $\psi$ : 满足

对于 $r\in (0, 1)$, 定义一个从 $\left[1\right]$ 到 $\left[m\right]$ 一一映射如下

令$ \kappa(m):=\psi^{-1}_{-}(m) $ 为 $\left[m\right]$ 到 $\left[1\right]$ 的一一映射. 直接计算得到

由于$(2.25)_2$-$(2.25)_4$ 式以及 $rW$, $B$ 和 $\rho$ 是流线守恒量, 于是, 当 $0\leq\psi\leq m$ 时,定义

因此, 得到

对式$(2.29)_3$ 关于 $x$ 求导得到

于是,

其中 $p$ 由下式给出

即

另一方面, 根据(2.26)式得到

因此, 我们得到关于 $\psi$ 的如下二阶方程

由边界条件(2.3)和(2.4), 得 $\psi$ 在 $\Gamma_1$和 $\Gamma_2$ 上分别都是常数, 即

因此, 将不可压 Euler 方程定值问题转化为关于 $\psi$ 的二阶方程的边值问题.

问题 1 求解如下边值问题

并且满足下列额外条件

令$\partial_1:=\partial_x$ 和$\partial_2:=\partial_r$. 将方程(2.33)写成非散度形式.

其中

本节中, 我们将求解问题1 即证明定理 2.1. 首先考虑没有边界没有角点的情况, 即 $\Gamma_1$ 和 $\Gamma_2$ 为 $C^{2, \alpha}$ 边界.

将 ${\cal G}(\psi)$, ${\cal B}(\psi)$ 和 ${\cal W}(\psi)$ 从 $[m]$ 延拓到 $\Bbb R$. 令

和

延拓后的函数如下

显然, $\tilde{{\cal G}}(s),\ \tilde{{\cal B}}(s),\ \tilde{{\cal W}^2}(s)\in C^{1,1}(\Bbb R)$. 当 $0\leq s\leq m$ 时, 直接计算得到

由式(2.7)得, 对于$0<s<m$

根据 $\tilde{{\cal G}}$, $\tilde{{\cal B}}$ 和 $\tilde{{\cal W}}^{2}$ 的定义得

当 $0<s<m$ 时, ${\cal K}(0,s,r)$严格大于$0$.

证 证明一共分为 4 步.

步骤1 考虑如下的逼近问题.

其中

$0<k\ll1$, $L \geq\max\{|L_1|,|L_2|\}$和

这里$\partial\Omega_{L}$ 是 $C^{2,\alpha_1}$ 边界, $0<\alpha_1<\alpha<1$, 并满足一致外球条件. 对于固定的 $k>0$ 和 $L>0$, 由文献[33]知,问题(3.6)存在唯一解 $\psi^{(k)}_L\in C^{2,H}(\Omega_L)\cap C^0(\bar{\Omega}_L)$.

步骤2 证明解在 $r=0$ 处不会有奇性. 通过式(3.5)得到

由强极大值原理得 $\psi^{(k)}_L$ 不能在内部取得极大极小值, 即在内部满足$0<\psi^{(k)}_L<m$. 这意味着 $\tilde{{\cal G}}={\cal G}$, $\tilde{{\cal B}}={\cal B}$ 和 $\tilde{{\cal W}}={\cal W}$. 令 $\phi(r)=\frac{m}{b^2}(r+k)^2$, 其中 $b=\inf\limits_{x\in\Bbb R}f(x)$. 如果存在一个临界点 $P_{\mbox{max}}=(x_0,r_0)$ 使得

那么在临界点处有

由式(3.5)和式(2.10)得

显然, 在边界上 $\psi^{(k)}_{L}\leq \frac{m}{b^2}(r+k)^2$. 因此, 通过比较原理得到

于是, 存在 $b>0$, 当 $k\rightarrow0$ 时, $\psi^{(k)}_{L}\rightarrow\psi_L$ 并满足

步骤3 证明流线非退化, 即 $U>0$.

首先考虑无旋流的非退化性. 对于无旋流, $\underline{B}$ 和 $\underline{G}$ 是分别取值于 ${\cal B}$ 和 ${\cal G}$ 值域的正常数, 以及漩涡速度 $W=0$. 当流体是无旋流, Euler 方程(2.2)变为

对应的 $\bar{\psi}_{L}$ 满足下列边值问题

由步骤2可知在 $\Omega^o$ 内 $0<\bar{\psi}_{L}<m$. 因为 $\bar{\psi}_{L}$ 在 $\Gamma_1\cap\partial\Omega_{L}$ 上有极小值, 利用 Hopf 引理得到

其中 $\eta$ 是 $\Omega_{L}$ 上的单位外法向量. 又因为 $\bar{\psi}_{L}$ 在 $\Gamma_1\cap\partial\Omega_{L}$ 等于0, 于是得到

因此,

这表明在 $\Gamma_1\cap\partial\Omega_{L}$ 上 $\partial_{2}\bar{\psi}_{L}>0$. 同理, 得到在其他边界上 $\partial_{2}\psi_{L}>0$, 即

根据 $U_r-V_x=0$, 得到一个位势函数 $\phi$ 满足

令 $\Phi\left(x_{1},x_{2},x_{3}\right)=\phi\left(x,r\right)$得

由不可压条件 $\mbox{div }u=0$ 得

关于 $x$ 求导可知

由(3.13)式, 利用强极大值原理得到在 $\overline{\Omega}_{L}$ 上 $U>0$.

接下来, 考虑有旋流的非退化性

结合(2.33)和(3.9)式得到

于是, $\phi$ 满足

因此, 对于任意的紧子集 $K\subset \Omega_{L}$, 如果 $\|({\cal G}',{\cal B}',{\cal W}')\|_{C^{0,1}([m])}\leq \delta$, 那么

这意味着

由于 $\partial_2\bar{\psi}_L>0$, 选择足够小的 $\delta$, 得到 $\partial_2\psi_L>0$. 假设存在最大的有界正数 $\delta_0$, 使得当 $\delta\leq\delta_0$ 时, $\partial_2\psi_L>0$; 当 $\|({\cal G}',{\cal B}',{\cal W}')\|_{C^{0,1}([m])}= \delta_0$ 时, 在某些点上 $\partial_2\psi_L\leq 0$. 那么通过选取一个序列 $({\cal G}_n, {\cal B}_n, {\cal W}_n)$, 其中对于每一个 $n\in \mathbb{N}$, $\|({\cal G}'_n,{\cal B}'_n,{\cal W}'_n)\|_{C^{0,1}([m])}\leq \delta_0$, 当 $n\rightarrow \infty$ 时, $({\cal G}_n, {\cal B}_n, {\cal W}_n)\rightarrow ({\cal G}, {\cal B}, {\cal W})$, 其中 $\|({\cal G}',{\cal B}',{\cal W}')\|_{C^{0,1}([m])}=\delta_0$. 记 $\psi_{L}^{(n)}$ 和 $\psi_L$ 分别是 $({\cal G}_n, {\cal B}_n, {\cal W}_n)$ 和 $({\cal G}, {\cal B}, {\cal W})$ 对应问题(3.6)的唯一解. 由有界区域解的唯一性和 $C^{2,\alpha}$ 估计, 当 $n\rightarrow\infty$ 得到 $\psi_{L}^{(n)}\rightarrow\psi_L$. 由 $\partial_2 \psi_{L}^{(n)}>0$, 可知 $\partial_2 \psi_{L}\geq0$. 由文献[34]可知如果 $\partial_2 \psi_{L}\geq0$, 那么 $\partial_2 \psi_{L}>0$, 与 $\delta_0$ 的定义矛盾. 因此, 不存在有界的 $\delta_0$. 从而, 对于任意的 $\delta>0$ 都有 $\partial_r \psi_{L}>0$.

步骤4 证明 $\psi_{L}$ 关于 $L$ 的一致估计.

利用文献[33,定理 3.7] 得

其中 $C={\rm e}^{\bar{f}}-1$. 因此

利用文献[33,引理 6.20], 存在 $C$ 满足

和

对于任意的紧子集 $K\in\bar{\Omega}$, 利用 Arzela-Ascoli 引理, $\{\psi_{L}\}$ 存在一个子列 $\psi_{L_n}$ 在 $C^{1,\alpha/2}(K)$ 意义下收敛到 $\psi$. 又因为 $\psi_{L}\in C^{2, \alpha}(\Omega)$. 显然, $\psi$ 是(4.22)的一个解且$\psi_r \geq 0$.证毕.

下面我们将利用能量估计证明解的唯一性.

命题3.1 给定$U_-(r)$, $\rho_-(r)$,$W_-(r)$ 满足定理 2.1 的假设, 那么问题 1的解是唯一的.

证 如果 $\psi_1$ 和 $\psi_2$ 都上述存在性结论的解, 即满足

令

直接计算得到 $\phi$ 满足

其中

取 $\eta\in C^{\infty}_0(\Bbb R)$ 满足: 当 $|s|<L$ 时, $\eta=1$; 当 $|s|>L+1$ 时, $\eta=0$. 将式(3.26)乘 $\eta^2(x)\phi$, 再在 $\Omega$ 上积分得

由分部积分得到

对于右端最后一项, 我们考虑 $ \widehat d$ 中积分内的项.

其中, 由流线守恒量与负无穷远处状态的关系有

对于 $I_{1}$,

由条件(2.8)和(2.10),有

由条件(2.9)得 $I_{2}\geq -\frac{\delta'}{4}$. 对于$I_{3}$ 和 $I_{4}$, 可由(2.10)条件控制. 综上可知: $ d\geq -\delta'$. 于是

结合 Hardy 不等式

和 Poincaré 不等式

以及 $\delta'$ 的小性, 我们可以得到: 对于任意 $L>0$,

因为 $\phi$ 在边界上等于0, 于是得, 在 $\Omega$ 上, $\phi= 0$, 即 $\psi_1=\psi_2$. 证毕.

命题3.2 对于$a_{B}>0$, 如果 $\bar{\psi}$ 是下列方程的解

其中 $D=\left\{\left(x,r\right)|x\in \left(-\infty,+\infty\right),r \in\left(0, a_B\right) \right\}$, 则在 $D$ 上 $\partial_x\bar{\psi}=0$.

证 任取 $x \in D$, 都有

如果 $\bar{\psi}$ 是方程(3.2)的解, 那么 $\bar{\psi}\left(x+\Delta x\right)$ 也是方程(3.2)的解. 根据命题3.1得到

因此, 在 $D$ 上 $\partial_x\bar{\psi}=0$.证毕.

令 $\psi$ 是问题 1 的解, 那么存在一个序列 $\psi^{(n)}=\psi\chi_{\{0<r<f(x-n)\}}$ 在 $C^{2,\vartheta}(K)$ 意义下收敛到 $\bar{\psi}_{-}$, 其中 $\bar{\psi}_{-}$ 满足: 对应于$a_B=1$ 的方程(3.29). 由(3.29)解的唯一性可知 $\bar{\psi}_{-}=\psi_{-}$. 结合命题 3.2 可知: $\partial_x\bar{\psi}_{-}=V_-\equiv0$, 并且, 当 $x\rightarrow - \infty$,

相似地, 存在一个序列 $\psi^{(n)}=\psi\chi_{\{0<r<f(x+n)\}}$ 收敛到 $\bar{\psi}_{+}$. $\bar{\psi}_{+}$ 满足: 对应于$a_B=a$ 的(3.29). 由(3.29)解的唯一性可知

由此可以确定, 当 $x\rightarrow +\infty$,

下面我们将证明 $U_{+}(r)>0$. 由已有的分析可以得到 $U_{+}(r)=\partial_r\bar{\psi}_{+}(r)\geq0$. 与式(3.13)类似, 利用 Hopf 引理, 得到 $U_+(0)>0$ 和 $U_+(a)>0$. 假设存在一点 $r_0\in\left(0,1\right)$ 使得 $ U_{+}(r_0)=0$, 那么$r_0$是 $ U_{+}(r)$的内部极小值点,由此可知$ \partial _r U_{+}(r_0)\leq 0$. $ \partial _r U_+={\cal K}\left(0,\bar{\psi}_{+},r\right). $ 由(3.5)得 $\partial _r U_{+}(r_0)>0$, 矛盾. 故 $U_{+}(r)>0$.

进一步的由极大值原理, 类似于文献[23], 我们可以得到在 $\Omega$ 上 $U(x, r)>0$. 由此对于 $f_1$ 和 $f_2$ 不具有角点的情况证明了定理1.

我们用一组光滑的边界去逼近角点附近的区域. 首先考虑下边界 $\Gamma_{2}$. 令 $\Omega^{\varepsilon}$ 是 $C^{2,\alpha}$ 边界, $r=f^{\varepsilon}_{2}(x)$ 的正则性取决于 $\varepsilon$. $\Omega^{\varepsilon}\subset\Omega$ 和 $f^{\varepsilon}_{2}(x)\rightarrow f_{2}(x)$, 并且存在足够大的 $X>0$ 满足对于任意的 $\varepsilon>0$ 和 $|x|\geq X$, 都有 $f^{\varepsilon}_{2}=f_{2}$. 不失一般性, 我们考虑角度为 $\theta_0$ 的角点 $P$, 这个区域为 $\Omega(R,\varepsilon):=\Omega^{\varepsilon}\cap B_R(P)$. 令 $\Gamma_{+}$ 和 $\Gamma_-$ 是 $P$ 点引出来的左右两条切线. 令 $(s,\theta)$ 是以 $P$ 为原点, $\Gamma_+$ 上 $\theta=0$ 的极坐标系. $\Gamma_-$ 上的角度为 $\theta_0\in(0,\pi)$. 记 $\theta_*=\frac{\pi-\theta_0}{2}$. 考虑如下闸函数

其中 $A\in(1,\frac{\pi+\theta_0}{2\theta_0})$, $C_1=\max(\csc\theta_*,\csc(A\theta_0+\theta_*))$, 和 $\beta\in(0, 1)$.

在 $\Omega^{\varepsilon}\cap \partial B_R(x_0)$, $\psi^{\varepsilon}\leq m\leq w$ 和在 $ B_R(x_0)\cap\partial\Omega_{\varepsilon}$, $\psi^{\varepsilon}=0\leq w$. 在 $\Omega^{\varepsilon}\cap B_R(x_0)$ 内, 当 $\beta$ 足够小时

通过极大值原理得到, 在 $\Omega(R,\varepsilon)$ 上

其中$C$ 是不依赖于 $\varepsilon$ 的常数. 利用标准的伸缩变换和 Schauder 估计, 得到 $\psi^{\varepsilon}$ 在 $C^{1,\beta}$ 意义下收敛 $\psi$. 显然, $\psi\in C^{1,\beta}$ 和 $|D\psi|\leq Cs^{\beta}$. 当角点出现在上边界时, 选择闸函数

可以得到相同的结论.

下面我们将证明解在无穷远处的渐进速率. 这里$\psi$ 是问题1的解,

$\psi_-$是问题(3.29)中$a_B$的解, 记

直接计算得到, 存在 $K^{'}>K$, 当 $x\le-K^{'}$ 时, $\Psi$ 满足

其中

令 $\eta(x,r)={\rm e}^{\mu r+\epsilon x}$, 其中 $\mu$ 和 $\epsilon$ 是正常数, 对 $\eta$ 作用 $L_0$ 得

令 $\mu$ 足够小, 有 $\mu-\frac{1}{r}\leq -\frac{1}{2}$. 令 $\epsilon$ 足够小, 有 $\epsilon^{2}+\mu\left(\mu-\frac{1}{r}\right)\leq -\frac{\mu}{4}$. 由 ${\cal D}>0$, 令 $\mu$ 足够小, 有 $-\mu r{\cal C}_{2}-r{\cal D}\leq \frac{\mu}{8}$. 于是,

令 $\nu={\rm e}^{\mu r}$, 同理得

令 $K_{2}$ 是一个常数且 $K_{2}>K_{1}$, 存在一个常数 $ C_0$ 满足

对于任意固定的 $\beta>0$, 存在 $s_0<K_1$ 满足

注意到

因此, 对于任意的 $s<s_0$, 满足

利用极大值原理得

由 $s$ 的任意性得

相似地, 存在一个常数 $C_1>0$ 满足

于是, 对于任意的 $\beta>0$,

这里的 $C_2=\max \{ {C_0},{C_1}\} $. 由 $\beta$ 的任意性得

于是

因此

令 $\Upsilon(x,r)=|-x|^{-l}{\rm e}^{\mu r}$. 其中 $ \mu$ 是正常数. 直接计算得到

令 $\mu$ 足够小和 $|x|$ 足够大得

记 $\hat{ f} =\min \{ {1},{f_2(x)}\} $ 和 $\hat{\Omega}=\{(x,r)| 0\le r \le \hat{f}\}$. 于是, 存在足够大的 $J_2>J_1$, 当 $x<-J_2$, 得

令 $J_3$ 是一个大于$J_2$ 的常数, 存在常数 $C$ 满足

对于任意的 $\beta>0$, 存在 $s_1<-J_3$ 满足

于是, 对于任意的 $s\le s_1$, 得

相似地, 我们得到

由 $\beta$ 和 $s$ 的任意性得

于是, 存在 $C>0$ 满足

因此,