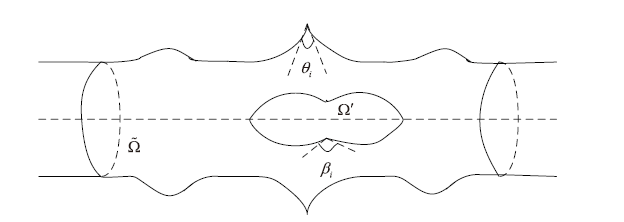
数学物理学报 ›› 2023, Vol. 43 ›› Issue (1): 219-237.
三维柱对称定常非齐次不可压 Euler 方程管道问题解的适定性及无穷远渐近速率
- 武汉理工大学理学院数学系 武汉430070
-
收稿日期:2022-05-13修回日期:2022-08-05出版日期:2023-02-26发布日期:2023-03-07 -
通讯作者:*王天怡, E-mail:tianyiwang@whut.edu.cn -
作者简介:林杰, E-mail:linjie@whut.edu.cn -
基金资助:国家自然科学基金(11971307)
Well-Posedness and Convergence Rates of Three-Dimensional Incompressible Euler Flows in Axisymmetric Nozzles with Symmetric Body
- Department of Mathematics, School of Science, Wuhan University of Technology, Wuhan 430070
-
Received:2022-05-13Revised:2022-08-05Online:2023-02-26Published:2023-03-07 -
Supported by:The NSFC(11971307)
摘要:
该文针对可以包含障碍物的三维柱对称无穷管道问题, 运用流函数方法转化为椭圆方程的边值问题, 利用能量估计和闸函数方法, 证明了定常非齐次不可压 Euler 方程解的存在性和唯一性以及流线的非退化性即
中图分类号:
- O175.2
引用本文
林杰, 王天怡. 三维柱对称定常非齐次不可压 Euler 方程管道问题解的适定性及无穷远渐近速率[J]. 数学物理学报, 2023, 43(1): 219-237.
Lin Jie, Wang Tianyi. Well-Posedness and Convergence Rates of Three-Dimensional Incompressible Euler Flows in Axisymmetric Nozzles with Symmetric Body[J]. Acta mathematica scientia,Series A, 2023, 43(1): 219-237.
使用本文
| [1] | Badiani T V. Existence of steady symmetric vortex pairs on a planar domain with an obstacle. Mathematical Proceedings of the Cambridge Philosophical Society, 2000, 132(2): 365-384 |
| [2] | Burton G R. Steady symmetric vortex pairs and rearrangements. Proceedings of the Royal Society of Edinburgh Section a Mathematics, 1988, 108(3/4): 269-290 |
| [3] | Burton G R. Variational problems on classes of rearrangements and multiple configurations for steady vortices. Annales De Linstitut Henri Poincare, 1989, 6(4): 295-319 |
| [4] |
Elcrat A R, Miller K G. Steady vortex flows with circulation past asymmetric obstacles. Communications in Partial Differential Equations, 1987, 12(10): 1095-1115
doi: 10.1080/03605308708820520 |
| [5] | Miller E. Rearrangements in steady vortex flows with circulation. Proceedings of the American Mathematical Society, 1991, 111(4): 1051-1055 |
| [6] |
Ambrosetti A, Struwe M. Existence of steady vortex rings in an ideal fluid. Archive for Rational Mechanics and Analysis, 1989, 108(2): 97-109
doi: 10.1007/BF01053458 |
| [7] |
Cao D M, Liu Z, Wei J. Regularization of point vortices for the Euler equation in dimension two. Archive for Rational Mechanics and Analysis, 2012, 212(1): 179-217
doi: 10.1007/s00205-013-0692-y |
| [8] |
Cao D M, Peng S J, Yan S. Planar vortex patch problem in incompressible steady flow. Advances in Mathematics, 2015, 270: 263-301
doi: 10.1016/j.aim.2014.09.027 |
| [9] |
Berger M S, Fraenkel L E. Nonlinear desingularization in certain free-boundary problems. Communications in Mathematical Physics, 1980, 77(2): 149-172
doi: 10.1007/BF01982715 |
| [10] |
Li G, Yan S, Yang J. An elliptic problem related to planar vortex pairs. SIAM Journal on Mathematical Analysis, 2005, 36(5): 1444-1460
doi: 10.1137/S003614100343055X |
| [11] |
Ni W M. On the existence of global vortex rings. Journal D'analyse Mathématique, 1980, 37(1): 208-247
doi: 10.1007/BF02797686 |
| [12] | Bers L. Mathematical Aspects of Subsonic and Transonic Gas Dynamics. New York: John Wiley and Sons, 1958 |
| [13] |
Xie C J, Xin Z P. Global subsonic and subsonic-sonic flows through infinitely long nozzles. Indiana University Mathematics Journal, 2007, 56(6): 2991-3023
doi: 10.1512/iumj.2007.56.3108 |
| [14] |
Xie C J, Xin Z P. Global subsonic and subsonic-sonic flows through infinitely long axially symmetric nozzles. Journal of Differential Equations, 2010, 248(11): 2657-2683
doi: 10.1016/j.jde.2010.02.007 |
| [15] |
Du L L, Xin Z P, Yan W. Subsonic flows in a multi-dimensional nozzle. Archive for Rational Mechanics and Analysis, 2011, 201(3): 965-1012
doi: 10.1007/s00205-011-0406-2 |
| [16] |
Xie C J, Xin Z P. Existence of global steady subsonic Euler flows through infinitely long nozzles. SIAM Journal on Mathematical Analysis, 2010, 42(2): 751-784
doi: 10.1137/09076667X |
| [17] |
Du L L, Xie C J, Xin Z P. Steady subsonic ideal flows through an infinitely long nozzle with large vorticity. Communications in Mathematical Physics, 2014, 328(1): 327-354
doi: 10.1007/s00220-014-1951-y |
| [18] |
Chen G Q, Huang F M, Wang T Y, et al. Steady Euler flows with large vorticity and characteristic discontinuities in arbitrary infinitely long nozzles. Advances in Mathematics, 2019, 346: 946-1008
doi: 10.1016/j.aim.2019.02.002 |
| [19] |
Du L L, Duan B. Global subsonic Euler flows in an infinitely long axisymmetric nozzle. Journal of Differential Equations, 2011, 250(2): 813-847
doi: 10.1016/j.jde.2010.06.005 |
| [20] |
Duan B, Luo Z. Three-dimensional full Euler flows in axisymmetric nozzles. Journal of Differential Equations, 2013, 254(7): 2705-2731
doi: 10.1016/j.jde.2013.01.008 |
| [21] |
Duan B, Luo Z. Subsonic non-isentropic Euler flows with large vorticity in axisymmetric nozzles. Journal of Mathematical Analysis and Applications, 2015, 430(2): 1037-1057
doi: 10.1016/j.jmaa.2015.05.023 |
| [22] | Duan B, Weng S K. Global smooth axisymmetric subsonic flows with nonzero swirl in an infinitely long axisymmetric nozzle. Ztschrift für angewandte Mathematik und Physik, 2018, 69(5): 1-17 |
| [23] |
Deng X M, Wang T Y, Xiang W. Three-dimensional full Euler flows with nontrivial swirl in axisymmetric nozzles. SIAM Journal on Mathematical Analysis, 2018, 50(3): 2740-2772
doi: 10.1137/16M1107991 |
| [24] | Shiffman M. On the existence of subsonic flows of a compressible fluid. Journal Rational Mechanics Analysis, 1952, 1: 605-652 |
| [25] |
Bers L. Existence and uniqueness of a subsonic flow past a given profile. Communications on Pure and Applied Mathematics, 1954, 7(3): 441-504
doi: 10.1002/cpa.3160070303 |
| [26] |
Bers L. Results and conjectures in the mathematical theory of subsonic and transonic gas flows. Communications on Pure and Applied Mathematics, 1954, 7(1): 79-104
doi: 10.1002/cpa.3160070107 |
| [27] |
Finn R, Gilbarg D. Three-dimensional subsonic flows and asymptotic estimates for elliptic partial differential equations. Acta Mathematica, 1957, 98(1): 265-296
doi: 10.1007/BF02404476 |
| [28] | 董光昌. 空间亚音速流及此边值问题在更高维情况的推广. 浙江大学学报, 1979, 1: 33-63 |
| Dong G C. Three-dimensinal subsonic ows and their boundary value problems extended to higher dimensions. Journal of Zhejiang University, 1979, 1: 33-63 | |
| [29] |
Chen C, Du L L, Xie C J, et al. Two dimensional subsonic Euler flows past a wall or a symmetric body. Archive for Rational Mechanics and Analysis, 2016, 221(2): 559-602
doi: 10.1007/s00205-016-0968-0 |
| [30] | Ou B. An irrotational and incompressible flow around a body in space. Journal of Partial Differential Equations, 1994, 7(2): 160-170 |
| [31] | Ma L, Xie C. Existence and optimal convergence rates of multi-dimensional subsonic potential flows through an infinitely long nozzle with an obstacle inside. Journal of Mathematica Physics, 2020, 61(7): 1-23 |
| [32] | Ma L. The optimal convergence rates of non-isentropic subsonic Euler flows through the infinitely long three-dimensional axisymmetric nozzles. Mathematical Methods in the Applied Sciences, 2020, 48(10): 6553-6565 |
| [33] | Gilbarg D, Trudinger N. Elliptic Partial Differential Equations of Second Order. Berlin: Springer, 1983 |
| [34] |
Chen G Q, Deng X M, Xiang W. Global steady subsonic flows through infinitely long nozzles for the full Euler equations. SIAM Journal on Mathematical Analysis, 2012, 44(4): 2888-2919
doi: 10.1137/11085325X |
| [1] | 陈兴发, 钟澎洪. 一般幂次散焦导数薛定谔方程解在Hs中的不适定性[J]. 数学物理学报, 2022, 42(6): 1768-1781. |
| [2] | 肖翔宇,蒲志林. Cahn-Hilliard-Brinkman系统的全局吸引子[J]. 数学物理学报, 2022, 42(4): 1027-1040. |
| [3] | 孟庆春,张磊. 一类三维逆时热传导问题的数值求解[J]. 数学物理学报, 2022, 42(1): 187-200. |
| [4] | 闵建中,刘宪高,刘子轩. 不可压液晶方程组的Serrin解[J]. 数学物理学报, 2021, 41(6): 1671-1683. |
| [5] | 赖柏顺,罗勍. 一类刻画微机电模型四阶抛物型方程解的适定性[J]. 数学物理学报, 2021, 41(6): 1718-1733. |
| [6] | 孙丹丹,李盈科,滕志东,张太雷. 具有年龄结构的麻疹传染病模型的稳定性分析[J]. 数学物理学报, 2021, 41(6): 1950-1968. |
| [7] | 西宣宣,侯咪咪,周先锋. 非自治Caputo分数阶发展方程弱解的适定性与不变集[J]. 数学物理学报, 2021, 41(1): 149-165. |
| [8] | 蔡钢. Banach空间上有限时滞退化微分方程的适定性[J]. 数学物理学报, 2018, 38(2): 264-275. |
| [9] | Marko Kostić, 李成刚, 李淼. 抽象多项Riemann-Liouville分数阶微分方程[J]. 数学物理学报, 2016, 36(4): 601-622. |
| [10] | 曲风龙, 李希亮. 各向同性的麦克斯韦方程的内部传输问题及反射参数的估计[J]. 数学物理学报, 2013, 33(6): 1178-1188. |
| [11] | 朱莉, 夏福全. 广义混合变分不等式的Levitin-Polyak适定性[J]. 数学物理学报, 2012, 32(4): 633-643. |
| [12] | 尹姝馨; 许跟起. 具有多重严重故障和非严重故障和修复功能的系统的可靠性分析[J]. 数学物理学报, 2007, 27(3): 392-413. |
| [13] | 倪仁兴. 广义共同逼近问题的适定性[J]. 数学物理学报, 2003, 23(2): 161-168. |
| [14] | 郭定辉. 一类广义层流方程组的初值问题的局部适定性[J]. 数学物理学报, 2001, 21(4): 433-438. |
| [15] | 刘康生. 非均质储层储量再估计的适定性[J]. 数学物理学报, 1996, 16(S1): 42-47. |
|