该文研究了如下具有非零边界条件的混合 Chen-Lee-Liu 导数非线性薛定谔方程的单极解和双极解,

方程(1.1)是 Kundu 在研究非线性薛定谔型方程的规范变换时首次得到的^[1]. 在光学领域, $|r|^2r$ 表示由光强引起的折射率的变化 ^[2], $|r|^2r_x$ 表示自陡峭效应. 在流体力学中,方程(1.1)可以从 Dysthe 方程中通过忽略平均流量项获得 ^[3]. 模型(1.1)用于描述非线性光纤和水波水槽中的实验现象 ^[4].

Hu 等^[5] 研究了半直线上(1.1)的初始边值问题. Zhang 等^[6] 通过 Darboux 变换得到了(1.1)的高阶解. 然后, Fang 等 ^[7] 得到了具有零边界条件的(1.1)的孤子解. 最近, Zhao 和 Fan ^[8] 通过 Riemann-Hilbert 方法研究了具有非零边界条件的(1.1)的多孤子解.

最近, 研究可积系统的孤子解已成为一个热门话题 ^[9⇓-11]. Zhang 和 Fan 通过 Riemann-Hilbert 方法获得了具有非零边界条件的薛定谔型方程的多孤子 ^[12]. Zhang 和 Yan 获得了具有零边界条件和非零边界条件的导数非线性薛定谔方程的孤子解 ^[13]. Zhang 和 Yan 研究了具有非零边界条件的聚焦和散焦 Hirota 方程的孤子解 ^[14].

据我们所知, 目前对于具有非零边界条件的方程(1.1)还没有人研究. 本文根据 Zhang 和 Yan ^[15] 的思想, 利用 Riemann-Hilbert 方法构造了方程(1.1)的单极解和双极解. 为了便于计算, 设非零边界条件如下

研究方程(1.1)在非零边界条件下的难点如下: 一方面, 在构造一个合适的黎曼曲面时, 为了避免特征值的多值情况, 需要引入了一个合适的均匀化变量; 另一方面, 在引入黎曼曲面后,方程(1.1)的逆散射将由原来的谱 $k$ -平面转化为新的变量 $z$ -平面, 难点在于建立两个平面之间的关系.

本文的其余部分组织如下. 在第 2 节中, 通过求解单极点的直散射问题, 得到了 Jost 解和散射矩阵的解析性、对称性、渐近性和离散谱性质. 在第 3 节中, 利用矩阵 Riemann-Hilbert 问题构造并解决了具有单极点的逆散射问题. 此外, 还得到了(1.1)的单极解. 在第 4 节中, 解决了具有双极点的直散射问题, 得到了相应的离散谱性质. 在第 5 节中, 研究了具有双极点的逆散射问题. 然后, 得到了(1.1)的双极解. 在第 6 节中, 给出了一些结论.

在直散射过程中, 为了避免特征值的多值性, 需要引入变量 $z=\lambda+k$. 通过求解直散射问题, 得到 Jost 解和散射矩阵, 并给出它们的解析性、对称性、渐近性和离散谱性质.

由文献[16] 知方程(1.1)的 Lax 对为

其中

为了将边界条件(1.2)变为常数边界，引入变换

方程(1.1)重新表示为

则方程(2.3)的 Lax 对为

其中

当 $x\rightarrow\pm\infty$ 时, 考虑(2.4)的渐近散射问题

其中

矩阵 $X_{\pm}$ 的特征值为 $\pm {\rm i}k\lambda$, $\lambda$ 满足 $\lambda^2=k^2+r_0^2$, 其分支点为 $k=\pm {\rm i}r_0$.

令

因此, 在 Riemann 曲面上得到两个单值解析函数

为了避免特征值 $\lambda$ 的多值情况, 现在定义一个均匀化变量 ^[17]

由此可得

因此, 可以用逆映射来讨论标准 $z$ 平面上的散射问题, 而不是在两张黎曼面上. 为了方便起见, 将 $z$ 平面上的 $D^+$、$D^-$ 和 $\Sigma$ 定义为

根据特征值 $\pm {\rm i}k\lambda$, 得到如下渐近特征向量矩阵

因此, $X_\pm$ 和 $T_\pm$ 可对角化为

经计算可得

将(2.7)式代入(2.5)式, 则

由此可得渐近谱问题(2.5)的解

其中 $\theta(x,t,z)=k(z)\lambda(z)\left[x+(-2k^2(z)+2+r_0^2)t\right]$.

Jost 解 $\phi_\pm(x,t,z)$ 有如下形式

令

则

此外, $\mu_\pm$ 满足如下关系

其中 $\Delta X_\pm=k(Q-Q_\pm)-\frac{\rm i}{4}(|r|^2-r_0^2)\sigma_3$, $\Delta T_\pm=T-T_\pm$. 上述方程可表示为

则 Volterra 积分方程为

命题2.1 设 $r(x,t)-r_\pm\in L^1({\Bbb R^\pm})$, Volterra 积分方程(2.13)有唯一解 $\mu_\pm(x,t,z)$, 它被(2.9)式定义在 $\Sigma_0:=\Sigma\backslash\{\pm {\rm i}r_0\}$ 上, 则 $\mu_\pm(x,t,z)$ 有如下性质

$\bullet$$\mu_{-,1}$ 和 $\mu_{+,2}$ 解析延伸到 $D^-$ 且连续延伸到 $D^-\cup \Sigma_0$.

$\bullet$$\mu_{+,1}$ 和 $\mu_{-,2}$ 解析延伸到 $D^+$ 且连续延伸到 $D^+\cup \Sigma_0$.

证 定义 $\mu_\pm= (\mu_{\pm,1}, \mu_{\pm,2})$, $W(x,z)=Y^{-1}_-\mu_-$, 则 $W$ 的第一列 $w$ 为

其中

因 ${\rm e}^{-2{\rm i}k\lambda(x-y)}={\rm e}^{-2{\rm i}(x-y){\rm Re}(k\lambda)}{\rm e}^{2(x-y){\rm Im}(k\lambda)}$, 而 $x-y>0$ 且 ${\rm Im}[k(z)\lambda(z)]<0$, 则 $\mu_{-,1}$ 解析延伸到 $D^-$. 类似地, 可以证明 $\mu_{-,2}$ 解析延伸到 $D^+$, $\mu_{+,1}$ 解析延伸到 $D^+$, $\mu_{+,2}$ 解析延伸到 $D^-$. 证毕.

推论2.1 设 $r(x,t)-r_\pm\in L^1({\Bbb R^\pm})$,(2.4)式有唯一解 $\phi_\pm(x,t,z)$, 它被(2.8)式定义在 $\Sigma_0$ 上, 则 $\phi_\pm(x,t,z)$ 有如下性质

$\bullet$$\phi_{-,1}$, $\phi_{+,2}$ 解析延伸到 $D^-$ 且连续延伸到 $D^-\cup \Sigma_0$.

$\bullet$$\phi_{+,1}$, $\phi_{-,2}$ 解析延伸到 $D^+$ 且连续延伸到 $D^+\cup \Sigma_0$.

由 Liouville 公式知 $\phi_\pm$ 是 Lax 对(2.5)的基解. 当 $z\in\Sigma_0$ 时, 定义常数散射矩阵 $S(z)=(s_{ij}(z))_{2\times2}$ 使得

其中 $s_{ij}(z)$ 为散射系数, 可表示为

其中 ${\rm Wr}(\cdot,\cdot)$ 表示 Wronskian 行列式.

根据(2.15)式和推论2.1, 有如下命题.

命题2.2 设 $r(x,t)-r_\pm\in L^1({\Bbb R^\pm})$, 散射系数 $s_{ij}(i,j=1,2)$ 有如下性质

$\bullet$$s_{11}(z)$ 解析延拓到 $D^+$ 且连续延拓到 $D^+\cup \Sigma_0$.

$\bullet$$s_{22}(z)$ 解析延拓到 $D^-$ 且连续延拓到 $D^-\cup \Sigma_0$.

$\bullet$$s_{12}(z)$, $s_{21}(z)$ 在 $z\in\Sigma_{0}$ 中连续.

为了解决逆散射问题中的矩阵 Riemann-Hilbert 问题, 需要势没有谱奇点. 假定 $s_{ij}(z)(i,j = 1,2)$ 在分支点 $\{\pm {\rm i}r_0\}$ 连续, 则反射系数定义为

为了研究逆散射问题中的离散谱和留数条件, 需要分析 Jost 解和散射矩阵 $S(z)$ 的对称性. 在 $z$ 平面中有两个对合：$z\rightarrow z^* $ 和 $z \rightarrow - \frac{r^2_0}{z}$, 它们在 $k$ 平面生成两个对合：$(k, \lambda) \rightarrow (k^*, \lambda^*)$ 和 $(k, \lambda) \rightarrow (k, -\lambda)$.

命题2.3 Jost 解、 散射矩阵和反射系数在 $z$ 平面有如下三种对称性质

$\bullet$ 第一对称性

其中 $ \sigma_{2}= \left( {\begin{array}{*{20}{c}} 0~&-{\rm i}\\ {\rm i}~&0 \end{array}} \right)$.

$\bullet$ 第二对称性

其中 $ \sigma_{1}= \left( {\begin{array}{*{20}{c}} 0~&1\\ 1~&0 \end{array}} \right). $

$\bullet$ 第三对称性

证 令 $\phi(x,t,z)$ 是散射问题(2.4)的一个解, 即

则

因

故

因此, $\sigma_2\phi^*(z^*)\sigma_2$ 也是散射问题(2.4)的一个解.

由如下关系

可得

由散射问题解的唯一性可得

即

类似地, 利用如下关系

可得 $\phi_{\pm}(x,t,z)$ 的第二对称性, 即

由此可知

接下来, 证明 $\phi_{\pm}(x,t,z)$ 的第三对称性. 若 $\phi_{\pm}(x,t,z)$ 是散射问题(2.4)的一个解, 利用如下关系

则对于任意与 $x$ 和 $t$ 无关的 $2\times2$ 矩阵 $C$, $\phi(x,t,-\frac{r_0^2}{z})C$ 也是散射问题(2.4)的一个解.

根据(2.8)式, 显然有

因

则 $C={\frac{\rm i}{z}}\sigma_3Q_\pm$, 于是

由此可知

接下来证明散射矩阵的对称性. 将(2.18)式的第一个式子带入(2.14)式, 可得

由此可知

于是

类似地, 可得 $S(z)=\sigma_1S^*(-z^*)\sigma_1$, 由此可知

于是

将(2.20)式的第一个式子带入(2.14)式, 可得

由此可知

于是

证毕.

散射问题的离散谱是所有 $z\in {\Bbb C}\backslash\Sigma$ 使得特征函数存在于 $L^2(\Bbb R)$ 上的值的集合. 设 $s_{11}(z)$ 在 $Z_0=\{z\in{\Bbb C}:{\rm Re}z>0,{\rm Im}z>0,|z|>r_0\}$ 中有 $N_{1}$ 个单极点 $z_{1},\cdots,z_{N_1}$, 在圆 $W_0=\{z=r_0{\rm e}^{{\rm i}\varphi}:0<\varphi<\frac{\pi}{2}\}$ 上有 $N_{2}$ 个单极点 $w_{1},\cdots,w_{m}$, 即 $s_{11}(z_n)=0$ 且 $s^\prime_{11}(z_n)\neq0$. 由散射矩阵的对称性知

且

则离散谱为

由于 $s_{11}(z_0)=0$, $z_{0}\in D^+$, 则存在一个常数 $b_+(z_0)$ 使得

由此可知

于是

其中 $A_+[z_0]={\frac{b_+(z_0)}{s^{'}_{11}(z_0)}}$.

由于 $s_{22}(z^*_0)=0$, $z^*_0\in D^-$, 则存在一个常数 $b_-(z^*_0)$ 使得

由此可知

于是

其中 $A_-[z^*_0]={\frac{b_-(z^*_0)}{s^{'}_{22}(z^*_0)}}$.

根据 $b_{\pm}[z_0]$ 和 $A_\pm[z_0]$ 的定义以及 Jost 解和散射矩阵的对称性, 有如下命题成立.

命题2.4 在 $Z$ 中, 留数条件系数之间有如下关系成立

证 将 $z=-z_n$ 带入(2.26)式, 由 Jost 解的对称性可得

因 $s_{11}(z)$ 是一个偶函数, 即 $s^{\prime}_{11}(-z_n)=-s_{11}^{\prime}(z_n)$, 则

类似地, 容易得到

由(2.27)式可得

合并(2.21)式有

比较(2.26)式, 可得 $b_+(z_n)=-b^*_-(z^*_n).$ 由(2.23)式可得 $ [s^{*}_{22}(z^*)]^{\prime}=s^{\prime}_{11}(z),$ 由此可知 $ A_+[z_n]=-A^*_-[z^*_n]. $ 类似地, 重复上述过程, 有 $ A_+[\omega_m]=-A^*_-[\omega^*_m]. $

将 $z=-{\frac{r^2_0}{z^*_n}}$ 带入(2.27)式, 根据 Jost 解的第三对称性知

类似地, 可得

由散射矩阵的第三对称性知

由此可知

类似地, 可得

合并上述关系, 可得

证毕.

为了提出和解决逆散射问题中 Riemann-Hilbert 问题, 需要分别讨论 Jost 解和散射矩阵在 $z\rightarrow \infty$ 和 $z\rightarrow0$ 的渐近性质. 利用标准的 Wentzel-Kramers-Brillouin 展式, 可以推导出 Jost 解的渐近性质.

命题2.5 Jost 解具有如下渐近性质

其中

证 考虑如下渐近展式

将上述表达式带入(2.11)式, 有

比较 $O(z^2)$ 项, 有 $ [\mu^{(0)}_\pm,\sigma_3]=0, $ 由此可知 $\mu^{(0)}_\pm$ 是一个对角矩阵. 将其记为

比较 $O(z)$ 项, 有

由此可知

其中 $\mu^{(1)}_{\pm,o}$ 是 $\mu^{(1)}_\pm$ 的次对角部分. 比较 $O(1)$ 项, 有

由此可知

其中

接下来, 考虑 Jost 解 $\mu_{\pm}(x,t,z)$ 在 $z\rightarrow 0$ 的渐近展式

同样地, 将(2.33)式带入(2.11)式, 有

其中 $C$ 是一个常数 $2\times2$ 矩阵. 由(2.33)和(2.10)式知

因此 $C={\rm i}\sigma_3Q_\pm$ 且 $\tilde{\mu}^{(-1)}_\pm={\rm i}{\rm e}^{{\rm i}\nu_\pm(x,t)\sigma_3}\sigma_3Q_\pm$. 证毕.

推论2.2 散射矩阵有如下渐近性质

其中

证 当 $z\rightarrow\infty$ 时, 有

其中

类似地, 可知

当 $z\rightarrow0$ 时, 有

且

证毕.

接下来, 借助广义矩阵 Riemann-Hilbert 问题来构造和求解逆问题. 此外, 给出了重构公式、迹公式和 $\theta$ 条件. 最后, 得到方程(1.1)的单极解.

为了将逆问题转换为广义矩阵 Riemann-Hilbert 问题, 需要对(2.14)式中的项进行重新排列, 沿着 $\Sigma$ 建立一个关系. 利用它们的渐近性质和 Plemelj 公式, 得到 Riemann-Hilbert 问题的解.

命题3.1 定义分段亚纯矩阵

可得如下 Riemann-Hilbert 问题

$\bullet$ 解析性: $M(x,t,z)$ 在 ${\Bbb C}\setminus\Sigma$ 解析且有单极点.

$\bullet$ 跳跃条件

其中

$\bullet$ 渐近性质

证 由 $\mu_\pm$ 和 $s_{ij}(z)$ 的解析性可得 $M(x,t,z)$ 的解析性. 此外, 由(2.14)式知

由此可得, 跳跃条件(3.3).

接下来, 证明 $M(x,t,z)$ 的渐近性质. 根据(3.1)式, 则 $M^+(x,t,z)$ 表示为如下形式, 当 $z\rightarrow\infty$, 有

当 $z\rightarrow0$, 有

利用类似的方法可得 $M^-(x,t,z)$ 的渐近性质. 证毕.

为了提出并解决 Riemann-Hilbert 问题, 定义

且 $\hat{\zeta}_n=-{\frac{r^2_0}{\zeta_n}}$, $n=1,2,\cdots,4N_1+2N_2$.

解决上述 Riemann-Hilbert 问题需要通过去除渐近行为和极点贡献来对其进行正则化

根据柯西算子和 Plemelj 公式, Riemann-Hilbert 问题的解写为如下形式

为了呈现一个封闭的代数系统, 需要计算在(3.5)式中留数的表达式. 在(3.1)式中 $M(x,t,z)$ 的定义表明, 只有 $M^+$ 的第一列在 $z = \zeta_n$ 处有极点, $M^-$ 的第二列在 $z =\hat{\zeta}_n$ 处有极点, 则在(3.5)式中的留数部分表示为

其中

对于 $z=\zeta_n \in D^+$, 计算 $M^+$ 的第二列, 有

接下来, 根据 Riemann-Hilbert 问题的解来构造势. 当 $z\rightarrow\infty$ 时,(3.5)式的渐近展式为

取 $M=M^+$, 比较矩阵(3.7)式在$ (1,2) $位置的元素, 则带有单极点势的重构公式为

回顾 $s_{11}(z)$ 在 $D^+$ 上解析, $s_{22}(z)$ 在 $D^-$ 上解析. 离散谱点 ${\zeta_n}$ 是 $s_{11}(z)$ 的单极点, ${\hat{\zeta}_n}$ 是 $s_{22}(z)$ 的单极点. 定义

由此可知, $\beta^+(z)$ 和 $\beta^-(z)$ 分别在 $D^+$ 和 $D^-$ 上解析且没有零点.

当 $z\rightarrow\infty$ 时, $\beta^\pm\rightarrow1$. 因此

取上式的对数并使用 Plemelj 公式, 有

于是, 迹公式为

当 $z\rightarrow0$ 时, 由(3.9)和(2.34)式知 $\theta$ 条件为

接下来, 考虑一类特殊的解, 即反散射系数 $\rho(z)=\tilde{\rho}(z)=0$. 在这种情况下, 有如下命题成立.

命题3.2 方程(1.1)在非零边界条件下的单极解可表示为

其中$M=(m_{kn})_{(4N_1+2N_2)\times(4N_1+2N_2)}$, $\beta=(\beta_k)_{ (4N_1+2N_2)\times1}$, $\alpha=(\alpha_n)_{(4N_1+2N_2)\times1}$,

证 由(2.20)式可知

将(3.13)式带入(3.6)式, 有

其中 $\delta_{kn}$ 表示 Kronecker delta 函数. 则

将(3.14)式带入(3.8)式, 得到(3.12)式. 证毕.

容易证明, 若 $r(x,t)$ 是方程的解, 对于任意的 $c \in \Bbb R$, $cr(x, t)$ 也是方程的解. 因此, 不失一般性, 令 $r_0= 1$. 通过(3.12)式, 可以得到具有非零边界方程(1.1)的单极解精确表达式.

$\bullet$ 令 $N_1=0,\ N_2=1, \ r_-=1, \ r_+={\rm e}^{{\rm i}(2\nu_0-4\beta)}, \ \omega_1={\rm e}^{{\rm i}\beta},\ A_-[\omega^*_1]={\rm e}^{{\rm i}\tau+\kappa}$, 则

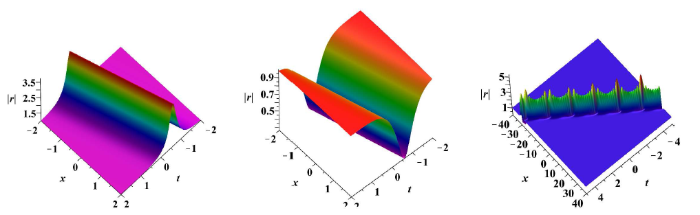
其中 $\nu_-=\frac{1}{4}\int_{-\infty}^x(|r|^2-r^2_0){\rm d}y$, $\varphi=\frac{(8t+2x)\sin(2\beta)}{2}+{\rm i}\tau-\frac{t\sin(4\beta)}{2}+\kappa$. 取参数 $\omega_1={\rm e}^{\frac{\pi}{6}{\rm i}}, A_-[\omega^*_1]={\rm i}$, 得到亮孤子(见图1 (左)), 取参数 $\omega_1={\rm e}^{\frac{\pi}{6}{\rm i}},\ A[\omega^*_1]=-{\rm i}$, 得到暗孤子 (见图1 (中)).

$\bullet$ 令 $N_1=1,\ N_2=0, \ r_-=1, \ r_+={\rm e}^{{\rm i}(2\nu_0-8\alpha)}, \ z_1=Z{\rm e}^{{\rm i}\alpha},\ Z>1, \ \alpha\in(0,\frac{\pi}{2}),\ A_-[z^*_1]={\rm e}^{\xi+{\rm i}\varphi}$. 特别地, 取参数 $z_1=2{\rm e}^{\frac{\pi}{3}{\rm i}}, A_-[z^*_1]={\rm i}$, 得到呼吸解的动力学结构 (见图1 (右)).

事实上, 反射系数 $\rho(z)$, $\tilde{\rho}(z)$ 可具有多个极点. 接下来, 考虑反射系数允许具有复数共轭离散谱对的双极点情况.

带有双极点的散射问题不同于单极点的情况. 一方面, 它们可以使分段亚纯矩阵函数 $M (x,t;z)$ 表现出不同类型的极点, 进一步使得 $M (x,t;z)$ 生成不同的势. 另一方面, 迹公式和 $\theta$ 条件也与单极点的情况不同.

设离散谱点 $z_0$ 是散射系数 $s_{11}(z)$ 和 $s_{22}(z)$ 的双零点, 即对于 $\forall z_0 \in D^+$, $s_{11}(z_0) = s^{\prime}_{11}(z_0) = 0$, $s^{\prime\prime}_{11}(z_0)\neq0$. 对于 $\forall z_0 \in D^-$, $s_{22}(z_0) = s^{\prime}_{22}(z_0) = 0$, $s^{\prime\prime}_{22}(z_0)\neq0$.

容易证明, 若 $f$ 和 $g$ 在 $\Omega\subset{\Bbb C}$ 区域上解析, $g$ 在 $z_0\in\Omega$ 上有一个双极点且 $f(z_0)\neq0$, 则当 $z =z_0$ 时, $f/g$ 的 Laurent 展开式的主部分系数为

其中 $\mathop{{\rm Res}}\limits_{z=z_0}\left[f(x,t,z)\right]$ 和 $\mathop{P_{-2}}\limits_ {z=z_0}\left[f(x,t,z)\right]$ 分别表示 $f(x,t,z)$ 在 $z=z_0$ 的 Laurent 级数展开项 $O((z-z_0)^{-1})$, $O((z-z_0)^{-2})$的系数.

由 $z_0$ 为 $s_{11}$ 的双极点, 可得

存在一个常数 $d_n$ 使得

利用(2.26),(4.2)和(4.1)式, 有

其中 $A_+[z_0]={\frac{2b_+[z_0]}{s^{\prime\prime}_{11}(z_0)}}$, $B_+[z_0]={\frac{d_+(z_0)}{b_+(z_0)}-\frac{s^{\prime\prime\prime}_{11}(z_0)} {3s^{\prime\prime}_{11}(z_0)}}$, $ z_0 \in Z \cap D^+$.

由 $z^*_0$ 为 $s_{22}$ 的双极点, 可得

利用(2.26),(4.1)和(4.4)式, 有

其中 $A_-[z_0]={\frac{2b_-[z^*_0]}{s^{\prime\prime}_{22}(z^*_0)}}$, $B_-[z^*_0]={\frac{d_-(z^*_0)}{b_-(z^*_0)}-\frac{s^{\prime\prime\prime}_{22}(z^*_0)} {3s^{\prime\prime}_{22}(z^*_0)}}$, $ z^*_0 \in Z \cap D^-$.

命题4.1 对于 $n=1,2,\cdots,N_1$, $m=1,2,\cdots,N_2$, 有

证 根据命题 2.4, 利用 $A_\pm[z_0]$ 和 $B_\pm[z_0]$ 的定义, 可以证明命题. 详细的证明也可以参考文献[10].

与单极点类似, 通过求解广义的矩阵 Riemann-Hilbert 问题, 得到了重构公式、迹公式和 $\theta$ 条件. 另外, 给出了方程(1.1)的双极解.

命题 3.1 中的 Riemann-Hilbert 问题仍适用于双极情况. 要解决这类 Riemann-Hilbert 问题, 必须消除渐近性质和奇点贡献

利用柯西算子和 Plemelj 公式, 可以得到带有双极点的 Riemann-Hilbert 问题的解

为了进一步表示 Riemann-Hilbert 问题的解, 需要计算 $P_{-2} (\cdot)$ 和 Res $(\cdot)$. 利用(4.3)和(4.5)式, 有

其中

接下来, 需要计算 $\mu^\prime_{-,2}(\zeta_n)$, $\mu_{-,2}(\zeta_n)$, $\mu^\prime_{-,1}(\hat{\zeta}_n)$, 和 $\mu_{-,1}(\hat{\zeta}_n)$.(5.1)式的第二列表示为

将(2.22)式的第二个方程带入(5.3)式, 令 $z=\zeta_k$, $k=1,2,\cdots,4N_1+2N_2$, 则

取 $\mu_{-,2}(z)$ 关于 $z$ 的一阶导数, 则

由(2.22)式可得

将(5.5)式带入(5.4)式, 令 $z=\zeta_k$, $k=1,2,\cdots,4N_1+2N_2$, 则

根据 Riemann-Hilbert 的解来构造势. 当 $z\rightarrow\infty$ 时,(5.1)式的渐近展式为

取 $M=M^+$, 比较矩阵(5.6)在 $(1,2)$ 位置的元素, 则带有双极点势的重构公式为

定义

容易证明 $\beta^+(z)$ 和 $\beta^-(z)$ 分别在 $D^+$ 和 $D^-$ 上解析且没有零点. 当 $z \rightarrow\infty$ 时, $\beta^\pm(z)\rightarrow 1$. 则

利用柯西算子和 Plemelj 公式, 可得

则迹公式为

当 $z\rightarrow0$ 时, 考虑(5.7)和(2.34)式, 则 $\theta$ 条件为

命题5.1 方程(1.1)在非零边界条件下的双极解可表示为

其中

定义 $H$ 为 $(8N_1+4N_2)\times(8N_1+ 4N_2)$ 矩阵

当 $N=1$ 时,(5.9)式中双极解的表达式非常复杂, 因此没有明确给出. 然而, 在软件 Maple 的帮助下, 通过取不同参数, 得到的相应动力学结构.

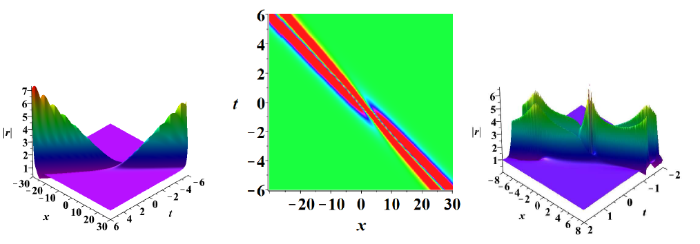
$\bullet$ 取 $N_1=0,\ N_2=1, \ r_-=1, \ r_+={\rm e}^{{\rm i}(2\nu_0-8\beta)}, \ \omega_1={\rm e}^{ i\beta}, \ A_-[\omega^*_1]={\rm e}^{{\rm i}\tau_1+\kappa_1},\ B_-[\omega^*_1]={\rm e}^{{\rm i}\tau_2+\kappa_2}$, 图2 (左, 中) 分别展示了双极解的三维图和密度图.

$\bullet$ 取 $N_1=1,\ N_2=0, \ r_-=1, \ r_+={\rm e}^{{\rm i}(2\nu_0-16\alpha)},\ z_1=Z{\rm e}^{{\rm i}\alpha},\ Z>1,\ \alpha\in(0,\frac{\pi}{2}), \ A_-[z^*_1]={\rm e}^{{\rm i}\xi_1+\varphi_1},\ B_-[z^*_1]={\rm e}^{{\rm i}\xi_2+\varphi_2}$. 图2 (右) 描述了带有相同速度的两个呼吸解之间的相互作用.

该文研究了在无穷远处方程(1.1)在非零边界条件下的单极解和双极解. 通过解决直散射问题, 得到了 Jost 解和散射矩阵的解析性、对称性、渐近性和离散谱. 逆问题是建立在矩阵 Riemann-Hilbert 问题的基础上. 最后, 得到了方程(1.1)的单极解和双极解公式, 并通过图形分别展示了他们的动力学行为. 近年来, 关于方程解的长时间渐近行为的研究已成为一个热门话题. 今后, 将继续研究具有非零边界条件的方程(1.1)的长时间渐近行为.