1 引言
设
许多作者提出并分析了几种迭代方法来求解变分不等式问题(1.1). 其中最简单的是如下的投影梯度算法[6]
其中
为求解单调且Lipschitz连续的变分不等式问题, Korpelevich[7]提出了外梯度算法, 迭代如下
但外梯度算法有两个缺点, 其一是需要在两个不同的点上计算映射
Popov在有限维欧氏空间中证明了该算法的收敛性.
为了克服第二个缺点, Censor, Gibali和Reich[14]提出了次梯度外梯度算法
这里
设
其中映射
Nadezhkina和Takahashi[22]提出了如下迭代算法
其中映射
2011年, Censor, Gibali和Reich[14]提出如下迭代算法
其中映射
算法1.1
初始化 给定
迭代步骤
第一步 令
这里
第二步 计算
这里
第三步 计算
若
其中映射
2021年, Cai, Dong和Peng[19]引进了求解变分不等式问题的新的粘性外梯度算法, 其迭代格式如下.
算法1.2
初始化 给定
迭代步骤
第一步 计算
若
第二步 计算
这里
这里
第三步 计算
令
其中映射
受上述思想的启发, 本文引进了一个新的惯性次梯度外梯度算法, 并结合粘性算法, 在一定条件下, 我们证明了这一算法所产生的序列强收敛于伪单调变分不等式问题解集与拟非扩张映射的不动点集合的公共元素.
2 预备知识
在这一节, 我们回顾一下本文所需的定义和引理.
映射
若
任给
其中
下面给出投影的一些基本性质, 可详见文献[29, 命题3.5, 定理3.6].
引理2.1 设
(1)
(2)
映射
映射
映射
映射
映射
映射
映射
设
为了证明主要定理, 我们需要下述引理.
引理2.2[30] 设
引理2.3[31] 设
引理2.4[32] 设
事实上
引理2.5[33] 给定
引理2.6[34] 设
3 算法及其收敛性分析
在这一节中, 我们为求解伪单调变分不等式问题, 引入了一类新的带惯性的粘性次梯度外梯度方法. 为引入算法, 我们需要下述条件.
条件3.1 映射
条件3.2
条件3.3 设
和
现在引进下述算法.
算法3.1
初始化 给定
迭代步骤
第一步 令
这里
第二步 计算
这里
第三步 计算
且
若
注3.1 算法3.1中的步长选择与算法1.1 (即文献[18, 算法1])的步长选择不同. 准确地说, 我们的步长选择更优. 事实上, 算法1.1中的Armijo -型线搜索规则为
对(3.7)式不等号左右两边同乘
又由Cauchy-Schwartz不等式, 有
结合(3.8)和(3.9)式得
即算法3.1中的(3.2)式成立.
注3.2 最近, 文献[35]用了一个新的步长规则修改了次梯度外梯度法, 即
这里要求
为了证明本文的主要定理, 我们先证明下述引理.
引理3.1 假定条件3.1–3.3成立, 则Armijo-型线搜索规则(3.2)有意义.
证 若
现在考虑
由Cauchy-Schwartz不等式知
且由均值不等式有
结合(3.10)–(3.12)式, 我们有
从而
于是
考虑下述两种情形.
情形1 假设
从而
由条件3.1知,
由(3.15), (3.16)式知(3.13)式是矛盾的.
情形2 假设
再由条件3.1知,
结合(3.14)和(3.18)式得
令
即
于是
对(3.20)式取极限, 令
从而
引理3.2 假设条件3.1–3.3成立, 设
证 因为
则
即
或者等价写成
下证
考虑两种情形.
情形1 假设
情形2 假设
因为
所以
由Armijo-型线搜索规则(3.2)式, 有
即
由Cauchy-Schwartz不等式知
且由均值不等式有
结合(3.25)–(3.27)式得
从而
故
结合(3.24)和(3.28)式, 得
另外, 由
变形后有
在(3.30)式中令
因此, (3.22)式成立. 注意到
由
在(3.31)式中令
最后, 证明
并且, 对每个
设
由
从而
下证
事实上, 由
由
则
由于
则
由引理2.2得,
引理3.3 假设条件3.1–3.3成立,
证 由
因为
于是
注意到
由
由(3.35), (3.37)–(3.39)式知
故结论得证.
引理3.4 假定条件3.1–3.3成立, 若
证 设
因为
则
从而
所以
另外一方面, 若
故
定理3.1 假设条件3.1–3.3成立,
证 (1) 先证明
由
由(3.40)和(3.41)式得
由
由于
由(3.42)和(3.44)式得
由
由归纳法得
故
(2) 下证, 存在
事实上, 由
其中
则
由(3.44)式, 得
其中
则
其中
(3) 下证, 存在
事实上, 由
其中
因此
(4) 最后, 证明序列
情形1 存在
且
由(3.53)和(3.55)式, 得
由
结合(3.56)和(3.57)式, 得
另外, 注意到
由
由于
由
由(3.60)和(3.62)式, 得
在(3.52)式中利用引理2.3得,
情形2 存在
在这种情形下, 利用引理2.4, 存在
由(3.49)式有
这表明
用情形1的证明方法, 得
且
利用(3.52)式, 得
这表明
利用(3.64)式, 得
因此,
注3.4 定理3.1在以下几个方面推广和改进了Thong和Hieu[18]的定理3.1.
(i) 将
(ii) 在适当的参数条件下, 我们得到了一个新的强收敛定理. 然而文献[18, 定理3.1]获得弱收敛性.
注3.5 当
4 数值实验
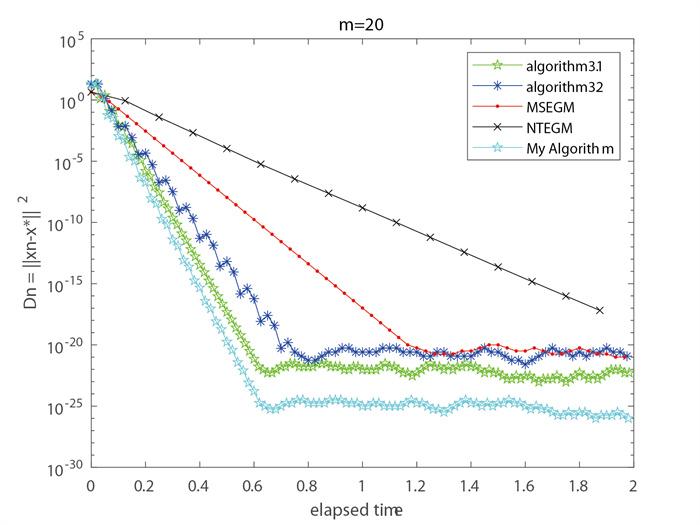
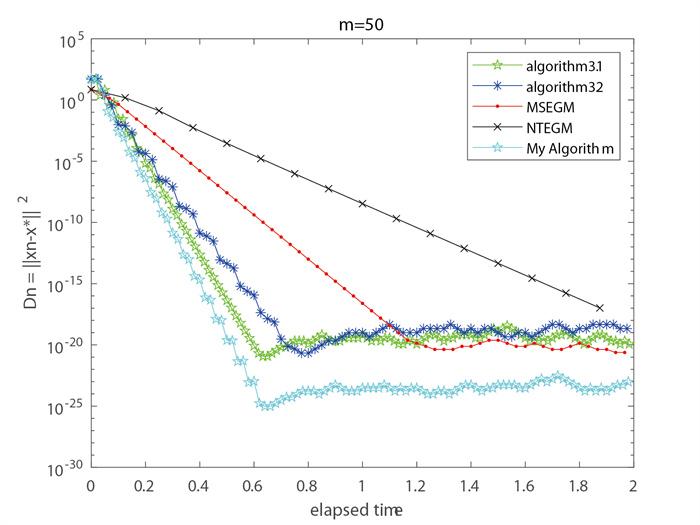
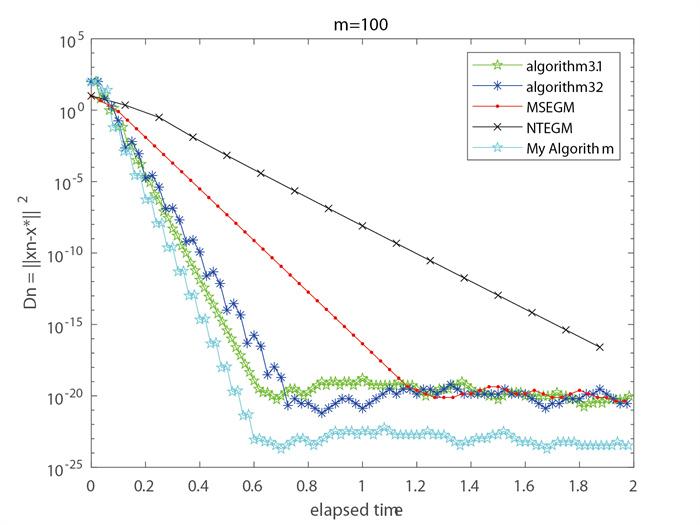
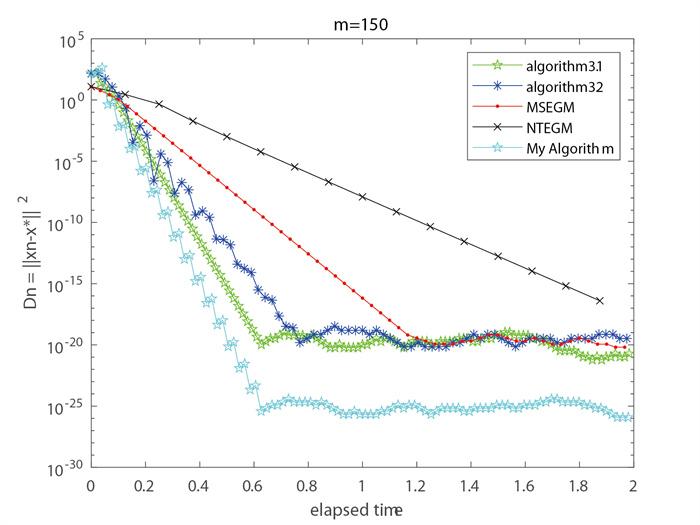
例1 设
显然,
对于本次数值实验, 初始点
算法3.1:
对于文献[22]中的NTEGM算法:
对于文献[13]中的MSEGM算法:
对于文献[18]中的算法3.1和算法3.2:
图 1
图 2
图 3
图 4
参考文献
Complementarity problems over cones with monotone and pseudomonotone maps
Methodes iteratives pour les equations et inequations aux derivees partielles non lineares de type monotone
The extragradient method for finding saddle points and other problems
Modified extragradient methods for variational inequality problems and fixed point problems for an infinite family of nonexpansive mappings in Banach spaces
DOI:10.1007/s10898-012-9883-6 [本文引用: 1]
A new double-projection method for solving variational inequalities in Banach spaces
Korpelevich's method for variational inequality problems in Banach spaces
Modified extragradient methods for a system of variational inequalities in Banach spaces
Single projection algorithm for variational inequalities in Banach spaces with application to contact problem
A modification of the Arrow-Hurwicz method for the search of saddle points
The subgradient extragradient method for solving variational inequalities in Hilbert space
DOI:10.1007/s10957-010-9757-3 [本文引用: 2]
Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems
Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems
Strong convergence theorems for nonexpansive mappings and inverse strongly monotone mappings
Inertial subgradient extragradient algorithms with line-search process for solving variational inequality problems and fixed point problems
DOI:10.1007/s11075-018-0527-x [本文引用: 8]
Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators
DOI:10.1007/s10957-020-01792-w [本文引用: 4]
Fixed point theorems in partially ordered Banach spaces with applications to nonlinear fractional evolution equations
DOI:10.1007/s11784-016-0316-x [本文引用: 1]
Weak convergence theorems for nonexpansive mappings and monotone mappings
DOI:10.1023/A:1025407607560 [本文引用: 1]
Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings
DOI:10.1007/s10957-005-7564-z [本文引用: 4]
Subsequential limit points of successive approximations
An inertial Popov's method for solving pseudomonotone variational inequalities
DOI:10.1007/s11590-020-01599-8 [本文引用: 1]
An inertial Tseng's type proximal algorithm for nonsmooth and nonconvex optimization problems
求解伪单调变分不等式问题的惯性收缩投影算法
DOI:10.3969/j.issn.1003-3998.2021.06.026
An inertial contraction and projection algorithm for pseudomonotone variational inequality problems
DOI:10.3969/j.issn.1003-3998.2021.06.026
Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings
An inertial method for solving split common fixed point problems
DOI:10.1007/s11784-017-0464-7 [本文引用: 1]
Pseudo-monotone complementarity problems in Hilbert space
DOI:10.1007/BF00941468 [本文引用: 1]
Iterative algorithm for nonlinear operators
DOI:10.1112/S0024610702003332 [本文引用: 1]
The viscosity approximation process for quasi-nonexpansive mapping in Hilbert space
DOI:10.1016/j.camwa.2009.09.003 [本文引用: 1]
Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators
DOI:10.1007/s10559-015-9768-z [本文引用: 1]
Inexact versions of proximal point and augmented Lagrangian algorithms in Banach spaces
DOI:10.1081/NFA-100105310 [本文引用: 1]
Self-adaptive inertial subgradient extragradient algorithm for solving pseudomonotone variational inequalities
DOI:10.1080/00036811.2019.1634257 [本文引用: 1]
A damped-Newton method for the linear complementarity problem
A new projection method for variational inequality problems
DOI:10.1137/S0363012997317475 [本文引用: 1]