1 引言
本文研究求解一类时间分数阶B-S期权定价模型的MQ拟插值新方法.
在分数阶B-S期权定价理论方面, 许多学者做了大量工作, 例如文献[3, 5] 提出了空间分数阶模型, 文献[4, 15] 发展了时间分数阶模型, 文献[11–12] 则研究时空分数阶模型.然而, 各种分数阶B-S模型的解析解都很复杂, 一般很难求出, 因此需要发展数值解. 许多数值求解分数阶B-S方程的算法已经被发展起来了, 例如文献[4, 16] 给出了一些关于分数阶B-S模型的数值算法, 但是这些算法都是基于有限差分等网格类方法, 对网格具有很强的依赖性, 难以处理期权价格因在行权价附近变化剧烈、需要维持较多的配置点以达到准确模拟的要求.因此, 科研界亟需探索构造无网格的求解分数阶B-S模型的新途径.
本文将借助三阶MQ拟插值, 构造求解时间分数阶B-S模型的新算法, 算法不仅是无网格的, 而且计算稳定、具有较高精度.
给定序列
其中当
其中
这里
这里
本文的结构如下. 在第二节, 我们构造了具有空间
2 求解时间分数阶B-S模型的三阶MQ拟插值方法
2.1 时间分数阶B-S模型
其中
令
这里
2.2 时间分数阶B-S模型的三阶MQ拟插值格式
将区间
其中
根据三阶MQ拟插值(0.1)式, 有
进一步, 根据文献[13], 函数的一阶和二阶导数具有逼近形式
将上述
其中
舍掉截断误差, 取
设
这里
以及
则, (2.6)式具有矩阵形式
3 三阶MQ拟插值方法的稳定性和收敛性
设
这里
设
这里
设
进一步可得
假设
将(3.3)式带入(3.1)式, 可得
(Ⅰ) 当
等价地
注意到函数
因此,
(Ⅱ) 当
(1)
(2)
命题3.1 对任何
证 由
这就意味着
定理3.1 MQ拟插值格式(2.6)是无条件稳定的.
证 应用(3.2)式和命题3.1, 得
即三阶MQ拟插值格式是无条件稳定的. 证毕.
由文献[13, 定理2]简单修改可得出下面定理.
定理3.2 三阶MQ拟插值格式是
4 数值结果
对于给定数据点
选择径向基函数为
以下是Matlab 2010的运算结果, 实验是在一个装有8 GB RAM和2.70 GHz速度的Inter Core i5笔记本电脑上完成的.
例4.1 考虑模型
这里
满足精确解表达式
设
它们相应的收敛速度分别列于表 1和表 2. 这里
表 1 N=1000时的空间后验误差估计
| α | M | L2 | rate (L2) | L∞ | rate (L∞) |
| 0.7 | 4 | 6.732 × 10−3 | 7.821 × 10−3 | ||
| 8 | 1.587 × 10−3 | 2.09 | 1.784 × 10−3 | 2.13 | |
| 16 | 2.986 × 10−4 | 2.41 | 3.366 × 10−4 | 2.42 | |
| 32 | 3.867 × 10−5 | 2.95 | 4.586 × 10−5 | 2.87 | |
| 64 | 3.225 × 10−6 | 3.58 | 4.133 × 10−6 | 3.47 | |
| 0.3 | 4 | 6.851 × 10−3 | 8.070 × 10−3 | ||
| 8 | 1.613 × 10−3 | 2.09 | 1.882 × 10−3 | 2.10 | |
| 16 | 3.055 × 10−4 | 2.40 | 3.541 × 10−4 | 2.41 | |
| 32 | 4.012 × 10−5 | 2.93 | 4.630 × 10−5 | 2.93 | |
| 64 | 3.396 × 10−6 | 3.56 | 3.895 × 10−6 | 3.57 |
表 2 M=100时的时间方向后验误差估计
| α | N | L2 | rate (L2) | L∞ | rate (L∞) |
| 0.7 | 10 | 3.124 × 10−3 | 4.301 × 10−3 | ||
| 20 | 1.351 × 10−3 | 1.27 | 1.847 × 10−3 | 1.22 | |
| 40 | 5.240 × 10−4 | 1.28 | 7.403 × 10−4 | 1.31 | |
| 80 | 2.142 × 10−4 | 1.32 | 2.854 × 10−4 | 1.37 | |
| 160 | 8.096 × 10−5 | 1.33 | 1.009 × 10−4 | 1.48 | |
| 0.3 | 10 | 3.670 × 10−3 | 4.984 × 10−3 | ||
| 20 | 1.142 × 10−3 | 1.68 | 1.583 × 10−3 | 1.66 | |
| 40 | 3.560 × 10−4 | 1.69 | 4.871 × 10−4 | 1.69 | |
| 80 | 1.084 × 10−4 | 1.71 | 1.494 × 10−4 | 1.71 | |
| 160 | 3.330 × 10−5 | 1.74 | 4.447 × 10−5 | 1.74 |
表 3 例4.1, 形状参数c敏感性分析, M=32, N=1000
| c | α = 0.7 | α = 0.3 | ||
| L2 | L∞ | L2 | L∞ | |
| 0.1 | 5.987 × 10−5 | 8.344 × 10−5 | 6.783 × 10−5 | 9.045 × 10−5 |
| 0.2 | 3.867 × 10−5 | 4.586 × 10−5 | 4.012 × 10−5 | 4.630 × 10−5 |
| 0.3 | 4.637 × 10−5 | 6.690 × 10−5 | 6.532 × 10−5 | 8.046 × 10−5 |
| 0.4 | 5.450 × 10−5 | 7.098 × 10−5 | 6.998 × 10−5 | 8.993 × 10−5 |
| 0.5 | 6.721 × 10−5 | 9.873 × 10−5 | 7.356 × 10−5 | 9.567 × 10−5 |
| 0.6 | 7.983 × 10−5 | 1.032 × 10−4 | 8.220 × 10−5 | 1.356 × 10−4 |
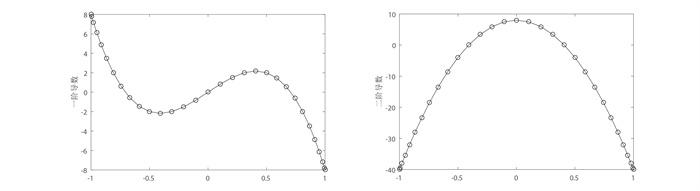
图 1
例4.2 考虑如下系统
其中
满足精确解表达式
选取
图 2
表 4 例4.2, 形状参数c敏感性分析, M=21, N=1000
| c | α=0.7 | α=0.3 | ||
| L2 | L∞ | L2 | L∞ | |
| 0.73 | 9.332 × 10−5 | 1.437 × 10−4 | 1.230 × 10−4 | 3.877 × 10−4 |
| 0.63 | 2.173 × 10−5 | 3.245 × 10−5 | 3.875 × 10−5 | 4.690 × 10−5 |
| 0.53 | 2.356 × 10−4 | 3.678 × 10−4 | 3.256 × 10−4 | 4.730 × 10−4 |
| 0.43 | 5.889 × 10−4 | 7.356 × 10−4 | 6.709 × 10−4 | 9.034 × 10−4 |
| 0.33 | 1.853 × 10−3 | 2.801 × 10−3 | 2.089 × 10−3 | 3.903 × 10−3 |
| 0.23 | 4.743 × 10−2 | 6.082 × 10−2 | 6.044 × 10−2 | 9.871 × 10−2 |
5 结论
本文运用三阶MQ拟插值方法求解时间分数阶B-S期权模型. 借助傅立叶分析, 验证了算法的稳定性和收敛性. 无论是均匀点还是非均匀点, 数值结果都能有较好的模拟效果. 将这种方法应用于时间分数阶的障碍期权、回望期权和其他奇异期权的求解是我们以后要研究的课题.
参考文献
Multiquadric B-Splines
DOI:10.1006/jath.1996.0089 [本文引用: 3]
The pricing of options and corporate liabilities
The finite moment log stable process and option pricing
DOI:10.1111/1540-6261.00544 [本文引用: 1]
Derivatives pricing with marked point processes using tick-by-tick data
DOI:10.1080/14697688.2012.661447 [本文引用: 2]
Fractional diffusion models of option prices in markets with jumps
Analytically pricing European-style options under the modified BlackScholes equation with a spatial-fractional derivative
DOI:10.1090/S0033-569X-2014-01373-2 [本文引用: 2]
On choosing "optimal" shape parameters for RBF approximation
A robust kernel-based solver for variable-order time fractional PDEs under 2D/3D irregular domains
DOI:10.1016/j.aml.2019.02.025 [本文引用: 1]
A new fractional numerical differention formula to approximate the Caputo fractional derivative and its applications
DOI:10.1016/j.jcp.2013.11.017 [本文引用: 2]
Adaptive moving knots meshless method for simulating time dependent partial differential equations
DOI:10.1016/j.enganabound.2018.08.010 [本文引用: 1]
Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton's optimal portfolio
DOI:10.1016/j.camwa.2009.05.015 [本文引用: 1]
The solutions to a bi-fractional Black-Scholes-Merton differential equation
Approximation to the k-th derivatives by multiquadric quasi-interpolation method
DOI:10.1016/j.cam.2009.05.017 [本文引用: 4]
Shape preserving properties and convergence of univariate multiquadric quasi-interpolation
DOI:10.1007/BF02016334 [本文引用: 2]
Numerical solution of the time fractional Black-Scholes model governing European options
A multiquadric quasi-interpolations method for CEV option pricing model