1 引言
其中
这表明
2019年, Segawa和Suzuki [14]研究了一般Hilbert空间
2 预备知识
本节主要回顾一些关于量子Bernoulli噪声的基本概念和事实. 此外, 为便于应用, 本节也引述了Segawa和Suzuki在文献[14]中建立的谱映射定理.
2.1 量子Bernoulli噪声
设
以
其中
其中
其中
显然
对每个非负整数
其中
算子
由文献[1] 可知, 量子Bernoulli噪声满足如下等时典则反交换关系(CAR) 和其它运算关系
且
其中
2.2 Segawa-Suzuki谱映射定理
以下, 若
设
引理2.1[14] 令
其中
注2.1 设

3 主要结果
本节将给出本文的主要结论. 为便于后续证明, 先给出一些必要的技术性命题. 回想
命题3.1 设
证 显然
因此
这意味着
如前所示, 算子
命题3.2 设
则
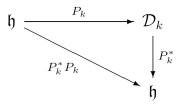
证 显然
于是
故
命题3.3 设
特别地,
证 对满足
此即
结合命题3.1可得
另一方面, 容易看出
对任意的
由此可得下一个有用的命题.
命题3.4 设
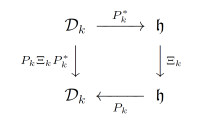
下一个定理为本文的第一个主要结果, 其中精确给出了
定理3.1 设
其中
证 考虑算子
这意味着
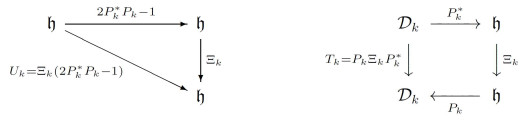
由引理2.1知
其中
其中
同样由于
根据引理2.1, 命题3.3及命题3.4可得
又
由上述定理可知, 算子
命题3.5 设
证 设
此式连同
反之, 对任意
此式连同
综上可得
命题3.6 设
证 (反证法) 假设
这蕴含着
这等价于(3.11)式.
由上述讨论可知, 对于
定理3.2 设
证 由命题3.5和命题3.6立得.
定理3.3 设
证 令
这表明
类似地可证明
4 应用
设
所以函数
定义4.1 设
则称
命题4.1
证 令
由此可知, 对一切
命题4.2 设
证 根据定理3.2, 不妨假定
故
这表明, 对一切
由命题4.1及4.2知,
参考文献
Discrete-time quantum Bernoulli noises
DOI:10.1063/1.3431028 [本文引用: 2]
Invariant states for a quantum Markov semigroup constructed from quantum Bernoulli noises
DOI:10.1142/S1230161218500191 [本文引用: 1]
Quantum Feller semigroup in terms of quantum Bernoulli noises
Quantum Bernoulli noises approach to Stochastic Schrödinger equation of exclusion type
Weighted number operators on Bernoulli functionals and quantum exclusion semigroups
DOI:10.1063/1.5120102 [本文引用: 1]
Open quantum random walk in terms of quantum Bernoulli noise
Stein's method and stochastic analysis of Rademacher functionals
Higher-dimensional open quantum walk in environment of quantum Bernoulli noises
Higher-dimensional quantum walk in terms of quantum Bernoulli noises
Normal approximation and almost sure central limit theorem for non-symmetric Rademacher functionals
DOI:10.1016/j.spa.2016.09.002 [本文引用: 1]
A new limit theorem for quantum walk in terms of quantum Bernoulli noises
DOI:10.3390/e22040486 [本文引用: 1]
Quantum walk in terms of quantum Bernoulli noises
Spectral mapping theorem of an abstract quantum walk
DOI:10.1007/s11128-019-2448-6 [本文引用: 3]
直线上空间非齐次三态量子游荡的平稳测度
The stationary measure of a space-inhomogeneous three-state quantum walk on the line
时间非齐次二态量子游荡的演化过程分析
DOI:10.3969/j.issn.1003-3998.2021.04.017 [本文引用: 1]
The analysis of evolution process in a time-inhomogeneous two-state quantum walk
DOI:10.3969/j.issn.1003-3998.2021.04.017 [本文引用: 1]
一类无界算子的二次数值域和谱
DOI:10.3969/j.issn.1003-3998.2020.06.002
The quadratic numerical range and the spectrum of some unbounded block operator matrices
DOI:10.3969/j.issn.1003-3998.2020.06.002


