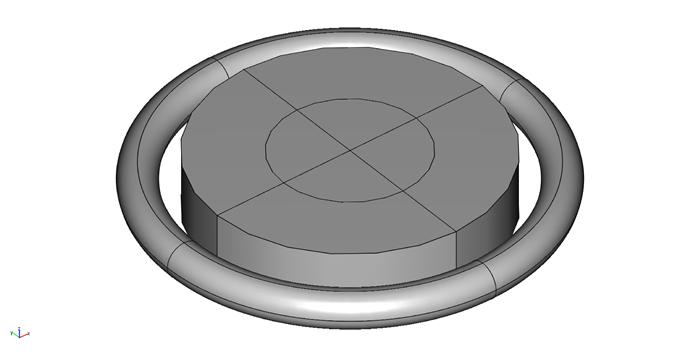
电磁感应加热是一种非接触的加热导体材料的方法, 该方法常用于工业应用中, 例如金属硬化和锻造预热. 感应加热系统的基本组成包括感应线圈(电感器), 交流电源和工件(见图 1). 交变电流通过电感器会产生交变磁场, 该磁场使工件产生涡流, 从而耗散涡流的能量并产生焦耳热. 关于感应加热系统的研究, 通常依赖于一系列复杂, 昂贵且漫长的实验, 因此, 数学理论分析和数值模拟可以在设计感应加热过程中发挥重要作用.

感应加热模型由Maxwell方程和热传导方程组成. 对于线性电磁材料, 文献[1–3, 17]提出了各种数值计算方案, 文献[4, 7, 9, 10, 19–21]研究了耦合问题的适定性并给出了理论结果. 据我们所知, 很少有同时考虑非线性关系$ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{B}} ( \mathit{\boldsymbol{H}} )$和电导率依赖于温度函数的研究. 例如, 文献[16]研究了导体中基于非线性$ \mathit{\boldsymbol{H}} $的耦合系统, 并讨论了其可解性. 文献[6, 11]研究了区域中包含导体和非导体部分的非线性模型, 给出了模型的矢量—标量势公式. 这些文献仅涉及对非线性感应加热问题时间半离散格式的研究. 目前为止, 很少有文献研究全离散有限元方法.

本文的目的是对非线性感应加热问题提出全离散$ \mathit{\boldsymbol{H}} $有限元方法, 讨论全离散格式解的收敛性. 文章组织结构如下: 第二章将建立非线性感应加热模型; 第三章给出基于$ \mathit{\boldsymbol{H}} $形式的时间半离散格式和一些收敛结果; 第四章提出全离散有限元解耦格式, 证明全离散格式解的存在唯一性, 给出稳定性估计; 第五章将讨论全离散格式解的收敛性. 最后, 给出数值实验来支持理论结果.

下面考虑一个简化的感应加热模型. $ \Omega\subset{\Bbb R}^3 $是一个带有连续边界$ \partial\Omega $的区域, 被电磁材料所填充. 电磁场方程由涡流方程描述

(2.1) $ \begin{equation} \left\{ \begin{array}{ll} & \partial_t\mathit{\boldsymbol{B}} + \nabla \times\mathit{\boldsymbol{E}} =0, \\ & \nabla \times\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{J}}+\mathit{\boldsymbol{J}}_s, \end{array} \right. \end{equation} $

其中$ \mathit{\boldsymbol{E}} $是电场, $ \mathit{\boldsymbol{H}} $是磁场, $ \mathit{\boldsymbol{B}} $是磁通密度, $ \mathit{\boldsymbol{J}}_s $是$ \Omega $外部电感器中的源电流密度. 假设$ \mathit{\boldsymbol{J}}_s $是无散度的, 那么一个交变磁场$ \mathit{\boldsymbol{H}}_s $使得

$ \mathit{\boldsymbol{J}}_s=\nabla \times\mathit{\boldsymbol{H}}_s. $

使用Biot-Savart定律可以直接计算出$ \mathit{\boldsymbol{H}} _s $如下

$ \mathit{\boldsymbol{H}}_s(\mathit{\boldsymbol{x}}, t): =\frac{1}{4\pi} \int_{\Omega} \frac{\mathit{\boldsymbol{J}}_s(\mathit{\boldsymbol{y}}, t)\times (\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}})}{|\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}}|^3} {\rm d}\mathit{\boldsymbol{y}}, $

这里的$ \Omega $是一个足够大的关于$ \mathit{\boldsymbol{y}} $的积分区域. 假设集合$ \{ \mathit{\boldsymbol{y}}: \mathit{\boldsymbol{J}}_s \not\equiv {\bf{0}} \} $到边界$ \partial \Omega $的距离足够远, 使得$ \mathit{\boldsymbol{H}}_s $在$ \partial \Omega $上近似满足$ \mathit{\boldsymbol{H}}_s \times \mathit{\boldsymbol{n}} = {\bf{0}} $. 交变磁场在$ \Omega $中产生涡流, 即$ \mathit{\boldsymbol{J}}=\sigma\mathit{\boldsymbol{E}} $, 其中电导率$ \sigma = \sigma(u) $依赖于温度函数$ u $. $ \sigma $是严格正的且有界, 即存在正的常数$ \sigma_* $和$ \sigma^* $, 使得

(2.2) $ \begin{equation} 0<\sigma_*\leq \sigma(s)\leq \sigma^*<\infty, \; \; s>0. \end{equation} $

引入$ \sigma $的反函数$ \gamma $, 同样$ \gamma $也是有界的, 即$ 0 <\gamma_*\leq \gamma\leq \gamma^*<\infty $.

研究$ \Omega $中$ \mathit{\boldsymbol{H}} $与$ \mathit{\boldsymbol{B}} $之间呈非线性关系的这类模型是至关重要的. 此外, 铁磁体的磁化曲线具有单调性. $ \mathit{\boldsymbol{B}} $与$ \mathit{\boldsymbol{H}} $之间的非线性关系为$ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}) $. 假设矢量场$ \mathit{\boldsymbol{B}} $为有势场, Lipschitz连续的和严格单调的. 仿照文献[18], 定义$ \mathit{\boldsymbol{B}} $的势为$ \Phi_{\mathit{\boldsymbol{B}}} $, 即$ \mbox{grad}\; \Phi_{{\mathit{\boldsymbol{B}}}}=\mathit{\boldsymbol{B}} $, 满足下列条件

(2.3) $ \begin{equation} \begin{array}{ll} (\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{y}}))\cdot (\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}})\geq b_*|\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}}|^2, \; \; b_*>0\; \; \; \; \; &\forall\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}\in {\Bbb R}^3, \\ \mathit{\boldsymbol{B}}{({\bf{0}})}={\bf{0}}, \\ \mathit{\boldsymbol{B}}^{-1}(\mathit{\boldsymbol{x}})\cdot(\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}})\geq \Phi_{\mathit{\boldsymbol{B}}^{-1}}(\mathit{\boldsymbol{x}})-\Phi_{\mathit{\boldsymbol{B}}^{-1}}(\mathit{\boldsymbol{y}})&\forall\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}\in{\Bbb R}^3, \\ \Phi_{{\mathit{\boldsymbol{B}}}^{-1}}(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}}))\geq C_0|\mathit{\boldsymbol{x}}|^2 &\forall\mathit{\boldsymbol{x}}\in{\Bbb R}^3. \end{array} \end{equation} $

由$ \mathit{\boldsymbol{B}} $的严格单调性可知, $ \mathit{\boldsymbol{B}} $为可逆的, $ \mathit{\boldsymbol{B}}^{-1} $是Lipschitz连续的. 根据文献[18, 定理5.1], $ \mathit{\boldsymbol{B}} $的势$ \Phi_{\mathit{\boldsymbol{B}}} $是严格凸的. 由文献[18, 定理8.4]得到

(2.4) $ \begin{equation} \begin{array}{ll} \mathit{\boldsymbol{B}}^{-1}(\mathit{\boldsymbol{x}})\cdot(\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}})\geq \Phi_{\mathit{\boldsymbol{B}}^{-1}}(\mathit{\boldsymbol{x}})-\Phi_{\mathit{\boldsymbol{B}}^{-1}}(\mathit{\boldsymbol{y}})\hskip 1cm \forall\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}\in{\Bbb R}^3, \end{array} \end{equation} $

(2.5) $ \begin{equation} \frac{\rm d}{{\rm d}t}\Phi_{{\mathit{\boldsymbol{B}}}^{-1}}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}})\big)={\mathit{\boldsymbol{B}}}^{-1}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}})\big)\cdot \frac{{\rm d}\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}})}{{\rm d}t}=\mathit{\boldsymbol{x}}\cdot \frac{{\rm d}\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{x}})}{{\rm d}t}. \end{equation} $

考虑下述磁场的初始边值问题

(2.6) $ \begin{equation} \left\{ \begin{array}{ll} \partial_t\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}'+\mathit{\boldsymbol{H}}_s) + \nabla \times\big(\gamma(u)\nabla \times\mathit{\boldsymbol{H}}'\big) = {\bf{0}} & \; (\mathit{\boldsymbol{x}}, t)\in \Omega\times (0, T), \\ \mathit{\boldsymbol{H}}'\times\mathit{\boldsymbol{n}}={\bf{0}} & \; (\mathit{\boldsymbol{x}}, t)\in \partial\Omega\times (0, T), \\ \mathit{\boldsymbol{H}}'(0) = \mathit{\boldsymbol{H}}_0 & \; \mathit{\boldsymbol{x}}\in \Omega, \; t=0, \end{array} \right. \end{equation} $

其中$ {\mathit{\boldsymbol{n}}} $为$ \partial\Omega $上的单位外法线向量. 初值$ \mathit{\boldsymbol{H}}_0 $在$ \partial \Omega $上满足$ \mathit{\boldsymbol{H}}_0 \times \mathit{\boldsymbol{n}} = {\bf{0}} $.

本文主要研究如何求解$ \mathit{\boldsymbol{H}}' $. 为了简便起见, 下述内容依然使用$ \mathit{\boldsymbol{H}} $代替$ \mathit{\boldsymbol{H}}' $.

由于$ \mathit{\boldsymbol{B}} $的散度为零, 设

$ \nabla \cdot\mathit{\boldsymbol{B}}\big(\mathit{\boldsymbol{H}}(0)+\mathit{\boldsymbol{H}}_s(0)\big) = 0 \hskip 1cm \; \; \mathit{\boldsymbol{x}}\in \Omega. $

$ \Omega $中电流产生的局部焦耳热为

$ \begin{array}{ll} \mathit{\boldsymbol{J}}\cdot\mathit{\boldsymbol{E}}=\gamma(u)|\nabla \times\mathit{\boldsymbol{H}}|^2 & \; \; (\mathit{\boldsymbol{x}}, t)\in\Omega\times (0, T). \end{array} $

为了处理热传导方程中的焦耳热项, 对其引入截断函数^[16]

$ {\cal R}_r (x) := \left\{ \begin{array}{ll} \; r, \hskip 1cm & \; \; x>r, \\ \; x, \hskip 1cm & \; \; |x|\leq r, \\ -r, \hskip 1cm & \; \; x<-r, \end{array} \right. $

其中$ r $是正的常数. 温度函数$ u $的变化由下面带有初始条件和边界条件的热传导方程表示

(2.7) $ \begin{equation} \left\{ \begin{array}{ll} \partial_t u-\nabla \cdot(\lambda\nabla u)={\cal R}_r\big(\gamma(u)|\nabla \times\mathit{\boldsymbol{H}}|^2\big) & \; (\mathit{\boldsymbol{x}}, t)\in \Omega\times (0, T), \\ { } -\lambda\frac{\partial u}{\partial\mathit{\boldsymbol{n}}}=0 & \; (\mathit{\boldsymbol{x}}, t)\in \partial\Omega\times (0, T), \\ u(0)=u_0& \; \; \mathit{\boldsymbol{x}}\in \Omega, \; t=0, \end{array} \right. \end{equation} $

其中导热系数$ \lambda(\mathit{\boldsymbol{x}}, t) $是严格正的, 有界的$ (0<\lambda_*\leq \lambda\leq \lambda^*<\infty) $, 满足

(2.8) $ \begin{equation} |\lambda(\mathit{\boldsymbol{x}}, t_2)-\lambda(\mathit{\boldsymbol{x}}, t_1)|\leq C_\lambda|t_2-t_1|\hskip 0.5cm \forall\mathit{\boldsymbol{x}}\in\Omega, \; \forall t_1, t_2\in[0, T]. \end{equation} $

通过(2.6)式中的$ \gamma(u) $项和(2.7)式中的焦耳热项, 磁场方程和热传导方程被耦合在一起.

首先, 给出一些贯穿全文的概念和符号. 定义$ L^2(\Omega) $空间的內积及范数

$ (u, v):= \int_\Omega u(\mathit{\boldsymbol{x}})v(\mathit{\boldsymbol{x}}) {\rm d}\mathit{\boldsymbol{x}}, \; \; \|u\|:=\sqrt{(u, u)}. $

定义$ H^m(\Omega) := \{v\in L^2(\Omega): D^\xi v \in L^2(\Omega), |\xi|\leq m\} $空间的范数

$ \|u\|_{H^m(\Omega)}:= \bigg (\sum\limits_{|\xi|\leq m} \|D^\xi u \|^2\bigg )^{1/2}, $

其中$ \xi $表示非负三重指数. 使用黑体表示向量值空间, 如$ \mathit{\boldsymbol{L}}^2(\Omega) := \big(L^2(\Omega)\big)^3 $. 定义Hilbert空间

$ \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}};\Omega)=\{\mathit{\boldsymbol{Q}}\in\mathit{\boldsymbol{L}}^2(\Omega): \nabla \times\mathit{\boldsymbol{Q}}\in\mathit{\boldsymbol{L}}^2(\Omega)\}, $

$ \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}};\Omega)=\{\mathit{\boldsymbol{Q}}\in\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}};\Omega): \mathit{\boldsymbol{n}} \times\mathit{\boldsymbol{Q}}|_{\partial\Omega}=0\}, $

相应的內积和范数为

$ (\mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{P}})_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}};\Omega)}: =(\mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{P}})+(\nabla \times\mathit{\boldsymbol{Q}}, \nabla \times\mathit{\boldsymbol{P}}), \; \|\mathit{\boldsymbol{Q}}\|_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}};\Omega)}: =\sqrt{(\mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{Q}})_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}};\Omega)} }. $

$ \mathit{\boldsymbol{n}} $表示$ \partial\Omega $上的单位外法线向量.

应用上述定义, (2.6)和(2.7)式的变分形式为

(3.1) $ \begin{equation} \begin{array}{ll} \big(\partial_t\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}+\mathit{\boldsymbol{H}}_s), \mathit{\boldsymbol{Q}}\big)+\big(\gamma(u)\nabla \times\mathit{\boldsymbol{H}}, \nabla \times\mathit{\boldsymbol{Q}}\big)=0, \quad \forall\mathit{\boldsymbol{Q}}\in\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) \end{array} \end{equation} $

(3.2) $ \begin{equation} \big(\partial_t u, v\big)+\big(\lambda\nabla u, \nabla v\big)=\Big({\cal R}_r\big(\gamma(u) |\nabla \times\mathit{\boldsymbol{H}}|^2\big), v\Big), \quad \forall v\in H^1(\Omega). \end{equation} $

下面, 基于向后欧拉法, 给出(3.1)–(3.2)式的时间离散格式. 设$ n $为正整数, 将时间$ [0, T] $均匀剖分成$ n $份, 时间步长$ \tau = T/n $, 则$ \{t_i = i\tau:\; i = 0, \cdots, n\} $. 对于任意函数$ z $, 有

$ z_i=z(t_i), \; \; \delta z_i=\frac{z_i-z_{i-1}}{\tau}. $

时间离散格式为: 对于$ i=1, \cdots, n $,

(3.3) $ \begin{equation} \begin{array}{ll} \big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}\big)+\big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{Q}}\big)=0, \quad \forall\mathit{\boldsymbol{Q}}\in\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega), \end{array} \end{equation} $

(3.4) $ \begin{equation} \big(\delta u_i, v\big)+\big(\lambda_i\nabla u_i, \nabla v\big)=\Big({\cal R}_r\big(\gamma(u_{i-1})|\nabla \times\mathit{\boldsymbol{h}}_i|^2\big), v\Big), \quad \forall v\in H^1(\Omega). \end{equation} $

使用单调算子引理^{[13, 18]}, 证明在每个时间步上, (3.3)式解的存在唯一性.

定理3.1  令(2.2), (2.3), (2.8)式均满足, 设$ \mathit{\boldsymbol{H}}_0\in \mathit{\boldsymbol{L}}^2(\Omega) $, $ u_0\in L^2(\Omega) $, $ \mathit{\boldsymbol{H}}_{s}\in L^2((0, T); $$ \mathit{\boldsymbol{L}}^2(\Omega)) $, 则对于任意的$ i=1, \cdots, n $, (3.3)和(3.4)式存在唯一的解$ \mathit{\boldsymbol{h}}_i\in\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $, $ u_i\in H^1(\Omega) $.

证  定义算子$ {\cal L}_{\gamma, i}:\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega)\rightarrow \mathit{\boldsymbol{H}}^{-1}(\mathit{\boldsymbol{curl}}, \Omega) $满足

$ \begin{array}{ll} \langle {\cal L}_{\gamma, i}(\mathit{\boldsymbol{h}}), \mathit{\boldsymbol{Q}}\rangle:=\Big(\frac{\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}+\mathit{\boldsymbol{H}}_{s, i})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}_{s, i})}{\tau}, \mathit{\boldsymbol{Q}}\Big) + \big(\gamma\nabla \times\mathit{\boldsymbol{h}}, \nabla \times\mathit{\boldsymbol{Q}}\big). \end{array} $

为了在时间步$ t_i $上得到唯一的解$ \mathit{\boldsymbol{h}}_i $, 需要满足

$ \begin{array}{ll} \langle {\cal L}_{\gamma(u_{i-1}), i}(\mathit{\boldsymbol{h}}_i), \mathit{\boldsymbol{Q}}\rangle=\Big(\frac{\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_{i-1}+\mathit{\boldsymbol{H}}_{s, i-1})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}_{s, i})}{\tau}, \mathit{\boldsymbol{Q}}\Big). \end{array} $

由于上式右端已知, 算子$ {\cal L}_{\gamma(u_{i-1}), i} $是半连续的, 严格单调的和强制的. 根据文献[18, 定理18.2], 能够证明(3.3)式解的存在性.

接下来给出唯一性. 设$ \mathit{\boldsymbol{h}}_1 $和$ \mathit{\boldsymbol{h}}_2 $是两个不同的解, 有

$ \begin{eqnarray*} 0 =\langle {\cal L}_{\gamma(u_{i-1}), i}(\mathit{\boldsymbol{h}}_1) - {\cal L}_{\gamma(u_{i-1}), i}(\mathit{\boldsymbol{h}}_2), \mathit{\boldsymbol{h}}_1 - \mathit{\boldsymbol{h}}_2\rangle \ge C \| \mathit{\boldsymbol{h}}_1 - \mathit{\boldsymbol{h}}_2 \|_{\mathit{\boldsymbol{H}} (\mathit{\boldsymbol{curl}}, \Omega)}. \end{eqnarray*} $

因此, 可以得到$ \mathit{\boldsymbol{h}}_1=\mathit{\boldsymbol{h}}_2 $.

显然, 由Lax-Milgram定理可知, 线性问题(3.4)具有唯一的解.

此外, 构造时间上的分片常数插值和分片线性函数插值, 对于任意的$ i=1, \cdots, n $, 函数$ f_{i} $表示为

$ \begin{array}{ll} \overline{f}_n(0)=f_n(0)=f_0, &\\ \overline{f}_n(t)=f_i, \; \; {f}_n(t)=f_{i-1}+(t-t_{i-1})\delta f_i \; \; t\in(t_{i-1}, t_i]. \end{array} $

在文献[16]中证明了下述定理, 该定理给出了时间离散格式(3.3)–(3.4)解$ (\mathit{\boldsymbol{h}}_i, u_i) $的收敛结果, 证明了(3.1)–(3.2)式弱解的存在性.

定理3.2  令(2.2)–(2.5), (2.8)式均满足, 设$ u_0\in H^1(\Omega) $, $ \mathit{\boldsymbol{H}}_{s}\in H^1((0, T);\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)) $, $ \gamma(s) $是全局Lipschitz连续函数, 使得

$ \begin{array}{ll} {\rm (i)}\hskip 0.5cm& \mbox{在}\; C([0, T];L^2(\Omega))\; \mbox{中}\; \; u_n\rightarrow u, \; \; \overline{u}_n\rightarrow u, \\ \hskip 1cm &\mbox{在}\; H^1(\Omega)\; \mbox{中}\; \; \overline{u}_n(t)\rightharpoonup u(t), \; \; \forall t\in [0, T], \\ {\rm (ii)}\hskip 0.5cm& \mbox{在}\; L^2((0, T);L^2(\Omega)) \; \mbox{中}\; \; \overline{\gamma}_n\rightarrow \gamma(u), \; \; \overline{\gamma}_n(t-\tau)\rightarrow \gamma(u), \\ {\rm (iii)}\hskip 0.5cm& \mbox{在}\, L^2((0, T);\mathit{\boldsymbol{H}}^{-1}(\mathit{\boldsymbol{curl}}, \Omega)) \; \mbox{中}\; \; \overline{\mathit{\boldsymbol{B}}}_n-\mathit{\boldsymbol{B}}_n\rightarrow {\bf{0}}, \\ {\rm (iv)} \hskip 0.5cm& \mbox{在}\, L^2((0, T);\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)) \; \mbox{中}\; \; \mathit{\boldsymbol{H}}_{s, n}\rightarrow \mathit{\boldsymbol{H}}_s, \\ {\rm (v)}\hskip 0.5cm &\mbox{在}\, L^2((0, T);\mathit{\boldsymbol{L}}^2(\Omega)) \; \mbox{中}\; \; \overline{\mathit{\boldsymbol{h}}}_n\rightarrow \mathit{\boldsymbol{H}}, \; \; \mathit{\boldsymbol{B}}_n\rightharpoonup\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}+\mathit{\boldsymbol{H}}_{s}), \\ {\rm (vi)} \hskip 0.5cm &\mbox{在}\, L^2((0, T);\mathit{\boldsymbol{H}}^{-1}(\mathit{\boldsymbol{curl}}, \Omega))\; \mbox{中}\; \; \partial_t\mathit{\boldsymbol{B}}_n\rightharpoonup\partial_t\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{H}}+\mathit{\boldsymbol{H}}_{s}) , \\ {\rm (vii)} \hskip 0.5cm& \mathit{\boldsymbol{H}}\; \mbox{和}\; u\; \mbox{求解}\; (3.1), \\ {\rm (viii)} \hskip 0.5cm & \mbox{在}\, L^2((0, T);\mathit{\boldsymbol{L}}^2(\Omega)) \; \mbox{中}\; \; \nabla \times\overline{\mathit{\boldsymbol{h}}}_n\rightarrow \nabla \times\mathit{\boldsymbol{H}}, \\ {\rm (ix)} \hskip 0.5cm& \mathit{\boldsymbol{H}}\; \mbox{和}\; u\; \mbox{求解}\; (3.2). \end{array} $

本节将给出(3.1)–(3.2)式的全离散有限元格式. 设$ {\cal T}^h $是$ \Omega $上的正则的四面体三角剖分, 网格尺寸为$ h $. 引入Nédélec $ \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega) $—协调有限元空间^[14], 定义如下

$ \mathit{\boldsymbol{V}}_h=\{\mathit{\boldsymbol{v}}^h\in\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega), \; \mbox{在}\; K\; \mbox{上}\; \mathit{\boldsymbol{v}}^h=\mathit{\boldsymbol{a}}_K+\mathit{\boldsymbol{b}}_K\times\mathit{\boldsymbol{x}}, \forall K\in {\cal T}^h\}, $

其中$ \mathit{\boldsymbol{a}}_K $和$ \mathit{\boldsymbol{b}}_K $为常数向量. 已知任意函数$ \mathit{\boldsymbol{v}}^h\in \mathit{\boldsymbol{V}}_h $都是由每个元素$ K\in {\cal T}^h $的集合$ M_E(\mathit{\boldsymbol{v}}) $中的自由度唯一确定的

$ M_E(\mathit{\boldsymbol{v}})=\Big\{\int_{e} \mathit{\boldsymbol{v}}\cdot \tau ds; e\; \mbox{是}\; K\; \mbox{的边缘}\Big\}, $

其中$ \tau $是边缘上的单位切向量. 定义有限元空间

$ W_h=\{w^h\in H^1(\Omega) \cap C(\overline{\Omega}), w^h|_{\cal K}\in P_1({\cal K}), {\cal K}\in{\cal T} \}, $

$ \mathit{\boldsymbol{V}}_h^0=\{\mathit{\boldsymbol{v}}^h\in\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega)\cap\mathit{\boldsymbol{V}}_h\}, $

其中$ P_1(K) $是线性多项式空间. 令$ \mathit{\boldsymbol{\pi}}^h:\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)\rightarrow \mathit{\boldsymbol{V}}_h $是投影算子, 定义为

(4.1) $ \begin{equation} (\nabla \times\mathit{\boldsymbol{\pi}}^h \mathit{\boldsymbol{U}}, \nabla\times\mathit{\boldsymbol{Q}}^h)+(\mathit{\boldsymbol{\pi}}^h \mathit{\boldsymbol{U}}, \mathit{\boldsymbol{Q}}^h)=(\nabla \times \mathit{\boldsymbol{U}}, \nabla\times\mathit{\boldsymbol{Q}}^h)+(\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{Q}}^h)\; \; \forall \mathit{\boldsymbol{Q}}^h\in \mathit{\boldsymbol{V}}_h, \end{equation} $

令$ \Pi^h:H^1(\Omega)\rightarrow W_h $是Galerkin投影算子, 有

(4.2) $ \begin{equation} (\nabla \Pi^h u, \nabla v^h)+( \Pi^h u, v^h) =(\nabla u, \nabla v^h)+(u, v^h)\; \; \forall v^h\in W_h. \end{equation} $

全离散有限元格式如下: 给定$ \mathit{\boldsymbol{h}}_0^h=\mathit{\boldsymbol{\pi}}^h \mathit{\boldsymbol{H}}_0 $和$ u_0^h=\Pi^h u_0 $, 对于任意的$ i=1, \cdots, n $, 求解$ \mathit{\boldsymbol{h}}_i^h\in \mathit{\boldsymbol{V}}_h^0 $和$ u_i^h\in W_h $, 使得

(4.3) $ \begin{equation} \big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}^h\big)+\big(\gamma(u_{i-1}^h)\nabla \times\mathit{\boldsymbol{h}}_i^h, \nabla \times\mathit{\boldsymbol{Q}}^h\big)=0, \quad \forall \mathit{\boldsymbol{Q}}^h\in \mathit{\boldsymbol{V}}_h^0, \end{equation} $

(4.4) $ \begin{equation} \big(\delta u_i^h, v^h\big)+\big(\lambda_i\nabla u_i^h, \nabla v^h\big)=\Big({\cal R}_r\big(\gamma(u_{i-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_i^h|^2\big), v^h\Big), \quad \forall v^h\in W_h. \end{equation} $

在下面的定理中, 将证明离散问题(4.3)的可解性. 使用Lax-Milgram定理, 容易得到(4.4)式解是存在唯一的.

定理4.1  令定理3.1的假设条件均满足. 对$ \forall i=1, \cdots, n $, 全离散格式(4.3)存在唯一的解$ \mathit{\boldsymbol{h}}_i^h\in \mathit{\boldsymbol{V}}_h^0 $.

证  在每个时间步上需要求解$ \mathit{\boldsymbol{h}}^h\in \mathit{\boldsymbol{V}}_h^0 $

(4.5) $ \begin{equation} \begin{array}{ll} \frac{1}{\tau}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s}), \mathit{\boldsymbol{Q}}^h\big)+\big(\gamma\nabla\times \mathit{\boldsymbol{h}}^h, \nabla\times\mathit{\boldsymbol{Q}}^h\big)=\big(\mathit{\boldsymbol{f}}, \mathit{\boldsymbol{Q}}^h\big), \end{array} \end{equation} $

$ \forall\mathit{\boldsymbol{Q}}^h\in \mathit{\boldsymbol{V}}_h^0 $, 这里$ \mathit{\boldsymbol{f}} $是已知函数. 基函数表示为$ \mathit{\boldsymbol{\varphi}}_i $, 则$ \mathit{\boldsymbol{V}}_h^0=span\{\mathit{\boldsymbol{\varphi}}_1, \mathit{\boldsymbol{\varphi}}_2, \dots, \mathit{\boldsymbol{\varphi}}_k\} $, $ k $是网格边数. 记$ \mathit{\boldsymbol{h}}^h = \sum\limits_{i=1}^{k} \alpha_i\mathit{\boldsymbol{\varphi}}_i $, 其中$ \mathit{\boldsymbol{\alpha}} = \big(\alpha_1, \alpha_2, \dots, \alpha_k\big) $. 定义非线性算子$ {\cal L} $是$ {\Bbb R}^k $到$ {\Bbb R}^k $的映射: $ {\cal L}(\mathit{\boldsymbol{\alpha}})=\big({\cal L}_1(\mathit{\boldsymbol{\alpha}}), \dots, {\cal L}_{k}(\mathit{\boldsymbol{\alpha}})\big) $,

$ \begin{eqnarray*} {\cal L}_j(\mathit{\boldsymbol{\alpha}}) =\frac{1}{\tau}\Big(\mathit{\boldsymbol{B}}\big(\sum\limits_{i=1}^{k}\alpha_i\mathit{\boldsymbol{\alpha}}_i +\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s}\big)-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s}), \mathit{\boldsymbol{\alpha}}_j\Big) +\Big(\gamma\nabla\times\sum\limits_{i=1}^{k}\alpha_i\mathit{\boldsymbol{\alpha}}_i, \nabla\times\mathit{\boldsymbol{\alpha}}_i\Big) -\big(\mathit{\boldsymbol{f}}, \mathit{\boldsymbol{\alpha}}_j\big), \end{eqnarray*} $

其中$ j=1, \dots, k $. 这样问题就简化成对非线性代数方程$ \mathit{\boldsymbol{L}}(\mathit{\boldsymbol{\alpha}})={\bf{0}} $的求解. 对于算子$ \mathit{\boldsymbol{L}} $, 有

$ \begin{eqnarray*} \mathit{\boldsymbol{L}}(\mathit{\boldsymbol{\alpha}}) \cdot \mathit{\boldsymbol{\alpha}} &\ge&\frac{b_*}{\tau}\Big\|\sum\limits_{i=1}^{k}\alpha_i\mathit{\boldsymbol{\alpha}}_i\Big\|^2 +\gamma_*\Big\|\sum\limits_{i=1}^{k}\alpha_i\nabla\times\mathit{\boldsymbol{\alpha}}_i\Big\|^2 -\Big(\mathit{\boldsymbol{f}}, \sum\limits_{i=1}^{k}\alpha_i\mathit{\boldsymbol{\alpha}}_i\Big)\\ & \ge& C_1\Big\|\sum\limits_{i=1}^{k}\alpha_i\mathit{\boldsymbol{\alpha}}_i\Big\|^2 +\gamma_*\Big\|\sum\limits_{i=1}^{k}\alpha_i\nabla\times\mathit{\boldsymbol{\alpha}}_i\Big\|^2 -C_2\|\mathit{\boldsymbol{f}}\|^2 \\ &\ge& C\Big(|\alpha|^2 -\|\mathit{\boldsymbol{f}}\|^2\Big). \end{eqnarray*} $

根据文献[18, 引理18.2], 我们得出结论, 在集合$ \{\mathit{\boldsymbol{\alpha}}\in {\Bbb R}^k:\; |\mathit{\boldsymbol{\alpha}}| \le r\} $中, 如果$ r > \|\mathit{\boldsymbol{f}}\| $, 则方程$ \mathit{\boldsymbol{L}}(\mathit{\boldsymbol{\alpha}})={\bf{0}} $至少有一个解.

下面, 讨论(4.5)式解的唯一性. 设$ \mathit{\boldsymbol{h}}^h_1 $和$ \mathit{\boldsymbol{h}}^h_2 $是两个不同的解, 有

$ \begin{eqnarray*} 0 =\frac{1}{\tau}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}^h_1+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}^h_2+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s}), \mathit{\boldsymbol{Q}}^h\big)+\big(\gamma\nabla\times (\mathit{\boldsymbol{h}}^h_1-\mathit{\boldsymbol{h}}^h_2), \nabla\times\mathit{\boldsymbol{Q}}^h\big). \end{eqnarray*} $

取$ \mathit{\boldsymbol{Q}}^h=\mathit{\boldsymbol{h}}^h_1-\mathit{\boldsymbol{h}}^h_2 $, 有

$ \begin{eqnarray*} 0 \geq \frac{b_*}{\tau}\big\|\mathit{\boldsymbol{h}}^h_1-\mathit{\boldsymbol{h}}^h_2\big\|^2+ \gamma_*\big\|\nabla \times(\mathit{\boldsymbol{h}}^h_1-\mathit{\boldsymbol{h}}^h_2)\big\|^2 \geq C \big\|\mathit{\boldsymbol{h}}^h_1-\mathit{\boldsymbol{h}}^h_2\big\|^2_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)} \end{eqnarray*} $

因此, 可以得到$ \mathit{\boldsymbol{h}}^h_1=\mathit{\boldsymbol{h}}^h_2 $.

下面的两个引理将给出$ (\mathit{\boldsymbol{h}}_i^h, u_i^h) $的稳定性估计.

引理4.1  假设$ u_0\in H^1(\Omega) $, 则存在一个正的常数$ C_r $, 取决于截断函数$ R_r $中的参数$ r $, 使得

$ \begin{array}{ll} {\rm (i)}\hskip 0.5cm &{ } \sum\limits_{i=1}^{n}\|\delta u_i^h\|^2\tau+\max\limits_{1\leq j\leq n}\|\nabla u_j^h\|^2+\sum\limits_{i=1}^{n}\|\nabla u_i^h-\nabla u_{i-1}^h\|^2\leq C_r, \\ {\rm (ii)}\hskip 0.5cm &{ } \max\limits_{1\leq j\leq n}\|u_j^h\|^2\leq C_r, \\ {\rm (iii)} \hskip 0.5cm & \big(\delta u_j^h, v^h\big) \leq C_r \|v^h\|_{H^1(\Omega)}\; \; 1\leq j\leq n, \; \; \forall v^h\in W_h. \end{array} $

证  (ⅰ) 在(4.4)中取$ v^h=\delta u_i^h\tau $, 对$ i=1, \cdots, j $$ (1\leq j\leq n ) $求和,

(4.6) $ \begin{equation} \sum\limits_{i=1}^{j}\big\|\delta u_i^h\big\|^2\tau+\sum\limits_{i=1}^{j}\big(\lambda_i\nabla u_i^h, \nabla u_i^h-\nabla u_{i-1}^h\big) =\sum\limits_{i=1}^{j}\Big({\cal R}_r\big(\gamma(u_{i-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_i^h|^2\big), \delta u_i^h\Big)\tau. \end{equation} $

对(4.6)式左端第二项处理(参考文献[6, 引理5, (ⅰ)]), 有

$ \begin{eqnarray*} \sum\limits_{i=1}^{j}\big(\lambda_i\nabla u_i^h, \nabla u_i^h-\nabla u_{i-1}^h\big)&=&\frac{1}{2}\int_\Omega\lambda_{j}|\nabla u_j^h|^2 {\rm d}\mathit{\boldsymbol{x}}+\frac{1}{2}\sum\limits_{i=1}^{j}\int_\Omega\lambda_i |\nabla u_i^h-\nabla u_{i-1}^h|^2 {\rm d}\mathit{\boldsymbol{x}}\\ &&-\frac{1}{2}\int_\Omega\lambda_{1}|\nabla u_0^h|^2 {\rm d}\mathit{\boldsymbol{x}}-\frac{1}{2}\sum\limits_{i=1}^{j}\int_\Omega(\lambda_{i+1}-\lambda_i) |\nabla u_i^h|^2 {\rm d}\mathit{\boldsymbol{x}}\\ &\geq&\frac{\lambda_*}{2}\|\nabla u_j^h\|^2 +\frac{\lambda_*}{2}\sum\limits_{i=1}^{j}\|\nabla u_i^h-\nabla u_{i-1}^h\|^2 \\ & &-\frac{\lambda^*}{2}\|\nabla u_0^h\|^2 -\frac{C_\lambda}{2}\sum\limits_{i=1}^{j}\|\nabla u_i^h\|^2 \tau. \end{eqnarray*} $

由于$ {\cal R}_r $是有界函数, 因此使用Hlöder不等式和Young不等式, 有

$ \begin{eqnarray*} \sum\limits_{i=1}^{j}\Big({\cal R}_r\big(\gamma(u_{i-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_i^h|^2\big), \delta u_i^h\Big)\tau &\leq& \sum\limits_{i=1}^{j} \big\| {\cal R}_r\big(\gamma(u_{i-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_i^h|^2\big) \big\| \big\| \delta u_i^h \big\| \tau \\ &\leq &\sum\limits_{i=1}^{j} C(r) \| \delta u_i^h \| \tau \\ & \leq& C_r+\varepsilon\sum\limits_{i=1}^{j}\|\delta u_i^h\|^2\tau . \end{eqnarray*} $

整理上述估计, 应用Gronwall不等式, 能够得到(ⅰ).

(ⅱ) 由上述(ⅰ)和$ u_j^h=u_0^h+ \sum\limits_{i=1}^{j}\delta u_i^h\tau $, 易得

$ \|u_j^h\|^2\leq \|u_0^h\|^2+C\sum\limits_{i=1}^{j}\|\delta u_i^h\|^2\tau\leq C_r. $

(ⅲ) 对于任意的$ v^h\in W_h $, 有

$ \begin{eqnarray*} \big(\delta u_j^h, v^h\big) &=&-\big(\lambda_j\nabla u_j^h, \nabla v^h\big)+\Big({\cal R}_r\big(\gamma(u_{j-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_j^h|^2\big), v^h\Big)\\ &\leq& C \|\nabla u_j^h\|\cdot\|\nabla v^h\|+C_r\|v^h\|\leq C_r \|v^h\|_{H^1(\Omega)}. \end{eqnarray*} $

证毕.

类似于引理4.1中(ⅲ)的证明, 在时间离散格式(3.4)中, 能够推导出

$ \big(\delta u_j, v\big)\leq C_r \|v\|_{H^1(\Omega)}\; \; \forall v\in H^1(\Omega), \; \; 1\leq j\leq n, $

得到

$ \|\delta u_j\|_{H^{-1}(\Omega)}\leq C_r. $

假设函数$ \sigma $满足

$ |\sigma(v_1)-\sigma(v_2)|\leq C\|v_1-v_2\|_{H^{-1}(\Omega)}\; \; \forall v_1, v_2\in H^{1}(\Omega). $

因此

$ |\gamma(u_j)-\gamma(u_{j-1})|\leq|\sigma(u_j)-\sigma(u_{j-1})|/\sigma_{*}^{2}\leq C\|u_j-u_{j-1}\|_{H^{-1}(\Omega)}\leq C\tau. $

于是

$ |\gamma(u_j)-\gamma(u_{j-1})|\leq C\|u_j-u_{j-1}\|_{H^{-1}(\Omega)}\leq C\tau. $

这里需要注意的是, 对偶空间中的估计对于离散场是无效的, 因为变分形式的试探函数仅在$ H^1(\Omega) $的子空间$ W_h $中, 现在假设

$ \begin{array}{ll} \frac{\big|\big(v^h_1-v^h_2, v^h\big)\big|}{\big\|v^h\big\|_{H^1(\Omega)}} \leq C\; \; \; \; \forall\; 0\neq v^h\in W_h, \end{array} $

有

(4.7) $ \begin{equation} \begin{array}{ll} |\gamma(v^h_1)-\gamma(v^h_2)|\leq C\frac{\big|\big(v^h_1-v^h_2, v^h\big)\big|}{\big\|v^h\big\|_{H^1(\Omega)}}, \, \forall v^h_1, v^h_2\in W_h. \end{array} \end{equation} $

使用引理4.1 (ⅲ) 得到

$ |\gamma(u_j^h)-\gamma(u_{j-1}^h)|\leq C\tau. $

引理4.2  令(2.2)–(2.4)及(4.7)式的假设均满足, 设$ \mathit{\boldsymbol{H}}_{s}\in H^1((0, T);\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)) $, 则存在一个正的常数$ C $, 使得

$ \begin{array}{ll} {\rm(i)}\hskip 0.5cm &{ } \sum\limits_{i=1}^{j} \|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\|^2\tau +\max\limits_{1\leq j\leq n}\|\nabla \times\mathit{\boldsymbol{h}}_j^h\|^2\leq C, \\ {\rm (ii)} \hskip 0.5cm &{ } \max\limits_{1\leq j\leq n}\|\mathit{\boldsymbol{h}}^h_j+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, j}\|^2+\sum\limits_{i=1}^{n}\|\nabla \times\mathit{\boldsymbol{h}}_i^h\|^2\tau\leq C. \end{array} $

证  (ⅰ) 在(4.3)式中取$ \mathit{\boldsymbol{Q}}^h=\tau\delta\mathit{\boldsymbol{h}}_i^h $, 对$ i=1, \dots, j $求和,

$ \begin{eqnarray*} & &\sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \delta\mathit{\boldsymbol{h}}_i^h +\mathit{\boldsymbol{\pi}}^h\delta\mathit{\boldsymbol{H}}_{s, i}\big)\tau + \sum\limits_{i=1}^{j}\big(\gamma(u_{i-1}^h)\nabla \times\mathit{\boldsymbol{h}}_i^h, \nabla \times\delta\mathit{\boldsymbol{h}}_i^h\big)\tau\\ &=&\sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{\pi}}^h\delta\mathit{\boldsymbol{H}}_{s, i}\big)\tau. \end{eqnarray*} $

结合(2.3)式, 对上式左端第一项估计,

$ \sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\big)\tau \geq b_* \sum\limits_{i=1}^{j} \|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\|^2\tau. $

对左端第二项估计, 由引理4.1中的(ⅲ)和(4.7)式, 易得

$ \begin{eqnarray*} & & \sum\limits_{i=1}^{j}\big(\gamma(u_{i-1}^h)\nabla \times\mathit{\boldsymbol{h}}_i^h, \delta\nabla \times\mathit{\boldsymbol{h}}_i^h\big)\tau\\ &= &\frac{1}{2}\int_{\Omega} \gamma(u_{j}^h)|\nabla \times\mathit{\boldsymbol{h}}_j^h|^2 {\rm d}\mathit{\boldsymbol{x}}+ \frac{1}{2} \sum\limits_{i=1}^{j}\int_{\Omega} \gamma(u_{i-1}^h)|\nabla \times\mathit{\boldsymbol{h}}_i^h-\nabla \times\mathit{\boldsymbol{h}}_{i-1}^h|^2 {\rm d}\mathit{\boldsymbol{x}}\\ &&- \frac{1}{2}\int_{\Omega} \gamma(u_0^h)|\nabla \times\mathit{\boldsymbol{h}}_0^h|^2 {\rm d}\mathit{\boldsymbol{x}}- \frac{1}{2} \sum\limits_{i=1}^{j}\int_\Omega (\gamma(u_{i}^h)-\gamma(u_{i-1}^h))|\nabla \times\mathit{\boldsymbol{h}}_i^h|^2 {\rm d}\mathit{\boldsymbol{x}}\\ &\geq & \frac{\gamma_*}{2}\|\nabla \times\mathit{\boldsymbol{h}}_j^h\|^2+ \frac{\gamma_*}{2} \sum\limits_{i=1}^{j}\|\nabla \times\mathit{\boldsymbol{h}}_i^h\\ & &-\nabla \times\mathit{\boldsymbol{h}}_{i-1}^h\|^2- \frac{\gamma^*}{2}\|\nabla \times\mathit{\boldsymbol{h}}_0^h\|^2- C \sum\limits_{i=1}^{j}\|\nabla \times\mathit{\boldsymbol{h}}_i^h\|^2\tau. \end{eqnarray*} $

利用矢量场$ \mathit{\boldsymbol{B}} $的Lipschitz连续性及$ \mathit{\boldsymbol{H}}_{s}\in H^1((0, T);\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)) $, 对右端处理, 得到

$ \sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{\pi}}^h\delta\mathit{\boldsymbol{H}}_{s, i}\big) \tau\leq \varepsilon\sum\limits_{i=1}^{j}\big\|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\big\|^2\tau+C. $

整理上述估计, 应用Gronwall不等式, 得到

$ \sum\limits_{i=1}^{j} \|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\|^2 +\|\nabla \times\mathit{\boldsymbol{h}}_j^h\|^2\leq C. $

(ⅱ) 在(4.3)式中取$ \mathit{\boldsymbol{Q}}^h=\tau\mathit{\boldsymbol{h}}_i^h $, 对$ i=1, \dots, j $$ (1\leq j\leq n ) $求和,

$ \begin{eqnarray*} &&\sum\limits_{i=1}^{j}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_{i-1}^h +\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i-1}), \mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}\big)\\ & &+ \sum\limits_{i=1}^{j}\big(\gamma(u_{i-1}^h)\nabla \times\mathit{\boldsymbol{h}}_i^h, \nabla \times\mathit{\boldsymbol{h}}_i^h\big)\tau\\ &=&\sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}\big)\tau. \end{eqnarray*} $

对于上式左端第一项, 由(2.3)和(2.4)式可以得到

$ \begin{eqnarray*} & &\sum\limits_{i=1}^{j}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}) -\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_{i-1}^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i-1}), \mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}\big)\\ &=&\sum\limits_{i=1}^{j}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})- \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_{i-1}^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i-1}), \mathit{\boldsymbol{B}}^{-1}(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}))\big)\\ &\geq& \sum\limits_{i=1}^{j}\int_{\Omega}\Big[\Phi_{\mathit{\boldsymbol{B}}^{-1}}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\big) -\Phi_{\mathit{\boldsymbol{B}}^{-1}}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_{i-1}^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i-1})\big)\Big] {\rm d}\mathit{\boldsymbol{x}}\\ &=&\int_{\Omega}\Big[\Phi_{\mathit{\boldsymbol{B}}^{-1}}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_j^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, j})\big) -\Phi_{\mathit{\boldsymbol{B}}^{-1}}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_0^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, 0})\big)\Big] {\rm d}\mathit{\boldsymbol{x}}\\ &\geq &C_0 \|\mathit{\boldsymbol{h}}_j^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, j}\|^2-C. \end{eqnarray*} $

对于左端第二项, 有

$ \sum\limits_{i=1}^{j}\big(\gamma(u_{i-1}^h)\nabla \times\mathit{\boldsymbol{h}}_i^h, \nabla \times\mathit{\boldsymbol{h}}_i^h\big)\tau\geq \gamma_*\sum\limits_{i=1}^{j}\|\nabla \times\mathit{\boldsymbol{h}}_i^h\|^2\tau. $

使用Cauchy不等式, 结合假设条件$ \mathit{\boldsymbol{H}}_{s}\in H^1((0, T);\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)) $及矢量场$ \mathit{\boldsymbol{B}} $的Lipschitz连续性, 得到

$ \begin{eqnarray*} \sum\limits_{i=1}^{j}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i}\big)\tau &\leq& C\sum\limits_{i=1}^{j} \|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\|\cdot\|\mathit{\boldsymbol{H}}_{s, i}\|_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)}\tau\\ &\leq &C+C\sum\limits_{i=1}^{j}\|\delta(\mathit{\boldsymbol{h}}_i^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, i})\|^2\tau\leq C. \end{eqnarray*} $

因此, 有

$ \|\mathit{\boldsymbol{h}}_j^h+\mathit{\boldsymbol{\pi}}^h\mathit{\boldsymbol{H}}_{s, j}\|^2+\sum\limits_{i=1}^{j}\|\nabla \times\mathit{\boldsymbol{h}}_i^h\|^2\tau\leq C. $

证毕.

本节的目的是证明当$ \tau, h\rightarrow 0 $时全离散格式解的收敛性. 首先确定时间步长$ \tau $, 令网格尺寸$ h $趋向于零. 这样得到时间离散格式(3.3)–(3.4)式的解$ (\mathit{\boldsymbol{h}}_i, u_i) $. 具体过程见定理5.1和5.2. 第二步, 令$ \tau\rightarrow 0 $, 证明问题(3.3)–(3.4)的解$ (\mathit{\boldsymbol{h}}_i, u_i) $收敛于(3.1)–(3.2)式的弱解$ (\mathit{\boldsymbol{H}}, u) $. 收敛结果已在定理3.2完成.

不失一般性, 设$ {\cal T}_1\prec {\cal T}_2\prec \cdots {\cal T}_k\prec \cdots $是$ \Omega $中均匀且形状规则的网格序列, 使得$ \lim\limits_{k\rightarrow \infty} h_k =0 $, $ {\cal T}_{k+1} $表示网格$ {\cal T}_k $的加密. 为了明确离散解对$ {\cal T}_k $的依赖程度, 对离散解标注一个上标, 记为$ \mathit{\boldsymbol{h}}_i^{(k)} :=\mathit{\boldsymbol{h}}_i^h, $$ u_i^{(k)} :=u_i^h. $ 定义空间$ \mathit{\boldsymbol{V}}_h $, $ \mathit{\boldsymbol{V}}_h^0 $和$ W_h $, 这取决于网格划分$ {\cal T}_k $, 分别为$ \mathit{\boldsymbol{V}}_h^k $, $ \mathit{\boldsymbol{V}}_h^{0, k} $和$ W_h^k $. (4.1)和(4.2)分别定义了投影算子$ \mathit{\boldsymbol{\pi}}^k:\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)\rightarrow \mathit{\boldsymbol{V}}_h^k $和$ \Pi^k:H^1(\Omega)\rightarrow W_h^k $. 使用这些符号, 全离散问题(4.3)–(4.4)的格式如下

(5.1) $ \begin{equation} \big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}^{(k)}\big)+ \big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{Q}}^{(k)}\big)=0, \end{equation} $

(5.2) $ \begin{equation} \big(\delta u_i^{(k)}, v^{(k)}\big)+\big(\lambda_i\nabla u_i^{(k)}, \nabla v^{(k)}\big)=\Big({\cal R}_r\big(\gamma(u_{i-1}^{(k)})|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}|^2\big), v^{(k)}\Big), \end{equation} $

其中, $ \forall\mathit{\boldsymbol{Q}}^{(k)}\in \mathit{\boldsymbol{V}}_h^{0, k} $, $ \forall v^{(k)}\in W_h^k $.

利用非线性矢量场$ \mathit{\boldsymbol{B}} $的单调性和Minty-Browder方法^{[8, 18]}克服非线性项收敛的困难, 可以证明定理5.1. 下面部分中的序列仍然是子序列, 使用相同的符号表示.

定理5.1  令引理4.1–4.2的假设均满足. 设$ \gamma(s) $是全局Lipschitz连续函数, 对于$ 1\leq i\leq n $, 当$ k\rightarrow \infty $时, 有

$ \begin{array}{ll} {\rm(i)}& \mbox{在}\; H^1(\Omega)\; \mbox{中}\; u_i^{(k)}\rightharpoonup u_i, \ \mbox{在}\; L^2(\Omega)\; \mbox{中}\; u_i^{(k)}\rightarrow u_i, \mbox{ 且 }\ \gamma\big(u_i^{(k)}\big)\rightarrow \gamma\big(u_i\big)\ \mbox{ a.e.}\ \mbox{ 在}\ \Omega \ \mbox{中}, \\ {\rm(ii)} &\mbox{在}\; \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)\; \mbox{中}\; \mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}\rightarrow \mathit{\boldsymbol{H}}_{s, i}, \\ {\rm (iii)}\ & \mbox{在}\; \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega)\; \mbox{中}\; \mathit{\boldsymbol{h}}^{(k)}_i\rightharpoonup \mathit{\boldsymbol{h}}_i, \; \mbox{在}\; \mathit{\boldsymbol{L}}^2(\Omega)\; \mbox{中}\; \mathit{\boldsymbol{h}}^{(k)}_i\rightarrow \mathit{\boldsymbol{h}}_i\; \mbox{在}\; \mathit{\boldsymbol{L}}^2(\Omega), \\ {\rm (iv)}& \mbox{在}\; \mathit{\boldsymbol{L}}^2(\Omega)\; \mbox{中}\; \; \mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\rightharpoonup\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \\ {\rm (v)}& \mbox{在}\; \mathit{\boldsymbol{L}}^2(\Omega)\; \mbox{中}\; \nabla \times\mathit{\boldsymbol{h}}_i^{(k)}\rightarrow \nabla \times\mathit{\boldsymbol{h}}_i. \end{array} $

证  (ⅰ) 由引理4.1可知

$ \|u_i^{(k)}\|_{H^1(\Omega)}\leq C. $

因此, 根据$ H^1 (\Omega) $的自反性和Sobolev空间的紧嵌入, 存在一个子列和$ u_i \in H^1(\Omega) $, 使得

$ \mbox{在}\; H^1(\Omega)\; \mbox{中}\; u_i^{(k)}\rightharpoonup u_i, \quad \mbox{在}\; L^2(\Omega)\; \mbox{中}\; u_i^{(k)}\rightarrow u_i. $

利用函数$ \gamma $的Lipschitz连续性, 得到

$ \lim\limits_{n\rightarrow \infty}\|\gamma\big(u_i^{(k)}\big)-\gamma\big(u_i\big)\|^2\leq C \lim\limits_{n\rightarrow \infty}\|u_i^{(k)}-u_i\|^2 =0. $

所以$ \gamma\big(u_i^{(k)}\big)\rightarrow \gamma\big(u_i\big) $ a.e. 在$ \Omega $中.

(ⅱ) 根据投影算子(4.1)的定义, 有

$ \lim\limits_{k\rightarrow \infty} \|\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}-\mathit{\boldsymbol{H}}_{s, i}\|_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)}=0. $

(ⅲ) 利用引理4.2得到

$ \|\mathit{\boldsymbol{h}}^{(k)}_i\|^2_{\mathit{\boldsymbol{H}}(\mathit{\boldsymbol{curl}}, \Omega)}\leq C. $

因此, 可以得到一个子列$ \{\mathit{\boldsymbol{h}}^{(k)}_i\}_{k=1}^\infty $, 其弱收敛于某个$ \mathit{\boldsymbol{h}}_i\in\mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $. 利用$ \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $到$ \mathit{\boldsymbol{L}}^2(\Omega) $的紧单射, 以及$ \mathit{\boldsymbol{L}}^2(\Omega) $的紧性, 能够找到一个子列(参考文献[12]), 使得

$ \lim\limits_{k\rightarrow \infty}\|\mathit{\boldsymbol{h}}^{(k)}_i-\mathit{\boldsymbol{h}}_i\|=0. $

(ⅳ) 利用矢量场的Lipschitz连续性和引理4.2中的稳定性估计, 得到

(5.3) $ \begin{equation} \|\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\|\leq C\|\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}\|\leq C. \end{equation} $

故存在一个子列和$ \mathit{\boldsymbol{U}} \in \mathit{\boldsymbol{L}}^2(\Omega) $, 使得$ k\rightarrow \infty $时, 有

$ \mbox{在}\; \mathit{\boldsymbol{L}}^2(\Omega)\; \mbox{中}\; \mathit{\boldsymbol{B}}^{(k)}_i:=\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\rightharpoonup\mathit{\boldsymbol{U}}. $

根据矢量场$ \mathit{\boldsymbol{B}} $的单调性, 下述不等式对于任意的$ \mathit{\boldsymbol{w}}\in L^2((0, T);\mathit{\boldsymbol{L}}^2(\Omega)) $及任意非负$ \zeta\in C^\infty_0(\Omega) $成立,

(5.4) $ \begin{equation} \big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta((\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}))\big) \geq 0. \end{equation} $

(5.4)式可以分解成四项

$ \begin{eqnarray*} &&P_1=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\big), \\ & &P_2= \big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\big), \\ & &P_3=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i})\big), \\ & &P_4=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i})\big) . \end{eqnarray*} $

$ P_1 $可以写成如下形式

$ \begin{eqnarray*} & &\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\big) -\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})\big)\\ &\leq&\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i^{(k)} +\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}-(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}))\big)\\ &&+\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})\big)\\ &\leq& C\|\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})\|\big(\|\mathit{\boldsymbol{h}}_i^{(k)}-\mathit{\boldsymbol{h}}_i\|+ \|\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}-\mathit{\boldsymbol{H}}_{s, i}\|\big)\\ &&+ C\|\zeta(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})\|\big(\|\mathit{\boldsymbol{h}}_i^{(k)}-\mathit{\boldsymbol{h}}_i\|+ \|\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}-\mathit{\boldsymbol{H}}_{s, i}\|\big)\\ & &\mathop{\longrightarrow}\limits^{k\rightarrow \infty} 0.\hskip 0.5cm (\mbox{利用 }\ \mathit{\boldsymbol{B}} \ \mbox{的连续性}) \end{eqnarray*} $

因此

$ \lim\limits_{k\rightarrow \infty} P_1=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})\big). $

对其余各项取极限$ k\rightarrow \infty $, 有

$ \begin{eqnarray*} &&\lim\limits_{n\rightarrow \infty} P_2=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})\big), \\ &&\lim\limits_{n\rightarrow \infty} P_3=\big(\mathit{\boldsymbol{U}}, \zeta(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i})\big), \\ & &\lim\limits_{n\rightarrow \infty} P_4=\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i})\big) . \end{eqnarray*} $

返回到(5.4)式, 有

$ \begin{eqnarray*} & &\lim\limits_{k\rightarrow \infty}\big(\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta((\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}))\big)\\ &=&\big(\mathit{\boldsymbol{U}}-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}), \zeta((\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i})-(\mathit{\boldsymbol{w}}+\mathit{\boldsymbol{H}}_{s, i}))\big)\geq 0. \end{eqnarray*} $

由于$ \mathit{\boldsymbol{w}} $是任意选取的, 令$ \mathit{\boldsymbol{w}}=\mathit{\boldsymbol{h}}_i+\varepsilon\mathit{\boldsymbol{h}}' $, 其中$ \varepsilon>0 $, $ \mathit{\boldsymbol{h}}'\in \mathit{\boldsymbol{L}}^2(\Omega) $, 得到

$ \big(\mathit{\boldsymbol{U}}-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\varepsilon\mathit{\boldsymbol{h}}'+\mathit{\boldsymbol{H}}_{s, i}), \zeta\mathit{\boldsymbol{h}}'\big) \leq 0. $

令$ \varepsilon $趋向于$ 0 $, 则

$ \big(\mathit{\boldsymbol{U}}-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \zeta\mathit{\boldsymbol{h}}'\big)\leq 0. $

由于$ \mathit{\boldsymbol{h}}' $的选取是任意的, 令$ \mathit{\boldsymbol{h}}'=-\mathit{\boldsymbol{h}}' $, 上面的不等式反向成立, 即

$ \big(\mathit{\boldsymbol{U}}-\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \zeta\mathit{\boldsymbol{h}}'\big)= 0 $

对于任意的$ \mathit{\boldsymbol{h}}'\in \mathit{\boldsymbol{L}}^2(\Omega) $和非负$ \zeta\in C^\infty_0(\overline{\Omega}) $成立. 因此, 得到在$ \Omega $中, 几乎处处$ \mathit{\boldsymbol{U}}=\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}) $, 即在$ \mathit{\boldsymbol{L}}^2(\Omega) $中$ \mathit{\boldsymbol{B}}_i^k\rightharpoonup\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}) $.

(ⅴ) 对于任意的$ \mathit{\boldsymbol{Q}}\in \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $, 有

$ \lim\limits_{k\rightarrow \infty} \big(\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \mathit{\boldsymbol{Q}}\big) =\lim\limits_{k\rightarrow \infty} \big(\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{Q}}\big)=\big(\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{Q}}\big)= \big(\nabla \times\mathit{\boldsymbol{h}}_i, \mathit{\boldsymbol{Q}}\big). $

显然在$ \mathit{\boldsymbol{L}}^2(\Omega) $中$ \nabla \times\mathit{\boldsymbol{h}}_i^{(k)}\rightharpoonup \nabla \times\mathit{\boldsymbol{h}}_i $.

接下来, 需要讨论如下不等式

(5.5) $ \begin{eqnarray} 0&\leq&\gamma_*\int_{\Omega}\big|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}-\nabla \times\mathit{\boldsymbol{h}}_i\big|^2{\rm d}\mathit{\boldsymbol{x}}\leq\int_{\Omega}\gamma(u_{i-1}^{(k)})\big|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}-\nabla \times\mathit{\boldsymbol{h}}_i\big|^2{\rm d}\mathit{\boldsymbol{x}}{}\\ &=&\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{h}}_i^{(k)}\big)+\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{h}}_i\big){}\\ &&-2\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{h}}_i\big). \end{eqnarray} $

根据本定理中的(ⅰ), (ⅱ), 应用Lebesgue控制定理, 有(参考文献[16, 定理1 (ⅹⅲ)])

(5.6) $ \begin{equation} \lim\limits_{k\rightarrow \infty}\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{h}}_i\big)=\big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{h}}_i\big) \end{equation} $

及

(5.7) $ \begin{equation} \lim\limits_{k\rightarrow \infty}\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{h}}_i\big)=\big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{h}}_i\big). \end{equation} $

对于固定的时间步长$ \tau $, 利用(5.1), (5.3), (2.3)和本定理中的(ii)–(iii), 得到

(5.8) $ \begin{eqnarray} &&\lim\limits_{k\rightarrow \infty}\big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{h}}_i^{(k)}\big) {}\\ &=&-\lim\limits_{k\rightarrow \infty}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{h}}_i^{(k)}\big) {}\\ &=&-\lim\limits_{k\rightarrow \infty}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{h}}_i^{(k)}-\mathit{\boldsymbol{h}}_i\big) -\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{h}}_i\big) {}\\ &&-\lim\limits_{k\rightarrow \infty}\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i})-\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{h}}_i\big) {}\\ &=&-\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{h}}_i\big)=\big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{h}}_i\big), \end{eqnarray} $

整理(5.5)–(5.8)式, 有

(5.9) $ \begin{equation} \lim\limits_{k\rightarrow \infty}\int_{\Omega}\big|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}-\nabla \times\mathit{\boldsymbol{h}}_i\big|^2{\rm d}\mathit{\boldsymbol{x}}=0, \end{equation} $

故在$ \mathit{\boldsymbol{L}}^2(\Omega) $中$ \nabla \times\mathit{\boldsymbol{h}}_i^{(k)}\rightarrow \nabla \times\mathit{\boldsymbol{h}}_i $.

下面的定理表明, 当固定时间步长$ \tau $并使网格尺寸$ h $趋于零时, 得到Maxwell方程与热传导方程耦合的时间离散模型.

定理5.2  令定理5.1的假设均满足. 对于任意的$ i=1, \cdots, n $, $ \mathit{\boldsymbol{h}}_i\in \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $和$ u_i\in H^1(\Omega) $是$ (3.3) $–$ (3.4) $式的唯一解.

证  首先证明$ (\mathit{\boldsymbol{h}}_i, u_i) $求解$ (3.3) $式. 利用(5.1)式及$ \mathit{\boldsymbol{V}}_h^{0, l}\subset\mathit{\boldsymbol{V}}_h^{0, k} $, 对于$ l\leq k $, 有

$ \begin{array}{ll} &\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i^{(k)}+\mathit{\boldsymbol{\pi}}^k\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}^{(l)}\big)+ \big(\gamma(u_{i-1}^{(k)})\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}, \nabla \times\mathit{\boldsymbol{Q}}^{(l)}\big)=0\; \; \forall \mathit{\boldsymbol{Q}}^{(l)}\in \mathit{\boldsymbol{V}}_h^{0, l}. \end{array} $

对上式取极限$ k\rightarrow \infty $, 有

$ \begin{array}{ll} &\big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}^{(l)}\big)+ \big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{Q}}^{(l)}\big)=0\; \; \forall \mathit{\boldsymbol{Q}}^{(l)}\in \mathit{\boldsymbol{V}}_h^{0, l}. \end{array} $

当$ l\rightarrow \infty $时, 由$ \mathit{\boldsymbol{V}}_h^{0, l} $在$ \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega) $的稠密性, 得到

(5.10) $ \begin{equation} \begin{array}{ll} \big(\delta\mathit{\boldsymbol{B}}(\mathit{\boldsymbol{h}}_i+\mathit{\boldsymbol{H}}_{s, i}), \mathit{\boldsymbol{Q}}\big)+ \big(\gamma(u_{i-1})\nabla \times\mathit{\boldsymbol{h}}_i, \nabla \times\mathit{\boldsymbol{Q}}\big)=0\; \; \forall \mathit{\boldsymbol{Q}}\in \mathit{\boldsymbol{H}}_0(\mathit{\boldsymbol{curl}}, \Omega). \end{array} \end{equation} $

接下来, 为了证明$ \mathit{\boldsymbol{h}}_i $和$ u_i $求解(3.4)式, 对于$ l\leq k $, 有

(5.11) $ \begin{equation} \big(\delta u_i^{(k)}, v^{(l)}\big)+\big(\lambda_i\nabla u_i^{(k)}, \nabla v^{(l)}\big)=\Big({\cal R}_r\big(\gamma(u_{i-1}^{(k)})|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}|^2\big), v^{(l)}\Big)\; \; \forall v^{(l)}\in W_h^l . \end{equation} $

利用定理5.1和Lebesgue控制收敛定理, 注意到函数$ {\cal R}_r $是连续且有界的, 得到

$ \lim\limits_{k\rightarrow \infty}\Big({\cal R}_r\big(\gamma(u_{i-1}^{(k)})|\nabla \times\mathit{\boldsymbol{h}}_i^{(k)}|^2\big), v^{(l)}\Big) =\Big({\cal R}_r\big(\gamma(u_{i-1})|\nabla \times\mathit{\boldsymbol{h}}_i|^2\big), v^{(l)}\Big). $

对(5.11)式取极限, 有

$ \big(\delta u_i, v^{(l)}\big)+\big(\lambda_i\nabla u_i, \nabla v^{(l)}\big)=\Big({\cal R}_r\big(\gamma(u_{i-1})|\nabla \times\mathit{\boldsymbol{h}}_i|^2\big), v^{(l)}\Big)\; \; \forall v^{(l)}\in W_h^l . $

当$ l\rightarrow \infty $时, 由$ W_h^l $在$ H^1(\Omega) $中的稠密性, 得到

$ \begin{eqnarray*} \big(\delta u_i, v\big)+\big(\lambda_i\nabla u_i, \nabla v\big)=\Big({\cal R}_r\big(\gamma(u_{i-1})|\nabla \times\mathit{\boldsymbol{h}}_i|^2\big), v\Big)\; \forall v\in H^1(\Omega). \end{eqnarray*} $

证毕.

本节将给出非线性感应加热问题的数值实验.

实验6.1  本次实验的目的是在固定时间步长下, 检验当网格尺寸$ h $减小时误差的变化. 计算区域$ \Omega $是一个单位立方体, 包含有限数量的标准四面体.

选取满足条件的非线性函数

$ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{B}} (\hat{ \mathit{\boldsymbol{H}}}) := \bigl( 1 + \exp(-1-|\hat{ \mathit{\boldsymbol{H}}}|) \bigr)\hat{ \mathit{\boldsymbol{H}}}, $

$ \gamma = \gamma (u) := 4 - \biggl( 1 + \frac{1}{1 + u} \biggr)^{1 + u}, $

其中磁场$ \hat{ \mathit{\boldsymbol{H}}}= \mathit{\boldsymbol{H}} + \mathit{\boldsymbol{H}}_s $. 初始值和参数为

$ \mathit{\boldsymbol{H}}_0 = {\bf{0}}, \quad u_0 = 0, \quad\lambda = 0.1, \quad \mu = 1. $

选取源场为

$ \mathit{\boldsymbol{H}}_s := \left(\begin{array}{cc} 0\\ 0\\ \sin (20 \pi t) \bigl( x^2 + y^2 \bigr) \end{array}\right). $

将时间$ [0, 1] $均分成$ 100 $份, 使用COMSOL软件中使用2阶Nédélac单元求解$ \mathit{\boldsymbol{H}} $, 使用2阶Lagrange单元求解$ u $. 在每个时间步上使用MUMPS求解器来求解整个系统. 将立方体的每条边均匀剖分成64份, 在这种情况下, 得到的解作为参考解, 分别表示为$ \mathit{\boldsymbol{H}}_{{\rm ref}} $和$ u_{{\rm ref}} $.

为了表明文中格式解的收敛性, 计算$ h = 1/2, 1/4, 1/8, 1/16, 1/32 $的数值解$ \mathit{\boldsymbol{H}}_{{\rm n}} $和$ u_{{\rm n}} $, 将数值解与$ \mathit{\boldsymbol{H}}_{{\rm ref}} $和$ u_{{\rm ref}} $进行比较. 选取$ \Omega $中的特定测量点以及特定时间$ t_i=0.01i $, 其中$ i=1, \cdots, 10 $. $ \mathit{\boldsymbol{H}}_n $与$ \mathit{\boldsymbol{H}}_{{\rm ref}} $, $ u_n $与$ u_{{\rm ref}} $之间的相对误差为

$ \vert \mathit{\boldsymbol{H}}_{{\rm ref}} \vert = \sum\limits_{p_j \in P} \sum\limits_{i = 1}^{10} \vert \mathit{\boldsymbol{H}}_{{\rm ref}} ( P_j, t_i ) \vert, \quad \vert u_{{\rm ref}} \vert = \sum\limits_{p_j \in P} \sum\limits_{i = 1}^{10} \vert u_{{\rm ref}} ( P_j, t_i ) \vert, $

$ \vert \mathit{\boldsymbol{H}}_{{\rm ref}} - \mathit{\boldsymbol{H}}_n \vert = \sum\limits_{p_j \in P} \sum\limits_{i = 1}^{10} \vert \mathit{\boldsymbol{H}}_{{\rm ref}} ( P_j, t_i ) - \mathit{\boldsymbol{H}}_n ( P_j, t_i ) \vert, $

$ \vert u_{{\rm ref}} - u_n \vert = \sum\limits_{p_j \in P} \sum\limits_{i = 1}^{10} \vert u_{{\rm ref}} ( P_j, t_i ) - u_n ( P_j, t_i ) \vert, $

$ {\rm rel} \, \mathit{\boldsymbol{H}}_n = \frac{\vert \mathit{\boldsymbol{H}}_{{\rm ref}} - \mathit{\boldsymbol{H}}_n \vert}{\vert \mathit{\boldsymbol{H}}_{{\rm ref}} \vert}, \quad {\rm rel} \, u_n = \frac{\vert u_{{\rm ref}} - u_n \vert}{\vert u_{{\rm ref}} \vert}, $

其中$ P $是特定测量点的集合. 随着网格尺寸$ h $的减小, 相对误差的变化如图 2所示. 图 2(a)中的回归线表示为$ \log_2 ( {\rm rel} \, \mathit{\boldsymbol{H}}_n ) = 1.784 \log_2 ( \tau ) + 2.391 $, 图 2(b)中的回归线表示为$ \log_2 ( {\rm rel} \, u_n ) = 2.202 \log_2 ( \tau ) -2.485 $, 故数值解收敛于参考解.

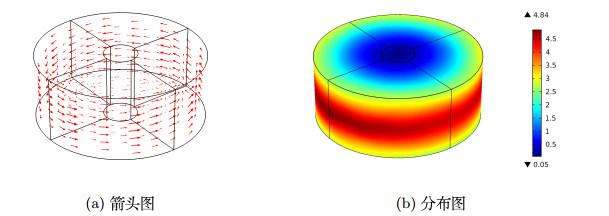
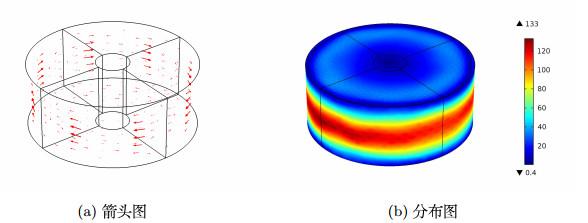
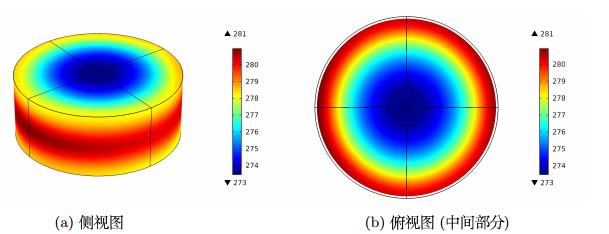
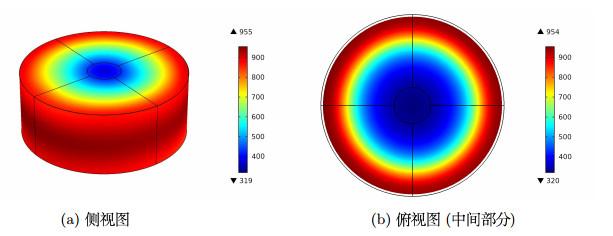
实验6.2  实验模型见图 1. 本次实验将给出一些数值模拟, 演示当改变电流频率$ \omega $时, 涡流和温度的分布情况.

交流电源为

$ \begin{eqnarray*} \mathit{\boldsymbol{J}}_s = 500 \sin (\omega t) \left(\begin{array}{cc} - y / ( x^2 + y^2 ) \\ x / ( x^2+y^2 ) \\ 0 \end{array}\right) \end{eqnarray*} $

通过线圈的交流电源产生一个通过工件的交变磁场$ \mathit{\boldsymbol{H}}_s $, 该磁场在工件中产生涡流和焦耳热. 计算区域$ \Omega $是工件. 时间为$ [0, 1] $, 时间步长$ \tau = 0.2 \pi/ \omega $.

当$ t=1.0 $时, 在不同系数$ \omega $下的涡流密度$ \nabla \times \mathit{\boldsymbol{H}} $的变化见图 3, 图 4和图 5, 温度$ u $的变化如图 6, 图 7和图 8所示.

数值模拟结果表明, 涡流的大小随着与工件表面距离的增大而减小. 当电流频率$ \omega $增加时, 涡流的分布集中在工件的外侧. 此外, 温度的分布也受$ \omega $的影响. 工件的整体温度随着$ \omega $的增加而升高, 并且工件内侧与外侧之间的温度差逐渐增大. 这表明温度的变化与涡流的分布是一致的.

本文研究了非线性Maxwell方程与热传导方程耦合的全离散有限元解耦格式. 证明了全离散格式解的存在唯一性. 同时也证明了全离散格式的解收敛于连续耦合问题的解. 通过两组数值实验来支持文中的理论结果, 实验结果表明, 理论结果与感应加热模型的实际研究结果一致.