1 引言
其中
表 1 模型(1.1)中参数的生物意义
| 参数 | 含义 |
| 人和蚊子的扩散系数( | |
| 染病者的因病死亡率 | |
| 染病蚊子的因病死亡率 | |
| 染病者的恢复率 | |
| 病毒由染病蚊子(人)到易感人(蚊子)的传播率 |
设
本文安排如下: 第二节, 给出本文主要结果; 第三节, 利用不动点定理证明辅助系统行波解的存在性; 第四节, 通过Ascoli-Arzelà引理证明系统(1.2) 行波解的存在性;第五节, 借助双边Laplace变换和反证法研究行波的不存在性; 第六节, 探讨最小波速关于模型参数的连续依赖性.
2 主要结果
若不考虑潜伏期和扩散率, 则系统(1.2)变为如下常微分系统
令
根据文献[23]知(2.1)式的基本再生数为
及边界条件
且
定理2.1 设
另外
且
定理2.2 若
定理2.3 若
注2.1 根据定理2.1–2.3可知
3 辅助系统
3.1 特征方程
将(1.2) 式在
令
系统(3.2) 可改写为
因此, 系统(2.2) 对应的特征方程为
记
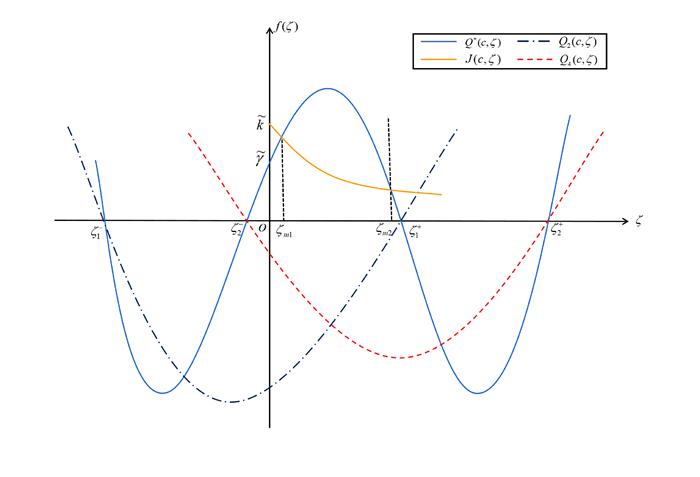
图 1
图 1
引理3.1 设
进一步, 有
其中
3.2 上下解
为研究系统(2.2) 正解的存在性, 引入辅助系统
其中
这里
设
其中
不难证明如下引理.
引理3.2 函数
注3.1 引理3.2表明
引理3.3 设
则
证 当
当
同理
注3.2 引理3.3表明
引理3.4 设
则
和
证 当
当
注3.3 引理3.4表明
引理3.5 设
和
证 引理3.5的证明类似于文献[16, 引理2.5], 不再赘述.
注3.4 因
因此,
3.3 有界正解的存在性
令
因此(3.6)式转化为
定义
和
定义算子
其中
易知, 算子
引理3.6 集合
引理3.7 算子
定义Banach空间
赋予范数
其中
引理3.8 映射
证 取
因此, 有
对于
对于
所以, 算子
引理3.9 映射
证 对
因
从而
固定整数
由Ascoli-Arzelà引理知,
则
同理,
命题3.1 设
证 结合引理3.6–3.9, 利用Schauder不动点定理知, 系统(3.6) 存在非负有界解
则
(ⅰ) 为证
因
因此,
(ⅱ) 为证
因
根据
(ⅲ) 为证(3.19)式. 因
由
(ⅳ) 最后证
显然
即
4 行波解的存在性
本节完成定理2.1的证明.
定理2.1的证明 设
取序列
因
即
因此,
下证
从而
由
因
同理
将(4.2) 式代入(4.5) 式得
矛盾. 因此,
5 行波解的不存在性
5.1 情形Ⅰ: {\cal R}_0>1 0<c<c_\ast
本小节证明
引理5.1 设
且
证 由
其中
定义
对(5.1) 和(5.2)式在
将(5.4)式代入(5.3) 式得
因此
同理可得
令
又因
所以, 存在充分大的
令
由
对(2.2) 式的第一个方程从
因
设
利用常数变易法得
因此, 存在
引理得证.
下面给出定理2.2的证明.
定理2.2的证明 反证. 对
对任意
记
其中
根据文献[24]知,
令
同理得
对上面两方程作Laplace变换得
其中
和
这里
不难知
且
将(5.11) 式和(5.12) 式相乘得
这显然与引理3.1(ⅰ) 矛盾. 因而, 结论成立. 定理2.2得证.
5.2 情形Ⅱ: {\cal R}_0\leq1 c>0
本小节证明当
定理2.3的证明 反证, 假设系统存在一有界正解
(ⅰ) 首先考虑
且
其中
同理
对(5.15) 式两端积分得
同理, 对(5.16) 式有
将(5.18) 式代入(5.17) 式得
矛盾, 即假设不成立, 从而当
(ⅱ) 再考虑
取序列
为了推出矛盾, 下证
且
其中
因
6 最小波速 c_\ast
本节探讨登革热病毒潜伏期及染病人和蚊子的扩散率对临界波速
根据引理3.1知, 存在
(A) 先探究
因
图 2
图 2
最小波速
(B) 再探讨
7 总结
由于登革病毒在人和蚊子体内具有潜伏期, 并且人群和蚊子在空间中的随机移动需要耗费时间. 受此启发, 为了考虑不同扩散性和潜伏期对疾病传播的影响, 本文研究了一类具有离散时滞的反应扩散登革热模型行波的存在性和不存在性, 证明了(ⅰ) 当
参考文献
The global distribution and burden of dengue
DOI:10.1038/nature12060 [本文引用: 1]
Refining the global spatial limits of dengue virus transmission by evidence-based consensus
DOI:10.1371/journal.pntd.0001760
A time-periodic and reaction-diffusion Dengue fever model with extrinsic incubation period and crowding effects
DOI:10.1016/j.nonrwa.2019.102988
Analysis of a dengue disease transmission model
DOI:10.1016/S0025-5564(98)10003-2 [本文引用: 1]
A reaction-diffusion malaria model with incubation period in the vector population
Threshold dynamics of a vector-borne disease model with spatial structure and vector-bias
A nonlocal and time-delayed reaction-diffusion model of dengue transmission
DOI:10.1137/090775890 [本文引用: 1]
A reaction-diffusion model of vector-borne disease with periodic delays
DOI:10.1007/s00332-018-9475-9 [本文引用: 2]
Front propagation in periodic excitable media
DOI:10.1002/cpa.3022 [本文引用: 1]
Travelling wave solutions in mltigroup age-structured epidemic models
A geometric approach in the study of traveling waves for some classes of non-monotone reaction-diffusion systems
一类带治疗项的非局部扩散SIR传染病模型的行波解
DOI:10.3969/j.issn.1003-3998.2020.01.008
Traveling waves in a nonlocal dispersal SIR epidemic model with treatment
DOI:10.3969/j.issn.1003-3998.2020.01.008
Travelling wave fronts in reaction- diffusion systems with spatio-temporal delays
Minimal wave speed for a class of non-cooperative reaction-diffusion systems of three equations
DOI:10.1016/j.jde.2016.12.017 [本文引用: 2]
Minimal wave speed for a class of non-cooperative diffusion-reaction system
Traveling wave solutions in a two-group epidemic model with latent period
一类具有非线性发生率与时滞的非局部SIR模型的行波解
DOI:10.3969/j.issn.1003-3998.2018.03.008
Traveling waves in a nonlocal dispersal SIR epidemic model with delay and nonlinear incidence
DOI:10.3969/j.issn.1003-3998.2018.03.008
Traveling wave solutions of a diffusive SEIR epidemic model with nonlinear incidence rate
Basic reproduction numbers for reaction-diffusion epidemic models
Basic reproduction ratios for periodic compartmental models with time delay
Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission
DOI:10.1016/S0025-5564(02)00108-6 [本文引用: 1]
Existence, uniqueness, monotonicity and asymptotic behaviour of travelling waves for epidemic models
DOI:10.1088/0951-7715/26/1/121 [本文引用: 2]
Traveling waves for a diffusive SEIR epidemic model with non-local reaction
DOI:10.1016/j.apm.2017.05.040 [本文引用: 1]
Traveling wavefronts for delayed reaction-diffusion systems via a fixed point theorem
DOI:10.1006/jdeq.2000.3846 [本文引用: 1]
Existence of traveling wave solutions of a deterministic vector-host epidemic model with direct transmission
DOI:10.1016/j.jmaa.2020.123995 [本文引用: 2]
Travelling waves of a diffusive Kermack-McKendrick epidemic model with non-local delayed transmission