On gas jets
1
1904
... 其中, \beta 是常数, 表示Coulomb-like摩擦项, \alpha> 0 表示恒耗散系数, \rho 表示密度, u 表示速度, 以及 p(\rho) 表示流体压力, 且非线性方程 p(\rho)=\frac{\theta}{2}\rho^{\gamma-1}, 其中 \theta=\frac{\gamma-1}{2} , \gamma\in(1, 2) 是常数. 绝热指数 \gamma 在不同的情况下起着重要作用, 例如当 \gamma=-1 , p(\rho)=-\frac{1}{2\rho^{2}} 称为Chaplygin气体压力, 这是Chaplygin[1], Tsien[2]和von Karman[3]为了计算飞机机翼上升力的数值近似而引入的. ...
Two dimensional subsonic flow of compressible fluids
1
1939
... 其中, \beta 是常数, 表示Coulomb-like摩擦项, \alpha> 0 表示恒耗散系数, \rho 表示密度, u 表示速度, 以及 p(\rho) 表示流体压力, 且非线性方程 p(\rho)=\frac{\theta}{2}\rho^{\gamma-1}, 其中 \theta=\frac{\gamma-1}{2} , \gamma\in(1, 2) 是常数. 绝热指数 \gamma 在不同的情况下起着重要作用, 例如当 \gamma=-1 , p(\rho)=-\frac{1}{2\rho^{2}} 称为Chaplygin气体压力, 这是Chaplygin[1], Tsien[2]和von Karman[3]为了计算飞机机翼上升力的数值近似而引入的. ...
Compressibility effects in aerodynamics
1
1941
... 其中, \beta 是常数, 表示Coulomb-like摩擦项, \alpha> 0 表示恒耗散系数, \rho 表示密度, u 表示速度, 以及 p(\rho) 表示流体压力, 且非线性方程 p(\rho)=\frac{\theta}{2}\rho^{\gamma-1}, 其中 \theta=\frac{\gamma-1}{2} , \gamma\in(1, 2) 是常数. 绝热指数 \gamma 在不同的情况下起着重要作用, 例如当 \gamma=-1 , p(\rho)=-\frac{1}{2\rho^{2}} 称为Chaplygin气体压力, 这是Chaplygin[1], Tsien[2]和von Karman[3]为了计算飞机机翼上升力的数值近似而引入的. ...
The Riemann problem for the pressureless Euler system with the Coulomb-like friction term
2
2016
... Shen[4]研究具有Coulomb-like摩擦项的零压欧拉方程组, 并通过变量代换 ...
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Exact solution for granular flows
2
2012
... 获得其非自相似解. Faccanoni和Mangeney[5]首次通过引入变量代换(1.2)研究具有Coulomb-like摩擦项的浅水方程组的Riemann问题. ...
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
On the mathematical theory of sound
2
1858
... 如果 \alpha=0 和 \beta=0 , 则系统(1.1)为齐次可压缩流体欧拉方程组[6−9] ...
... 系统(1.3)是Earnshaw[6]于1858年首次用于研究等熵流体, 具有不同的物理背景. 例如, 它是具有远距离相互作用的牛顿动力学标度极限系统, 用于质量在 {\Bbb R} 中的连续分布[10−11], 同时也是Vlasov方程的流体动力的极限[12]. ...
Existence of global entropy solutions to a nonstrictly hyperbolic system
2
2005
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
... [7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Global entropy solutions to a variant of the compressible Euler equations
1
2008
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids
2
1981
... 如果 \alpha=0 和 \beta=0 , 则系统(1.1)为齐次可压缩流体欧拉方程组[6−9] ...
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
On the connection between Hamiltonian many-particle systems and the hydrodynamical equation
1
1991
... 系统(1.3)是Earnshaw[6]于1858年首次用于研究等熵流体, 具有不同的物理背景. 例如, 它是具有远距离相互作用的牛顿动力学标度极限系统, 用于质量在 {\Bbb R} 中的连续分布[10−11], 同时也是Vlasov方程的流体动力的极限[12]. ...
An integro-differential equation modelling a Newtonian dynamics and its scaling limit
1
1997
... 系统(1.3)是Earnshaw[6]于1858年首次用于研究等熵流体, 具有不同的物理背景. 例如, 它是具有远距离相互作用的牛顿动力学标度极限系统, 用于质量在 {\Bbb R} 中的连续分布[10−11], 同时也是Vlasov方程的流体动力的极限[12]. ...
Hydrodynamic limits of the Vlasov equation
1
1993
... 系统(1.3)是Earnshaw[6]于1858年首次用于研究等熵流体, 具有不同的物理背景. 例如, 它是具有远距离相互作用的牛顿动力学标度极限系统, 用于质量在 {\Bbb R} 中的连续分布[10−11], 同时也是Vlasov方程的流体动力的极限[12]. ...
Riemann problem for the Chaplygin Euler equations of compressible fluid flow
1
2010
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Global solutions to a class of nonlinear hyperbolic systems of equations
2
1973
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
... [14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Existence in the large for certain systems of quasi linear hyperbolic conservation laws
1
1982
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Delta shock wave to the compressible fluid flow with the generalized Chaplygin gas
0
2018
The multiplication of distributions in the study of a Riemann problem in fluid dynamics
1
2017
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Existence of global weak solutions to a special system of Euler equation with a source (Ⅱ): General case
1
2009
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
Concentration of mass in the pressureless limit of the Euler equations of one-dimensional compressible fluid flow
0
2020
The limits of Riemann solutions to Euler equations of compressible fluid flow with a source term
1
2020
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
The motion of a finite mass of granular material down a rough incline
1
1989
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
The Riemann problem for the Chaplygin gas equations with a source term
1
2016
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
The exact Riemann solutions to the generalized Chaplygin gas equations with friction
1
2016
... 下面让我们把注意力放在系统(3.1)的基本波上. 我们首先用稀疏波作为基本解. 我们知道如果 \alpha=0 和 \beta=0 , 也就是说, 在齐次情况下, 存在自相似解 (\rho, v)(t, x)=(\rho, v)(\xi) (\xi=x/t) . 但是现在情况则不存在像齐次情形那样的经典自相似解 (\rho, v)(x/t) . 在这种情况下, 解决方法必须另辟蹊径. 由于稀疏波是一种满足系统(3.1)的连续解, 可以通过确定每个特征场的积分曲线得到. 注意到 k - 黎曼不变量 (k = 1, 2) 在 k -稀疏波中是守恒的.因此, 就像文献[23]一样, 我们仍然可以使用稀疏波作为基本解. ...
Shadow waves for pressureless gas balance laws
0
2016
Non-classical shallow water flows
1
2008
... 如果取 u_{a}=-1 , 则系统(1.4)涵盖了重要的欧拉液滴模型[34−39]. 此外, 如果 \alpha=0 和 \beta=-1 , 那么系统(1.4) 在文献[25]中模拟了具有大弗劳德数浅流中的剧烈不连续性. ...
The limit behavior of the Riemann solutions to the generalized Chaplygin gas equations with a source term
0
2017
The vanishing pressure limits of Riemann solutions to the Chaplygin gas equations with a source term
0
2017
Riemann problems for a class of coupled hyperbolic systems of conservation laws with a source term
0
2019
The Riemann problem for the Suliciu relaxation system with the double-coefficient Coulomb-like friction terms
0
2019
Zero-exponent limit to the extended Chaplygin gas equations with friction
0
2021
Concentration in the flux approximation limit of Riemann solutions to the extended Chaplygin gas equations with friction
0
2019
Existence and stability of Riemann solution to the Aw-Rascle model with friction
0
2018
The vanishing adiabatic exponent limits of Riemann solutions to the isentropic Euler equations for power law with a Coulomb-like friction term
1
2019
... 许多学者已深入研究系统(1.3)的解[7−9, 13−20]. 特别的, DiPerna[14]首次使用Glimm方法对 1 <\gamma<3 情形的Cauchy问题研究全局弱解的存在性定理. Li[15]在DiPerna[14]研究的基础上获得 -1 < \gamma < 1 情形的Cauchy问题全局弱解. Lu[7]和Cheng[8]基于补偿紧致性理论和动力学方程的基本思想, 分别研究 \gamma > 3 , 1 <\gamma < 3 情形的Cauchy问题的全局熵解的存在性定理. 对压力 p 为在实轴上取实值的一整函数情形, Sarrico[17]构造性的得到Riemann问题在含间断函数和Dirac测度的广义函数的适当的空间中解. 对压力 p(\rho)=\int^{\rho}_{0}s e^{s}{\rm d}s 情形, Song and Xiao[18]研究带有源项的系统(1.3)的Cauchy问题全局弱解的存在性定理. 因此, 研究具有源项的可压缩流体流动欧拉方程组的解, 如摩擦、阻尼和松弛效应是很自然的. 这里, 我们集中讨论(1.1)式中提出的源项. 如果 \alpha=0 , 那么这种源项, 有时被称为Coulomb-like摩擦项, 是Savage和Hutter[21]早期提出来描述颗粒流动行为的. 目前, 对一些具有Coulomb-like摩擦项的双曲型方程组解的数学研究非常活跃, 有兴趣的读者可以参考文献[4−5, 22−33]. ...
A finite element method study of Eulerian droplets impingement models
1
1999
... 如果取 u_{a}=-1 , 则系统(1.4)涵盖了重要的欧拉液滴模型[34−39]. 此外, 如果 \alpha=0 和 \beta=-1 , 那么系统(1.4) 在文献[25]中模拟了具有大弗劳德数浅流中的剧烈不连续性. ...
Eulerian droplet model: Delta-shocks and solution of the Riemann problem
0
2019
Eulerian models with particle pressure for air-particle flows
1
2019
... 如果取 u_{a}=-1 , 则系统(1.4)涵盖了重要的欧拉液滴模型[34−39]. 此外, 如果 \alpha=0 和 \beta=-1 , 那么系统(1.4) 在文献[25]中模拟了具有大弗劳德数浅流中的剧烈不连续性. ...
Formation of δ -shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids
2
2003
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
... 在文献[40−43]的激励下, 本文研究了可压缩流体流动的非齐次欧拉方程组(1.1)的黎曼解当绝热指数趋于1时的极限. 与齐次方程不同, 黎曼解是非自相似的, 当 \gamma \rightarrow1 时, 我们发现在 1 < \gamma < 2 的情况下, 也存在相同的质量集中现象和真空现象. ...
Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids
1
2004
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
Note on the compressible Euler equations with zero temperature
1
2001
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
Concentration of mass in the pressureless limit of Euler equations for power law
2
2019
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
... 在文献[40−43]的激励下, 本文研究了可压缩流体流动的非齐次欧拉方程组(1.1)的黎曼解当绝热指数趋于1时的极限. 与齐次方程不同, 黎曼解是非自相似的, 当 \gamma \rightarrow1 时, 我们发现在 1 < \gamma < 2 的情况下, 也存在相同的质量集中现象和真空现象. ...
Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas
1
2016
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
The limits of Riemann solutions to the isentropic magnetogasdynamics
0
2011
Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model
0
2010
Limit relations for three simple hyperbolic systems of conservation laws
0
2010
Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state
0
2020
The limits of Riemann solutions for the isentropic Euler system with extended Chaplygin gas
0
2019
Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes
0
2015
The limits of Riemann solutions to the simplified pressureless Euler system with flux approximation
0
2018
Delta shocks and vacuum states in vanishing pressure limits of solutions to the isentropic Euler equations for modified Chaplygin gas
0
2014
Flux approximation to the isentropic relativistic Euler equations
0
2016
Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases
0
2009
Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations
0
2008
Delta wave formation and vacuum state in vanishing pressure limit for system of conservation laws to relativistic fluid dynamics
0
2015
Flux-approximation limits of solutions to the relativistic Euler equations for polytropic gas
0
2016
Delta-shocks and vacuums in the relativistic Euler equations for isothermal fluids with the flux approximation
1
2019
... 当压力趋于零或常数时, 欧拉方程组(1.5)收敛到零压气体动力学系统. 在早期的开创性论文中, Chen和Liu[40]通过在模型 p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1) 中取极限 \varepsilon \rightarrow 0+ , 首次证明了多方气体欧拉方程组(1.5) 的Riemann解的delta激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还得到了文献[41]中非等熵流体欧拉方程相同的结果.Li[42]研究了欧拉方程(1.5) 对等温情形 (\gamma = 1) 的相同问题. 最近, 当 \gamma \rightarrow 0 , 即压力趋于常数时, Ibrahim等人在文献[43]中证明了集中现象也存在于模型 p(\rho) =\rho^{\gamma} (0 < \gamma < 1) . 也就是说, 他们用欧拉方程(1.5)的黎曼解的极限行为严格地证明了delta激波的形成. 对于其他一些物理模型, 也有许多结果[44−58]. ...
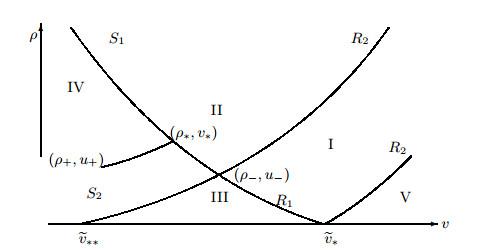
1
... 在本节, 我们给出系统(1.4)的Riemann问题的解. 对于系统(1.4)相应的齐次型系统, Riemann问题的解可参考文献[59, 60]. ...
A Riemann problem whose viscosity solutions contain delta measures
1
1993
... 在本节, 我们给出系统(1.4)的Riemann问题的解. 对于系统(1.4)相应的齐次型系统, Riemann问题的解可参考文献[59, 60]. ...