1 引言
设
其中
在
最近, 郭丹妮和蔡钢[13]提出了如下投影算法
其中
受到上述工作的启发, 本文提出了新的一步投影算法, 找到了变分不等式解集与半压缩映射不动点集的一个公共元. 在伪单调和一致连续条件下, 证明了新算法的强收敛定理. 通过数值实验可以发现, 我们得到的结果推广和提高了许多最新的结果.
2 相关定义与引理
记
任给
定义2.1 设
(ⅰ)
(ⅱ)
其中
(ⅲ)
(ⅰ)
(ⅱ)
事实上, 上述定义等价于
也等价于
若
引理2.1[17] 设
引理2.2[18] 设
引理2.3[19] 设
引理2.4[20] 设
本文假设
3 算法与收敛性证明
本文提出如下算法:
算法3.1 选取
步骤1 计算
其中
步骤2 计算
其中
步骤3 计算
令
引理3.1 假设
证 证明过程类似于文献[8]中引理3.1的证明过程, 故这里不再赘述.
引理3.2 假设
证 由
即
从而
下证
考虑以下两种情形: 首先考虑
现考虑
故
根据线搜索准则(3.1)知
即
联立(3.4)和(3.5)式可得
在上式中令
另一方面, 观察到
由
联立(3.3)和(3.6)式可得
下证
由
易知
根据
下证
由
故
因此, 对任意的
根据文献[21]中引理2.1可知
定理3.1 假设
证 该定理的证明分为以下三步进行.
第一步: 设
事实上, 由
由
又因为
联立(3.10)–(3.12)式可得
从而(3.9)式得证.
第二步: 证明
观察到
因为
由
第三步: 证明算法3.1迭代产生的序列
故算法3.1迭代产生的序列
定理3.2 假设
证 该定理的证明分为以下三步进行.
第一步: 证明
观察到
将(3.13)和(3.16)式代入(3.18)式得
由此可得(3.17)式成立.
第二步: 证明
事实上
由于
故(3.19)式成立.
第三步: 证明序列
情形1 若存在正整数
另一方面
根据(3.21)式可得
联立(3.21)和(3.23)式有
对于
注意到
结合(3.24)–(3.26)式可得
因为
下证:
由
注意到
因此, 由(3.27)式可得
由(3.19)式和引理2.4可得
情形2 若存在
根据(3.17)式可得
由假设条件可得
类似情形1的证明可得
由(3.20)式可得
从而
由(3.28)–(3.30)式得
即算法3.1迭代产生的序列
注3.1 定理3.2从以下三个方面改进了文献[12]中定理3.5:
(ⅰ) 映射
(ⅱ)
(ⅲ) 算法3.1中步长的选取与文献[12]中算法3.2不同. 事实上, 我们的步长选择更优.
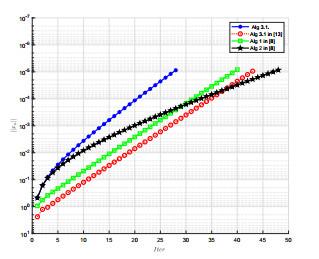
4 数值实验
例4.1 设映射
其中
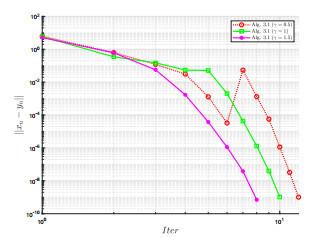
图 1
图 2
图 2
例1
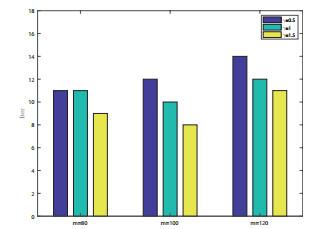
表 1
例4.1
| Iter | CPU time | Iter | CPU time | Iter | GPU time | |||
| 51 | 0.8511 | 52 | 0.7227 | 52 | 0.7869 | |||
| 53 | 0.7082 | 58 | 0.8453 | 62 | 0.9145 | |||
| 55 | 0.7157 | 53 | 0.6831 | 57 | 0.9798 | |||
| 236 | 5.7441 | 318 | 9.4689 | 427 | 19.516 | |||
例4.2 设映射
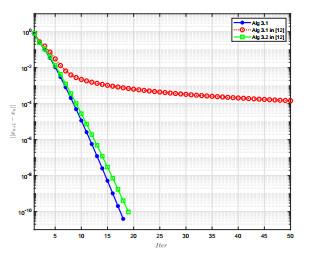
图 3
图 4
表 2
例4.2
例4.3 设映射
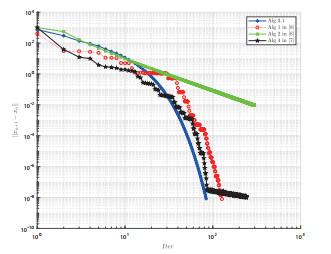
图 5
图 6
表 3 例4.3不同误差界下3种算法的比较
例4.4 假设
图 7
图 8
表 4 例4.4不同误差界下4中算法的比较
注4.1 从数值实验的结果来看, 我们有如下结论:
(ⅲ) 由表 2可知,
参考文献
Convex programming in Hilbert space
DOI:10.1090/S0002-9904-1964-11178-2 [本文引用: 2]
A modified forward-backward splitting method for maximal monotone mappings
DOI:10.1137/S0363012998338806 [本文引用: 1]
Weak and strong convergence of inertial Tseng's extragradient algorithms for solving variational inequality problems
DOI:10.1080/02331934.2020.1789129 [本文引用: 6]
Modified Tseng's extragradient methods for solving pseudo-monotone variational inequalities
DOI:10.1080/02331934.2019.1616191 [本文引用: 18]
Strong convergence result for solving monotone variational inequalities in Hilbert space
An extragradient method for solving variational inequalities without monotonocity
DOI:10.1007/s10957-020-01791-x [本文引用: 1]
Mann-type algorithms for variational inequality problems and fixed point problems
DOI:10.1080/02331934.2019.1692207 [本文引用: 1]
Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems
DOI:10.1007/s11075-018-0626-8 [本文引用: 16]
Hybrid inertial subgradient extragradient methods for variational inequalities and fixed point problems involving asymptotically nonexpansive mappings
DOI:10.1080/02331934.2019.1647203 [本文引用: 1]
Complementarity problems over cones with monotone and pseudomonotone maps
DOI:10.1007/BF00932654 [本文引用: 1]
Iterative methods for the computation of fixed points of demicontractive mappings
DOI:10.1016/j.cam.2010.01.050 [本文引用: 1]
Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators
DOI:10.1007/s10559-015-9768-z [本文引用: 1]
A hybrid extragradient-viscosity method for monotone operators and fixed point problems
DOI:10.1137/060675319 [本文引用: 1]
Iterative algorithms for nonlinear operators
DOI:10.1112/S0024610702003332 [本文引用: 1]
Pseudo-monotone complementarity problems in Hilbert space
DOI:10.1007/BF00941468 [本文引用: 1]