1 引言
Saint-Venant方程组由Saint-Venant于1871年提出[1], 至今仍在浅水流、涌浪传播、水库和明渠流等问题的数值求解中发挥着重要作用. 在一维情形下, 其向量形式可表示为
其中
该方程组的一个重要特征是其满足稳态解
其中
Nessyahu和Tadmor于1990年提出了用于求解双曲守恒律问题的二阶交错中心格式[2], 相较于迎风格式, 其优势在于避免了求解黎曼问题, 但于相邻时间层, 数值解会在交错单元与非交错单元之间来回更替, 导致了复杂的边界条件设置. 为此, Touma提出了稳健的二阶非交错中心格式[3], 并将其应用于Saint-Venant方程组, 提出了保正的能维持静稳态解的格式[4], 但在干湿界面处, “保正性”与“和谐性”无法同时得到满足. Dong和Li[5]通过重构守恒变量及水位值, 且在干湿界面处构造关于水位的映射, 使格式在干湿界面处经过“保正性”处理后仍可维持静稳态解. 然而在用中心格式求解移动稳态问题时, 在底部地形变化处(
本文提出了一种具有二阶精度的能够精确维持移动稳态解的非交错中心格式. 一方面, 基于移动稳态解的特征, 选择重构守恒变量以及能量值, 并通过求解非线性方程得到基于稳态时的水深; 另一方面, 在对守恒变量进行时间层的更新时, 基于稳态时的能量, 提出了一种新的源项离散方法, 使其能够平衡非零通量的梯度, 以保证格式的“和谐性”.
文章的结构如下, 第2节, 对格式做详细叙述, 包括经典格式的回顾, 新格式的构造以及“和谐性”的证明; 第3节, 通过一些经典的数值算例验证了格式的收敛性, 和谐性及稳健性; 第4节, 对格式做出总结.
2 维持移动稳态解的非交错中心格式
2.1 经典的非交错中心格式
针对Saint-Venant方程组的初值问题, 先简要介绍一下经典的非交错中心格式. 将计算区域
是已知的.
(1) 向前投影
为了获得二阶精度且避免虚假震荡, 对
其中
其中
利用上述分片线性函数
(2) 预测步
将方程(1.1)在矩形
在
其中
由(2.2)式即可得
其中,
(3) 向后投影
同理于向前投影, 可求得
2.2 新的非交错中心格式
(1) 底部函数处理
将底部地形函数
其中
若
(2) 向前投影
为维持移动稳态解, 首先计算每个非交错单元
对
其中,
如果
由此得到
(3) 向后投影
类似于向前投影, 首先计算每个交错单元
再对
如果
(4) 非线性方程求解
考虑上述过程所牵涉到的非线性代数方程
其解不唯一, 解法如下:
(Ⅰ) 如果
(Ⅱ) 如果
其中
这里面有一个负根和两个正根, 舍弃负根, 通过以下方法来选取符合物理现象的根:
引入弗劳德数
2.3 源项的"和谐性"离散
(1) 源项离散
首先考虑(2.3)式, 注意到
其中,
其中
其中
再考虑(2.2)式关于源项积分的逼近:
其中
注意到(2.10)式第一项用的是中心差分及中点积分公式, 且对于光滑解, 第二项有
故此数值积分也有二阶精度.
(2) "和谐性"的证明
定理2.1 假设在
则(Ⅰ)由(2.3)式得到的预测值
证 首先来证明(Ⅰ), 不妨设
将(2.12)式代入(2.3)式
当
接下来证明(Ⅱ), 由(Ⅰ), (2.2)式变成
其中
由于
将(2.14)式代入(2.13)式, 有
由(2.10)式, 有
故
定理2.2 在定理2.1的条件下, 利用向前投影(2.5)以及向后投影(2.7), 本文提出的非交错中心格式是具有“和谐性”的, 即
证 不妨设相邻三个非交错单元
又由minmod参数
也就是说对于相邻两个交错单元
且对于非交错单元
注2.1 为了避免在(临近)干湿界面处水深趋近于0而导致速度变得异常的大, 格式采取文献[6]中的去奇异性策略:
为保持一致性, 重新计算
3 数值算例
本节主要展示所提出的维持移动稳态的非交错中心格式(新格式)在一些经典算例上的数值结果, 并将其与文献[5]中的格式(旧格式)进行比较, 以展现新格式在求解移动稳态问题时的优势. 取重力加速度
首先检验格式在数值上是否二阶收敛, 取底部函数为
初值条件为
表 1
水深的
| 网格数 | 收敛阶 | |
| 50 | - | |
| 100 | 2.00 | |
| 200 | 2.01 | |
| 400 | 2.00 |
3.1 维持移动稳态算例
本例验证格式能否维持移动稳态解. 取底部函数为
初值条件分为以下三种情形[6]:
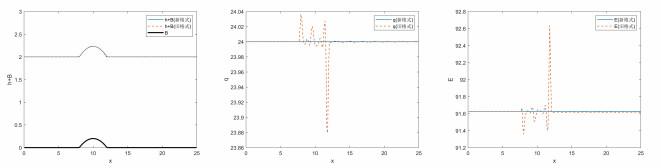
(a) 超临界流:
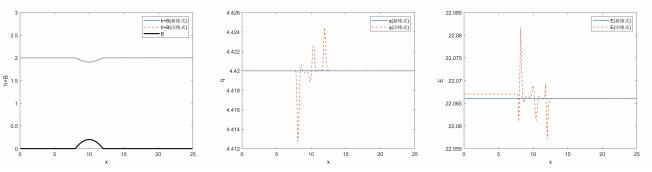
(b) 次临界流:
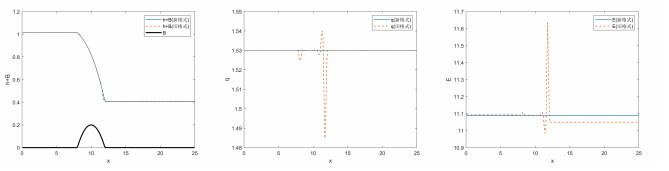
(c) 跨临界流:
计算区域为
注3.1 本例的初值条件给的是
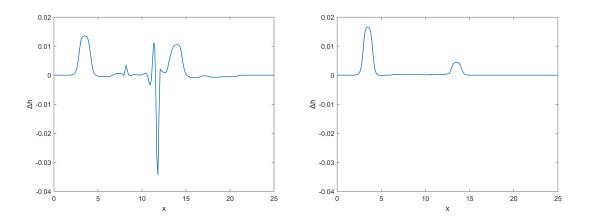
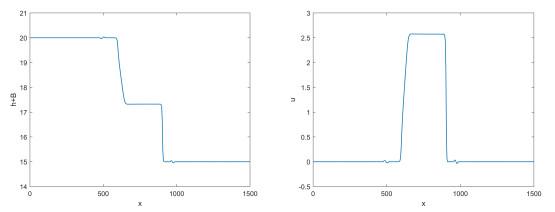
3.2 捕捉移动稳态小扰动算例
本例测试格式捕捉小扰动的能力. 在例3.1的条件下, 当
图 1
图 2
图 3
注3.2 本例忽略了(2.4)和(2.6)式中计算
3.3 收敛到移动稳态算例
本例测试格式能否收敛到例3.1中的移动稳态. 初边值条件如下[6]:
(a) 超临界流:
(b) 次临界流:
(c) 跨临界流:
图 4
图 5
图 6
注3.3 情形(c)的下游边值条件(
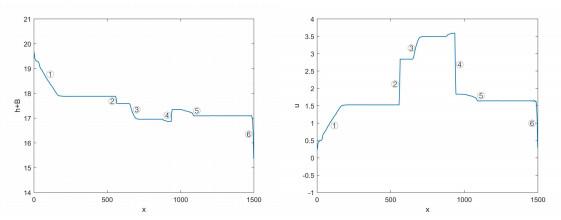
3.4 溃坝算例
本例用格式模拟实际生活中经常遇到的溃坝问题. 第一个算例模拟的是在含矩形凸起的地形上溃坝水流的流动[9], 取底部函数为
初值条件为
图 7
图 8
第二个算例模拟的是含有干湿界面的溃坝水流的流动[6], 将例3.3中情形(a)的初值条件改为
边值条件不变, 网格数200. 图 9给出了输出时间
图 9
4 总结
本文针对一维Saint-Venant方程组, 提出了一种新的非交错中心有限体积格式. 通过对守恒变量以及能量值的分片线性重构, 使得格式具有二阶精度, 且当流体处于移动稳态时, 能够在向前及向后投影时维持流量与能量的不变性, 再求解非线性方程得到基于稳态时的水深; 通过一种新的源项离散方法, 使格式能维持移动稳态解. 格式很好地避免了经典中心格式在求解移动稳态问题时出现较大误差这一问题. 最后通过数值算例, 验证了该格式的和谐性及稳健性.
参考文献
Théorie du mouvement non-permanent des eaux avec application aux crues des rivires et à lintroduction des marées dans leur lit
Non-oscillatory central differencing for hyperbolic conservation laws
DOI:10.1016/0021-9991(90)90260-8 [本文引用: 3]
Central unstaggered finite volume schemes for hyperbolic systems: applications to unsteady shallow water equations
Well-balanced central schemes for systems of shallow water equations with wet and dry states
DOI:10.1016/j.apm.2015.09.073 [本文引用: 3]
An effect non-staggered central scheme based on new hydrostatic reconstruction
DOI:10.1016/j.amc.2019.124992 [本文引用: 2]
Moving-water equilibria preserving central-upwind schemes for the shallow water equations
DOI:10.4310/CMS.2016.v14.n6.a9 [本文引用: 6]
A new approach for designing moving-water equilibria preserving schemes for the shallow water equations
DOI:10.1007/s10915-019-00947-w [本文引用: 1]
Moving-water equilibria preserving partial relaxation scheme for the Saint-Venant system
DOI:10.1137/19M1258098 [本文引用: 1]
High-order well-balanced finite volume WENO schemes for shallow water equation with moving water
DOI:10.1016/j.jcp.2007.03.031 [本文引用: 2]
On the advantage of well-balanced schemes for moving-water equilibria of the shallow water equations
Exactly well-balanced discontinuous Galerkin methods for the shallow water equations with moving water equilibrium
DOI:10.1016/j.jcp.2013.10.010 [本文引用: 1]
A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system
DOI:10.4310/CMS.2007.v5.n1.a6 [本文引用: 2]
A new hydrostatic reconstruction scheme based on subcell reconstructions
High-resolution nonoscillatory central schemes with nonstaggered grids for hyperbolic conservation laws
Unstaggered central schemes with constrained transport treatment for ideal and shallow water magnetohydrodynamics
DOI:10.1016/j.apnum.2010.02.006
Well-balanced unstaggered central schemes for one and two-dimensional shallow water equation systems
A well-balanced reconstruction for wet/dry fronts for the shallow water equations
DOI:10.1007/s10915-012-9677-5 [本文引用: 1]