炭疽是由革兰氏阳性杆状细菌即炭疽杆菌引起的一种严重的传染病.该疾病既传染人又传染动物.当孢子进入人体时, 人就会感染.家畜和野生动物吸入污染的土壤, 植物或水时也会感染该疾病.尽管炭疽普遍发生在发展中国家^[1], 但是世界各地均有炭疽疾病的发生.感染炭疽之后, 食草动物如牛和羊会突然死亡, 造成巨大的经济损失.在有家畜感染炭疽的地方, 对动物提前进行接种可以预防炭疽的爆发^[2].

已有一些数学模型对炭疽的传播进行了研究.比如, Hahn和Furniss^[3]建立了一个微分方程模型来研究封闭环境中(种群没有出生和死亡)对环境消毒对控制炭疽传播的有效性.近年来, Friedman和Yakubu^[4]把文献[3]中的模型拓展为一个偏微分方程模型, 该模型中加入了动物种群的迁移、出生和死亡因素.为了研究炭疽潜伏期的影响, Mushayabasa等^[5]建立了一个具有潜伏期的炭疽模型, 研究了模型的动力学行为.此外, Mushayabasa^[6]提出了一个具有分布时滞的炭疽模型, 模型中的分布时滞表示动物的不同潜伏期. Saad-Roy等^[7]拓展了文献[4]中没有扩散的模型, 给出了炭疽疾病的持久和灭绝性.

尽管已有许多模型对炭疽疾病进行了研究, 但是炭疽的周期性爆发并没有引起人们的重视.人们在食草野生动物中已经观察到了炭疽病例的季节性高峰^{[8, 9]}.因此本文将建立一个具有季节性的时滞炭疽模型.

假设动物种群被分为三个仓室:易感者$S(t)$, 潜伏者$E(t)$和染病者$I(t)$.令$B(t)$和$P(t)$分别表示环境中孢子和染病动物尸体的数量.与文献[10]一样, 假设动物种群遵循Beverton-Holt增长, 假定所有的新生动物均为易感者, 即动物的增长率为

其中内禀增长率为$r(t)>0$, 尺度参数为$b(t)>0$, $N(t)=S(t)+E(t)+I(t)$为动物的总数量.假定炭疽在动物体内的平均潜伏期为$\tau$.令$\mu(t)$, $\alpha(t)$为动物的自然死亡率和因病死亡率.假设$\beta(t)$表示环境中孢子对动物的传染率, $\eta(t)$为每一具尸体产生的孢子的增长率.令$\delta(t)$和$k(t)$分别表示孢子和动物尸体的衰减率.根据以上假设得到如下模型

为了考虑炭疽爆发的季节性, 假设模型(2.1)中的所有参数均为正的, $\omega$周期的连续函数, $\omega>0$, $\tau$为非负常数.

对一个连续的$\omega$周期函数$g(t)$, 定义

为了避免动物种群灭绝, 在本文中给出如下假设

($\rm H1$) $\bar{r}>\bar{\mu}, \, \, \forall t\geq 0.$

考虑线性系统

由文献[11]中的定理3.2可以得到下面的结论.

引理2.1  假设(H1)成立.则方程(2.2)有一个全局吸引的正的$\omega$周期解$x^*(t)$.

令$C=C([-\tau, 0], {{\Bbb R}} ^5)$, $C^+=C([-\tau, 0], {{\Bbb R}} ^5_{+})$.则$(C, C^{+})$是一个序巴拿赫空间.对任意给定的连续函数$x: [-\tau, \sigma)\rightarrow {{\Bbb R}} ^5$, $\sigma>0$, 定义$x_t(\theta)=x(t+\theta)$, $\forall \theta\in[-\tau, 0]$, $\forall t\in[0, \sigma)$.

定义系统(2.1)初始值属于集合${\cal Z}$:

引理2.2  对任意的初值$\phi\in {\cal Z}$, 系统(2.1)有一个唯一的非负解$u_t(\phi)\in {\cal Z}$, $\forall t\geq0$, $u_0=\phi$, 且系统(2.1)的解是最终有界的.

证  给定$\phi\in {\cal Z}$, 定义$f(t, \phi)=(f_1(t, \phi), f_2(t, \phi), f_3(t, \phi), f_4(t, \phi), f_5(t, \phi))$如下

因为$f(t, \phi)$在$(t, \phi)\in {{\Bbb R}} _{+}\times {\cal Z}$上是连续的, 且在${\cal Z}$的每一个紧子集上$f(t, \phi)$关于$\phi$满足利普希茨条件, 因此系统(2.1)有一个唯一的解$u(t, \phi)$, $u_0=\phi$, 其最大存在区间记为$[0, \sigma_\phi)$ (见文献[12]中的定理2.2.1和2.2.3).

根据集合${\cal Z}$中关于$\phi_2$的相容性条件, 系统(2.1)中的第二个方程可以写为如下积分方程的形式

因此如果$u_i(t)\geq0$, $i=1, 4$, $t\in[0, m]\subseteq[0, \sigma_\phi)$, 则$u_2(t)\geq0$, $\forall t\in[0, m]$.令$\phi=(\phi_1, \phi_2, \phi_3, \phi_4, \phi_5)\in {\cal Z}$, 则如果$\phi_i(0)=0$, $i\in\{1, 3, 4, 5\}$, 有$f_i(t, \phi)\geq0$.根据文献[13]中的定理5.2.1知, 对所有的$t\in [0, \sigma_\phi)$, $\phi\in {\cal Z}$, $u_i(t, \phi)\geq0$, $i=1, 3, 4, 5$.由方程(2.3)得对所有的$t\in [0, \sigma_\phi)$, $E(t)\geq0$.因此, 对任意的$\phi\in {\cal Z}$, 系统(2.1)有一个唯一的非负解$u(t, \phi)$, $u_0=\phi$, 且对所有的$t\in[0, \sigma_\phi)$, $u(t, \phi)\in {\cal Z}$.

因为对所有的$t\in[0, \sigma_\phi)$, 有

则系统(2.1)由以下合作系统控制

由比较原理(见文献[13]中定理5.1.1)和引理2.1知, $\tilde{N}(t)$最终有界.因此系统(2.4)的解最终有界, 进而系统(2.1)的解在$[0, \infty)$上存在且最终有界.证毕.

易得系统(2.1)有一个唯一的无病周期解

其中$S^*(t)$是方程$\frac{{\rm d}N(t)}{{\rm d}t}=\frac{r(t)N(t)}{1+b(t)N(t)}-\mu(t)N(t)$的全局稳定的正的$\omega$周期解.在无病周期解$E_0(t)$处线性化系统(2.1), 得关于染病仓室$I(t)$, $B(t)$和$P(t)$的线性化系统

令$F: {{\Bbb R}} \rightarrow {\cal L}(C, {{\Bbb R}} ^3)$, $V(t)$是${{\Bbb R}}$上的一个连续的$3\times3$矩阵函数, 定义如下

设$\Phi(t, s)$为如下系统的演化矩阵

即

这里$I$是一个$2\times2$的单位矩阵.

令$C_\omega$为${{\Bbb R}}$到${{\Bbb R}} ^3$上的所有连续的$\omega$周期函数组成的序巴拿赫空间, 其正锥为

定义线性算子$L: C_\omega\rightarrow C_\omega$如下

由文献[14], 系统(2.1)的基本再生数$R_0$为$L$的谱半径, 即$R_0=r(L)$.

定义

则$({\cal Y}, {\cal Y}_{+})$是一个序巴拿赫空间.

设$P(t)$为系统(2.5)的解映射, 即$P(t)\phi=u_t(\phi)$, 这里$u(t, \phi)$是系统(2.5)唯一的解, $u_0=\phi\in {\cal Y}$.则$P:=P(\omega)$为系统(2.5)的庞加莱映射.令$r(P)$为$P$的谱半径.由文献[14]中定理2.1, 有如下结论:

引理2.3  $R_0-1$与$r(P)-1$有相同的符号.

下面证明$P(t): {\cal Y}_{+}\rightarrow {\cal Y}_{+}$是最终强单调的.

引理2.4  令$\varphi, \, \psi\in {\cal Y}_{+}$, $\varphi>\psi$ (即$\varphi\geq\psi$, $\varphi\neq\psi$), 则对于系统(2.5)分别具有初值$\bar{v}_0=\varphi$, $v_0=\psi$的解$\bar{v}(t)$和$v(t)$, 对所有的$t>\tau$, 有$\bar{v}_i(t)>v_i(t)$, $t>\tau$, $i=1, 2, 3$, 因此, 对所有的$t>2\tau$, 有$P(t)\varphi \gg P(t)\psi$.

证  由文献[13]中定理5.1.1知对所有的$t\geq0$, 有$\bar{v}(t)\geq v(t)$; 即$P(t):{\cal Y}_{+}\rightarrow {\cal Y}_{+}$是单调的.下证$P(t):{\cal Y}_{+}\rightarrow {\cal Y}_{+}$为最终强单调的.令$\bar{v}(t)=\bar{v}(t, \varphi)=(\bar{y}_1(t), \bar{y}_2(t), \bar{y}_3(t))$, $v(t)=v(t, \psi)=(y_1(t), y_2(t), y_3(t))$.不失一般性, 假定$\varphi_2>\psi_2$.

结论1  存在$t_0\in[0, \tau]$, 当$t\geq t_0$时, 有$\bar{y}_1(t)>y_1(t)$.

首先证明存在某个$t_0\in[0, \tau]$, 使得$\bar{y}_1(t_0)>y_1(t_0)$.否则$\forall t\in [0, \tau]$有$\bar{y}_1(t)=y_1(t)$, 因此$\frac{{\rm d}\bar{y}_1(t)}{{\rm d}t}=\frac{{\rm d}y_1(t)}{{\rm d}t}$, $\forall t\in (0, \tau)$.则

因此对所有的$t\in [0, \tau]$, 有$\bar{y}_2(t-\tau)=y_2(t-\tau)$, 即$\varphi_2(\theta)=\psi_2(\theta)$, $\forall\theta\in [-\tau, 0]$, 与$\varphi_2>\psi_2$矛盾.

令

因此

即

因此$\overline{y}_1(t_0)> y_1(t_0)$, 由常微分方程比较原理(参见文献[15, 定理4])知$\overline{y}_1(t)> y_1(t)$, $\forall t\geq t_0$.

结论2  当$t\geq t_0$时, $\bar{y}_3(t)>y_3(t).$

令$g_2(t, y)=(\mu(t)+\alpha(t))y_1(t)-k(t)y$.则有

因此

因为$\bar{y}_3(t_0)\geq y_3(t_0)$, 同样由文献[15]中定理4得$\bar{y}_3(t)> y_3(t)$, $\forall t>t_0$.

同理可以证明$\bar{y}_2(t)>y_2(t)$, $\forall t>t_0$.最终得

由于$t_0\in [0, \tau]$, 则$(\overline{y}_{1t}, \overline{y}_{2t}, \overline{y}_{3t})\gg (y_{1t}, y_{2t}, y_{3t})$, $\forall t>2\tau$, 即$v_t(\varphi)\gg v_t(\psi)$, $\forall t>2\tau$.因此对任意的$t>2\tau$, $P(t): {\cal Y}_{+}\rightarrow {\cal Y}_{+}$是强单调的.证毕.

由文献[12]中定理3.6.1知线性算子$P(t)$在${\cal Y}_{+}$上是紧的.选取整数$n_0>0$使得$n_0\omega>2\tau$.因为$P^{n_0}=P(n_0\omega)$, 则$r(P)$是$P$的一个简单特征值且有一个强正的特征向量(参见文献[16, 引理3.1]), 其他任意特征值的模小于$r(P)$.由文献[17, 引理1], 得到如下结果.

引理2.5  令$m=\frac{\ln r(P)}{\omega}$, 则存在一个正的$\omega$周期函数$v^*(t)$, 使得$e^{mt}v^*(t)$为系统(2.5)的一个正解.

本节研究系统(2.1)的全局动力学行为.下面的结果表明当$R_0<1$时疾病绝灭.

令

定理3.1  如果$R_0<1$, 则无病周期解$E_0(t)=(S^*(t), 0, 0, 0, 0)$在$X\setminus(\{(0, 0, 0)\} \times C([-\tau, 0], {{\Bbb R}} _{+})\times{{\Bbb R}} _{+})$内是全局吸引的.

证  首先考虑下面的扰动线性系统

令$P_\epsilon(t)$为系统(3.1)在空间${{\Bbb R}} \times C([-\tau, 0], {{\Bbb R}} )\times {{\Bbb R}}$上的解映射, $P_\epsilon:=P_\epsilon(\omega)$.因为$R_0<1$, 由引理2.3知, $\lim\limits_{\epsilon\rightarrow 0^+} r(P_\epsilon)=r(P)<1$.固定充分小的$\epsilon>0$, 使得$r(P_\epsilon)<1$.易证当$t>2\tau$时, 在${{\Bbb R}} \times C([-\tau, 0], {{\Bbb R}} )\times {{\Bbb R}}$上$P_\epsilon(t)$是紧的且最终强单调.由引理2.5知, 存在正的$\omega$周期函数$v_\epsilon(t)=(v_{\epsilon1}(t), v_{\epsilon2}(t))$, 使得$u_\epsilon(t)=e^{\frac{\ln r(P_\epsilon)}{\omega}t}v_\epsilon(t)$为(3.1)的正解.因为$\ln r(P_\epsilon)<0$, $v_\epsilon(t)$有界, 则当$t\rightarrow \infty$时$u_\epsilon(t)\rightarrow0$.

由比较原理和引理2.1知, 当$t$充分大时, $N^*(t)<S^*(t)+\epsilon$.选取充分大的整数$n_1>0$, $n_1\omega>\tau$, 使得当$t\geq n_1\omega-\tau$时有$N(t)<S^*(t)+\epsilon$.因此, 当$t\geq n_1\omega$时得

令$l> 0$充分大使得当$t\in[n_1\omega, n_1\omega+\tau]$时, $(I(t), B(t), P(t))\leq lu_\epsilon(t)$.由文献[13]中定理5.1.1知$(I(t), B(t), P(t))\leq lu_\epsilon(t)$, $\forall t\geq n_1\omega+\tau$.因此当$t\rightarrow \infty$时, $I(t)\rightarrow0$, $B(t)\rightarrow0$, $P(t)\rightarrow0$.则由渐近周期半流理论(参见文献[18, 定理3.2.1])知

证毕.

下面的结果表明当$R_0>1$时, 疾病是持久的.

定理3.2  如果$R_0>1$, 则系统(2.1)至少存在一个正的$\omega$周期解, 且存在常数$\xi>0$, 使得系统(2.1)具有初值条件$\phi \in X_0$的解$(S(t, \phi), E(t, \phi), I(t, \phi), B(t, \phi), P(t, \phi))$满足

证  令$Q(t)$为系统(2.1)在$X$上的解映射, 即$Q(t)\phi=u_t(\phi)$, $t\geq0$, 这里$u(t, \phi)$, $u_0=\phi\in X$为系统(2.1)的唯一解.则$Q:=Q(\omega)$是系统(2.1)的庞加莱映射.

由系统(2.1)的第三, 第四和第五式易知对任意的$t\geq0$, $Q(t)X_0\subseteq X_0$.由引理2.2知$\{Q^n: {\cal X}_{\delta_0}\rightarrow {\cal X}_{\delta_0}\}_{n\geq0}$为点耗散的, 且对充分大的$n$, $Q^n$为紧的.则由文献[19]中定理2.9知$Q$在$X$中有一个全局吸引子.下面证明$Q$关于$(X_0, \partial X_0)$是一致持续的.

令$M_1=(0, 0, 0, 0, 0)$, $M_2=(S^*(0), 0, 0, 0, 0)$.因为$S^*(t)$为正周期解, 选取充分小的正数$\varepsilon$使得

因为$\lim\limits_{\phi\rightarrow M_1}\|Q(t)\phi-Q(t)M_1\|=0$, $\forall t\in[0, \omega]$, 则存在$\eta_1>0$使得对任意的$\phi\in X_0$, $\|\phi-M_1\|<\eta_1$, 得$\|Q(t)\phi-Q(t)M_1\|<\varepsilon$, $t\in[0, \omega]$.

结论3  对所有的$\phi\in X_0$, $\limsup\limits_{n\to\infty}\|Q(n\omega)\phi-M_1\|\geq\eta_1$.

反证法.假设存在某个$\psi\in X_0$, 使得$\limsup\limits_{n\to\infty}\|Q(n\omega)\psi-M_1\|<\eta_1$.则存在一个整数$N_1\geq1$, 使得对所有的$n\geq N_1$有$\|Q(n\omega)\psi-M_1\|<\eta_1$.当$t\geq N_1\omega$时, 得$t=n\omega+t_1$, $n\geq N_1$, $t_1\in[0, \omega)$, $\|Q(t)\psi-Q(t)M_1\|=\|Q(t_1)Q(n\omega)\psi-Q(t_1)Q(n\omega)M_1\| =\|Q(t_1)Q(n\omega)\psi-Q(t_1)M_1\|<\varepsilon$.则当$t\geq N_1\omega$时, 有$0\leq S(t)<\varepsilon$, $0\leq E(t)<\varepsilon$, $0<I(t)<\varepsilon$, $0<B(t)<\varepsilon$, $0<P(t)<\varepsilon$, $0<N(t)<3\varepsilon$, 因此$\lim\limits_{t\rightarrow \infty}(N(t)-S^*(t))=0$, 矛盾.

因为$\lim\limits_{\phi\rightarrow M_2}\|Q(t)\phi-Q(t)M_2\|=0$, $\forall t\in[0, \omega]$, 则对任意的$0<\epsilon<\min\limits_{t\in[0, \omega]}\{S^*(t)\}$, 存在$\eta_2>0$使得对任意的$\phi\in X_0$, $\|\phi-M_2\|<\eta_2$, 得$\|Q(t)\phi-Q(t)M_2\|<\epsilon$, $\forall t\in[0, \omega]$.

结论4  对任意的$\phi\in X_0$, $\limsup\limits_{n\to\infty}\|Q(n\omega)\phi-M_2\|\geq\eta_2$.

反证法.假设存在某个$\psi\in X_0$使得$\limsup\limits_{n\to\infty}\|Q(n\omega)\psi-M_2\|<\eta_2$.则存在$N_2\geq 1$, 使得当$n\geq N_2$时有$\|Q(n\omega)\psi-M_2\|<\eta_2$.对任意的$t\geq N_2\omega$, 得$t=n\omega+t_2$, $n\geq N_2$, $t_2\in[0, \omega)$, $\|Q(t)\psi-Q(t)M_2\|=\|Q(t_2)Q(n\omega)\psi-Q(t_2)Q(n\omega)M_2\| =\|Q(t_2)Q(n\omega)\psi-Q(t_2)M_2\|<\epsilon$.因此, $S(t)>S^*(t)-\epsilon$, $0\leq E(t)<\epsilon$, $0<I(t)<\epsilon$, $0<B(t)<\epsilon$, $0<P(t)<\epsilon$, $\forall t\geq N_2\omega$.考虑如下线性系统

令$\hat{P}_\epsilon(t)$为系统(3.3)的解映射, $\hat{P}_\epsilon:=\hat{P}_\epsilon(\omega)$为相应的庞加莱映射.则$\lim\limits_{\epsilon\rightarrow0^+}r(\hat{P}_\epsilon)=r(P)>1$.固定充分小的$\epsilon>0$, 使得$r(\hat{P}_\epsilon)>1$.类似于对系统(2.5)的分析, 可以证明当$t>2\tau$时$\hat{P}_\epsilon(t)$为紧的和强单调的.则由引理2.5知, 存在正的$\omega$周期函数$\hat{v}^*(t)=(\hat{v}^*_1(t), \hat{v}^*_2(t))$使得$w^*_\epsilon(t)=e^{\frac{\ln r(\hat{P}_\epsilon)}{\omega}t}\hat{v}^*(t)$为系统(3.3)的正解.显然$\lim\limits_{t\rightarrow \infty}w_\epsilon^*(t)=\infty$.当$t\geq N_2\omega+\tau$时得

因为$I(t, \psi)>0$, $B(t, \psi)>0$, $P(t, \psi)>0$, $\forall t\geq0$, 选择充分小的$L>0$使得

由文献[13]中定理5.1.1可得

因此$\lim\limits_{t\rightarrow \infty}I(t, \psi)=\infty$, $\lim\limits_{t\rightarrow \infty}B(t, \psi)=\infty$, $\lim\limits_{t\rightarrow \infty}P(t, \psi)=\infty$, 矛盾.

定义

对任意给定的$\psi\in \partial X_0$得$\psi_3(0)=0$或者$\psi_4(0)=0$或者$\psi_5(0)=0$.

如果$\psi_3(0)=0$, 分以下两种情况进行考虑.

情形1  对任意的$t\geq0$, $I(t, \psi)=0$.

由系统(2.1)的第三个方程得, $S(t-\tau, \psi)B(t-\tau, \psi)=0$, $\forall t\geq \tau$.因此由方程(2.3)得$E(t, \psi)=0$, $\forall t\geq \tau$.根据系统(2.1)的第四和第五个方程知, 当$t\rightarrow \infty$时, $B(t, \psi)\rightarrow0$, $P(t, \psi)\rightarrow0$.由系统(2.1)的第一个方程知当$t\rightarrow \infty$时, $S(t, \psi)\rightarrow 0$或者$S(t, \psi)-S^*(t, \psi)\rightarrow 0$.在这种情况下, 当$n\rightarrow \infty$时, $Q^n(\psi)\rightarrow M_1$或者$Q^n(\psi)\rightarrow M_2$.

情形2  存在某个$t_3>0$, 使得$I(t_3, \psi)>0$.

由系统(2.1)的第三个方程得$I(t, \psi)>0$, $\forall t\geq t_3$.则由系统(2.1)中的第四和第五个方程知$B(t, \psi)>0$, $P(t, \psi)>0$, $\forall t\geq t_3$.因此当$n\omega>t_3$时, $Q^n(\psi)\in X_0$.

对于$\psi_4(0)=0$或者$\psi_5(0)=0$的情况, 可以做类似的分析.最终可知对任意给定的$\psi\in M_\partial$, 当$n\rightarrow \infty$时, $Q^n(\psi)\rightarrow M_1$或者$Q^n(\psi)\rightarrow M_2$.因此

$\{M_1, M_2\}$的任意子集在$\partial X_0$上不能形成一个循环.由结论3和4知$M_1$和$M_2$为$X$上的孤立的不变集, 且$W^s(M_i)\cap X_0=\emptyset$, $i=1, 2$, 这里$W^s(M_i)$为$M_i$的稳定流形.由文献[18]中定理1.3.1和注1.3.1知$Q: X\rightarrow X$关于$X_0$是一致持续的.因此, 由文献[18]中定理3.1.1知周期半流$Q(t): X\rightarrow X$关于$X_0$也是一致持续的.由文献[19]中定理4.5知系统(2.1)有一个$\omega$周期解$Q(t)\phi^*$, $\phi^* \in X_0$.则$S(t, \phi^*)\geq0$, $E(t, \phi^*)\geq0$, $I(t, \phi^*)>0$, $B(t, \phi^*)>0$, $P(t, \phi^*)>0$.下证存在$\tilde{t}>0$使得$S(\tilde{t}, \phi^*)>0$, 否则由$S(t, \phi^*)$的周期性得$S(t, \phi^*)\equiv0$, $\forall t\geq0$.由系统(2.1)的第一式得$E(t, \phi^*)=I(t, \phi^*)=0$, 矛盾.易证对于任意的$t\geq \tilde{t}$, $S(t, \phi^*)>0$.由$S(t, \phi^*)$的周期性得$S(t, \phi^*)>0$, $\forall t\geq0$.由系统(2.3)得$E(t, \phi^*)>0$, $\forall t\geq0$.因此, $(S(t, \phi^*), E(t, \phi^*), I(t, \phi^*), B(t, \phi^*), P(t, \phi^*))$是系统(2.1)的一个正的$\omega$周期解.

由文献[19]中定理4.5, 定义$\rho(x)=d(x, \partial X_0)$, 则$Q: X_0\rightarrow X_0$有一个紧的全局吸引子$A_0$.对任意的$\phi\in A_0$得$\phi_i(0)>0$, $i=3, 4, 5$.令

则$\forall\psi\in B_0$, $\psi_i(0)>0$, $i=3, 4, 5$.易知$\forall\phi\in X_0$, $\lim\limits_{t\rightarrow \infty}d(Q(t)\phi, B_0)=0$.定义连续的函数$p: {\cal X}\rightarrow {{\Bbb R}} _{+}$为

显然, $\forall\phi\in B_0$, $p(\phi)>0$.因为$B_0$为$X_0$的一个紧子集, 则${ }\inf\limits_{\phi\in B_0}p(\phi)=\min\limits_{\phi\in B_0}p(\phi)>0$.因此存在$\xi>0$使得

证毕.

本节将研究系统(2.1)对应的自治系统, 即假设系统(2.1)中的所有参数为正常数, 时滞$\tau$为非负常数.此时系统(2.1)变为

对于系统(4.1), 假设$({\rm H1})$变为:

($\rm H2$) $r>\mu.$

显然系统(4.1)有一个灭绝平衡点$Q_0=(0, 0, 0, 0, 0)$, 一个无病平衡点$Q_1=(\frac{r-\mu}{b\mu}, 0, 0, 0, 0)$.由文献[14]中推论2.1知系统(4.1)的基本再生数为

系统(4.1)的正平衡点为$Q^*=(S^*, E^*, I^*, B^*, P^*)$, $S^*=\frac{k\delta e^{\mu\tau}}{\beta \eta}$, $E^*=\frac{(e^{\mu\tau}-1)(\mu+\alpha)I^*}{\mu}$, $B^*=\frac{\eta(\mu+\alpha)I^*}{k\delta}$, $P^*=\frac{(\mu+\alpha)I^*}{k}$, $I^*$为下面方程的正根

其中$A_0=\alpha bd+\mu bd^2$, $A_1=\alpha bS^*+\alpha+(\mu-r)d+2\mu bdS^*$, $A_2=\mu b(S^*)^2(1-[{R}_0])$, $d=\frac{(e^{\mu\tau}-1)(\mu+\alpha)}{\mu}+1.$如果$[R_0]\leq 1$, 则$A_2\geq0$, $A_1>(\mu-r)d+\mu bdS^*=\frac{A}{S^*}\geq 0$, 因此方程(4.2)没有正根.如果$[R_0]>1$, 则$A_2<0$, 方程(4.2)有唯一的正根

因此当且仅当$[R_0]>1$时, $Q^*$存在.

定义

易得在$Q_0$处的特征方程为

因为方程(4.3)有一个正根$r-\mu$, 则$Q_0$是不稳定的.

对于无病平衡点$Q_1$, 它的特征方程有两个负的特征根$-\mu$和$(\frac{\mu}{r}-1)\mu$, 其他特征根为下面方程的根

这里$a_1=k+\mu+\alpha+\delta$, $a_2=k(\mu+\alpha+\delta)+\delta(\mu+\alpha)$, $a_3=k\delta(\mu+\alpha)$, $a_4=\frac{\beta\eta(r-\mu)(\mu+\alpha)}{b\mu}$, 显然$a_i>0$, $i=1, 2, 3, 4.$

如果$[R_0]>1$时, $g(0, \tau)=a_3-a_4e^{-\mu\tau}=k\delta(\mu+\alpha)(1-[R_0])<0$, $\lim\limits_{z\rightarrow +\infty}g(z, \tau)\rightarrow +\infty$.则$g(z, \tau)=0$存在正根, 因此$Q_1$不稳定.

当$[R_0]<1$时, 如果$\tau=0$, 则方程(4.4)具有如下形式

因为$a_3-a_4>0$, $a_1a_2-(a_3-a_4)>a_1a_2-a_3>(\mu+\alpha)k(\mu+\alpha+\delta)-k\delta(\mu+\alpha) =k(\mu+\alpha)^2>0$, 则$Q_1$局部渐近稳定.下面证明如果$[R_0]<1$, 则对任意的$\tau\geq0$, 方程(4.4)没有纯虚根.令$z=iv$, $v\in {{\Bbb R}}$是方程(4.4)的根, 则有

其中$b_1=k^2+\delta^2+(\mu+\alpha)^2$, $b_2=k^2[\delta^2+(\mu+\alpha)^2]+\delta^2(\mu+\alpha)^2$, $b_3=a_3(a_3+a_4e^{-\mu\tau})(1-[R_0])$, 因为$b_i>0$, $i=1, 2, 3$, 则方程(4.6)没有实根.因此, $\forall\tau\geq0$, $Q_1$局部渐近稳定.结合定理3.1得到下面的定理.

定理4.1  如果$[R_0]\leq 1$, 则系统(4.1)仅存在灭绝平衡点$Q_0=(0, 0, 0, 0, 0)$和无病平衡点$Q_1=(\frac{r-\mu}{b\mu}, 0, 0, 0, 0)$, 且$Q_0$总是不稳定的, 当$[R_0]<1$时$Q_1$在$\Omega\setminus(\{(0, 0, 0)\}\times C([-\tau, 0], {{\Bbb R}} _{+})\times{{\Bbb R}} _{+})$内全局渐近稳定.当$[{R}_0]>1$时, $Q_1$不稳定, 系统(4.1)存在唯一的正平衡点$Q^*=(S^*, E^*, I^*, B^*, P^*)$.

现在来分析正平衡点$Q^*=(S^*, E^*, I^*, B^*, P^*)$的稳定性.为了分析的可行性, 令$\alpha=0$.记$\theta_1=\mu+\beta B^*$, $\theta_2=k+\delta+\mu$, $\theta_3=k(\delta+\mu)+\delta\mu$, 则在$Q^*=(S^*, E^*, I^*, B^*, P^*)$处的特征方程为

这里

其中$c_1=\theta_1+\theta_2,$$c_2=\theta_1\theta_2+\theta_3,$$c_3=\theta_1\theta_3+k\delta\mu,$$c_4=k\delta\mu\theta_1,$$c_5=\beta S^*\eta\mu.$特征方程(4.7)有一个负根$-\mu\left(1-\frac{\mu}{r}\right)$, 其余特征根由多项式$F(\lambda, \tau)$来决定.

当$\tau=0$时, 得

直接计算得$c_3-c_5=\theta_1\theta_3>0$, $c_4-c_5\mu=k\delta\mu\beta B^*>0$, $c_1c_2-(c_3-c_5)= \theta_1\theta_2(\theta_1+\theta_2)+\theta_2\theta_3>0$, $(c_3-c_5)[c_1c_2-(c_3-c_5)]-(c_3-c_5\mu)c^2_1 =\mu^2\theta_1\theta_2[\theta_3+\beta B^*(k+\delta)]+\theta^2_1\beta B^*(\mu+\delta)(k^2+\theta_3) +\theta^2_2\mu^2[\theta_3+2\beta B^*(k+\delta)]+\theta_2\beta B^*[\beta B^*(\mu+\delta)(k^2+\theta_3)+k\delta\mu(k+\delta)] +\theta_1\theta_2\theta^2_3>0$.因此$F(\lambda, 0)=0$所有的根均具有负的实部.

令$\lambda={\rm i}\upsilon$, $\upsilon\in {{\Bbb R}}$为$F(\lambda, \tau)=0$的根, 得

其中$e_1=\theta^2_1+k^2+\delta^2+\mu^2>0$, $e_2=\theta^2_1(k^2+\delta^2+\mu^2)+k^2(\delta^2+\mu^2)+\delta^2\mu^2>0$, $e_3=\theta^2_1[k^2(\delta^2+\mu^2)+\delta^2\mu^2]>0$, $e_4=k^2\delta^2\mu^2\beta B^*(\theta_1+\mu)>0$, 因此$F(\lambda, \tau)=0$没有纯虚根.则$\forall\tau\geq0$, $Q^*$局部渐近稳定.

定理4.2  如果$[R_0]>1$, $\alpha=0$.则系统(4.1)有唯一的正平衡点$Q^*=(S^*, E^*, I^*, B^*, P^*)$, 且它是局部渐近稳定的.

利用波动方法^[20], 可以得到$Q^*$的全局渐近稳定性结果.

定理4.3  令$\alpha=0$.如果$[R_0]>1$, 则对任意的初值$\phi\in \Omega$, $\phi_i(0)>0$, $i=3, 4, 5$, 有$\lim\limits_{t\rightarrow \infty}u(t, \phi)=Q^*$, 因此正平衡点$Q^*=(S^*, E^*, I^*, B^*, P^*)$全局渐近稳定.

证  记$S^\infty=\limsup\limits_{t\rightarrow \infty}S(t),$${ } S_\infty=\liminf\limits_{t\rightarrow \infty} S(t).$类似地定义$E^\infty$, $E_\infty$, $I^\infty$, $I_\infty$, $B^\infty$, $B_\infty$, $P^\infty$, $P_\infty$.

动物的总人口$N(t)$满足下面的微分方程

因为$N(0)=S(0)+E(0)+I(0)>0$, 则$\lim\limits_{t\rightarrow \infty}N(t)=\Theta$全局渐近稳定, 这里$\Theta=\frac{r-\mu}{b\mu}$.由于系统(4.1)中的第二个方程不在其他方程中出现, 因此考虑下面的极限方程

令$h(t)=S(t)+e^{\mu\tau}I(t+\tau)$, 得

则$\lim\limits_{t\rightarrow \infty}h(t)=\Theta$全局渐近稳定.进一步考虑如下的极限方程

根据引理2.1的证明可知

是系统(4.12)的正向不变集.与定理3.2的证明类似, 得系统(4.12)是一致持续的, 即存在$\zeta>0$, 对于任意给定的$\psi=(\psi_1, \psi_2, \psi_3)\in {\cal D}$, $\psi_i(0)>0$, $i=1, 2, 3$, 系统(4.12)的解$(\bar{I}(t, \psi), \bar{B}(t, \psi), \bar{P}(t, \psi))$满足

对任意的$\psi\in {\cal D}$, $\psi_i(0)>0$, $i=1, 2, 3$, 记$(\bar{I}(t), \bar{B}(t), \bar{P}(t))=(\bar{I}(t, \psi), \bar{B}(t, \psi), \bar{P}(t, \psi))$.显然$\Theta e^{-\mu\tau}\geq\bar{I}^\infty\geq \bar{I}_\infty\geq \zeta$, $\bar{B}^\infty\geq \bar{B}_\infty\geq \zeta$, $\bar{P}^\infty\geq \bar{P}_\infty\geq\zeta$.因此存在序列$t^i_n$和$\sigma^i_n$, $i=1, 2, 3$, 使得

由系统(4.12)的第一个方程得

由此得

类似地, 由系统(4.12)的第二个和第三个方程得

结合(4.13), (4.14)和(4.15)式, 得

因此, $\bar{I}_\infty\geq I^*=\frac{k\delta}{\beta\eta}([R_0]-1)\geq\bar{I}^\infty$, 则$\bar{I}^\infty=\bar{I}_\infty$.由(4.14)和(4.15)式, 得$\bar{B}^\infty=\bar{B}_\infty$, $\bar{P}^\infty=\bar{P}_\infty$.因此对任意的$\psi\in {\cal D}$, $\psi_i(0)>0$, $i=1, 2, 3$, $\lim\limits_{t\rightarrow \infty}(\bar{I}(t), \bar{B}(t), \bar{P}(t))=(I^*, B^*, P^*)$.根据链传递集理论(见文献[18], 引理1.2.2和定理1.2.1, 1.3.1), 由系统(4.12)解的全局吸引性可以得到系统(4.1)的解的全局吸引性.因此对任意的$\psi\in {\cal D}$, $\psi_i(0)>0$, $i=1, 2, 3$, 得$\lim\limits_{t\rightarrow \infty} u(t, \phi)=Q^*$.结合定理4.2知, 对任意的$\phi\in \Omega$, $\phi_i(0)>0$, $i=3, 4, 5$, 如果$[R_0]>1$, 则$Q^*$全局渐近稳定.证毕.

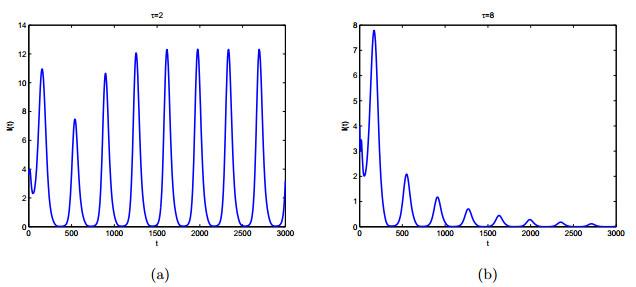
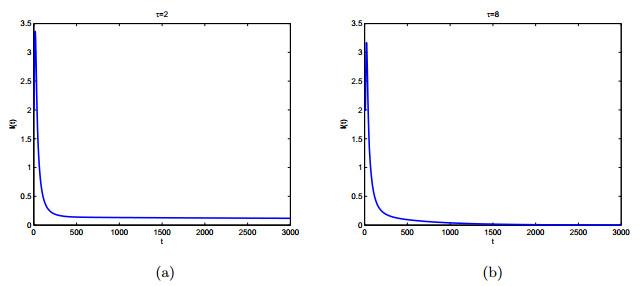
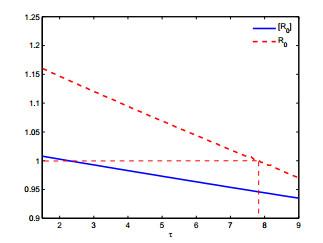
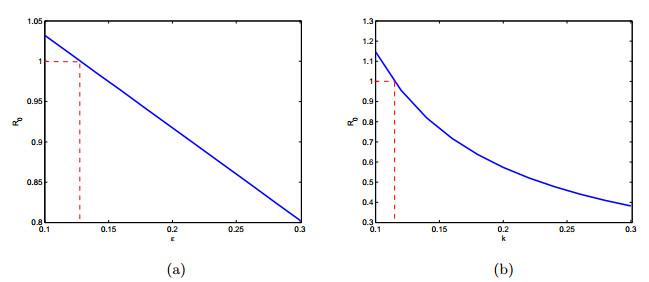
本节通过数值拟合来研究潜伏期和季节性对炭疽传播的影响.参数单位为天, 取$r=0.94$/天, $b=0.2$, $\mu=0.01$/天, $k=0.1$/天, $\delta=0.1$/天.取$\beta(t)=0.011(1+0.8\sin({\pi t\over180}))$/天/克孢子, $\alpha(t)=\frac{1}{7}(1+0.8\sin({\pi t\over180}))$/天, $\eta(t)=0.002(1+0.8\sin({\pi t\over180}))$克孢子/尸体/天.由于潜伏期随着宿主不同而有所变化, 在牛身体内潜伏期为1到14天^[21], 因此令$\tau=2$.

根据文献[22]中的引理2.5和注3.2, 可以数值计算基本再生数$R_0$.根据以上参数的值得$R_0=1.1466>1$, 则疾病在动物种群内持续存在(见图 1(a)).如果增加潜伏期到$\tau=8$, 计算得$R_0=0.997<1$, 因此炭疽灭绝(见图 1(b)).这些结果与定理3.1和3.2一致.对自治系统(4.1), 染病者随时间的变化见图 2.当$\tau=2$时, 得$[R_{0}]=1.0027$, 此时解最终收敛到正平衡点.如果$\tau=8$, 得$[R_{0}]=0.9443$, 解最终趋向于无病平衡点, 意味着疾病最终灭绝.同时图 1和2表明自治系统可能低估了炭疽疾病的危险性.

下面研究基本再生数关于参数的敏感性.令潜伏期$\tau$在区间[1.5, 9]上变化, 其他参数与图 1中一样.基本再生数关于潜伏期的曲线如图 3所示.在图 3中有两条曲线, 红色曲线为周期模型(2.1)的基本再生数关于潜伏期的图形, 蓝色曲线为自治系统(4.1)的基本再生数关于潜伏期的图形.由图 3知蓝色曲线总是位于红色曲线的下方, 这表明自治系统过低估计了炭疽疾病的危险性. $R_0$关于潜伏期是单调递减的.因此可以通过药物或者控制措施延长炭疽的潜伏期来减少炭疽传染的危害.为了根除炭疽疾病, 应该使得潜伏期$\tau>7.8$.

对动物进行接种是可能的, 为了研究接种的效果, 用$(1-\varepsilon)\beta(t)$代替$\beta(t)$, 其中$\varepsilon\in (0, 1)$代表接种成功的比例. 图 4(a)表明$R_0$为$\varepsilon$的单减函数.为了根除疾病, 成功接种比例应该大于0.127, 对易感者进行接种, 减少疾病传染率是一个非常有效的控制疾病的方法.人们也可以通过移除动物尸体减少动物与空气中孢子的接触.令参数$k$在区间[0.1, 0.3]上变化, 由图 4(b)知如果$k>0.115$, 则炭疽可以根除.

由于炭疽爆发的季节性, 本文建立了一个周期和时滞的炭疽模型.利用文献[14]得到了模型的基本再生数$R_0$, 建立了阈值理论, 证明了当$R_0<1$时疾病根除, 当$R_0>1$时疾病持久.对相应的自治模型得到了基本再生数的明确表达式, 利用波动方法证明了正平衡点的全局渐近稳定性.数值拟合表明忽略季节性可能会低估疾病传染的危险.炭疽季节性的爆发对疾病控制带来了挑战.潜伏期越大, 基本再生数越小, 因此可以通过延长潜伏期来减缓疾病的传播.同时研究发现通过对易感者动物接种或者移除动物尸体都可以使得炭疽疾病灭绝.但是在实际中, 如何选择接种和移除尸体使得对炭疽的控制达到最优是一个很困难的问题, 需要进一步的讨论^[7], 接种与移除尸体的选择将受到各自所涉及的成本的影响.特别是针对野生动物, 这些措施的实施非常复杂, 而且成本相当昂贵.

在我们的模型中, 忽略了媒介种群的影响, 但事实已经证明, 苍蝇可能在炭疽爆发中发挥了重要的作用^[23].食腐动物对炭疽传播的影响也需要进一步进行研究.炭疽对人和动物都有影响, 因此考虑同时具有人和动物的炭疽模型更加合理.人类迁徙很常见, 可能对炭疽传播有很大的影响.这些问题我们留待进一步研究.