1 引言
自变量分段连续微分方程广泛存在于各个领域, 是数学分支中一类重要的模型, 它能将某些连续和离散变量混合系统问题有效地解决, 如反馈控制[8].同时可以通过研究微分方程和差分方程的性质, 将复杂的物理和生命科学等问题用简单的数学模型进行近似, 很大程度促进了其理论和相关算法的进一步研究, 此类方程有特别重要的理论价值和现实意义[9-13].目前有关其解析解振动性的理论已经比较成熟, 然而近年来才对其数值解振动性进行讨论和研究, 同时有关数值振动性的研究目前仅局限于1维情形, 本论文把相关结论推广到2维情形, 更好地对实际问题进行分析和处理.文献[14-24]介绍了自变量分段连续延迟微分方程的理论.下面给出振动和非振动的定义.
定义1.1[25] 设
2 解析解的振动性分析
考虑下列自变量分段连续系统
其中
注2.1
令
定义2.1[25] 方程(2.1)的解是指定义在区间
下面的定理给出了方程(2.1)的解.
定理2.1[25] 对于任意给定的
其中
方程(2.2)的特征方程是
定理2.2[25] 下列陈述是等价的:
定理2.3 方程(2.1)的每个解振动当且仅当满足下列条件
方程(2.1)存在一个非振动解当且仅当满足下列条件
证 由定理
的根
由于特征方程(2.3)有实根, 则有
即
接下来考虑根的情况, 当
即
或
即
当
即
或
即
结合判别式的情况可得
由于方程的每个解振动等价于方程没有一个非振动解, 由方程存在一个非振动解的充要条件, 我们可以得到方程每个解振动的条件为
定理2.3得证.
3 数值解的振动性分析
与文献[26]类似, 线性
其中
其中
由方程(3.1)有
为了讨论和叙述的方便, 我们引入以下记号:
方程(3.2)的特征方程是
下面的定理给出了
定理3.1
(1)
(2)
证 容易得到
同理可得
因此, 如果
且
故
通过定理
定理3.2 方程(3.2)和方程(3.3)分别给出了
为了研究方程(3.3)的振动性, 只需研究方程(3.2)的振动性.令
其中
引理3.1 方程(3.2)存在一个非振动解当且仅当
证 根据文献[25], 方程(3.2)存在一个非振动解的充分必要条件是其特征方程(3.4)
的根
由于特征方程(3.4)存在实根, 则有
即
接下来考虑根的情况, 当
即
或
即
当
即
或
即
结合判别式的条件可得
因此方程(3.2)存在一个非振动解当且仅当
根据定理
推论3.1
4 方程振动性的保持性
根据定理
定理4.1
下面的引理给出了
引理4.1
(Ⅱ)如果满足下列条件之一:
则
证 (Ⅰ)
同理可得
(Ⅱ)
或者
令
则
当
可得
则有
只需证
由
又
即
结论得证.
则有
只需证
由
又
即
结论得证.
则有
只需证
由
又
即
结论得证.
可得
则有
只需证
即
由
又
即
结论得证.
引理4.2[26] 对任意的
其中
根据定理
定理4.2
其中
5 数值算例
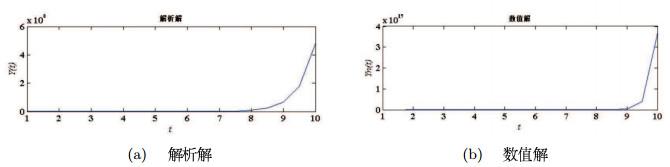
例1 考虑以下方程
其中
图 1
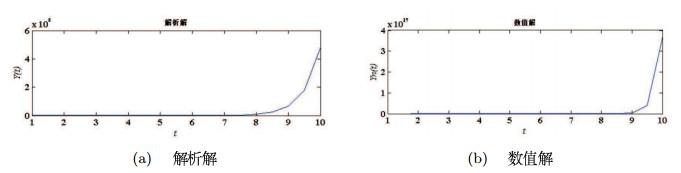
例2 考虑方程
图 2
参考文献
Retarded differential equations with piecewise constant delays
DOI:10.1016/0022-247X(84)90248-8 [本文引用: 1]
Numerical stability and oscillation of the Runge-Kutta methods for equation
Oscillatory and asymptotic behaviour of odd order delay differential equations with impluses
Estimates on the dimension of an exponential attractor for a delay differential equation
A sharp oscillation criterion for a linear delay differential equation
A sharp oscillation result for second-order half-linear noncanonical delay differential equations
On oscillatory second order differential equations with variable delays
Linear optimal control problems with piecewisw analytic solutions
DOI:10.1006/jmaa.1996.0016 [本文引用: 1]
Advanced differential equations with piecewise constant argument deviations
DOI:10.1155/S0161171283000599 [本文引用: 1]
Stability of
DOI:10.1016/j.camwa.2005.02.002
On the reduction principle for differential equations with piecewise constant argument of generalized type
DOI:10.1016/j.jmaa.2007.03.010
Stability analysis of a population model with piecewisw constant arguments
DOI:10.1016/j.nonrwa.2010.10.011
Numerical oscillation and non-oscillation for differential equation with piecewise continuous arguments of mixed type
Oscillations in systems of differential equations with piecewise constant argument
DOI:10.1016/0022-247X(89)90286-2 [本文引用: 1]
New results on oscillation for delay differential equations with piecewise constant argument
DOI:10.1016/S0898-1221(03)90005-8
Stability and oscillations of numerical solutions for differential equations with piecewise continuous arguments of alternately advanced and retarded type
Oscillation of fourth order delay differential equations
A note on oscillation of second-order delay differential equations
Oscillation criteria for odd-order nonlinear delay differential equations with a middle term
DOI:10.1002/mma.4377
Third-order neutral delay differential equations: New iterative criteria for oscillation
Oscillation analysis of numerical solution in the
Preservation of oscillation of the Runge-Kutta method for equation
DOI:10.1016/j.camwa.2009.07.030
Oscillation analysis of numerical solutions in the
DOI:10.1002/mma.3458
Preservation of oscillation in the Runge-Kutta method for a type of advanced differential equation
DOI:10.1080/01630563.2015.1070863 [本文引用: 1]
Stability of
DOI:10.1016/j.camwa.2005.02.002 [本文引用: 2]