一类自变量分段连续系统的振动性分析

摘要/Abstract

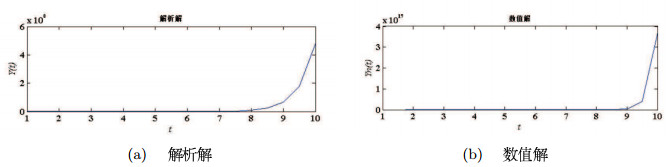
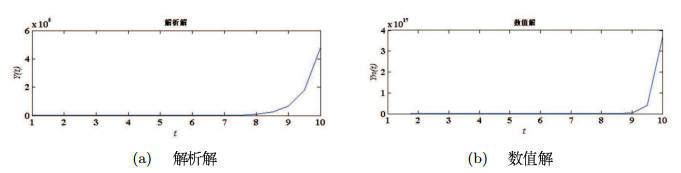
摘要：

该文主要运用 $\theta$ -方法对一类滞后型自变量分段连续系统的振动性进行分析，讨论了解析解和数值解的振动性和非振动性，得到了数值方法在解析解振动条件下保持方程振动性的充分条件，并给出了数值算例.

关键词: 自变量分段连续, 延迟微分系统, 数值解, 振动性, θ -方法

Abstract:

In this paper, we mainly use $\theta$ -method to analyze the oscillation of differential equations with piecewise continuous arguments of retarded type, and discuss the oscillation and non-oscillation of analytic solution and numerical solution. The sufficient conditions for the numerical methods to preserve the oscillation of the equation under the condition of the analytic solution oscillation are obtained. Meanwhile, some numerical experiments are given.

Key words: Piecewise continuous arguments, Delay differential system, Numerical solutions, Oscillation, θ-methods

中图分类号:

O241.8

刘莹,高建芳. 一类自变量分段连续系统的振动性分析[J]. 数学物理学报, 2022, 42(3): 826-838.

Ying Liu,Jianfang Gao. Oscillation Analysis of a Kind of Systems with Piecewise Continuous Arguments[J]. Acta mathematica scientia,Series A, 2022, 42(3): 826-838.

图/表 2

参考文献 26

1	Cooke K L , Wiener J . Retarded differential equations with piecewise constant delays. J Math Anal Appl, 1984, 99, 265- 297 doi: 10.1016/0022-247X(84)90248-8
2	Song M H , Liu M Z . Numerical stability and oscillation of the Runge-Kutta methods for equation $x'(t)=ax(t)+a_{0}x(M[\frac{t+N}{M}])$ . Adv Difference Equa, 2012, 146, 1- 13
3	Chen F . Oscillatory and asymptotic behaviour of odd order delay differential equations with impluses. J Math Sci, 2013, 15, 258- 273
4	Habibi S . Estimates on the dimension of an exponential attractor for a delay differential equation. Math Slovaca, 2014, 64, 1237- 1248 doi: 10.2478/s12175-014-0272-0
5	Á Garab , Pituk M , Stavroulakis I P . A sharp oscillation criterion for a linear delay differential equation. Appl Math Lett, 2019, 93, 58- 65 doi: 10.1016/j.aml.2019.01.042
6	Durina J , Jadlovská I . A sharp oscillation result for second-order half-linear noncanonical delay differential equations. Electron J Qual Theory Differ Equa, 2020, 2020 (46): 1- 14
7	Sethi A K , Tripathy A K . On oscillatory second order differential equations with variable delays. Palestine J Math, 2021, 3 (1): 11- 24
8	Pullan M C . Linear optimal control problems with piecewisw analytic solutions. J Math Anal Appl, 1996, 197, 207- 226 doi: 10.1006/jmaa.1996.0016
9	Shah S M , Wiener J . Advanced differential equations with piecewise constant argument deviations. Int J Math Sci, 1983, 6, 671- 703 doi: 10.1155/S0161171283000599
10	Song M H , Yang Z W , Liu M Z . Stability of $\theta$ -methods for advanced differential equations with piecewise continuous arguments. Comput Math Appl, 2005, 49, 1295- 1301 doi: 10.1016/j.camwa.2005.02.002
11	Akhmet M U . On the reduction principle for differential equations with piecewise constant argument of generalized type. J Math Anal Appl, 2007, 336, 646- 663 doi: 10.1016/j.jmaa.2007.03.010
12	Ozturk I , Bozkurt F . Stability analysis of a population model with piecewisw constant arguments. Nonlinear Anal Real World Appl, 2011, 12, 1532- 1545 doi: 10.1016/j.nonrwa.2010.10.011
13	Gao J F . Numerical oscillation and non-oscillation for differential equation with piecewise continuous arguments of mixed type. Appl Math Comput, 2017, 299, 16- 27
14	Wiener J , Cooke K L . Oscillations in systems of differential equations with piecewise constant argument. J Math Anal Appl, 1989, 137, 221- 239 doi: 10.1016/0022-247X(89)90286-2
15	Luo Z G , Shen J H . New results on oscillation for delay differential equations with piecewise constant argument. Comput Math Appl, 2003, 45, 1841- 1848 doi: 10.1016/S0898-1221(03)90005-8
16	Wang Q , Zhu Q Y , Liu M Z . Stability and oscillations of numerical solutions for differential equations with piecewise continuous arguments of alternately advanced and retarded type. J Comput Appl Math, 2011, 235, 1542- 1552 doi: 10.1016/j.cam.2010.08.041
17	Zhang C , Li T , Saker S H . Oscillation of fourth order delay differential equations. J Math Sci, 2014, 201, 322- 335
18	Džurina J , Jadlovská I . A note on oscillation of second-order delay differential equations. Appl Math Lett, 2017, 69, 126- 132 doi: 10.1016/j.aml.2017.02.003
19	Grace S R , Jadlovská I , Zafer A . Oscillation criteria for odd-order nonlinear delay differential equations with a middle term. Math Methods Appl Sci, 2017, 40, 5147- 5160 doi: 10.1002/mma.4377
20	Moaaz O , Mahmoud E E , Alharbi W R . Third-order neutral delay differential equations: New iterative criteria for oscillation. J Funct Spaces, 2020, 2020 (1): 1- 8
21	Liu M Z , Gao J F , Yang Z W . Oscillation analysis of numerical solution in the $\theta$ -methods for equation $x'(t)+ax(t)+a_1x([t-1])=0$ . Appl Math Comput, 2007, 186, 566- 578
22	Liu M Z , Gao J F , Yang Z W . Preservation of oscillation of the Runge-Kutta method for equation $x'(t)+ax(t)+a_1x([t-1])=0$ . Comput Math Appl, 2009, 58, 1113- 1125 doi: 10.1016/j.camwa.2009.07.030
23	Gao J F , Liu S M . Oscillation analysis of numerical solutions in the $\theta$ -methods for differential equation of advanced type. Math Methods Appl Sci, 2015, 38, 5271- 5278 doi: 10.1002/mma.3458
24	Gao J F , Shi T T , Song F Y . Preservation of oscillation in the Runge-Kutta method for a type of advanced differential equation. Numer Funct Anal Optim, 2015, 36, 1420- 1430 doi: 10.1080/01630563.2015.1070863
25	Györi I , Ladas G . Oscillation Theory of Delay Equations with Applications. Oxford: Clarendon Press, 1991: 32- 197
26	Song M H , Yang Z W , Liu M Z . Stability of $\theta$ -methods for advanced differential equations with piecewise continuous arguments. Comput Math Appl, 2005, 49, 1295- 1301 doi: 10.1016/j.camwa.2005.02.002

Metrics

Viewed

Full text

139

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	0	0	0	139

From	Others	local

Times	1	138
Rate	1%	99%

Abstract

107

Just accepted	Online first	Issue

0	0	107

	From	Others

	Times	107
	Rate	100%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

[1]	张萍,杨甲山,覃桂茳. 时间轴上二阶非线性非自治延迟动力系统的振动性[J]. 数学物理学报, 2022, 42(3): 839-850.
[2]	李文娟,汤获,俞元洪. 具有次线性中立项的二阶阻尼微分方程的振动准则[J]. 数学物理学报, 2022, 42(1): 58-69.
[3]	仉志余,赵成,李宇宇. 时间尺度上带超线性中立项的二阶时滞动力方程的振动性[J]. 数学物理学报, 2021, 41(6): 1838-1852.
[4]	覃桂茳,杨甲山. 具拟线性中立项的二阶变时滞动力方程的振动定理[J]. 数学物理学报, 2021, 41(5): 1492-1503.
[5]	闫朝琳,高建芳. 混合型脉冲微分方程的数值振动性分析[J]. 数学物理学报, 2020, 40(4): 993-1006.
[6]	罗李平,罗振国,曾云辉. 一类非线性脉冲中立抛物型分布参数系统的振动条件[J]. 数学物理学报, 2020, 40(3): 784-795.
[7]	李继猛,杨甲山. 具非线性中立项的二阶延迟微分方程的Philos型准则[J]. 数学物理学报, 2020, 40(1): 169-186.
[8]	张晓建. 具非线性中立项的广义Emden-Fowler微分方程的振动性[J]. 数学物理学报, 2018, 38(4): 728-739.
[9]	罗李平, 罗振国, 邓义华. 脉冲扰动对非线性时滞双曲型分布参数系统振动的影响[J]. 数学物理学报, 2018, 38(2): 313-321.
[10]	李文娟, 汤获, 俞元洪. 中立型Emden-Fowler微分方程的振动性[J]. 数学物理学报, 2017, 37(6): 1062-1069.
[11]	王云竹, 高建芳. 一类非线性延迟微分方程θ-方法的数值解振动分析[J]. 数学物理学报, 2017, 37(2): 342-351.
[12]	杨甲山. 时间测度链上具正负系数的二阶阻尼动力方程的振动准则[J]. 数学物理学报, 2014, 34(2): 393-408.
[13]	殷慰萍. 一类复蒙日－安培方程Dirichlet问题数值解探讨(四)[J]. 数学物理学报, 2013, 33(4): 646-654.
[14]	陈大学. 具有振动系数的二阶非线性中立型时滞动力方程的有界振动性[J]. 数学物理学报, 2013, 33(1): 98-113.
[15]	李同兴, 韩振来, 张承慧, 孙一冰. 时间尺度上三阶Emden-Fowler动力方程的振动准则[J]. 数学物理学报, 2012, 32(1): 222-232.