1 引言
在本文中, 我们考虑以下光滑的无约束优化问题
其中,
其中
对于一个高效的算法来讲, 选择一个合适的线性搜索技术对算法的性能起着至关重要的作用. 目前, 已有许多单调线搜索方法被提出并应用于共轭梯度算法中, 其中Armijo线搜索是最经典、花费最少的方法之一, 它选择集合
其中
但是, 在文献[19-22] 中, 作者指出, 迭代序列
选择初始量
其中,
因为
因为
显然, Zhang-Hager方法[27]中的线性搜索规则可以被视为(1.3)式的一种特殊形式.
其中, 我们称参数
其中,
其中,
实验结果表明, PDY算法的数值性能明显优于经典方法. 然而, 共轭梯度法仍有改进的余地. 为了获得更好的性质和数值性能, 学者们开始将目光转向研究三项共轭梯度法. 他们相信因为其良好的性质, 三项共轭梯度法具有更加优秀的性能, 比如三项共轭梯度法很容易获得充分下降性质. 充分下降性的定义为, 存在一个常数
成立, 充分下降性在共轭梯度算法中有很重要的地位比如它能帮助算法更好的获得全局收敛性也可以使收敛性证明的证明过程更加简单明了. 为了实现这一特性, Zhang等[41]提出了一种三项共轭梯度法, 并将
很明显, Zhang等人提出的方法具有充分的下降性并且很容易建立其收敛性. 然而, 学者们对该算法的数值性能并不满意, 我们是否可以同时获得PRP、HS和LS方法等良好的数值性能以及FR、CD和DY方法等良好的理论证明性能呢?带着这个疑问, Abubaker等[42]提出了一类新的搜索方向, 其搜索方向的迭代方式如下
在这里,
其中的参数定义为
虽然, 搜索方向(1.7)可以获得充分下降性. 但是, 我们能否获得一个性能更加强劲的算法并建立其全局收敛性呢?值得注意的是, 在这个迭代公式中我们仅仅用到了目标函数的梯度信息. 为了提高性能, 新的
本论文的结构如下. 下一节将解释所提出的算法. 第三部分给出了新方法的性质和收敛性结果以及证明. 第四部分给出了"无约束优化问题"和"图像恢复问题"的实验结果. 最后一章将对本文进行总结.
2 创作动机与算法
基于上述思想, 在本节中, 我们将提出了一个新的三项共轭梯度公式, 该公式设计为
其中
以及
目前, 大多数共轭梯度算法的搜索方向并不含有目标函数本身的信息, 而在本文设计的
值得注意的是, 根据
因此
这就说明了
对于共轭参数
通过上述对新的搜索方向的描述, 并结合非单调线性搜索技术, 我们可以得到新的算法步骤如下.
算法一
输入: 参数
输出:
1) 给定一个初始的点
2) while
3) 计算
4) 寻找步长
5) 设
6) 计算
7)
8) end while
9) End
3 性质和收敛性分析
在本节中, 我们将证明新方法的全局收敛性. 首先, 我们需要建立以下假设来研究算法的某些独特性质.
假设
(1) 水平集
(2) 目标函数
其中
注3.1 上述假设意味着存在一个正常数
引理3.1 让搜索方向
证 当
当
所以引理成立. 同时使用Cauchy-Schwartz不等式和(3.2)式, 可以得到
引理3.1证毕.
引理3.2 如果
证 首先使用中值定理, 存在
接下来, 通过(3.5) 和(3.1) 式, 可以得到以下两种情况.
情况1 当
取
情况2 当
存在一个正常数
最后, 设
定理3.1 让
该证明与文献[28]中定理1的证明相同, 因此该证明将不再重复. 同时, 从证明中, 我们可以很容易地得到, 对于每一个
定理3.2 如果假设(2)成立,
证 通过(1.3)和(3.6)式, 很清楚的可以得到
通过(1.3)式, 很明显,
通过
通过上述不等式, 我们完成了证明.
定理3.3 假设(2)成立, 序列
证 根据(1.3), 当
使用(3.6)式, 则可以获得以下不等式
通过(3.5)式, 假设(2)成立以及
结合(3.9)和(3.10)式, 可以得到
由
最后, 设
定理3.4 如果假设(1)(2)成立, 并且序列
证 我们将使用反证法的思想, 存在一个常数
通过(3.3)式得到
再使用(2.1), (2.3), (2.4), (3.3), (3.4)式和Cauchy-Schwartz不等式可以得到
当
当
设
通过(3.8)式, 使用(3.13)式, 则有
这就与(3.7)式产生了矛盾, 所以(3.11)式是成立的. 定理3.4证毕.
4 数值实验
在这一章节中, 我们设计了两个实验来研究算法的性能, 并将所提出的算法与其他几种经典的算法进行计算效率和性能的比较. 这两个实验分别是无约束优化问题和图像恢复问题, 在之后的小节中会详细的介绍这两个实验和实验的结果分析. 接下来我们先将列出一些关于实验的信息和参数.
使用的数学软件: MATLAB R2017a.
算法运行环境: Intel(R) Core (TM) i7-4710MQ CPU @ 2.50 GHz, 8.0 GB, RAM, 以及Windows 10操作系统.
实验中使用的方法以及图例曲线解释如下.
方法1 (M1): NHSDY方法(算法一).
方法2 (M2): 一种PDY类型的方法[40].
方法3 (M3): 一种在Wolfe-Powell(WP)线性搜索技术下的PRP方法.
方法4 (M4): 一个结合了"HSDY"方法(1.7)和线性搜索技术(1.3)的方法.
方法5 (M5): 一个结合了(2.1)式和标准Armijo线性搜索技术(1.2)的方法
4.1 无约束优化问题
为了验证NHSDY方法(方法1)的数值性能, 我们通过使用不同的方法解决无约束优化问题来进行对比, 本文测试了算法的迭代次数(NI)、计算函数的次数和其梯度次数之和(NFG)以及算法的CPU时间(CPU). 同时, 在本数值实验中的三个实验对照组分别是: 方法2、方法3和方法4. 实验中使用的参数数据如下.
被测试问题的维度 3000维, 9000维以及15000维.
使用到的参数 所有的算法都在参数
停止准则(Himmelblau停止准则[44]) 对于所有的算法, 如果满足条件
被测试问题 本实验测试了74个无约束优化问题, 详细的问题列表可以见Andrei的著作[12].
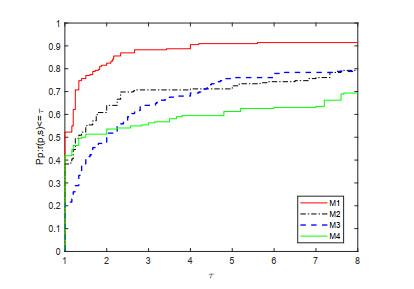
在Dolan和Moré发表的论文[45]中, 提出了一种分析和比较这些算法效率的方法. 在本文中将使用这种方法对四种不同的算法进行比较. 图中水平和垂直坐标的参数表示如下:
图 1
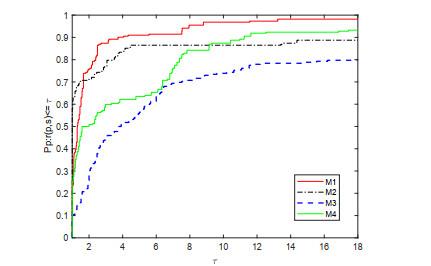
图 2
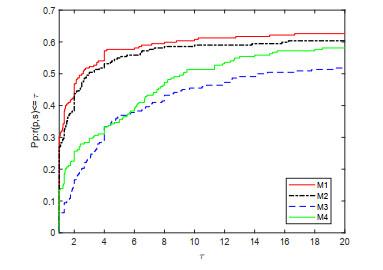
图 3
4.2 图像处理问题
在本节中, 我们将解决以下无约束优化问题, 以消除脉冲噪声
其中
我们的主要工作是从被脉冲噪声破坏的图像中恢复原始图像. 随着对图像处理需求的不断增加, 人们越来越关注如何利用优化方法来解决图像处理问题. 在这个实验中, 我们选择了三种不同的算法, 方法1、方法4和方法5来恢复相同的图像, 以对比三种算法的性能.
实验中使用的参数数据如下.
停止准则 如果条件
噪声信息
参数 本实验中使用的参数与上一个实验中使用的参数相同.
被测试问题 从被脉冲噪声破坏的图像中恢复原始图像. 本实验使用的图像分别是, Lena (
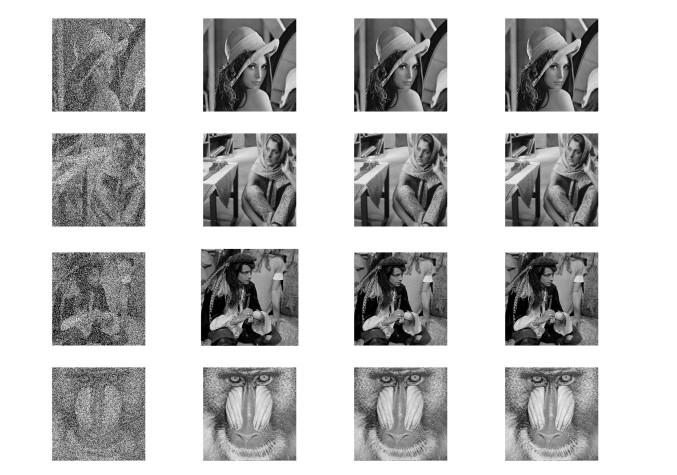
从图 4-6和表 1可以明显看出, 这三种算法都可以恢复被salt-and-pepper噪声损坏的图像, 无论是在噪音浓度25%、50%还是75%下都可以成果. 此外, 数据显示NHSDY算法(方法1)所使用的CPU时间要比方法4和方法5都短. 简言之, 不难得出以下结论: (ⅰ) 这三种算法在图像恢复应用中都是有效的; (ⅱ) 随着噪声浓度的增加, 所使用的CPU时间也随之增加, 即图像恢复的成本增加; (ⅲ) NHSDY算法(方法1)可以说是一种比较高效率的算法, 因为它相比其他两种算法可以在更短的CPU时间里完成任务, 表明新提出的这种算法具有很强的竞争力和良好的性能. 总之通过以上实验结果和分析可以得出结论, 新提出的算法有非常有前途和竞争力的.
图 4
图 5
图 6
表 1 三种方法的CPU时间
| 25%噪音浓度 | Lena | Barbara | Man | Baboom | 合计 |
| 方法1 | 6.016 | 31.188 | 7.781 | 7.281 | 52.266 |
| 方法4 | 6.563 | 33.094 | 8.641 | 7.75 | 56.048 |
| 方法5 | 6.359 | 33.578 | 8.859 | 7.515 | 56.311 |
| 50%噪音浓度 | Lena | Barbara | Man | Baboom | 合计 |
| 方法1 | 15.016 | 69.453 | 18.5 | 16.984 | 119.953 |
| 方法4 | 15.578 | 71.39 | 19.203 | 18.219 | 124.39 |
| 方法5 | 16.078 | 70.234 | 18.703 | 17.906 | 122.921 |
| 75% 噪音浓度 | Lena | Barbara | Man | Baboom | 合计 |
| 方法1 | 25.718 | 127.641 | 27.438 | 26.75 | 207.547 |
| 方法4 | 26.953 | 129.938 | 28.828 | 27.406 | 213.125 |
| 方法5 | 27.719 | 127.609 | 28.313 | 27.125 | 210.766 |
5 总结
本文提出了一种具有非单调线性搜索的三项共轭梯度算法, 其中搜索方向中的共轭参数是由两个著名共轭参数(HS和DY)组合成的凸组合形式. 给出的新方法具有以下优秀性质: (ⅰ) 在不需要假设和线性搜索的支持下, 满足了充分下降性质; (ⅱ) 在一定合理且常规的假设下, 建立了该方法在非凸函数的全局收敛性; (ⅲ) 函数的信息包含在搜索方向
今后, 有几个方面需要注意. 第一个问题是: 如果将凸组合的思想应用于拟牛顿法, 它是否也可以像本文提出的方法一样具有更好的性质?其次, 我们能否找到其他具有良好性质的共轭梯度公式吗?这可以说是今后的第二条工作. 众所周知, 共轭梯度算法在解决优化问题的有效方法中起着重要作用, 它应该被体现在近年来许多新的研究课题中, 这是我们今后工作的第三个方面.
数据的可用性 所有数据都包含在论文中, 可以使用.
利益问题 没有潜在的利益冲突.
参考文献
New properties of a nonlinear conjugate gradient method
DOI:10.1007/PL00005464 [本文引用: 1]
A globally convergent version of the Polak-Ribière conjugate gradient method
Restricted PR conjugate gradient method and its global convergence
Family weak conjugate gradient algorithms and their convergence analysis for nonconvex functions
The convergence properties of some new conjugate gradient methods
A short note on the global convergence of the unmodified PRP method
DOI:10.1007/s11590-012-0511-7 [本文引用: 1]
The PRP conjugate gradient algorithm with a modified WWP line search and its application in the image restoration problems
A PRP-based residual method for large-scale monotone nonlinear equations
The global convergence of the Polak-Ribière-Polyak conjugate gradient algorithm under inexact line search for nonconvex functions
Skewness of return distribution and coefficient of risk premium
DOI:10.1007/s11424-009-9170-x [本文引用: 1]
An unconstrained optimization test functions collection
Global convergence properties of conjugate gradient methods for optimization
DOI:10.1137/0802003
Global convergence of the Polak-Ribiere-Polyak conjugate gradient method with an Armijo-type inexact line search for nonconvex unconstrained optimization problems
DOI:10.1090/S0025-5718-08-02031-0
Globally convergent Polak-Ribière-Polyak conjugate gradient methods under a modified Wolfe line search
Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search
A modified PRP conjugate gradient algorithm with trust region for optimization problems
DOI:10.1080/01630563.2011.554948
On the Barzilai-Borwein gradient methods with structured secant equation for nonlinear least squares problems
DOI:10.1080/10556788.2020.1855170 [本文引用: 1]
A nonmonotone line search technique for Newton's method
A truncated Newton method with nonmonotone line search for unconstrained optimization
An assessment of nonmonotone linesearch techniques for unconstrained optimization
DOI:10.1137/S106482759427021X [本文引用: 1]
A structured quasi-Newton algorithm with nonmonotone search strategy for structured NLS problems and its application in robotic motion control
A nonmonotone line search technique and its application to unconstrained optimization
DOI:10.1137/S1052623403428208 [本文引用: 1]
Investigation on a class of nonmonotone cautious BFGS algorithms
On the nonmonotone line search
DOI:10.1023/A:1013653923062 [本文引用: 1]
An inexact line search approach using modified nonmonotone strategy for unconstrained optimization
Global convergence of the DY conjugate gradient method with Armijo line search for unconstrained optimization problems
DOI:10.1080/10556780600795748 [本文引用: 3]
A new nonmonotone line search technique for unconstrained optimization
DOI:10.1007/s11075-014-9866-4 [本文引用: 2]
Methods of conjugate gradients for solving linear systems
Function minimization by conjugate gradients
DOI:10.1093/comjnl/7.2.149 [本文引用: 2]
Note sur la convergence de méthodes de directions conjuguées
The conjugate gradient method in extremal problems
DOI:10.1016/0041-5553(69)90035-4 [本文引用: 1]
Efficient generalized conjugate gradient algorithms, part 1: theory
DOI:10.1007/BF00940464 [本文引用: 1]
A nonlinear conjugate gradient method with a strong global convergence property
DOI:10.1137/S1052623497318992 [本文引用: 2]
Convergence properties of algorithms for nonlinear optimization
A new conjugate gradient method with guaranteed descent and an efficient line search
DOI:10.1137/030601880 [本文引用: 1]
An efficient hybrid conjugate gradient method for unconstrained optimization
A derivative-free iterative method for nonlinear monotone equations with convex constraints
DOI:10.1007/s11075-018-0603-2 [本文引用: 2]
A descent modified Polak-Ribière-Polyak conjugate gradient method and its global convergence
DOI:10.1093/imanum/drl016 [本文引用: 1]
Derivative-free HS-DY-type method for solving nonlinear equations and image restoration
DOI:10.1016/j.heliyon.2020.e05400 [本文引用: 1]
Convergence analysis of a modified BFGS method on convex minimizations
DOI:10.1007/s10589-008-9219-0 [本文引用: 1]
Benchmarking optimization software with performance profiles
DOI:10.1007/s101070100263 [本文引用: 1]