1 引言
本文研究以下具有时滞和反馈控制的三种群非自治比率依赖型食物链模型的解的动力学行为
带有如下初始条件
其中
生物种群的持久性、全局吸引力和周期性是人口动力学的一个重要研究方向. 该模型(1.1)–(1.2)描述了三个物种之间的捕食性关系, 其中第二个种群捕食第一个种群, 第三个种群捕食第二个种群. 比率依赖的Lotka-Volterra捕食-食饵模型在参考文献[1, 11, 17, 19, 33, 37]中得到了广泛的研究, 并取得了许多优秀的结果. 2007年, Liang和Pan[17]通过构造李亚普诺夫函数, 研究了一类比率依赖的Holling-Tanner系统, 得到了该系统正平衡点的全局稳定性的充分条件. 在文献
此外, 我们都知道, 任何真实的生态和生物系统都总是受到环境噪声[9, 14, 24]的影响. 噪声不可避免地出现于远离平衡态的真实系统中, 特别是在Lotka-Volterra系统中, 因为生态系统和一般的生物和物理系统都是开放的系统, 它们不可避免地与环境相互作用. 系统与外部环境的相互作用导致了周期性的确定性外力, 在种群动力系统中, 这种随机噪声主要是乘法类型的随机扰动. 此外, 乘法噪声负责噪声诱导跃迁[15], 类似于相变现象, 发生在噪声强度较大的某些特定值, 使阶参量的概率密度函数在噪声强度的某些值下突然改变其形状. 因此, 对具有随机噪声扰动的Lotka-Volterra生态系统的研究无疑具有重要的物理数学意义, 它也使研究环境噪声对低压系统的积极影响成为可能[7, 27, 30]. 一些关于环境噪声对生态系统动力学性质的影响以及噪声在跨学科物理模型中的积极作用的结果, 可参见文献[5, 8, 12, 21, 28, 29].
然而, 据作者所知, 还没有人考虑同时具有时滞、比率依赖性和反馈控制的一般非自治的Lotka-Volterra系统. 在上述工作的激励下, 我们提出并研究上述三种群具有时滞和反馈控制的非自治比率依赖型Lotka-Volterra食物链模型. 本文的结构如下: 在第二节中, 给出了系统(1.1)–(1.2)的持久性条件. 第三节通过构造非负李亚普诺夫函数, 得到了保证系统正解全局吸引的充分条件. 第四节利用一些新的分析方法和Brouwer不动点理论, 得到了相应周期系统正周期解的存在性、唯一性和稳定性的一些充分条件. 最后, 在第五部分对上述系统进行了数值仿真, 验证了所得的理论结果. 另外, 对具有乘法噪声的上述系统进行了数值仿真, 发现该模型一些新的有趣的动力学行为.
2 持久性
我们首先介绍以下定义和符号, 以获得系统
定义2.1 如果存在正常数
作为文献[4]中引理2.1的直接推论, 我们有下述引理.
引理2.1 如果
以下两个引理来自文献[23], 它们将被用于证明系统
引理2.2 对初值
其中
其中
引理2.3 假设
如果
对于系统
定理2.1 若系统
那么系统
证 由系统
根据引理2.2, 我们得到
根据系统
根据引理
根据系统
根据引理2.1, 我们可以得到
根据系统
根据引理
另一方面, 根据系统
根据假设
根据系统
根据引理
由系统
如果
根据系统
根据引理
根据(2.2)–(2.13)式, 可知系统
3 全局吸引性
在本节中, 我们取得了一些保证捕食-食饵系统
定义3.1 假设
那么系统
引理3.1[16, 引理8.2] 如果函数
定理3.1 假设系统
其中
那么系统
证 假设
我们定义
计算
接下来, 我们定义
于是, 根据
定义
设
根据(3.3)–(3.4)式, 计算
类似地, 我们定义
定义
然后, 根据
定义
令
由
类似地, 我们定义
于是, 我们可得
接下来, 定义
于是, 我们有
定义
设
于是, 我们有
定义
计算
及
进一步, 考虑李雅普诺夫泛函
于是, 根据
根据定理
对
所以
根据
利用定理
因此, 系统
4 周期解
在本节中, 我们将利用上述结果和不动点理论, 探讨参数为连续正
引理4.1[2] 设
定理4.1 设条件
证 根据泛函微分方程解的存在唯一性定理, 我们可以定义一个Poincaré映射
那么
5 数值模拟
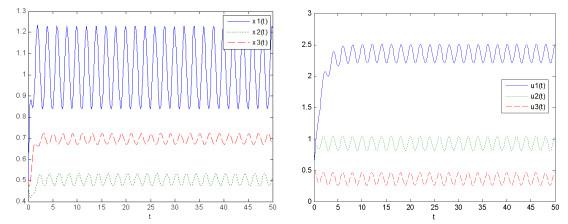
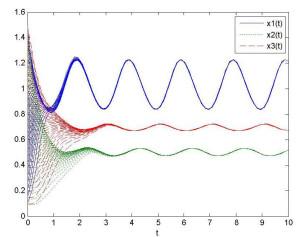
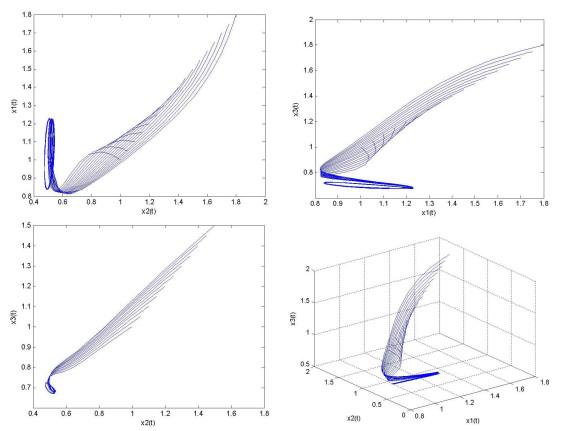
基于种群的周期性增长和生长环境的周期性, 我们选择了合适的周期系数来验证上述理论结果. 为此, 我们考虑如下带有多时滞和反馈控制的三种群Lotka-Volterra比率依赖食物链模型:
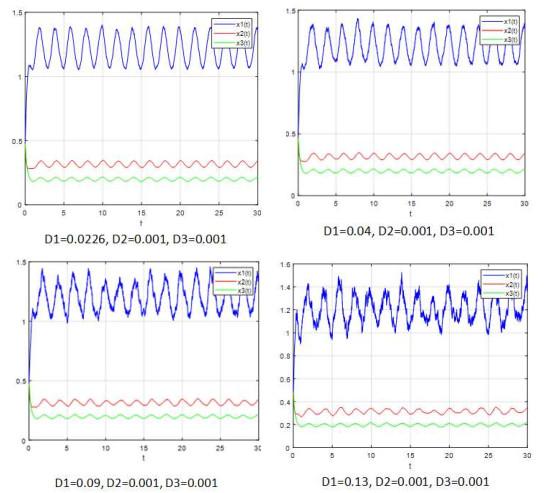
图 1
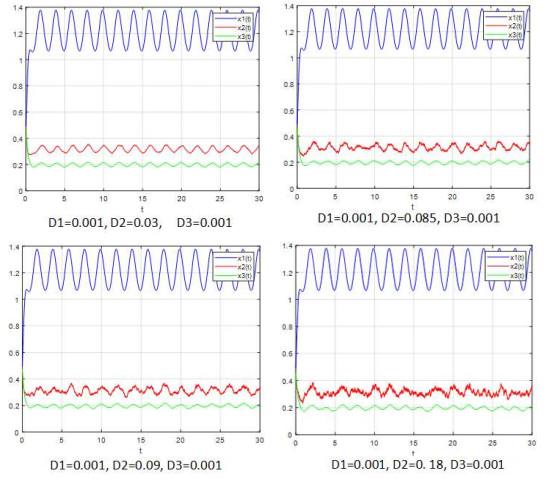
图 2
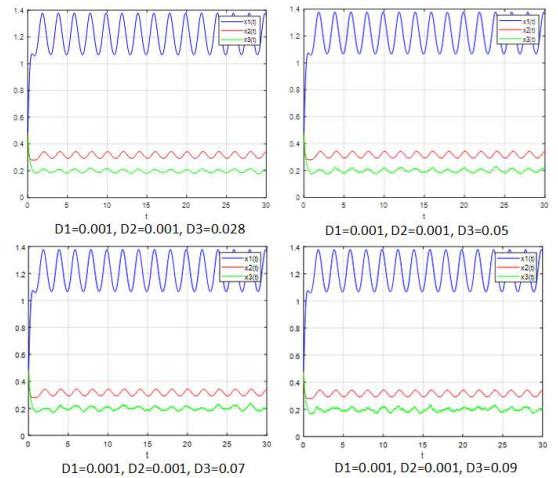
图 3
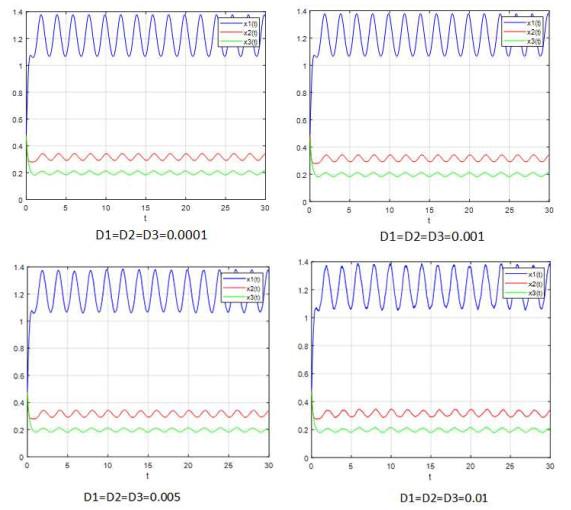
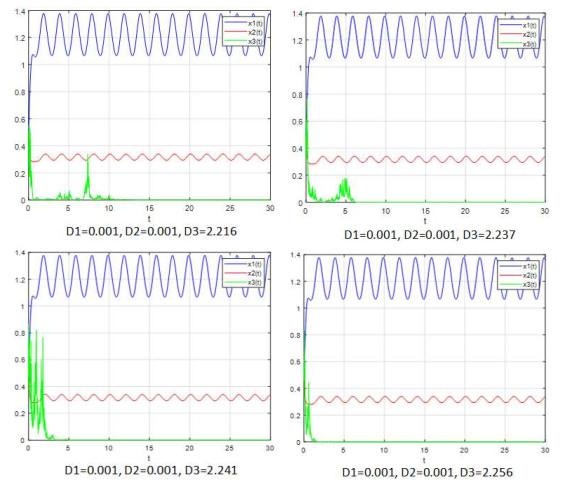
为了观察噪声对三种群食物链Lotka-Volterra系统
其中
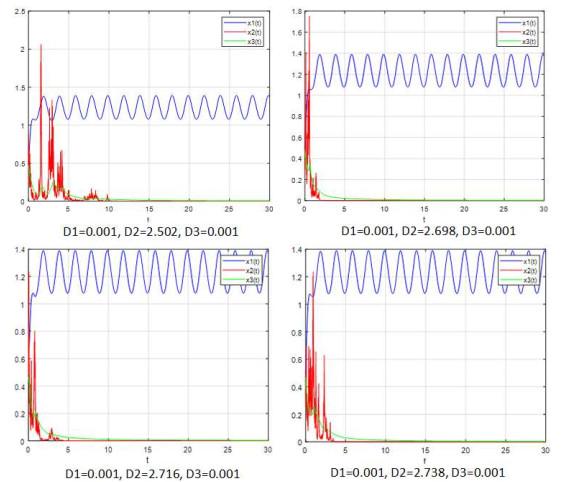
图 4
图 5
图 6
图 7
图 8
图 9
图 10
从图 4中, 我们可以发现, 当噪声强度非常低时, 新的随机模型(5.3)–(5.4)具有几乎确定的周期解. 此外, 图 5显示, 当噪声强度
6 结论
在本文中, 我们提出并研究了一类具有时滞和反馈控制的非线性非自治三种群比率依赖型食物链模型. 通过改进一些现有的方法, 尤其是针对具有反馈控制项的时滞微分方程构造Lyapunov函数的技巧, 研究了系统
参考文献
Coupling in predator-prey dynamics: Ratio-dependence
DOI:10.1016/S0022-5193(89)80211-5 [本文引用: 1]
Stability and Hopf Bifurcation in a delayed ratio dependent Holling-Tanner type model
DOI:10.1016/j.amc.2014.11.086 [本文引用: 1]
On a nonlinear nonautonomous predator-prey model with diffusion and distributed delay
DOI:10.1016/j.cam.2004.10.001 [本文引用: 1]
Spatio-temporal behaviour of the deep chlorophyll maximum in Mediterranean Sea: Development of a stochastic model for picophytoplankton dynamics
DOI:10.1016/j.ecocom.2012.10.002 [本文引用: 1]
Global dynamics of a ratio-dependent holling-tanner predator-prey system
DOI:10.1016/j.jmaa.2017.11.057 [本文引用: 1]
Verhulst model with lévy white noise excitation
DOI:10.1140/epjb/e2008-00337-0 [本文引用: 1]
Analysis of dynamics in a complex food chain with ratio-dependent functional response
Optimal forager against ideal free distributed prey
A stochastic interspecific competition model to predict the behaviour of Listeria monocytogenes in the fermentation process of a traditional Sicilian salami
DOI:10.1007/s00217-008-0988-6 [本文引用: 1]
Global attractivity in a competition system with feedback controls
Qualitative analysis of a ratio-dependent holling-tanner model
Periodic solution of a leslie predator-prey system with ratio-dependent and state impulsive feedback control
DOI:10.1007/s11071-017-3637-4 [本文引用: 1]
Dynamics of a predator-prey model with harvesting and reserve area for prey in the presence of competition and toxicity
Delay effect on the permanence for lotka-volterra cooperative systems
DOI:10.1016/j.nonrwa.2009.10.005 [本文引用: 1]
Field- and irradiation-induced phenomena in memristive nanomaterials
DOI:10.1002/pssc.201600083 [本文引用: 1]
Dynamical behavior for a class of delayed competitive-mutualism systems
DOI:10.1007/s12591-014-0226-6 [本文引用: 1]
Permanence for nonautonomous Lotka-Volterra cooperative systems with delays
DOI:10.1016/j.nonrwa.2009.01.002 [本文引用: 3]
Permanence and stability in non-autonomous predator-prey Lotka-Volterra systems with feedback controls
Permanence and extinction of a three-species ratio-dependent food chain model with delay and prey diffusion
DOI:10.1016/j.amc.2010.02.037 [本文引用: 2]
Role of the noise on the transient dynamics of an ecosystem of interacting species
Lifetime of metastable states and suppression of noise in interdisciplinary physical models
Volatility effects on the escape time in financial market models
DOI:10.1142/S0218127408022007 [本文引用: 1]
Moment equations for a spatially extended system of two competing species
On a multi-delay lotka-volterra predator-prey model with feedback controls and prey diffusion
Evolution of mobility in predator-prey systems
DOI:10.3934/dcdsb.2014.19.3397 [本文引用: 2]
Persistence and global stability in a delayed predator-prey system with michaelis-menten type functional response
Ersistence and global stability for a delayed nonautonomous predator-prey system without dominating instantaneous negative feedback
DOI:10.1006/jmaa.2001.7524 [本文引用: 2]
Coexistence of a diffusive predator-prey model with holling type-Ⅱ functional response and density dependent mortality
DOI:10.1016/j.jmaa.2011.07.027 [本文引用: 1]