研究结构化的种群动力系统控制问题的动机有三: 维护生态平衡和生物多样性; 利用种群资源获取最大经济利益; 探索一些有趣也有挑战性的无穷维系统问题. 学者们对此做了巨大的努力, 也获得了丰富成果. 对于年龄结构系统可参见文献[1-20]; 离散阶段结构模型参见文献[1]; 涉及空间分布的模型可参见文献[4] 和 [21]; 尺度结构系统可参见文献[5]. 这些工作关注的问题包括最优解的存在性, 最优性条件, 最优解的逼近和具体应用等, 大大增进了对于结构化种群系统调控的理解, 也是进一步发展的出发点.

大量生态学研究成果表明：许多种群内部的个体之间确实存在等级(或称社会地位)差异(参见综述文献[22]), 也有一些工作是借助数学模型法完成的(参见文献[23-30]). 概要而言, 在现有的等级结构种群系统的模型化工作中, 关注的主要问题包括适定性、平衡态及其稳定性、种内竞争与振动、模型的数值解法等, 属于演化动力学范畴, 相关的控制问题研究成果很少见. 虽然系统的行为分析很重要, 但那些与环境保护和人类利益密切相关的控制问题（如能控性和最优控制）也不应当被忽略.

本文考察一类非线性等级结构种群模型的最优收获问题, 系统由两个相互竞争的种群构成. 模型的主要特点是含有所谓“内部环境”, 它依赖于个体年龄并对繁殖率和死亡率产生影响. 粗略而言, 内部环境就是年长者与加权后的年轻者之和, 它依赖于瞬时年龄, 不同年龄的个体所面临的内部环境也不同. 本文力图在具有相互作用的等级结构种群系统控制问题方面取得进展. 下一节描述群落模型与最优控制问题, 第3节证明最优策略的存在性；第4节提出并确立最大值原理, 利用共轭系统和反馈形式刻画最优收获强度. 完成这一任务需要建立一个新的连续性结果. 第5节利用数值方法考察价格变化对最优策略及最优效益的影响, 最后一节总结全文.

本文考察下列最优控制问题

(2.1) $ \begin{equation} \max\limits_{u\in{\cal U}}J(u): = \sum\limits_{i = 1}^2 {\int_0^A {\int_0^T {{g_i}(a){u_i}(a, t){p_i}(a, t){\rm{d}}t{\rm{d}}a} } }, \end{equation} $

其中$ u_i $表示人对种群$ i $中个体的收获强度, 它满足

$ {u_i} \in {{\cal U}}_i: = \left\{ {{v} \in {L^\infty }({Q_T}):0 \le {v}(a, t) \le U_i, \forall (a, t)\in Q_T} \right\}, $

$ U_i $为给定常数, $ u=(u_1, u_2)\in {\cal U}:={{\cal U}}_1\times{{\cal U}}_2 $, $ g_i\in {L^\infty}([0, A]) $代表种群$ i $中年龄为$ a $的个体的经济价值, $ (u_i, p_i) $满足下列状态系统方程

(2.2) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial p_i}{\partial t} + \frac{\partial p_i}{\partial a} = -\mu _{i}\left( a, E(p_1)(a, t), E(p_2)(a, t)\right)p_i(a, t)-u_i(a, t)p_i(a, t), \quad({a, t}) \in Q_{T}, \\ { } p_i(0, t) = \int_0^{A} \beta_i(a, E(p_i)(a, t))p_i(a, t){\rm d}a, \quad t \in(0, T), \\ p_i(a, 0) = p_i^0(a), \quad a \in [0, A], \\ { } E(p_i)({a, t}) = \alpha_i \int_0^a {p_i}( r, t) {\rm d}r + \int_a^{A} p_i(r, t){\rm d}r, \;\quad (a, t)\in Q_{T}, 0\leq\alpha_i <1; i=1, 2. \end{array} \right. \end{equation} $

在以上模型(2.2) 中, $ Q_{T}=[0, A]\times[0, T) $, 正常数$ A $和$ T $分别表示两种群个体最大年龄和控制周期. $ p_1(a, t), p_2(a, t) $分别代表$ t $时刻两竞争种群的年龄密度函数, 而$ p_i^0(a) $表示初始年龄分布. 常数$ \alpha_i $表征对种群$ i $中年龄小于$ a $的个体的折扣系数, 体现了比年长个体较弱的竞争力. 函数$ \mu_i, \beta_i $分别表示种群$ i $中个体的死亡率和繁殖率. $ E(p_i) $称为种群$ i $中的内部环境.

本文假定下述条件成立($ i=1, 2 $).

(An1) 对任意$ (a, x)\in[0, A]\times[0, +\infty), $有$ 0\le\beta_i(a, x)\le\beta_i^* $且$ \beta_i^* $为常数; 对给定的$ M>0 $, 存在$ L_1(M)>0 $, 使得: 当$ x_1, x_2\in [0, M] $时有$ \vert \beta_i(a, x_1)-\beta_i(a, x_2) \vert \le L_1(M) \vert x_1 - x_2 \vert $;

(An2) 对任意$ (a, x, y)\in[0, A]\times[0, +\infty)\times[0, +\infty), $有$ \mu_i(a, x, y)>0, $$ \mu_i(a, x, y)\in L_{loc}^1[0, A] $且$ \int_0^A\mu_i(a, x, y){\rm d}a=+\infty $; 对给定的$ M>0, $存在$ L_2(M)>0 $使得: 当$ x_i, y_i\in[0, M] $时有

$ \vert\mu_i(a, x_1, y_1)-\mu_i(a, x_2, y_2) \vert \le L_2(M) \left(\vert x_1 - x_2 \vert+\vert y_1 - y_2 \vert\right); $

$ \mu_{ix}(a, x, y)>0, \mu_{iy}(a, x, y)>0 $, 其中$ \mu_{ix}, \mu_{iy} $分别表示函数$ \mu_i $对变量$ x, y $的偏导数.

(An3) 对任意$ a\in [0, A] $, 有$ 0 \le p_i^0(a) \le P_i $且$ P_i $为常数.

文献[31] 已经证明了如下结论.

引理2.1  对任意给定的$ u\in{\cal U} $, 模型系统$ (2.2) $存在唯一的解$ p^{u}=(p_1^u, p_2^u) $, 满足$ 0\le p_i^u (a, t)\le \overline{M}_i, i=1, 2 $, $ \overline{M}_i $为常数.

刻画最优策略需要应用下列结果.

引理2.2  系统$ (2.2) $的解$ p^{u}\in[L^{\infty}(Q_T)]^2 $关于控制变量$ u\in{\cal U} $连续.

证  令$ u^i=\left(u_1^i, u_2^i\right), p^i=\left(p_1^i, p_2^i\right), i=1, 2 $; $ (u^i, p^i) $满足$ (2.2) $式. 由特征线法可知

(2.3) $ \begin{equation} p_i(a, t)= \left\{\begin{array}{ll} p_i^0(a-t)\Pi_i(a, t, t), \quad &a\geq t; \\ b_i(t-a)\Pi_i(a, t, a), \quad &a< t, \end{array}\right. \end{equation} $

其中

(2.4) $ \begin{eqnarray} \Pi_i(a, t, s) &=&\exp\bigg\{-\int_0^s\big[\mu_i\left(a-\tau, E(p_1)(a-\tau, t-\tau), E(p_2)(a-\tau, t-\tau)\right) {}\\ &&+u_i(a-\tau, t-\tau)\big]{\rm d}\tau\bigg\}, \end{eqnarray} $

(2.5) $ \begin{equation} b_i(t)=F_i(t)+\int_0^tK_i(t, s)b_i(t-s){\rm d}s, \quad t\in(0, T), \end{equation} $

(2.6) $ \begin{equation} K_i(t, a)= \left\{\begin{array}{ll} \beta_i(a, E(p_i)(a, t))\Pi_i(a, t, a), \quad & a.e.\;(a, t)\in Q_T; \\ 0, \quad &\mbox{其它}, \end{array}\right. \end{equation} $

(2.7) $ \begin{equation} F_i(t)= \left\{\begin{array}{ll} { } \int_0^A \beta_i(a+t, E(p_i)(a+t, t))p_i^0(a)\Pi_i(a+t, t, t){\rm d}a, &a.e.\;t\in(0, \min (A, T)); \\ 0, \quad &\mbox{其它}. \end{array}\right. \end{equation} $

以下假设$ T>A $; 相反情形可以类似处理.

根据Bellmann不等式和方程$ (2.5) $可知: $ 0\le b_i(t)\le B_i, i=1, 2 $, $ B_i $为常数. 若$ a\ge t $, 则等式(2.3)–(2.4) 意味着

(2.8) $ \begin{eqnarray} \left|p_1^1(a, t)-p_1^2(a, t)\right| &=&\left|p_1^{0}(a-t)\Pi_1^1(a, t, t)-p_1^0(a-t)\Pi_1^2(a, t, t)\right|{}\\ &\le &p_1^{0}(a-t)\bigg| \int_{0}^{t}{ \Big[ \mu _{1}\left( a, E(p_{1}^{1})(a-\tau , t-\tau ), E(p_{2}^{1})(a-\tau , t-\tau ) \right) } {}\\ && -\mu _{1}\left( a, E(p_{1}^{2})(a-\tau , t-\tau ), E(p_{2}^{2})(a-\tau , t-\tau ) \right){}\\ && +u_{1}^{1}(a-\tau , t-\tau )-u_{1}^{2}(a-\tau , t-\tau ) \Big]{\rm d}\tau \bigg|{}\\ &\le& P_1 L_2(M)\int_{0}^{t}{\Big[ \left| E(p_{1}^{1})(a-\tau , t-\tau )-E(p_{1}^{2})(a-\tau , t-\tau ) \right| }{}\\ && +\left| E(p_{2}^{1})(a-\tau , t-\tau )-E(p_{2}^{2})(a-\tau , t-\tau ) \right| \Big] {\rm d}\tau+ P_1 T\parallel u^1_1 -u^2_1\parallel{}\\ &\le &P_1 T\parallel u^1_1 -u^2_1\parallel +P_1 L_2(M)\int_{0}^{t} {\bigg[\int_{0}^{A }{\left| p_{1}^{1}(r, y )-p_{1}^{2}(r, y ) \right|{\rm d}r} }{}\\ && +\int_{0}^{A}{\left| p_{2}^{1}(r, y)-p_{2}^{2}(r, y) \right|{\rm d}r} \bigg]{\rm d}y{}\\ &\le& P_1 T\parallel u^1_1 -u^2_1\parallel +P_1 L_2(M)A\int_0^t{\left\| p^{1}(\cdot, s)-p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s. \end{eqnarray} $

类似地, 若$ a<t $, 则有

(2.9) $ \begin{eqnarray} &&\left|p_1^1(a, t)-p_1^2(a, t)\right|{}\\ &=&\left|b_1(t-a;u^1)\Pi_1^1(a, t, a)-b_1(t-a;u^2)\Pi_1^2(a, t, a)\right|{}\\ &\le& \left|b_1(t-a;u^1)-b_1(t-a;u^2)\right|\Pi_1^1(a, t, a){}\\ && +\left|\Pi_1^1(a, t, a)-\Pi_1^2(a, t, a)\right|b_1(t-a;u^2){}\\ &\le &\left|b_1(t-a;u^1)-b_1(t-a;u^2)\right|+B_1 A{\left\|u_1^1-u_1^2\right\|}_{L^\infty(Q_T)}{}\\ && +B_1 L_2(M)\int_{0}^{a}{\bigg[\int_{0}^{A }{\left| p_{1}^{1}(r, s )-p_{1}^{2}(r, s) \right|{\rm d}r} +\int_{0}^{A}{\left| p_{2}^{1}(r, s )-p_{2}^{2}(r, s ) \right|{\rm d}r} \bigg]}{\rm d}s{} \\ &\le& \left|b_1(t-a;u^1)-b_1(t-a;u^2)\right|+B_1 A{\left\|u_1^1-u_1^2\right\|}_{L^\infty(Q_T)}{}\\ && +B_1L_2(M)A\int_{0}^{a}{\left\| p_{1}^{1}(\cdot, s)-p_{1}^{2}(\cdot, s ) \right\|_{L^\infty(0, A)}{\rm d}s}{}\\ &&+B_1L_2(M)A\int_{0}^{a}{\left\| p_{2}^{1}(\cdot, s )-p_{2}^{2}(\cdot, s ) \right\|_{L^\infty(0, A)}{\rm d}s}{}\\ &\le &\left|b_1(t-a;u^1)-b_1(t-a;u^2)\right|+B_1 A{\left\|u_1^1-u_1^2\right\|}_{L^\infty(Q_T)}{}\\ && +B_1L_2(M)A\int_{0}^{t}{\left\| p^{1}(\cdot, s)-p^{2} (\cdot, s)\right\|_{[L^\infty(0, A)]^2}{\rm d}s}. \end{eqnarray} $

由$ (2.5) $式可导出

(2.10) $ \begin{eqnarray} &&\left|b_1(t-a;u^1)-b_1(t-a;u^2)\right|{}\\ &\le & \left|F_1(t-a;u^1)-F_1(t-a;u^2)\right| +\int_0^t K_1(t-s, s;u^2)\left|b_1(s;u^1)-b_1(s;u^2)\right|{\rm d}s{}\\ & &+\int_0^t\left|K_1(t-s, s;u^1)-K_1(t-s, s;u^2)\right|b_1(s;u^1){\rm d}s. \end{eqnarray} $

利用表达式$ (2.7) $可得

$ \begin{eqnarray} && \left|F_1(t-a;u^1)-F_1(t-a;u^2)\right|\\ &\le& \int_0^A {\left| {\beta _1 (t, E(p_1^1 )(t, t-a)) - \beta _1 (t, E(p_1^2)(t, t-a))} \right|}{p_1^0} (a)\Pi _1^1 (t, t-a, t-a){\rm d}a\\ && + \int_0^A {\beta _1 (t, E(p_1^2)(t, t-a))p_1^0 (a)}\left| {\Pi _1^1 (t, t-a, t-a) - \Pi _1^2 (t, t-a, t-a)} \right|{\rm d}a\\ &&\times \left|F_1(t-a;u^1)-F_1(t-a;u^2)\right|\\ &\le &P_1 L_1(M)\int_0^A {\left|E(p_1^1 )(t, t-a)-E(p_1^2)(t, t-a)\right|}{\rm d}a\\ && + P_1\beta_1^*\int_0^A \left| {\Pi _1^1 (t, t-a, t-a) - \Pi _1^2 (t, t-a, t-a)} \right|{\rm d}a\\ & \le& C_0 \Big( \parallel u^1 -u^2\parallel +\int_0^t \parallel p_1 (\cdot, s)-p_2 (\cdot, s)\parallel_{(L^{\infty}(Q_T))^2}{\rm d}s\Big), \end{eqnarray} $

其中$ C_0 $为常数. 据$ (2.6) $式推出

(2.11) $ \begin{eqnarray} &&\int_0^t\left|K_1(t-s, s;u^1)-K_1(t-s, s;u^2)\right|b_1(s;u^1){\rm d}s{}\\ &\le& B_1\int_0^t\left|\beta_1(s, E(p_1^1)(s, t-s))-\beta_1(s, E(p_1^2)(s, t-s))\right|{\rm d}s{}\\ && + B_1\beta_1^*\int_0^t{\left| {\Pi _1^1 (s, t-s, s) - \Pi _1^2 (s, t-s, s)} \right|{\rm d}s}{}\\ &\le& C\left( \parallel u_1^1 -u_1^2\parallel_{L^{\infty}(Q_T)}+\int_0^t{\left\| p^{1}(\cdot, s) -p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s\right). \end{eqnarray} $

此外

(2.12) $ \begin{equation} \int_{0}^{t}{{{K}_{1}}}(t-s, s;{{u}^{2}})\left| {{b}_{1}}(s;{{u}^{1}})-{{b}_{1}}(s;{{u}^{2}}) \right|{\rm d}s\le \beta _{1}^{*}\int_{0}^{t}{\left| {{b}_{1}}(s;{{u}^{1}})-{{b}_{1}}(s;{{u}^{2}}) \right|}{\rm d}s. \end{equation} $

结合关系式$ (2.10) $与(2.11)–(2.12) 并运用Gronwall不等式可知: 存在常数$ C_1, C_2>0 $, 使得

(2.13) $ \begin{equation} \left\|b_1(\cdot;u^1)-b_1(\cdot;u^2)\right\|_{L^\infty(0, T)} \le C_1{\left\|u_1^1-u_1^2\right\|}_{L^\infty(Q_T)}+C_2\int_0^t{\left\| p^{1}( \cdot, s)-p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s. \end{equation} $

将$ (2.13) $式代入$ (2.9) $式, 可得

$ \begin{eqnarray} \left\|p_1^1(\cdot, t)-p_1^2(\cdot, t)\right\|_{L^\infty(0, A)} \le C_3{\left\|u_1^1-u_1^2\right\|}_{L^\infty(Q_T)}+C_4\int_0^t{\left\| p^{1}(\cdot, s)-p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s, \end{eqnarray} $

其中$ C_3 $和$ C_4 $均为常数. 类似可得下列不等式

$ \begin{eqnarray} \left\|p_2^1(\cdot, t)-p_2^2(\cdot, t)\right\|_{L^\infty(0, A)} \le \overline{C}_3{\left\|u_2^1-u_2^2\right\|}_{L^\infty(Q_T)}+\overline{C}_4\int_0^t{\left\| p^{1}(\cdot, s)-p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s. \end{eqnarray} $

因此

$ \begin{eqnarray} \left\|p^1(\cdot, t)-p^2(\cdot, t)\right\|_{[L^\infty(0, A)]^2}&\le &\left(C_3+\overline{C}_3\right){\left\|u^1-u^2\right\|}_{[L^\infty(Q_T)]^2}\\ &&+(C_4+\overline{C}_4)\int_0^t{\left\| p^{1}(\cdot, s)-p^{2}(\cdot, s)\right\|}_{[L^\infty(0, A)]^2}{\rm d}s. \end{eqnarray} $

再次应用Gronwall不等式, 即可推出

$ \left\|p^1(\cdot, t)-p^2(\cdot, t)\right\|_{[L^\infty(0, A)]^2}\le C{\left\|u^1-u^2\right\|}_{[L^\infty(Q_T)]^2}, $

这意味着

$ {{\left\| {{p}^{1}}-{{p}^{2}}\right\|}_{{{[{{L}^{\infty }}({{Q}_{T}})]}^{2}}}}\le C{\left\|u^1-u^2\right\|}_{[L^\infty(0, T)]^2}, $

其中常数$ C $不依赖于$ u^i, i=1, 2 $.

引理3.1  令$ \varepsilon>0 $充分小. 若存在常数$ M_i>A\overline{M}, i=1, 2, \overline{M}=\max\{\overline{M}_1, \overline{M}_2\} $, 使得

$ \alpha_i \int_0^a \mu_i(r, M_1, M_2) {\rm d}r + \int_a^{A-\varepsilon} \mu_i(r, M_1, M_2){\rm d}r $

在$ [0, A-\varepsilon] $上有界, 则集合$ \{E(p_i^{u}):u\in {\cal U}\} $在空间$ L^2(Q_T) $中预紧.

证  对于给定的$ \varepsilon>0 $, 定义如下截断环境

$ E^{\varepsilon}(p_i^u)(a, t)=\alpha_i \int_0^a p_i^{u}( r, t) {\rm d}r + \int_a^{A-\varepsilon} p_i^{u}(r, t){\rm d}r, (a, t)\in Q_T. $

在系统$ (2.2) $中的第一式对变量$ a $在区间$ [0, A-\varepsilon] $上积分, 可得

$ \begin{eqnarray} && \alpha_i\int_0^a\bigg[ \frac{\partial p^{u}_i(r, t)}{\partial t} + \frac{\partial p^{u}_i(r, t)}{\partial r}\bigg]{\rm d}r+ \int_a^{A-\varepsilon}\bigg[ \frac{\partial p^{u}_i(r, t)}{\partial t} + \frac{\partial p^{u}_i(r, t)}{\partial r}\bigg]{\rm d}r\\ &=&-\left\{\alpha_i\int_0^a\big[\mu_i(r, E(p_1^{u})(r, t), E(p_2^{u})(r, t))+u_i(r, t)\big]p^{u}_i(r, t){\rm d}r\right.\\ && \left.+\int_a^{A-\varepsilon}\big[\mu_i(r, E(p_1^{u})(r, t), E(p_2^{u})(r, t))+u_i(r, t)\big]p^{u}_i(r, t){\rm d}r\right\}. \end{eqnarray} $

由上式和$ (2.2) $式中的第三式可推出

$ \begin{eqnarray} \frac{\partial E^{\varepsilon}(p_i^{u})(a, t)}{\partial t}&=&-\left\{\alpha_i\int_0^a \big[\mu_i(r, E(p_1^{u})(r, t), E(p_2^{u})(r, t))+u_i(r, t)\big]p^{u}_i(r, t){\rm d}r\right.\\ &&\left.+\int_a^{A-\varepsilon}\big[\mu_i(r, E(p_1^{u})(r, t), E(p_2^{u})(r, t))+u_i(r, t)\big]p^{u}_i(r, t){\rm d}r\right\}\\ && -\bigg[(\alpha_i-1){p^{u}_i(a, t)}+p^{u}_i(A-\varepsilon, t)-\alpha_i\int_0^{A} \beta_i(r, E(p_i^{u})(r, t))p^{u}_i(r, t){\rm d}r\bigg]. \end{eqnarray} $

引理条件保证了$ \frac{\partial E^{\varepsilon}(p_i^{u})(a, t)}{\partial t} $关于$ u $一致有界. 此外, 由$ \frac{\partial E^{\varepsilon}(p_i^{u})(a, t)}{\partial a}=(\alpha_i-1)p^{u}_i(a, t) $知: $ \frac{\partial E^{\varepsilon}(p_i^{u})(a, t)}{\partial a} $也关于$ u $一致有界.

以下运用Fréchet-Kolmogorov定理^{[32, p275]}证明集合$ \{E^{\varepsilon}(p_i^{u}):u\in {\cal U}\} $在$ L^2(Q_T) $中预紧.

拓展函数$ E^{\varepsilon}(p_i^{u}) $的定义域: 当$ (a, t)\in R^2-Q_T $时, 令$ E^{\varepsilon}(p_i^{u})(a, t)=0 $. 易知

(3.1) $ \begin{equation} \sup\limits_{u\in {\cal U}} \int_{{{R}^{2}}}{{{[{{E}^{\varepsilon }} ({{p}_{i}^{u}})(a, t)]}^{2}}{\rm d}a{\rm d}t<\infty }, \end{equation} $

(3.2) $ \lim \limits_{r \rightarrow \infty \atop l \rightarrow \infty} \int_{|a|>r \atop|t|>l}\left[E^{\varepsilon}\left(p_{i}^{u}\right)(a, t)\right]^{2} \mathrm{d} a \mathrm{d} t=0$

记$ \sup \limits_{u \in {\cal U}}\left|\frac{\partial E^{\varepsilon} (p_i^{u})(a, t)}{\partial a}\right|=N_1, \mathop {\sup }\limits_{u \in {\cal U}}\left| \frac{\partial E^{\varepsilon}(p_i^{u})(a, t)}{\partial t}\right|=N_2 $. 注意下列关系

$ \begin{eqnarray} && \int_0^T {\int_0^A {{{\left[ {{E^{\varepsilon }}({p_i^{u}})(a + \Delta a, t + \Delta t) - {E^{\varepsilon }}({p_i^{u}})(a, t)} \right]}^2}{\rm{d}}a{\rm{d}}t} }\\ &=& \int_0^T {\int_0^A {\left[ {{E^{\varepsilon }}({p_i^{u}})(a + \Delta a, t + \Delta t) - {E^{\varepsilon }}({p_i^{u}})(a, t + \Delta t)} \right.} }\\ &&\left. { + {E^{\varepsilon }}({p_i^{u}})(a, t + \Delta t) - {E^{\varepsilon }} ({p_i^{u}})(a, t)} \right]^2{\rm{d}}a{\rm{d}}t\\ &=&\int_0^T {\int_0^A {{{\left[ {\frac{{\partial {E^{\varepsilon }}({p_i^{u}})(a + {\theta _1}\Delta a, t + \Delta t)}}{{\partial a}}\Delta a + \frac{{\partial {E^{\varepsilon }}({p_i^{u}})(a, t + {\theta _2}\Delta t)}}{{\partial t}}\Delta t} \right]}^2}{\rm{d}}a{\rm{d}}t} }\\ &\le& \int_0^T {\int_0^A {{{( {{N_1}\Delta a + {N_2}\Delta t} )}^2}{\rm{d}}a{\rm{d}}t} }\\ &\le& AT{( {{N_1}\Delta a + {N_2}\Delta t} )}^2, \end{eqnarray} $

其中$ \theta_1, \theta_2\in [0, 1] $, 由此即知

(3.3) $ \lim \limits_{\Delta a \rightarrow 0 \atop \Delta t \rightarrow 0} \int_{0}^{T} \int_{0}^{A}\left[E^{\varepsilon}\left(p_{i}^{u}\right)(a+\Delta a, t+\Delta t)-E^{\varepsilon}\left(p_{i}^{u}\right)(a, t)\right]^{2} \mathrm{~d} a \mathrm{d} t=0 $

关于$ u $一致成立. 因此, Fréchet-Kolmogorov定理断言集合$ \{E^{\varepsilon}(p_i^{u}):u\in {\cal U}\} $的预紧性.

另一方面, 解$ p^{u} $关于$ u $的一致有界性意味着

$ \left|E(p_i^{u})(a, t)-E^{\varepsilon}(p_i^{u})(a, t)\right|=\int_{A-\varepsilon}^A{p_i^{u}(a, t){\rm d}a}\le \varepsilon\overline{M}, \quad \forall (a, t)\in Q_T, \quad\forall u\in {\cal U}. $

所以, 环境集$ \{E(p_i^{u}):u\in {\cal U}\} $在$ L^2(Q_T) $中预紧.

定理3.1  若引理3.1的条件成立, 则控制问题$ (2.1) $–$ (2.2) $至少存在一个最优解.

证  记$ d=\mathop {\sup }\limits_{u \in {\cal U}} J(u) $. 由引理2.1知$ 0\le d<+\infty $.

考虑任一最大化序列$ \left\{u^n=(u_{1}^n, u_{2}^n):{u^n}\in{\cal U}\right\}, n\in N^* $ (自然数集), 使得

(3.4) $ \begin{eqnarray} d-\frac{1}{n}<J({u^n})\le d. \end{eqnarray} $

因$ \{p^{u^n}\}\subset L^2 (Q_T) $有界, 故存在子序列(仍记为$ \{p^{u^n}\} $) 使得

(3.5) $ \begin{eqnarray} p^{u^n}=(p_1^{u^n}, p_2^{u^n}) \mathop{\rightarrow }\limits^{\mbox弱} p^*=(p_1^*, p_2^*), \quad n\rightarrow \infty. \end{eqnarray} $

此外, 引理3.1意味着: 存在子序列(仍记为$ \{u^n\} $) 满足

(3.6) $ \begin{equation} E(p_i^{u^n}) \rightarrow E(p_i^{u^*})\in L^2(Q_T), n\rightarrow \infty, \end{equation} $

(3.7) $ \begin{equation} E(p_i^{u^n})(a, t) \rightarrow E(p_i^{u^*})(a, t), \quad a.e. (a, t)\in Q_T, n\rightarrow \infty. \end{equation} $

应用Mazur定理^{[2, p69]}可知: 存在数$ \lambda_k^n $及如下函数

(3.8) $ \begin{eqnarray} \widetilde{p}_i^n(a, t)=\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}p_{i}^{u^{k}}(a, t), \quad \lambda _{k}^{n}\ge 0, \quad \sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}}}=1, \end{eqnarray} $

使得

(3.9) $ \begin{eqnarray} \widetilde{p}^n \rightarrow p^*, n\rightarrow \infty. \end{eqnarray} $

定义新的控制序列$ \left\{\widetilde{u}_i^n\right\} $如下$ (i=1, 2) $:

(3.10) $ \begin{equation} \widetilde{u}_i^n(a, t)= \left\{\begin{array}{ll} { } \frac{\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}u_{i}^k(a, t){{p}_i^{u^{k}}}(a, t)}} {\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{p}_i^{u^{k}}}(a, t)}}, \quad & { }\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{p}_i^{u^{k}}}(a, t)}\ne 0, \\ 0, \quad &{ }\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{p}_i^{u^{k}}}(a, t)}= 0. \end{array}\right. \end{equation} $

易知$ \widetilde{u}^n=(\widetilde{u}_1^n, \widetilde{u}_2^n)\in {\cal U} $. 空间$ L^2(Q_T) $中有界集的弱紧性意味着: 存在子序列(仍记为$ \{\widetilde{u}^n\} $) 使得

(3.11) $ \begin{eqnarray} \widetilde{u}^n \mathop{\rightarrow }\limits^{\mbox弱} u^*=(u_1^*, u_2^*), \quad n\rightarrow \infty. \end{eqnarray} $

由$ (3.5) $和$ (3.6) $式可导出

(3.12) $ \begin{eqnarray} E(p_i^{u^*})({a, t}) = \alpha_i \int_0^a {p_i^*}( r, t) {\rm d}r + \int_a^{A} p_i^*(r, t){\rm d}r=E(p_i^*)({a, t})\quad {\rm a.e.}\ (a, t)\in Q_T. \end{eqnarray} $

综合$ (2.2) $, $ (3.8) $及$ (3.10) $式, 能推知

(3.13) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial \widetilde{p}_i^n}{\partial t} + \frac{\partial \widetilde{p}_i^n}{\partial a} = -\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{\mu}_{i}}\left( a, {{E}}({{p}_{1}^{u^{k}}})(a, t), {{E}}({{p}_{2}^{u^{k}}})(a, t) \right){p_{i}^{u^{k}}}(a, t)}-\widetilde{u}_i^n (a, t)\widetilde{p}_i^n (a, t), \\ { } \widetilde{p}_i^n(0, t)=\int_{0}^{A}{\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{\beta }_{i}}\left( a, {{E}}({{p}_{i}^{u^{k}}})(a, t) \right){{p}_i^{u^{k}}}(a, t){\rm d}a}}, \\ \widetilde{p}_i^n(a, 0)= p_i^0(a). \end{array} \right. \end{equation} $

如果$ k\ge n+1 $, 那么$ (3.6) $式表明

(3.14) $ \begin{eqnarray} E(p_i^{u^k}) \rightarrow E(p_i^*), \quad n\rightarrow \infty. \end{eqnarray} $

因此, 假设条件$ \rm {(An1)}–{(An3)} $可以保证下列结论成立($ n\rightarrow \infty $)

$ \begin{eqnarray} \left\{\begin{array}{ll} { } \sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}{{\mu}_{i}}\left( a, {{E}}({{p}_{1}^{u^{k}}})(a, t), {{E}}({{p}_{2}^{u^{k}}})(a, t) \right){{p}_i^{u^{k}}}(a, t)}\rightarrow \mu_i(a, E(p_1^*)(a, t), E(p_2^*)(a, t))p_i^*(a, t), \\ { } \sum\limits_{k=n+1}^{{{k}_{n}}}\lambda _{k}^{n}{{{\beta }_{i}}\left( a, {{E}}({{p}_{i}^{u^{k}}})(a, t) \right){{p}_i^{u^{k}}}(a, t)} \rightarrow {{\beta }_{i}}\left( a, {{E}}({{p}_{i}^*})(a, t) \right){{p}^{*}}(a, t). \end{array}\right. \end{eqnarray} $

对方程$ (3.13) $取极限, 即可推知: $ p_i^*=p_i^{u^*}, E(p_i^*)=E(p_i^{u^*}) $.

利用$ (3.4) $式可得

$ d-\frac{1}{n}\le \sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}J(u^{k})}\le d, $

从而

$ \sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}J(u^{k})}\rightarrow d, \quad n\rightarrow \infty. $

另一方面, 由指标泛函定义和控制序列的结构可知

$ \begin{eqnarray} \sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}J(u^{k})}&= &\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}}\sum\limits_{i = 1}^2 {\int_0^A {\int_0^T {{g_i}(a){u_{i}^k}(a, t){p_i^{u^k}}(a, t){\rm{d}}t{\rm{d}}a} } }\\ &=&\sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)\sum\limits_{k=n+1}^{{{k}_{n}}}{\lambda _{k}^{n}}u_{i}^k(a, t)p_{i}^{u^{k}}(a, t){\rm d}t{\rm d}a}}}\\ &=&\sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)\widetilde{u}_i^n (a, t)\widetilde{p}_i^n (a, t){\rm d}t{\rm d}a}}}\\ &\rightarrow &\sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)u^{*}(a, t)p_{i}^{u^{*}}(a, t){\rm d}t{\rm d}a}}} (n\rightarrow \infty)\\ &=&J(u^*). \end{eqnarray} $

这意味着$ J(u^*)=d=\sup\limits_{u\in {\cal U}} J(u) $; 即$ u^* $就是一个最优策略.

本节对最优解作精确刻画. 为此先做一些技术准备.

应用不动点方法不难证明以下结果(细节略去).

引理4.1  给定有界函数$ b_i, \mu_i^2, \mu_i^3, \beta_i^2, (i=1, 2) $, 下列线性系统存在唯一解

(4.1) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial \omega_1}{\partial t} + \frac{\partial \omega_1}{\partial a} =-\mu_1^{2}(a, t)E(\omega_1)(a, t)-\mu_1^{3}(a, t)E(\omega_2)(a, t), \quad({a, t}) \in Q_{T}, \\ { } \frac{\partial \omega_2}{\partial t} + \frac{\partial \omega_2}{\partial a} =-\mu_2^{2}(a, t)E(\omega_2)(a, t)-\mu_2^{3}(a, t)E(\omega_1)(a, t), \quad({a, t}) \in Q_{T}, \\ { } {{\omega }_{i}}(0, t)=\int_{0}^{A}{\beta _{i}^{2}(a, t)E({{\omega }_{i}})(a, t)}{\rm{d}}a+b_{i}(t), \quad t \in(0, T), \\ \omega_i(a, 0) = 0, \quad a \in [0, A]. \end{array} \right. \end{equation} $

类似于引理2.2的证明可得如下结果.

引理4.2  系统$ \rm (4.1) $的解$ w=(w_1, w_2)\in [L^{\infty}(Q_T)]^2 $连续依赖于$ b=(b_{1}, b_2)\in [L^{\infty}(0, T)]^2 $.

以下证明一个新的连续性结果, 它在刻画最优策略的过程中起关键作用.

引理4.3  令函数$ f_i^n, \mu_i^k, \beta_i^k, b_i^n $有界, 记$ \omega^n=(\omega_1^{n}, \omega_2^{n}) $为下列系统的解

(4.2) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial \omega_1}{\partial t} + \frac{\partial \omega_1}{\partial a} =f_{1}^n(a, t)-\mu_1^{1}(a, t)\omega_1(a, t)-\mu_1^{2}(a, t)E(\omega_1)(a, t)-\mu_1^3(a, t)E(\omega_2)(a, t), \\ { } \frac{\partial \omega_2}{\partial t} + \frac{\partial \omega_2}{\partial a} =f_{2}^n(a, t)-\mu_2^{1}(a, t)\omega_2(a, t)-\mu_2^{2}(a, t)E(\omega_2)(a, t)-\mu_2^{3}(a, t)E(\omega_1)(a, t), \\ { } {{\omega }_{i}}(0, t)=\int_{0}^{A}{\left[ \beta _{i}^{1}(a, t){{\omega }_{i}}(a, t)+\beta _{i}^{2}(a, t)E({{\omega }_{i}})(a, t) \right]}{\rm{d}}a+b_{i}^n(t), \\ \omega_i(a, 0) = \omega_i^0(a), \quad({a, t}) \in Q_{T}, i=1, 2. \end{array} \right. \end{equation} $

若$ (f_i^{n}, b_{i}^n)\rightarrow (f_i, b_i) $, $ n\rightarrow \infty $, 则$ \omega^n\rightarrow \omega $, 其中$ \omega=(\omega_1, \omega_2) $是系统$ (4.2) $相应于$ f_{i}^n=f_i, b_{i}^n=b_i (i=1, 2) $的解.

证  系统$ (4.2) $可以分解成下列两个子系统

(4.3) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial \omega_1^1}{\partial t} + \frac{\partial \omega_1^1}{\partial a} =f_1^{n}(a, t)-\mu_1^{1}(a, t)\omega_1^1(a, t), \\ { } \frac{\partial \omega_2^1}{\partial t} + \frac{\partial \omega_2^1}{\partial a} =f_2^{n}(a, t)-\mu_2^{1}(a, t)\omega_2^1(a, t), \\ { } {{\omega }_{i}}^1(0, t)=\int_{0}^{A}{\beta _{i}^{1}(a, t){{\omega }_{i}}^1(a, t)}{\rm{d}}a, \quad t \in(0, T), \\ \omega_i^1(a, 0) = \omega_i^0(a), \quad({a, t}) \in Q_{T}, i=1, 2, \end{array} \right. \end{equation} $

(4.4) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{\partial \omega_1^2}{\partial t} + \frac{\partial \omega_1^2}{\partial a} =-\mu_1^{2}(a, t)E(\omega_1^2)(a, t)-\mu_1^{3}(a, t)E(\omega_2^2)(a, t), \\ { } \frac{\partial \omega_2^2}{\partial t} + \frac{\partial \omega_2^2}{\partial a} =-\mu_2^{2}(a, t)E(\omega_2^2)(a, t)-\mu_2^{3}(a, t)E(\omega_1^2)(a, t), \\ { } {{\omega }_{i}}^2(0, t)=\int_{0}^{A}{\beta _{i}^{2}(a, t)E({{\omega }_{i}}^2)(a, t)}{\rm{d}}a+b_i^{n}(t), \\ \omega_i^2(a, 0) = 0, \quad({a, t}) \in Q_{T}, i=1, 2. \end{array} \right. \end{equation} $

记系统$ (3.3) $的解为$ \omega^{1n}=(\omega_{1}^{1n}, \omega_2^{1n}) $. 利用一个已知结果^{[2, p24, Theorem 2.1.2(iii)]}可得: 若$ f_i^{n}\rightarrow f_i $, $ n\rightarrow \infty $, 则$ \omega^{1n}\rightarrow \omega^1=(\omega_1^1, \omega_2^1) $, 其中$ \omega_i^1 $是系统$ (4.3) $相应于$ f_i^{n}=f_i $的解.

令$ \omega^{2n}=(\omega_{1}^{2n}, \omega_2^{2n}) $为系统(4.4)的解. 引理4.1和4.2表明$ \omega^{2n} $已经适定且关于$ b^n $连续.

以下证明本节的主要结果.

定理4.1(最大值原理)  记

$ u^*=(u_1^*, u_2^*), {\quad} p^*=(p_1^*, p_2^*). $

如果$ (u^*, p^*) $是控制问题(2.1)–(2.2) 的最优对, $ q=(q_1, q_2) $满足以下共轭系统($ i, j=1, 2; $$ i\neq j $)

(4.5) $ \begin{equation} \left\{\begin{array}{ll} { } \quad \frac{\partial q_i}{\partial t} + \frac{\partial q_i}{\partial a}\\ { } =\alpha_i\int_a^A\left[\mu _{ix}(r, E(p_1^*)(r, t), E(p_2^*)(r, t))q_i(r, t)-\beta_{ix}(r, E(p_i^*)(r, t))q_i(0, t)\right]p_i^*(r, t){\rm{d}}r\\ { } \quad+\int_0^a\left[\mu _{ix}(r, E(p_1^*)(r, t), E(p_2^*)(r, t))q_i(r, t)-\beta_{ix}(r, E(p_i^*)(r, t))q_i(0, t)\right]p_i^*(r, t){\rm d}r\\ { } \quad+\alpha_i\int_a^A \mu_{jx}(r, E(p_1^*)(r, t), E(p_2^*)(r, t))q_j(r, t)p_j^*(r, t){\rm d}r\\ { } \quad+\int_0^a \mu_{jx}(r, E(p_1^*)(r, t), E(p_2^*)(r, t))q_j(r, t)p_j^*(r, t){\rm d}r\\ { } \quad+[g_i(a)+q_i(a, t)]u_i^*(a, t) -\beta_i(a, E(p_i^*)(a, t))q_i(0, t)\\ { } \quad+\mu_i(a, E(p_1^*)(a, t), E(p_2^*)(a, t))q_i(a, t), (a, t)\in [0, A)\times [0, T), \\ { } q_i(a, T)=0, q_i(A, t)=0, \quad({a, t}) \in Q_{T}, i=1, 2, \end{array}\right. \end{equation} $

那么最优策略$ u_i^* $必定具有如下结构

(4.6) $ \begin{equation} u_i^*(a, t)= \left\{\begin{array}{ll} 0, &\mbox{if}\ g_i(a)+q_i(a, t)<0; \\ U_i, &\mbox{if}\ g_i(a)+q_i(a, t)>0. \end{array}\right. \end{equation} $

证  对于任意切向量$ v=(v_1, v_2)\in {\cal T}_{\cal U}(u^*) $ (集$ {\cal U} $在$ u^* $处的切锥), $ \varepsilon>0 $充分小时必有$ u^\varepsilon :=u^*+\varepsilon v\in {\cal U} $ (参见文献[33, p21, Proposition 2.3]). 由$ u^* $的最优性知$ J(u^\varepsilon)\le J(u^*) $; 此即

(4.7) $ \begin{eqnarray} && \sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)[u_{i}^{*}(a, t)+\varepsilon {{v}_{i}}(a, t)]p_{i}^{\varepsilon }(a, t){\rm d}t{\rm d}a}}} {}\\ &\le &\sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)u_{i}^{*}(a, t)p_{i}^*(a, t){\rm d}t{\rm d}a}}}, \end{eqnarray} $

其中$ p^\varepsilon=(p_1^\varepsilon, p_2^\varepsilon) $为系统$ (2.2) $相应于$ u=u^\varepsilon $的解. 将$ (4.7) $式同除以$ \varepsilon $并取极限$ \varepsilon\rightarrow 0^+ $, 可得

(4.8) $ \begin{equation} \sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{{{g}_{i}}(a)[u_{i}^{*}(a, t){{z}_{i}}(a, t)+p_{i}^{*}(a, t){{v}_{i}}(a, t)]{\rm d}t{\rm d}a}}}\le 0, \end{equation} $

其中$ z_i(a, t)=\lim\limits_{\varepsilon \to {{0}^{+}}} \frac{p_{i}^{\varepsilon }(a, t)-p_{i}^{*}(a, t)}{\varepsilon } (i=1, 2) $由下列方程决定($ i, j=1, 2; i\neq j $)

(4.9) $ \begin{equation} \left\{\begin{array}{ll} { } \frac{\partial z_i}{\partial t} + \frac{\partial z_i}{\partial a}=-\left[\mu_{ix}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E(z_i)(a, t)\right.\\ {\quad} \quad\quad\quad\quad\quad +\mu_{iy}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E(z_j)(a, t)+v_i(a, t)\big]p_i^*(a, t)\\ {\quad} \quad\quad\quad\quad\quad -\left[u_i^*(a, t)+\mu_i(a, E(p_1^*)(a, t), E(p_2^*)(a, t))\right]z_i(a, t), \\ { } z_i(0, t)=\int_0^A\left[\beta_{ix}(a, E(p_i^*)(a, t))p_i^*(a, t)E(z_i)(a, t)+\beta_i(a, E(p_i^*)(a, t))z_i(a, t)\right]{\rm d}a, \\ z_i(a, 0)=0, \quad (a, t)\in Q_T, i=1, 2, \end{array}\right. \end{equation} $

上述系统中的$ \mu_{ix} $和$ \mu_{iy} $分别表示$ \mu_i $对第二和第三个变量的偏导数.

首先证明$ \lim\limits_{\varepsilon \to {{0}^{+}}} \frac{p_{i}^{\varepsilon }(a, t)-p_{i}^{*}(a, t)}{\varepsilon } $存在. 注意方程$ (4.9) $是线性的, 其解的存在唯一性可用不动点方法建立, 此处略去细节.

记

$ \omega_i^\varepsilon(a, t)=\frac{1}{\varepsilon }\left[{p_{i}^{\varepsilon }(a, t)-p_{i}^{*}(a, t)}\right]-z_i(a, t). $

利用方程$ (2.2) $经计算可得

(4.10) $ \begin{equation} \left\{\begin{array}{ll} { } \frac{\partial \omega_i^\varepsilon}{\partial t} + \frac{\partial \omega_i^\varepsilon}{\partial a}=-\mu_{ix}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E\left(\frac{1}{\varepsilon }\left[{p_{1}^{\varepsilon }-p_{1}^{*}}\right]\right)(a, t)p_i^\varepsilon(a, t)\\ { } {\quad} \ \quad\quad\quad\quad\quad -\mu_{iy}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E\left(\frac{1}{\varepsilon }\left[{p_{2}^{\varepsilon }-p_{2}^{*}}\right]\right)(a, t)p_i^\varepsilon(a, t)\\ \ {\quad} \quad\quad\quad\quad\quad -\omega_i^\varepsilon(a, t)\left[u_i^*(a, t)+\mu_i(a, E(p_1^*)(a, t), E(p_2^*)(a, t))\right]\\ {\quad} \ \quad\quad\quad\quad\quad +\mu_{ix}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E(z_1)(a, t)p_i^*(a, t)\\ {\quad} \ \quad\quad\quad\quad\quad +\mu_{iy}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E(z_2)(a, t)p_i^*(a, t)\\ {\quad} \ \quad\quad\quad\quad\quad -v_i(a, t)\left[p_i^\varepsilon(a, t)-p_i^*(a, t)\right], \\ { } \omega_i^\varepsilon(0, t)=\int_0^A\beta_{ix}(a, E(p_i^*)(a, t))p_i^\varepsilon(a, t)E\left(\frac{1}{\varepsilon }\left[{p_{i}^{\varepsilon }-p_{i}^{*}}\right]\right)(a, t){\rm d}a\\ { } \quad\quad\quad\quad \ -\int_0^A\beta_{ix}(a, E(p_i^*)(a, t))p_i^*(a, t)E(z_i)(a, t){\rm d}a\\ { }\quad\quad\quad\quad\ +\int_0^A\beta_i(a, E(p_i^*)(a, t))\omega_i^\varepsilon(a, t){\rm d}a+b_i^0(\varepsilon), \\ \omega_i^\varepsilon(a, 0)=0, \quad (a, t)\in Q_T, i=1, 2, \end{array}\right. \end{equation} $

其中$ b_i^0(\varepsilon)\rightarrow 0 $ ($ \varepsilon\rightarrow 0^+ $).

引理2.2意味着

$ {p_{i}^{\varepsilon }(a, t)-p_{i}^{*}}(a, t)\rightarrow 0, \quad {\rm a.e.}\ (a, t)\in Q_T, \varepsilon\rightarrow 0^+, $

$ \begin{eqnarray} \left| E\left( \frac{1}{\varepsilon}[p_i^{\varepsilon}-p_i^*]\right)(a, t) \right| &\le& \int_0^A |p_i^{\varepsilon}(r, t)-p_i^{*}(r, t)|{\rm d}r\\ &\le & A \|p_i^{\varepsilon}-p_i^* \|_{L^{\infty}(Q_T)}\\ &\le& AC{\varepsilon}\|v_i\|_{L^{\infty}(Q_T)}, \end{eqnarray} $

因此, 系统($ 4.10 $) 的极限系统如下

(4.11) $ \begin{equation} \left\{\begin{array}{ll} { } \frac{\partial \omega_i}{\partial t} + \frac{\partial \omega_i}{\partial a}=-\omega_i(a, t)\left[u_i^*(a, t)+\mu_i(a, E(p_1^*)(a, t), E(p_2^*)(a, t))\right]\\ {\quad} \quad\quad\quad\quad\quad -\mu_{ix}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E\left(\omega_1\right)(a, t)p_i^*(a, t)\\ {\quad} \quad\quad\quad\quad\quad -\mu_{iy}(a, E(p_1^*)(a, t), E(p_2^*)(a, t))E\left(\omega_2\right)(a, t)p_i^*(a, t), \\ { } \omega_i(0, t)=\int_0^A\beta_{ix}(a, E(p_i^*)(a, t))p_i^*(a, t)E\left(\omega_i\right)(a, t){\rm d}a \\ { } \ \quad\quad\quad\quad +\int_0^A\beta_i(a, E(p_i^*)(a, t))\omega_i(a, t){\rm d}a, \\ \omega_i(a, 0)=0, \quad (a, t)\in Q_T, i=1, 2. \end{array}\right. \end{equation} $

对于给定的$ (u^*, p^*) $, 系统($ 4.11 $) 为齐次线性且具有零初始条件, 其唯一解必定恒为零; 即$ \omega_i(a, t)\equiv 0 $. 由引理4.3知: $ \lim\limits_{\varepsilon \to {{0}^{+}}} \omega _{i}^{\varepsilon }=0 $; 此即下列极限

$ z_i(a, t)=\lim\limits_{\varepsilon \to {{0}^{+}}} \frac{p_{i}^{\varepsilon }(a, t)-p_{i}^{*}(a, t)}{\varepsilon }, {\quad} i=1, 2 $

存在, 且为系统$ (4.9) $的解.

对系统$ (4.9) $的第一个方程乘以$ q_i(a, t) $并在$ Q_T $上积分, 计算并利用系统$ (4.5) $可得

(4.12) $ \begin{equation} \sum\limits_{i=1}^{2}\int_{0}^{A}\int_{0}^{T}g_i(a)u_i^*(a, t)z_i(a, t){\rm d}t{\rm d}a=\sum\limits_{i=1}^{2}\int_{0}^{A} \int_{0}^{T}q_i(a, t)p_{i}^{*}(a, t)v_i(a, t){\rm d}t{\rm d}a. \end{equation} $

将$ (4.12) $式代入$ (4.8) $式可知: 不等式

$ \sum\limits_{i=1}^{2}{\int_{0}^{A}{\int_{0}^{T}{[{{g}_{i}}(a)+q_{i}(a, t)]p_i^*(a, t){{v}_{i}}(a, t){\rm d}t{\rm d}a}}}\le 0 $

对于任意$ v_i\in {\cal T}_{{\cal U}_i}(u_i^*) $均成立. 法锥的定义意味着

$ (g_i+q_i)p_i^*\in {\cal N}_{{\cal U}_i}(u_i^*), {\quad} i=1, 2, $

其中$ {\cal N}_{{\cal U}_i}(u_i^*) $表示集$ {\cal U}_i $在$ u_i^* $处的法锥. 再运用法向量的结构特征即可推出定理4.1的结论.

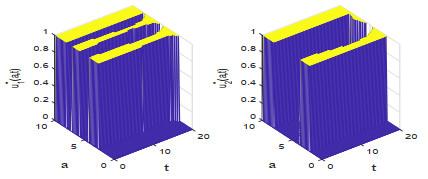
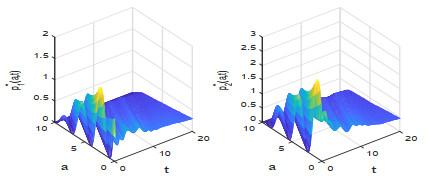
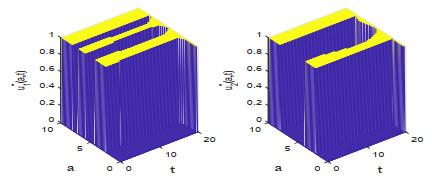
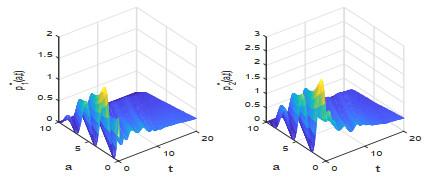
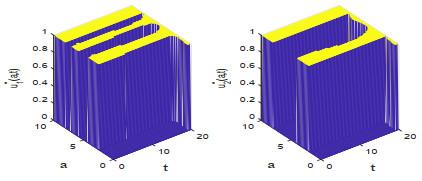
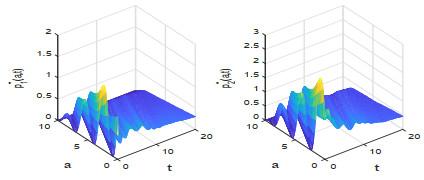
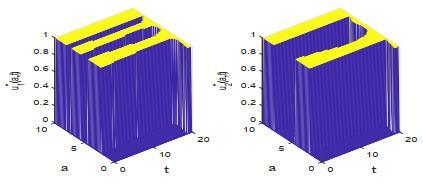
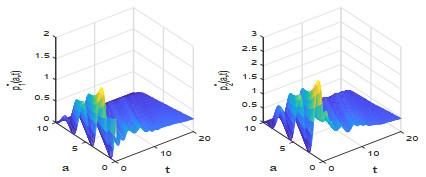
本节根据定理4.1对控制问题(2.1)–(2.2) 做数值求解, 并观察最优收益随价格函数的变化情况.

例5.1  选取参数$ \alpha_1=0.4, \alpha_2=0.3, A=10, T=20 $;

$ p_1^0(a)=0.2(10-a)\cos^2\Big(a+\frac{\pi}{4}\Big), {\quad} p_2^0(a)=0.3(10-a)\sin^2\Big(a+\frac{\pi}{4}\Big) ; $

初始控制为

$ u_1^0(a, t)=u_2^0(a, t)= \left\{ \begin{array}{ll} 0, &\quad t\le -2a+10, \\ 1, &\quad t>-2a+10; \end{array} \right. $

死亡率

$ \mu_1(a, x_1, x_2)= \left\{ \begin{array}{ll} { } 0.06\cos^2(4a)+0.03{x_1}+0.02{x_2}+\frac{2-a}{50}, &\quad 0\le a<2; \\ 0.06\cos^2(4a)+0.03{x_1}+0.02{x_2}, &\quad 2\le a<8; \\ { } 0.06\cos^2(4a)+0.03{x_1}+0.02{x_2}+\frac{a-8}{10-a}, &\quad 8\le a<10; \end{array} \right. $

$ \mu_2(a, x_1, x_2)= \left\{ \begin{array}{ll} { } 0.04\cos^2(4a)+0.02{x_1}+0.03{x_2}+\frac{2-a}{50}, &\quad0\le a<2; \\ 0.04\cos^2(4a)+0.02{x_1}+0.03{x_2}, &\quad2\le a<8; \\ { } 0.04\cos^2(4a)+0.02{x_1}+0.03{x_2}+\frac{a-8}{10-a}, &\quad 8\le a<10; \end{array} \right. $

繁殖率

$ \beta_1(a, x_1)= \left\{ \begin{array}{ll} 0.02(\cos(a)+1)+0.96(2-a), &\quad 1\le a<2; \\ 0.02(\cos(a)+1), &\quad 2\le a<8; \\ 0.02(\cos(a)+1)+0.96(a-8), &\quad 8\le a<9; \\ 0, &\quad \mbox{其它}; \end{array} \right. $

$ \beta_2(a, x_2)= \left\{ \begin{array}{ll} 0.01(\sin(a)+1)+0.98(2-a), &\quad1\le a<2; \\ 0.01(\sin(a)+1), &\quad 2\le a<8; \\ 0.01(\sin(a)+1)+0.98(a-8), &\quad 8\le a<9; \\ 0, &\quad \mbox{其它}; \end{array} \right. $

价格函数($ s $为可变参数):

$ g_1(a)= \left\{ \begin{array}{ll} 0.05s, &\quad 0\le a<2; \\ 0.2(1+\cos(2a))+0.05s, &\quad 2\le a<8; \\ 0.5+0.05s, &\quad 8\le a<10; \end{array} \right. $

$ g_2(a)= \left\{ \begin{array}{ll} 0.05s, &\quad 0\le a<2; \\ 0.2(1+\sin(a))+0.05s, &\quad 2\le a<8; \\ 1+0.05s, &\quad 8\le a<10. \end{array} \right. $

对于四种参数值$ s=0, 1, 2, 3 $, 分别计算最优收获强度$ (u_1^* (a, t), u_2^* (a, t)) $, 最优种群密度$ (p_1^* (a, t), p_2^* (a, t)) $以及最优收益$ J(u^*) $, 利用计算数据绘制图 1 –图 8, 以及表 1.

对基于种群系统($ 2.2 $) 的最优收益问题($ 2.1 $), 定理3.1断言它至少有一个最优解, 定理4.1则给出了最优策略的特征结构. 为了获得具体的最优策略, 必须综合运用状态系统($ 2.2 $) 和共轭方程($ 4.5 $). 因此, 最优策略是一种反馈形式, 基本上具有Bang-Bang结构. 定理4.1为逼近最优策略、最优密度函数和最优收益奠定了基础.

需要强调的是: 尽管表 1中的数据显示最优收益随着价格的上升而增加, 但数据来源于近似计算, 普遍的规律尚不清楚, 因为最优收益由($ 2.1 $)–($ 2.2 $) 式和($ 4.6 $) 式决定, 这是一个复杂的耦合约束控制问题, 难以从理论上发现收益随价格的变化趋势.