考虑无约束优化问题

(1.1) $ \begin{eqnarray} \min\limits_{x\in{{\mathbb{R}}} ^n}\ \ f(x), \end{eqnarray} $

其中$ f:{{\mathbb{R}}} ^n\rightarrow {{\mathbb{R}}} $是连续可微函数. 由于共轭梯度法每步迭代不需要矩阵存储, 且具有良好的收敛性质, 是求解大规模光滑无约束优化问题(1.1)最有效的数值方法之一. 共轭梯度法迭代点列通常由以下公式产生

$ \begin{eqnarray} x_{k+1}&=&x_{k}+\alpha_{k}d_{k}, \\ d_k&=&\left\{\begin{array}{ll}-g_k, &k=1, \\-g_k+\beta_k d_{k-1}, &k\geq2. \end{array}\right. \end{eqnarray} $

其中$ g_{k}=\nabla f(x_{k}) $为当前迭代点的梯度, $ \beta_k\in{{\mathbb{R}}} $为共轭参数, $ \alpha_k $为步长.

共轭参数$ \beta_k $的选取对共轭梯度法的收敛性以及数值表现至关重要. 经典共轭梯度法包括Hestenes-Stiefel(HS)方法^[1], Fletcher-Reeves(FR)方法^[2], Polak-Ribière-Polak(PRP) 方法^{[3, 4]}, Dai-Yuan(DY)方法^[5], Fletcher (CD)方法^[6]和Liu-Storey(LS)方法^[7]. 其中PRP方法是数值表现较好的经典共轭梯度法之一, 其共轭参数计算公式为

$ \beta_k^{\rm PRP}=\frac{g_k^T(g_k-g_{k-1})}{\|g_{k-1}\|^2}. $

PRP方法自带重启功能, 即算法在迭代过程中一旦出现小步长, 下一步迭代即以最速下降方向进行重启, 从而有效避免算法连续产生小步长, 进而提高算法计算效率. PRP方法这个性质的严格表述最早见文献[8], 并称之为性质($ \ast $). 然而, 在常规假设和非精确线搜索条件下, PRP方法并不具备FR方法和DY方法良好的收敛性. Powell^[9]的研究表明, PRP方法对于一般的非凸函数, 即使在精确线搜索条件下也无法保证它的全局收敛性. 特别地, 当$ \beta_k^{\rm PRP}<0 $且$ \|d_{k-1}\| $很大时, 算法相邻的两个方向会趋于反向. 于是, Powell^[10]建议对$ \beta_k^{\rm PRP} $进行非负化, 即$ \beta_k^{\rm PRP+}=\max\{0, \beta_k^{\rm PRP}\} $, 由此产生的方法称为PRP+ 方法. PRP+ 方法的数值表现优于PRP方法. 但是, 对一般的目标函数, 采用非精确线搜索准则求步长仍无法保证由PRP+方法产生的搜索方向满足下降条件, 从而无法保证PRP+方法全局收敛. 为此, Gilbert和Nocedal^[8]在算法满足Wolfe线搜索和充分下降条件的假设下, 证明了PRP+ 方法对一般非凸函数的全局收敛性.

鉴于PRP方法以上理论和数值性质, 许多学者围绕PRP方法改进进行深入研究, 近期部分代表性成果见文献[11-18]. 如基于共轭参数公式修正PRP方法^[11], 杂交PRP方法^[12], 谱PRP方法^[13-16], 三项PRP方法^[17]和谱三项PRP方法^[18].

本文继续研究PRP方法的改进, 目的是建立结构简单、计算效率高、收敛性好的PRP型谱共轭梯度法. 全文余下部分安排如下: 第2部分结合Wolfe线搜索准则对PRP公式进行改进, 并基于新共轭参数设计新的谱参数, 引入重启条件并构造新的重启方向, 建立新算法; 第3部分证明算法的下降性和全局收敛性; 第4部分对算法进行中大规模数值实验并分析报告测试结果.

本节最后给出本文用于产生步长的线搜索准则—强Wolfe线搜索准则, 即

(1.2) $ \begin{eqnarray} \left\{\begin{array}{ll}f(x_k+\alpha_k d_k)\leq f(x_k)+\delta\alpha_k g_k^Td_k, \\-\sigma |g_k^Td_k|\leq g(x_k+\alpha_k d_k)^T d_k\leq\sigma |g_k^Td_k|, \end{array}\right. \end{eqnarray} $

其中$ 0<\delta<\sigma<1. $

Dai和Yuan^[19]提出一类单参数共轭梯度法簇, 其共轭参数为

$ \beta_k=\frac{\|g_k\|^{2}}{\lambda\|g_{k-1}\|^{2}+(1-\lambda)d_{k-1}^T(g_k-g_{k-1})}. $

显然, 当$ \lambda=1 $, $ 0 $时, 上式分别对应为FR公式和DY公式. 当$ \lambda=\frac{1}{2} $时, 上式变为

(2.1) $ \begin{eqnarray} \beta_k=\frac{2\|g_k\|^{2}}{\|g_{k-1}\|^{2}+d_{k-1}^T(g_k-g_{k-1})}. \end{eqnarray} $

受(2.1)式分母结构的启发, 结合强Wolfe线搜索准则(1.2), 本文考虑将PRP公式改进为

(2.2) $ \begin{eqnarray} \beta_k^{\rm JLJW}=\frac{g_k^T(g_k-g_{k-1})}{\|g_{k-1}\|^{2}+d_{k-1}^T(g_k-\sigma g_{k-1})}. \end{eqnarray} $

显然, 当$ g_{k-1}^Td_{k-1}<0 $时, 由(1.2)第二式左边易知$ d_{k-1}^T(g_k-\sigma g_{k-1})>0 $, 于是有$ |\beta_k^{\rm JLJW}|\leq|\beta_k^{\rm PRP}| $, 称与(2.2)式相应的共轭梯度法为JLJW方法. 通过大量数值实验(见第4部分), 发现JLJW方法的数值表现优于PRP方法、HS方法和LS方法. 然而, 在常规假设和非精确线搜索条件下, 对一般函数, JLJW方法跟PRP方法一样难以收敛. 因此, 为了保证JLJW方法全局收敛, 须对JLJW方法作进一步改进.

谱思想较早出现在Barzilai和Borwein^[20]提出的两点步长梯度法(简称BB方法)中, 其每步线搜索仅使用负梯度方向, 即

$ d_k=-\theta_{k}g_k, \ \ \ \ \theta_{k}=\frac{s_{k-1}^Ts_{k-1}}{s_{k-1}^Ty_{k-1}}, \ \ \ \ s_{k-1}=x_k-x_{k-1}, \ \ y_{k-1}=g_k-g_{k-1}. $

数值结果表明, 对于许多无约束优化问题BB方法明显优于最速下降法. 基于文献[20], Luengo等在文献[21]结合预处理技术提出了预条件谱梯度法, 其数值实验结果表明该方法优于一些复杂的共轭梯度法. Birgin和Martinez^[22]将谱梯度法与共轭梯度法相结合提出谱共轭梯度法, 其搜索方向为

(2.3) $ \begin{eqnarray} d_k=\left\{\begin{array}{ll}-g_k, &k=1, \\-\theta_kg_k+\beta_kd_{k-1}, &k\geq2. \end{array}\right. \end{eqnarray} $

由(2.3)式不难发现, 若$ \theta_k=1 $, 谱共轭梯度法退化为经典共轭梯度法, 若$ \theta_k>1 $, 相比于二项共轭梯度法, 谱共轭梯度法每步迭代均有较大下降量. 受Birgin和Martinez工作的启发, 文献[16] 提出一个修正的谱PRP方法, 其搜索方向为

$ d_k=\left\{\begin{array}{ll}-g_k, &k=1, \\-\theta_{k}g_k+\beta_k^{\rm DPRP}d_{k-1}, &k\geq2. \end{array}\right. $

谱参数$ \theta_{k} $由条件$ g_{k}^Td_k=-\|g_k\|^2 $求得, 即为

$ \theta_{k}=1+\beta_k^{\rm DPRP}\frac{g_k^Td_{k-1}}{\|g_k\|^2}, \ \ \ \ \beta_k^{\rm DPRP}=\frac{g_k^T(g_k-g_{k-1})}{\|g_{k-1}\|^{2}}-\mu\frac{\|g_k-g_{k-1}\|^2g_k^Td_{k-1}}{\|g_{k-1}\|^4} \qquad(\mu\geq\frac{1}{4}). $

另一方面, Kou和Dai^[23]提出一个带新型重启方向的改进三项共轭梯度法(简称KD方法), 其重启方向为

(2.4) $ \begin{eqnarray} d_k=-g_k+\eta\frac{g_k^Td_{k-1}}{\|d_{k-1}\|^2}d_{k-1}. \end{eqnarray} $

由于新型重启方向的引入, 使得KD方法具有良好的理论性质和数值表现. 受文献[16, 23]的启发, 为确保JLJW方法全局收敛和提高其计算效率, 我们对JLJW方法引入新的谱参数和重启方向, 构造搜索方向如下

(2.5) $ \begin{eqnarray} d_k=\left\{\begin{array}{ll} -g_k, &k=1, \\ -\theta_{k}g_k+\beta_k^{\rm JLJW} d_{k-1}, &k\geq2, \ \mbox{且}\ \ 0\leq g_{k}^Tg_{k-1}\leq r\|g_{k}\|^{2}, \\ { } -\tilde{\theta_{k}}g_{k}+\eta\frac{g_{k}^Td_{k-1}}{\|d_{k-1}\|^{2}}d_{k-1}, &\mbox{其他}. \end{array}\right. \end{eqnarray} $

其中$ 0<r\leq1, $

$ \theta_{k}=1+\beta_k^{\rm JLJW}\frac{|g_k^Td_{k-1}|}{\|g_k\|^2}, \ \ \tilde{\theta_{k}}=1+\eta\frac{(g_{k}^Td_{k-1})^2}{\|d_{k-1}\|^{2}\|g_k\|^2}\ \ (0\leq\eta<1). $

当$ 0\leq g_{k}^Tg_{k-1}\leq r\|g_{k}\|^{2} $且$ g_{k-1}^Td_{k-1}<0 $时, 由(1.2)式可得$ 0\leq\beta_k^{\rm JLJW} $. 因此, (2.5)式中$ \theta_{k}\geq 1. $显然, $ \tilde{\theta_{k}}\geq 1. $当$ \eta=0 $时, 由(2.5)式知: 重启方向$ d_k=-g_k, $即为标准的最速下降方向.

基于搜索方向(2.5)及强Wolfe线搜索准则(1.2), 下面给出本文的算法步骤(简记为$ \rm JLJW^{+} $算法).

初始步  任取初始点$ x_1\in {{\mathbb{R}}} ^n $, 参数$ 0<\delta<\sigma<1, 0<r\leq1, 0\leq\eta<1 $. 给定终止精度$ \epsilon>0 $. $ d_1=-g_1 $, 置$ k:=1 $.

步骤1  若$ \|g_k\|\leq \epsilon $, 则停止. 否则, 转入步骤2.

步骤2  采用强Wolfe线搜索条件(1.2)计算步长$ \alpha_k $.

步骤3  按$ x_{k+1}=x_k+\alpha_kd_k $产生新的迭代点, 计算$ g_{k+1}:=g(x_{k+1}) $, 并由(2.2)及(2.5)式计算搜索方向$ d_{k+1} $.

步骤4  令$ k:=k+1 $, 返回步骤1.

为了获得$ \rm JLJW^{+} $算法的充分下降性和收敛性, 首先给出下面关于目标函数的两个基本假设.

(H1) 目标函数$ f(x) $在水平集$ \Lambda=\{x\in {{\mathbb{R}}} ^n\ | \ f(x)\leq f(x_1)\} $上有下界, 其中$ x_{1} $为算法的初始点;

(H2) 目标函数$ f(x) $在水平集$ \Lambda $的一个邻域$ {\rm U} $内可微, 且其梯度函数$ g(x) $满足$ \rm Lipschitz $条件, 即存在$ L>0 $, 使得$ \|g(x)-g(y)\|\leq L\|x-y\|, \forall\ x, y\in U. $

以下引理表明, 在强Wolf线搜索条件下, $ \rm JLJW^{+} $算法的搜索方向具有充分下降性.

引理3.1  算法$ \rm JLJW^{+} $的搜索方向$ d_k $满足

(3.1) $ \begin{eqnarray} -\frac{1}{1-2\sigma}\leq\frac{g_{k}^Td_{k}}{\|g_{k}\|^{2}}\leq -1\quad (0<\sigma<\frac{1}{2}) \end{eqnarray} $

对$ \forall k\geq1 $成立.

证  当$ k=1 $时, $ g_1^Td_1=-\|g_1\|^2 $, 此时(3.1)式成立. 假设对$ k-1 $的情形(3.1)式成立, 下面分两种情形证明其对$ k\geq2 $的情形也成立.

(i) 当搜索方向$ d_k $为重启方向, 即$ d_k=-\tilde{\theta_k}g_{k}+\eta\frac{g_{k}^Td_{k-1}}{\|d_{k-1}\|^{2}}d_{k-1} $时, 有

(3.2) $ \begin{eqnarray} \frac{g_{k}^Td_{k}}{\|g_k\|^{2}}&=&\frac{-(1+\eta\frac{(g_{k}^Td_{k-1})^2}{\|d_{k-1}\|^{2}\|g_k\|^{2}})\|g_k\|^{2} +\eta\frac{g_k^Td_{k-1}}{\|d_{k-1}\|^{2}}g_k^Td_{k-1}}{\|g_k\|^{2}} \\ &=&-(1+\eta\frac{(g_{k}^Td_{k-1})^2}{\|d_{k-1}\|^{2}\|g_k\|^{2}}) +\eta\frac{(g_{k}^Td_{k-1})^2}{\|d_{k-1}\|^{2}\|g_k\|^{2}} \\ &=&-1. \end{eqnarray} $

(ii) 当$ 0\leq g_{k}^Tg_{k-1}\leq r\|g_{k}\|^{2} $时, 搜索方向$ d_k=-\theta_kg_k+\beta_k^{\rm JLJW} d_{k-1} $. 于是有

(3.3) $ \begin{eqnarray} g_{k}^Td_{k}&=&-(1+\beta_k^{\rm JLJW}\frac{|g_{k}^Td_{k-1}|}{\|g_k\|^{2}})\|g_k\|^{2}+\beta_k^{\rm JLJW}g_{k}^Td_{k-1}\\ &=&-\|g_k\|^{2}-\beta_k^{\rm JLJW}|g_{k}^Td_{k-1}|+\beta_k^{\rm JLJW}g_{k}^Td_{k-1}. \end{eqnarray} $

若$ g_{k}^Td_{k-1}\geq0 $, 则由(3.3)式有

(3.4) $ \begin{eqnarray} g_{k}^Td_{k}=-\|g_k\|^{2}. \end{eqnarray} $

若$ g_{k}^Td_{k-1}<0 $, 则由(3.3)式有

(3.5) $ \begin{eqnarray} g_{k}^Td_{k}=-\|g_k\|^{2}+2\beta_k^{\rm JLJW}g_{k}^Td_{k-1}. \end{eqnarray} $

由归纳假设, 可知$ g_{k-1}^Td_{k-1}<0 $; 另外, 由(1.2)式可知$ \sigma g_{k-1}^Td_{k-1}\leq g_{k}^Td_{k-1}, $再根据(2.2)式可得

(3.6) $ \begin{eqnarray} 0\leq\beta_k^{\rm JLJW}=\frac{\|g_{k}\|^{2}-g_k^Tg_{k-1}}{\|g_{k-1}\|^{2}+d_{k-1}^T(g_k-\sigma g_{k-1})}\leq \frac{\|g_k\|^2}{\|g_{k-1}\|^2}. \end{eqnarray} $

结合(3.5)和(3.6)式可得

(3.7) $ \begin{eqnarray} -\|g_k\|^{2}+2\frac{\|g_k\|^2}{\|g_{k-1}\|^2}\sigma g_{k-1}^Td_{k-1}\leq -\|g_k\|^{2}+2\frac{\|g_k\|^2}{\|g_{k-1}\|^2}g_k^Td_{k-1}\leq g_{k}^Td_{k}\leq -\|g_k\|^{2}. \end{eqnarray} $

根据(3.4)和(3.7)式可知, 搜索方向$ d_k=-\theta_kg_k+\beta_k^{\rm JLJW} d_{k-1} $总满足

$ -\|g_k\|^{2}+2\frac{\|g_k\|^2}{\|g_{k-1}\|^2}\sigma g_{k-1}^Td_{k-1}\leq g_{k}^Td_{k}\leq -\|g_k\|^{2}. $

将上式两边同时除以$ \|g_k\|^2 $可得

$ \begin{eqnarray} -1+2\sigma\frac{g_{k-1}^Td_{k-1}}{\|g_{k-1}\|^2}\leq\frac{g_{k}^Td_{k}}{\|g_{k}\|^{2}}\leq -1. \end{eqnarray} $

此结合归纳假设$ -\frac{1}{1-2\sigma}\leq\frac{g_{k-1}^Td_{k-1}}{\|g_{k-1}\|^{2}} $, 得

(3.8) $ \begin{eqnarray} -\frac{1}{1-2\sigma}=-1-2\frac{\sigma}{1-2\sigma}\leq-1+2\sigma\frac{g_{k-1}^Td_{k-1}}{\|g_{k-1}\|^2}\leq\frac{g_{k}^Td_{k}}{\|g_{k}\|^{2}}\leq -1. \end{eqnarray} $

综合(3.2)和(3.8)式可知充分下降性(3.1)式对$ k\geq1 $成立. 证毕.

基于$ \rm JLJW^{+} $方法的充分下降性(3.1)式, 下面给出$ \rm JLJW^{+} $算法的全局收敛性定理及其证明.

定理3.1  若假设$ \rm (H1) $和$ \rm (H2) $成立, 则由$ \rm JLJW^{+} $算法产生的点列$ \{x_k\} $满足

$ \liminf \limits_{k\to\infty}\|g_{k}\|=0. $

证  用反证法. 假设$ \liminf \limits_{k\to\infty}\|g_{k}\|\neq0, $则存在一个常数$ \gamma>0 $, 使得

$ \|g_{k}\|\geq \gamma, \ \forall\ k\geq1. $

一方面, 由(1.2)式, (3.1)式和假设(H2)可得

$ (1-\sigma)\|g_k\|^2\leq-(1-\sigma)g_{k}^Td_k\leq d_{k}^T(g_{k+1}-g_k)\leq \alpha_k L\|d_k\|^2. $

进而$ \alpha_k\geq\frac{(1-\sigma)\|g_k\|^2}{ L\|d_k\|^2} $. 又由(1.2)和(3.1)式有

(3.9) $ \begin{eqnarray} f(x_k)-f(x_{k+1})\geq-\delta\alpha_kg_{k}^Td_k\geq \delta\alpha_k\|g_k\|^2\geq \frac{\delta(1-\sigma)\|g_k\|^4}{ L\|d_k\|^2}. \end{eqnarray} $

另一方面, 由$ \rm JLJW^{+} $算法可知

(i) 当搜索方向$ d_k $为重启方向, 即$ d_k=-\tilde{\theta}_kg_{k}+\eta\frac{g_{k}^Td_{k-1}}{\|d_{k-1}\|^{2}}d_{k-1} $时, 将$ d_k $两边同时平方有

(3.10) $ \begin{eqnarray} \|d_k\|^{2}&=&\tilde{\theta}_k^2\|g_{k}\|^{2}-2\tilde{\theta_{k}}\eta\frac{(g_{k}^Td_{k-1})^{2}}{\|d_{k-1}\|^{2}}+ \eta^{2}\frac{(g_{k}^Td_{k-1})^{2}}{\|d_{k-1}\|^{4}}\|d_{k-1}\|^{2} \\ &=&(1+\eta\cos^2\vartheta_k)^2\|g_{k}\|^{2}-2(1+\eta\cos^2\vartheta_k)\eta\cos^2\vartheta_k\|g_{k}\|^{2} +\eta^2\cos^2\vartheta_k\|g_{k}\|^{2} \\ &\leq&[(2+2\eta^2\cos^4\vartheta_k)-2(1+\eta\cos^2\vartheta_k)\eta\cos^2\vartheta_k +\eta^2\cos^2\vartheta_k]\|g_{k}\|^{2}\\ &=&[2+(\eta^2-2\eta)\cos^2\vartheta_k]\|g_{k}\|^{2}\\ &\leq&2\|g_{k}\|^{2}, \end{eqnarray} $

其中$ \vartheta_k $为$ g_k $和$ d_{k-1} $的夹角.

(ii) 当搜索方向$ d_k=-\theta_kg_k+\beta_k^{\rm JLJW}d_{k-1} $时, 由(1.2), (3.1)和(3.6)式可知

(3.11) $ \begin{eqnarray} 0<\theta_k=1+\beta_k^{\rm JLJW}\frac{|g_k^Td_{k-1}|}{\|g_k\|^2}\leq1+\sigma\frac{|g_{k-1}^{\rm T}d_{k-1}|}{\|g_{k-1}\|^2}\leq\frac{1-\sigma}{1-2\sigma}. \end{eqnarray} $

将$ d_k $两边平方有

(3.12) $ \begin{eqnarray} \|d_k\|^{2}=\theta_k^2\|g_{k}\|^{2}-2\theta_k\beta_k^{\rm JLJW}g_k^Td_{k-1}+(\beta_k^{\rm JLJW})^{2}\|d_{k-1}\|^{2}. \end{eqnarray} $

根据(3.10)式和(3.12)式可知$ \rm JLJW^{+} $算法的搜索方向$ d_k $总是满足

(3.13) $ \begin{eqnarray} \|d_k\|^{2}\leq\nu\|g_{k}\|^{2}+2\theta_k|\beta_k^{\rm JLJW}g_k^Td_{k-1}|+(\beta_k^{\rm JLJW})^{2}\|d_{k-1}\|^{2}, \end{eqnarray} $

其中$ \nu=\max\{2, (\frac{1-\sigma}{1-2\sigma})^2\} $.

将(3.13)式两边同时除以$ \|g_{k}\|^{4} $, 再结合(1.2), (3.1), (3.6) 和(3.11)式可得

(3.14) $ \begin{eqnarray} \frac{\|d_k\|^{2}}{\|g_{k}\|^{4}}&\leq &\nu\frac{1}{\|g_{k}\|^{2}}+2\theta_k\beta_k^{\rm JLJW}\frac{|g_k^Td_{k-1}|}{\|g_{k}\|^{4}}+(\beta_k^{\rm JLJW})^{2}\frac{\|d_{k-1}\|^{2}}{\|g_{k}\|^{4}} \\ &\leq&\nu\frac{1}{\|g_{k}\|^{2}}+\frac{2(1-\sigma)}{1-2\sigma}\frac{1}{\|g_{k}\|^{2}}\frac{|g_k^Td_{k-1}|}{\|g_{k-1}\|^{2}} +\frac{\|d_{k-1}\|^{2}}{\|g_{k-1}\|^{4}} \\ &\leq&\nu\frac{1}{\|g_{k}\|^{2}}+\frac{2\sigma(1-\sigma)}{1-2\sigma}\frac{1}{\|g_{k}\|^{2}}\frac{|g_{k-1}^Td_{k-1}|}{\|g_{k-1}\|^{2}} +\frac{\|d_{k-1}\|^{2}}{\|g_{k-1}\|^{4}} \\ &\leq&\nu\frac{1}{\|g_{k}\|^{2}}+\frac{2\sigma(1-\sigma)}{(1-2\sigma)^2}\frac{1}{\|g_{k}\|^{2}} +\frac{\|d_{k-1}\|^{2}}{\|g_{k-1}\|^{4}} \\ &=&\omega\frac{1}{\|g_{k}\|^{2}}+\frac{\|d_{k-1}\|^{2}}{\|g_{k-1}\|^{4}}, \end{eqnarray} $

其中$ \omega=\nu+\frac{2\sigma(1-\sigma)}{(1-2\sigma)^2} $. 又因$ \frac{\|d_1\|^{2}}{\|g_1\|^{4}}=\frac{1}{\|g_{1}\|^{2}} $, 由递推公式(3.14)以及$ \|g_{k}\|\geq \gamma, $可得

(3.15) $ \begin{eqnarray} \frac{\|d_k\|^2}{\|g_k\|^4}\leq\sum\limits_{i=1}^{k}\limits\frac{\omega}{\|g_i\|^{2}}\leq\frac{k\omega}{\gamma^2}. \end{eqnarray} $

结合(3.9)和(3.15)式得

(3.16) $ \begin{eqnarray} \frac{\gamma^2}{k\omega}\leq\frac{\|g_k\|^4}{\|d_k\|^2}\leq\frac{L}{\delta(1-\sigma)}\left(f(x_k)-f(x_{k+1})\right). \end{eqnarray} $

另外, 由于$ \{x_k\}\subseteq\Lambda $, 故由假设(H1), (1.2)式以及(3.1)式可知: 数列$ \{f(x_k)\} $单调下降且有下界. 因此, $ \{f(x_k)\} $为收敛数列. 此结合(3.16)式可得

$ \frac{\gamma^2}{\omega}\sum\limits_{k=1}^{\infty}\limits\frac{1}{k}\leq\frac{L}{\delta(1-\sigma)}\lim\limits_{k\to\infty} \left(f(x_1)-f(x_{k+1})\right)<\infty. $

这与调和级数$ \sum_{k=1}^{\infty}\limits\frac{1}{k} $发散矛盾. 证毕.

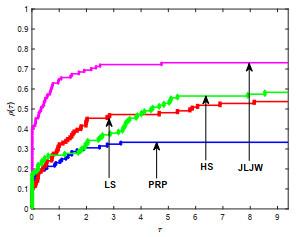
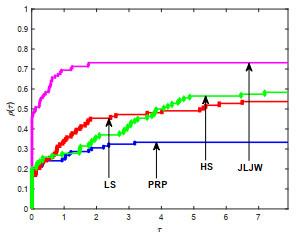
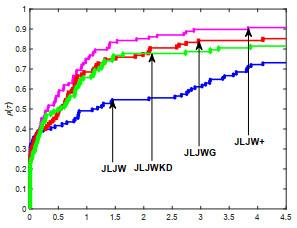
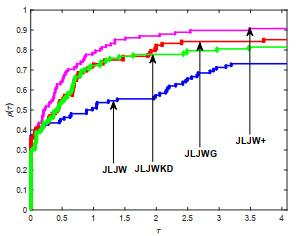
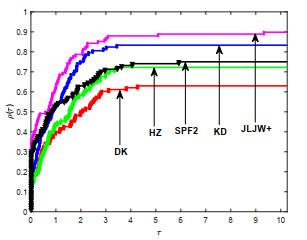
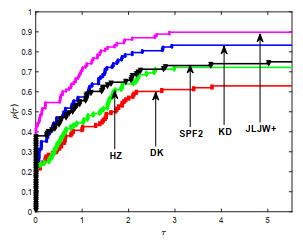
本节, 通过三组数值实验测试新方法的有效性. 第一组, 为测试改进的PRP型方法的有效性, 将JLJW方法与HS方法^[1], PRP方法^{[3, 4]}和LS方法^[6]进行对比; 第二组, 为测试新型重启方向的有效性, 将$ \rm JLJW^{+} $方法与JLJWG方法, JLJWKD方法, JLJW方法进行对比, 其中JLJWG方法表示将$ \rm JLJW^{+} $的重启方向替换为负梯度方向, JLJWKD方法表示将$ \rm JLJW^{+} $的重启方向替换为KD方法中的重启方向, 即(2.4)式; 第三组, 为测试$ \rm JLJW^{+} $方法的有效性, 将$ \rm JLJW^{+} $方法与现有数值表现较好的KD方法^[19], DK方法^[24], HZ方法^[25], SFP2方法^[14]进行比对. 三组测试都采用强Wolfe线搜索(1.2)计算步长, 都测试了108个相同的算例, 其中算例1-60取自CUTEr算例库^[26], 其余算例取自问题集^{[27, 28]}. 测试环境为Matlab R2016a, Windows10操作系统, 联想台式电脑(Intel(R)Core(TM)i7-7700CPU@3.60GHz)8GB内存. 相关参数选取如下: $ \delta=0.01 $, $ \sigma=0.1 $, $ r=0.8 $, $ \eta=0.05 $. 实验中, 选取的试探步长$ \alpha_{k, 0} $与前一步长$ \alpha_{k-1} $有关, 这样有助于提高Wolfe线搜索的效率. 具体的选取策略为

$ \begin{eqnarray} \alpha_{k, 0}=\left\{\begin{array}{ll}1, &k=1, \\ { }\alpha_{k-1}\frac{g_{k-1}^Td_{k-1}}{g_k^Td_k}, &k>1, \end{array}\right. \end{eqnarray} $

其中$ \alpha_{k, 0} $表示线搜索计算步长$ \alpha_{k} $的试探步长.

本文算法的终止准则为以下两种情形之一

(1) $ \| g_k\|\leq 10^{-6} $;

(2) 迭代次数$ {\rm Itr}>2000 $.

另外, 终止准则(2) 出现时认为该方法对相应例子失效, 并记为"F".

在试验中, 我们分别对迭代次数(Itr), CPU计算时间(Tcpu)及算法终止时梯度值$ \|g_*\| $ (精度)三个指标进行观察和比较, 同时, 我们还采用Dolan和Morè^[29]性能图对算法的CPU计算时间和迭代次数进行直观刻划. 由于三组测试均基于相同的测试问题及维数, 因此, 为了节省篇幅, 第一、第二组实验仅报告其数值结果性能图, 第三组报告其详细数值结果及性能图. 其中图 1–2对应第一组的测试结果, 图 3–4对应第二组的测试结果, 表 1–2及图 5–6对应第三组的测试结果. 从图 1–2可以看出JLJW方法的数值表现优于其他3个经典方法. 图 3–4说明本文构造的重启方向比负梯度方向以及Kou和Dai提出的重启方向(2.4) 更适合用来改进JLJW方法; 同时, 也说明本文提出的改进策略极大提高了JLJW方法的计算性能. 从表 1–2和图 5–6可以看出$ \rm JLJW^{+} $算法能够解决约90$ \% $的算例, 明显优于现有数值效果好的几个共轭梯度法.