1 引言
考虑如下形式的非线性方程组问题
其中
共轭梯度法、谱梯度法和谱共轭梯度法等一阶最优化方法在求解最优化问题方面受到了研究者的广泛关注, 这类方法迭代结构简单, 存储量小, 具有良好的局部和全局收敛性, 适合求解大规模问题. 近年来, 广大研究者热衷于利用一阶最优化方法的结构, 借助投影算子和无导数线搜索条件求解大规模非光滑的非线性方程组问题, 这类算法避免了计算和存储Jacobian矩阵. 如Cheng[6]在著名PRP共轭梯度法和超平面投影技术的基础上建立了求解无约束单调方程组问题的PRP型投影算法. Yu等[7]将改进的谱梯度法与投影法相结合建立了求解凸约束单调方程组的谱梯度投影算法. 受Livieris等[9]利用无记忆BFGS混合共轭梯度方法求解无约束优化问题的启发, Koorapetse和Kaelo[8]基于著名的HS和DY两种共轭梯度法, 借助投影算子, 建立了一种求解凸约束单调方程组问题的混合共轭梯度型投影算法. Liu等人[10]建立了一种求解凸约束单调方程组问题的修正无导数投影算法, 并在自适应无导数线搜索条件下证明了算法的全局收敛性. 基于PRP共轭梯度法与投影法, 刘金魁、孙悦和赵永祥[11]研究了一种求解凸约束伪单调方程组问题的无导数投影算法, 该算法在不需要假设方程组满足Lipschitz条件下具有全局收敛性和R-线收敛速度.
受上述文献的启发, 基于著名LS共轭梯度法和谱梯度法的结构, 借助投影算子, 本文进一步研究求解凸约束非线性伪单调方程组问题的谱LS型无导数投影算法, 其在不需要线搜索条件下能够保证搜索方向在每次迭代中满足充分下降性. 在常规假设和经典无导数线搜索条件下, 算法具有全局收敛性. 通过大量的数值实验和分析, 新算法对于给定的大规模问题是有效的和稳定的.
2 投影算法
为了建立约束问题的迭代算法, 本文需要借助投影算子, 即
其中
基于LS共轭梯度法与谱梯度法, 本文建立新的搜索方向, 即
其中
为了克服LS算法下降性弱的缺点, 我们选取适当的
其中
当
取
下面根据投影算子及新的搜索方向, 借助经典的无导数型线搜索技术, 本文建立求解凸约束伪单调方程组问题的谱LS型无导数投影算法, 其在每一步迭代均满足充分下降性质.
算法2.1 (SLSDF)
步骤0: 选取初始点
步骤1: 若
步骤2: 利用(2.3)计算搜索方向
步骤3: 计算
步骤4: 若
其中
步骤5: 设
下面定理在证明迭代算法的收敛性方面具有重要作用, 其证明参考谱参数的构造.
定理2.1 设序列
3 算法的收敛性
为了证明SLSDF算法对伪单调方程组问题的全局收敛性, 本文需要下面的假设条件.
假设3.1 (ⅰ) 问题(1.1)的解集
(ⅱ)
(ⅲ)
引理3.1 设
证 设
根据(2.5)和(3.3)式可得
利用上述不等式、(2.2)式和参数
由于
故序列
根据假设3.1(ⅲ)及序列
于是, 根据(3.4)式可得
进一步利用收敛级数的性质可知
这意味着结论(3.1)成立. 根据(2.2)式及参数
于是, 利用(3.1)式及上述不等式, 可得(3.2)式成立. 证毕.
注3.1 根据序列
引理3.2 设
证 根据(2.5)式可知,
于是, 根据(2.7)、(3.7)式及假设3.1(ⅲ), 可得
整理可得
结论(3.6)得证.证毕.
下面利用定理2.1和引理3.1–3.2证明SLSDF算法对凸约束伪单调方程组问题具有全局收敛性.
定理3.1 设
证 反证法证明. 假设(3.9)式不成立, 则存在一个正数
根据引理3.1可知, 序列
根据(2.7)和(3.10)式可得
根据(2.3)、(2.7)、(3.5)和(3.11)式可知
于是,利用(3.6)和(3.12)式有
又利用(3.1)式和
这显然产生矛盾. 因此, 假设命题(3.10)不成立, 结论(3.9)成立.
4 数值试验
算法终止条件为
问题1. 该问题来自文献[12], 并增加约束条件
问题2. 该问题来自文献[13], 其约束条件为
问题3. Tridiagonal exponential问题[14], 并增加约束条件
其中
问题4. ENGVAL函数[15]的梯度, 并增加约束条件
问题5. Discrete boundry value问题[16], 并增加约束条件
其中
问题6. 该问题来自文献[17], 并增加了约束条件
问题7. 该问题来自文献[17], 并增加了约束条件
为了检测SLSDF算法对大规模问题的有效性和适应性, 本文取测试问题的维数为
表 1 算法对问题1的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 10/0.27/8.35775E-06 | 9/0.05/7.69126E-06 | 10/0.13/6.24219E-06 | |
| 100000 | 11/0.54/5.36400E-06 | 10/0.35/4.40940E-06 | 13/0.44/3.06195E-06 | |
| 10000 | 11/0.07/3.95144E-06 | 10/0.05/2.24586E-06 | 11/0.42/2.52040E-06 | |
| 100000 | 12/0.59/2.53604E-06 | 10/0.35/7.10203E-06 | 11/0.36/1.95314E-06 | |
| 10000 | 14/0.15/5.38909E-06 | 18/0.27/8.08404E-06 | 13/0.09/2.45327E-06 | |
| 100000 | 15/0.63/3.45872E-06 | 19/0.84/8.64032E-06 | 13/0.48/7.75972E-06 | |
| 10000 | 10/0.07/3.16713E-06 | 16/0.16/8.47098E-06 | 10/0.08/5.68024E-06 | |
| 100000 | 11/0.62/1.47420E-06 | 17/0.74/9.05390E-06 | 11/0.35/7.97022E-06 | |
| 10000 | 11/0.06/4.81393E-06 | 11/0.05/5.31729E-06 | 12/0.07/4.65517E-06 | |
| 100000 | 12/0.52/3.08958E-06 | 12/0.45/3.04840E-06 | 11/0.32/4.10582E-06 | |
| 1000 | 18/0.46/5.95037E-06 | 23/0.02/7.65046E-06 | 18/0.02/7.26018E-06 | |
| 1000 | 14/0.01/2.53885E-06 | 17/0.02/2.36570E-06 | 17/0.01/3.03249E-06 | |
| 1000 | 18/0.01/2.69658E-06 | 16/0.01/9.89883E-06 | 19/0.01/4.60776E-06 | |
| 10000 | 16/0.25/3.56274E-06 | 19/0.1/8.93693E-06 | 20/0.07/2.70993E-06 | |
| 10000 | 17/0.09/8.58381E-06 | 16/0.06/8.76281E-06 | 24/0.08/3.85628E-06 | |
| 10000 | 16/0.08/2.41299E-06 | 21/0.08/3.38577E-06 | 20/0.06/4.22776E-06 |
表 2 算法对问题2的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 14/0.11/2.28152E-06 | 22/0.13/6.86367E-06 | 49/0.24/6.82665E-06 | |
| 100000 | 16/1.03/2.10679E-06 | 25/1.44/6.43402E-06 | 54/2.08/6.77842E-06 | |
| 10000 | 12/0.08/2.04626E-06 | 21/0.14/9.39860E-06 | 52/0.24/7.26662E-06 | |
| 100000 | 19/1.16/1.76761E-06 | 24/1.23/5.72030E-06 | 51/1.87/7.03466E-06 | |
| 10000 | 12/0.09/8.92636E-06 | 27/0.17/7.87962E-06 | 49/0.25/6.42977E-06 | |
| 100000 | 15/0.92/4.24272E-06 | 24/1.43/7.22225E-06 | 53/2.02/6.98044E-06 | |
| 10000 | 14/0.12/8.31650E-06 | 22/0.15/8.32467E-06 | 49/0.2/6.63369E-06 | |
| 100000 | 23/1.57/3.13326E-06 | 29/1.64/9.69912E-06 | 59/2.12/8.06344E-06 | |
| 10000 | 20/0.17/9.18226E-06 | 22/0.13/7.27369E-06 | 51/0.27/9.47091E-06 | |
| 100000 | 18/1.75/5.89499E-06 | 23/1.16/5.15380E-06 | 54/1.98/7.31554E-06 | |
| 1000 | 13/0.02/9.55053E-06 | 25/0.03/9.45970E-06 | 68/0.04/7.64093E-06 | |
| 1000 | 13/0.01/6.91733E-06 | 26/0.02/6.77331E-06 | 58/0.03/7.69436E-06 | |
| 1000 | 14/0.01/3.27047E-06 | 22/0.01/9.13867E-06 | 58/0.02/7.50824E-06 | |
| 10000 | 16/0.1/4.89654E-06 | 42/0.28/5.62731E-06 | 64/0.28/9.72200E-06 | |
| 10000 | 19/0.13/5.67477E-06 | 40/0.22/8.89704E-06 | 64/0.26/9.52940E-06 | |
| 10000 | 18/0.12/4.61617E-06 | 27/0.16/7.33332E-06 | 63/0.31/9.64623E-06 |
表 3 算法对问题3的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 17/0.07/2.81228E-06 | 16/0.06/8.52110E-06 | 57/0.24/9.14599E-06 | |
| 100000 | 16/0.39/8.13031E-06 | 20/0.49/6.11814E-06 | 44/0.81/8.87728E-06 | |
| 10000 | 15/0.06/9.95448E-06 | 16/0.06/3.98212E-06 | 58/0.14/9.11972E-06 | |
| 100000 | 15/0.39/4.47081E-06 | 18/0.42/4.45220E-06 | 45/0.81/8.73945E-06 | |
| 10000 | 14/0.06/5.53121E-06 | 12/0.05/1.99091E-06 | 23/0.08/8.77438E-06 | |
| 100000 | 15/0.36/5.62202E-06 | 15/0.37/9.14178E-06 | 40/0.73/7.49943E-06 | |
| 10000 | 16/0.12/4.56086E-06 | 13/0.05/1.27684E-06 | 53/0.16/9.12098E-06 | |
| 100000 | 18/0.41/9.53202E-06 | 18/0.42/2.94888E-06 | 40/0.73/9.09379E-06 | |
| 10000 | 14/0.05/6.46989E-06 | 17/0.06/3.78712E-06 | 56/0.14/9.14812E-06 | |
| 100000 | 17/0.41/8.76135E-06 | 15/0.34/7.77275E-06 | 41/0.72/8.76429E-06 | |
| 1000 | 15/0.02/5.12728E-06 | 14/0.02/6.96159E-06 | 70/0.03/6.06227E-06 | |
| 1000 | 16/0.01/3.31604E-06 | 15/0.01/5.33449E-06 | 71/0.02/6.04804E-06 | |
| 1000 | 15/0.01/8.42411E-06 | 17/0.01/3.22741E-06 | 67/0.02/9.92832E-06 | |
| 10000 | 17/0.06/3.04681E-06 | 17/0.07/1.89898E-06 | 57/0.15/9.11084E-06 | |
| 10000 | 17/0.06/3.77356E-06 | 17/0.05/3.52052E-06 | 57/0.12/9.21500E-06 | |
| 10000 | 17/0.05/3.04315E-06 | 16/0.04/6.01119E-06 | 53/0.12/9.08530E-06 |
表 4 算法对问题4的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 34/0.15/6.71745E-06 | 22/0.08/9.64604E-06 | 58/0.17/8.00695E-06 | |
| 100000 | 40/1.33/5.98689E-06 | 30/0.88/4.99211E-06 | 56/1.22/6.92717E-06 | |
| 10000 | 33/0.12/6.46636E-06 | 26/0.11/9.37117E-06 | 61/0.17/7.19919E-06 | |
| 100000 | 33/1.04/8.47901E-06 | 31/0.96/4.23145E-06 | 58/1.3/9.11678E-06 | |
| 10000 | 37/0.15/5.39551E-06 | 31/0.12/6.05411E-06 | 65/0.19/8.18695E-06 | |
| 100000 | 40/1.32/7.67252E-06 | 33/1.01/6.90460E-06 | 62/1.39/7.08876E-06 | |
| 10000 | 30/0.13/4.75619E-06 | 30/0.11/6.52395E-06 | 70/0.17/7.42661E-06 | |
| 100000 | 40/1.31/6.29701E-06 | 37/1.17/4.36692E-06 | 68/1.48/7.09583E-06 | |
| 10000 | 30/0.12/8.35595E-06 | 28/0.12/8.82222E-06 | 57/0.14/9.92298E-06 | |
| 100000 | 37/1.12/7.90263E-06 | 26/0.73/7.80168E-06 | 55/1.21/8.54528E-06 | |
| 1000 | 42/0.03/7.25125E-06 | 37/0.03/6.49794E-06 | 84/0.03/7.28839E-06 | |
| 1000 | 50/0.02/8.09325E-06 | 31/0.01/8.94628E-06 | 70/0.02/9.50344E-06 | |
| 1000 | 50/0.02/8.03816E-06 | 38/0.01/7.83207E-06 | 79/0.02/8.27614E-06 | |
| 10000 | 45/0.19/4.45461E-06 | 47/0.16/4.26260E-06 | 104/0.23/9.05904E-06 | |
| 10000 | 55/0.19/5.31741E-06 | 40/0.12/7.73662E-06 | 92/0.19/8.53725E-06 | |
| 10000 | 56/0.18/5.93166E-06 | 42/0.14/7.89234E-06 | 90/0.2/9.27884E-06 |
表 5 算法对问题5的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 15/0.2/9.30794E-06 | 24/0.26/8.99460E-06 | 53/0.41/7.45327E-06 | |
| 100000 | 25/2.93/6.43615E-06 | 19/1.78/8.38742E-06 | 55/4.19/9.53306E-06 | |
| 10000 | 17/0.25/8.73580E-06 | 26/0.29/9.71544E-06 | 57/0.46/8.26386E-06 | |
| 100000 | 34/3.94/6.56639E-06 | 21/2.03/8.86982E-06 | 60/4.54/6.42017E-06 | |
| 10000 | 37/0.45/6.52915E-06 | 31/0.35/6.52281E-06 | 199/1.46/9.56048E-06 | |
| 100000 | 54/6.35/7.12462E-06 | 26/2.58/9.96656E-06 | 200/13.6/8.85841E-06 | |
| 10000 | 33/0.41/3.86804E-06 | 29/0.34/4.86781E-06 | 63/0.5/8.09248E-06 | |
| 100000 | 49/5.59/6.35406E-06 | 29/2.91/9.44800E-06 | 62/4.71/7.91238E-06 | |
| 10000 | 19/0.25/7.35353E-06 | 27/0.3/7.77302E-06 | 59/0.5/8.37336E-06 | |
| 100000 | 32/3.82/6.28651E-06 | 23/2.34/5.85602E-06 | 55/4.19/6.79479E-06 | |
| 1000 | 23/0.04/9.62598E-06 | 31/0.05/8.91162E-06 | 201/0.15/8.25980E-06 | |
| 1000 | 25/0.03/5.50717E-06 | 34/0.04/9.17404E-06 | 197/0.14/7.45662E-06 | |
| 1000 | 24/0.03/3.32316E-06 | 34/0.04/7.69712E-06 | 64/0.05/9.94895E-06 | |
| 10000 | 33/0.4/3.16616E-06 | 34/0.47/8.97918E-06 | 67/0.49/7.79202E-06 | |
| 10000 | 37/0.43/8.07076E-06 | 33/0.33/8.94202E-06 | 67/0.49/7.33025E-06 | |
| 10000 | 28/0.38/5.46344E-06 | 38/0.42/5.74752E-06 | 69/0.49/7.27176E-06 |
表 6 算法对问题6的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 12/0.04/3.53915E-06 | 10/0.04/1.82363E-06 | 26/0.05/7.73313E-06 | |
| 100000 | 13/0.28/2.65924E-06 | 10/0.19/5.76683E-06 | 28/0.4/6.73508E-06 | |
| 10000 | 13/0.04/3.17492E-06 | 10/0.04/4.73744E-06 | 23/0.05/7.15729E-06 | |
| 100000 | 14/0.32/2.38556E-06 | 11/0.21/1.76149E-06 | 25/0.42/6.23357E-06 | |
| 10000 | 9/0.03/1.67451E-06 | 11/0.04/1.43408E-06 | 23/0.05/6.28294E-06 | |
| 100000 | 9/0.18/5.29525E-06 | 11/0.19/4.53495E-06 | 25/0.39/5.47206E-06 | |
| 10000 | 11/0.03/6.75249E-06 | 11/0.03/1.44773E-06 | 25/0.05/6.65329E-06 | |
| 100000 | 12/0.24/5.07367E-06 | 11/0.21/4.57811E-06 | 27/0.41/5.79461E-06 | |
| 10000 | 12/0.04/7.54576E-06 | 11/0.03/1.80320E-06 | 26/0.05/9.15601E-06 | |
| 100000 | 13/0.27/5.66971E-06 | 11/0.19/5.70223E-06 | 28/0.42/7.97432E-06 | |
| 1000 | 15/0.01/4.65847E-06 | 21/0.02/8.13107E-06 | 30/0.02/8.92921E-06 | |
| 1000 | 62/0.01/5.37181E-06 | 124/0.04/9.46999E-06 | 376/0.05/9.07041E-06 | |
| 1000 | 36/0.01/6.96704E-06 | 114/0.03/8.90380E-06 | 283/0.04/9.54975E-06 | |
| 10000 | 67/0.13/8.04304E-06 | 38/0.07/8.47795E-06 | 254/0.33/7.17963E-06 | |
| 10000 | 29/0.06/7.79403E-06 | 28/0.05/9.51788E-06 | 142/0.18/7.03547E-06 | |
| 10000 | 30/0.05/7.67295E-06 | 32/0.06/8.66574E-06 | 371/0.43/7.84702E-06 |
表 7 算法对问题7的测试结果
| Intp | Dim | SLSDF | HSDF | LJJCGPM |
| NI/time/ | NI/time/ | NI/time/ | ||
| 10000 | 6/0.03/3.45393E-07 | 17/0.06/5.54564E-06 | 18/0.05/5.65483E-06 | |
| 100000 | 6/0.2/1.09223E-06 | 18/0.44/6.05833E-06 | 19/0.38/6.55944E-06 | |
| 10000 | 6/0.03/6.20504E-07 | 16/0.05/4.33525E-06 | 18/0.05/8.39471E-06 | |
| 100000 | 6/0.2/1.96221E-06 | 17/0.52/4.73604E-06 | 19/0.4/9.73760E-06 | |
| 10000 | 7/0.03/4.59950E-07 | 17/0.06/8.08326E-06 | 17/0.05/5.97154E-06 | |
| 100000 | 7/0.24/1.45449E-06 | 18/0.44/8.83056E-06 | 18/0.35/6.92680E-06 | |
| 10000 | 5/0.02/4.07959E-06 | 17/0.06/6.42071E-06 | 18/0.05/6.74412E-06 | |
| 100000 | 6/0.18/2.53313E-07 | 18/0.43/7.01431E-06 | 19/0.39/7.82298E-06 | |
| 10000 | 5/0.03/3.42253E-07 | 14/0.05/9.48173E-06 | 15/0.05/8.28338E-06 | |
| 100000 | 5/0.16/1.08230E-06 | 16/0.42/3.57842E-06 | 16/0.33/9.60847E-06 | |
| 1000 | 14/0.01/8.67102E-07 | 17/0.02/5.33128E-06 | 17/0.02/8.07045E-06 | |
| 1000 | 13/0.01/9.50521E-06 | 17/0.01/5.32577E-06 | 17/0.01/8.23321E-06 | |
| 1000 | 15 0.01/7.80850E-06 | 17/0.01/5.27943E-06 | 17/0.01/7.88612E-06 | |
| 10000 | 14/0.05/6.96719E-06 | 18/0.05/5.81512E-06 | 18/0.05/9.32633E-06 | |
| 10000 | 14/0.04/5.16981E-06 | 18/0.06/5.81045E-06 | 18/0.04/9.52345E-06 | |
| 10000 | 14/0.04/6.15402E-06 | 18/0.04/5.82664E-06 | 18/0.03/9.36081E-06 |
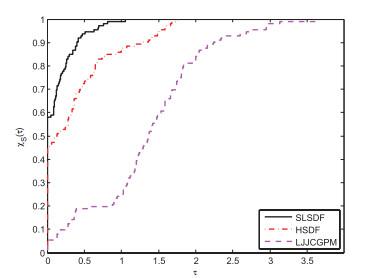
图 1
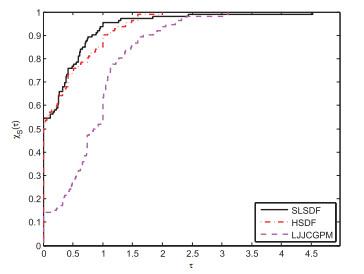
图 2
参考文献
Superline convergence of a Newton-type algorithm for monotone equations
A globally and superlinearly convergent Gauss-Newton based BFGS method for symmetric equations
A modified BFGS type quasi-Newton method with line search for symmetric nonlinear equations problems
DOI:10.1016/j.cam.2019.112454 [本文引用: 1]
A PRP type method for systems of monotone equations
DOI:10.1016/j.mcm.2009.04.007 [本文引用: 1]
Spectral gradient projection method for monotone nonlinear equations with convex constraints
DOI:10.1016/j.apnum.2009.04.004 [本文引用: 1]
A derivative-free conjugate gradient projection method based on the memoryless BFGS update
DOI:10.26637/MJM0802/0031 [本文引用: 1]
A descent hybrid conjugate gradient method based on the memoryless BFGS update
DOI:10.1007/s11075-018-0479-1 [本文引用: 1]
A new conjugate gradient projection method for convex constrained nonlinear equations
凸约束伪单调方程组的无导数投影算法
DOI:10.12286/jssx.j2020-0659 [本文引用: 2]
A derivative-free projection algorithm for solving pseudo-monotone equations with convex constraints
DOI:10.12286/jssx.j2020-0659 [本文引用: 2]
An efficient three-term conjugate gradient method for nonlinear monotone equations with convex constraints
DOI:10.1007/s10092-018-0244-9 [本文引用: 1]
An efficient projection-based algorithm without Lipschitz continuity for large-scale nonlinear pseudo-monotone equations
An efficient implementation of Merrill's method for sparse or partially separable systems of nonlinear equations
CUTEr: constrained and unconstrained testing enviroment
DOI:10.1145/200979.201043 [本文引用: 1]
Testing uncosntrained optimization software
DOI:10.1145/355934.355936 [本文引用: 1]
Modified matrix-free methods for solving system of nonlinear equations
Benchmarking optimization software with performance profiles
DOI:10.1007/s101070100263 [本文引用: 1]