1 引言
糖尿病治疗的目标是控制患者血糖浓度维持在正常范围内, 常用的治疗方式是服用降糖药和注射胰岛素, 其中连续地皮下胰岛素注射治疗可以通过安置胰岛素泵(开环方法) 来实现, 但是传统的治疗方式容易使患者发生低血糖或者因血糖控制不佳而导致各种并发症, 并危及患者的生命. 为了解决这个问题, 学者们开始考虑使用现代控制技术制造出能够代替胰腺的"人工胰腺", 通过预测血糖的变化来给患者供给适量的胰岛素, 最终达到控制血糖的目的. 为此, 学者们提出了不同的数学模型来模拟血糖-胰岛素相互间的作用, 希望为糖尿病提供更有效、更经济的疗法. 数学模型已成为了解葡萄糖-胰岛素调节系统的重要工具, 并给糖尿病患者提供更合理的胰岛素使用方法. 基于Bolie[3]的开创性工作, 许多著名的胰岛素-葡萄糖模型相继被研究[4-9]. 例如, Ackerman等[4-5]建立了一种口服葡萄糖耐量测试模型, 该模型可测量患者利用特定量葡萄糖的能力. Li等模拟了葡萄糖-胰岛素调节系统[8]并研究了具有两个时滞的胰岛素调节系统[9]. Topp等[10]通过考虑包含
其中
其中
在本文中, 除非另有说明,
本文安排如下: 在第2节, 得到系统正平衡点的存在性并证明其是全局渐进稳定的. 第3节研究随机系统的全局正解的存在唯一性、随机持久性和平稳分布的存在性. 第4节通过数值模拟来验证理论分析的结果. 在第5节, 我们进行简要的讨论并总结主要的结果.
2 确定性模型
确定性模型(1.1) 的正平衡点
由方程(2.1) 可得
令
易得,
其特征方程为
由Routh-Hurwitz判据可得, 系统(1.1) 的正平衡点
定理2.1 系统(1.1) 存在唯一的正平衡点, 且该平衡点是局部渐进稳定的.
下面我们将证明其全局稳定性.
定义
计算可得
由Dulac判别法可知, 系统(1.1) 无闭轨线, 因此正平衡点
定理2.2 系统(1.1) 存在唯一的正平衡点, 且该平衡点是全局渐进稳定的.
3 随机模型
本节我们将研究随机模型(1.2) 的动力学. 首先我们证明对于任意的正初始值, 系统(1.2) 存在唯一的全局正解.
3.1 全局正解
定理3.1 对于任意给定的初始条件
证 显然, 系统(1.2) 系数满足局部Lipschitz条件, 因此对任意的
令
定义
假设
定义如下
由It
其中
其中
对式(3.2) 两边同时从
其中
对式(3.3) 两边同时取期望可得
令
由式(3.4) 可知
其中
注3.1 定理3.1表明, 对于任意的正初始值, 系统(1.2) 依概率1存在唯一正解. 由系统(1.2) 可知
我们考虑如下方程
由文献[24]可知
通过随机微分方程比较定理可得
注3.2 通常而言, 相较于唯一的全局正解, 系统的持久性更有实际意义, 因为它预示着糖尿病病症动力学的长期水平. 因此, 我们将在下一部分探讨随机模型(1.2) 的持久性.
3.2 随机持久
本节将讨论随机系统(1.2) 的持久性. 首先, 我们给出随机持久的定义.
定义3.1[25] 对于任意给定的初始条件
则称随机系统(1.2) 为随机持久的.
定理3.2 随机系统(1.2) 是随机持久的.
证 设
首先我们证明
其中
对两边从
两边同时取期望可得
即
对任意
于是有
即
令
显然, 存在常数
对两边从
即
对任意
即
因此
于是,
下面, 我们证明
其中
与不等式(3.8) 证明类似, 对任意
最后我们证明, 对任意
定义
同样地, 对任意
综上所述, 由式(3.7)–(3.10) 可得随机系统(1.2) 是随机持久的.
3.3 平稳分布
为了证明系统(1.2) 存在唯一的遍历平稳分布, 我们先给出一些已有的结论.
设
其扩散矩阵为
引理3.1[26] 对Markov过程
则Markov过程
定理3.3 对任意初始值
证 为了证明定理3.3, 我们需要验证引理3.1中的条件
显然满足条件
由It
其中
考虑如下开集
将
于是有
情形1 在区域
情形2 在区域
综上所述, 对任意的
4 数值模拟
为了验证上述理论结果, 我们将给出对确定性模型(1.1) 以及随机模型(1.2) 数值模拟的结果. 对于随机系统(1.2), 我们采用Milstein高阶方法[27], 其对应的离散方程为
其中
对于确定性系统(1.1) 和随机系统(1.2), 取初始值
表 1 数值模拟参数取值
首先, 由定理2.1和定理2.2可知, 系统存在唯一的正平衡点, 且该平衡点是全局渐进稳定的(如图 1). 下面, 改变
图 1
图 1
系统(1.1) 的正平衡点
其余参数取值见
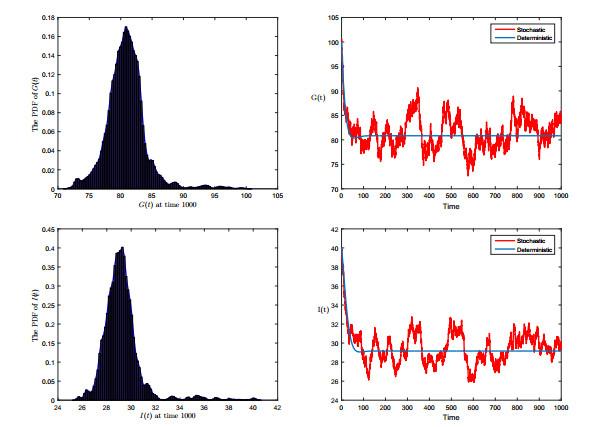
图 2
图 2
左侧为随机模型(1.2) 的密度函数图; 右侧为随机模型(1.2) 及其对应的确定性的解, 其初始条件为
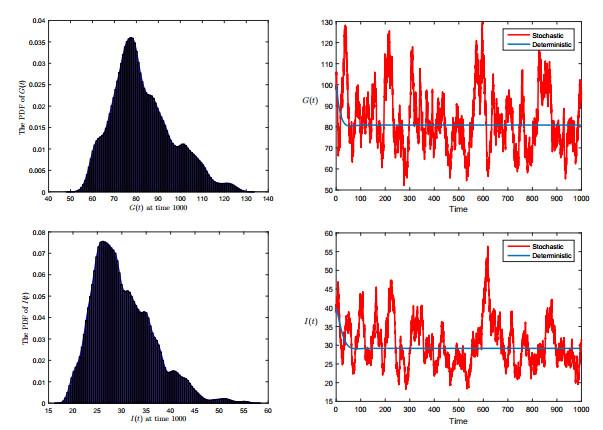
图 3
图 3
左侧为随机模型(1.2) 的密度函数图; 右侧为随机模型(1.2) 及其对应的确定性的解, 其初始条件为
5 结论
本文建立并研究了确定性葡萄糖-胰岛素模型及其相应的随机模型的动力学性质. 我们通过理论分析得到模型(1.1) 存在唯一全局渐进稳定的正平衡点
参考文献
National institute of diabetes and digestive and kidney diseases
National institute of diabetes and digestive and kidney diseases
Pathophysiology of type 2 in youth: the evolving chameleon
DOI:10.1590/S0004-27302009000200008 [本文引用: 1]
Coefficients of normal blood glucose regulation
DOI:10.1152/jappl.1961.16.5.783 [本文引用: 1]
A mathematical model of the glucose-tolerance test
DOI:10.1088/0031-9155/9/2/307 [本文引用: 2]
Model studies of blood-glucose regulation
DOI:10.1007/BF02476465 [本文引用: 1]
Hormonal effects on glucose regulation
Mathematical modeling and qualitative analysis of insulin therapies
DOI:10.1016/j.mbs.2007.05.008 [本文引用: 2]
Analysis of a model of the glucose-insulin regulatory system with two delays
DOI:10.1137/050634001 [本文引用: 11]
A Model of β-cell mass, insulin, and glucose kinetics: pathways to diabetes
DOI:10.1006/jtbi.2000.2150 [本文引用: 1]
Dynamics of glucose and insulin concentration connected to the β-cell cycle: model development and analysis
DOI:10.1186/1742-4682-9-46 [本文引用: 1]
The subcutaneous route to insulin-dependent diabetes therapy
DOI:10.1109/51.897828 [本文引用: 1]
A critical review of mathematical models and data used in diabetology
Modeling approaches to type 2 diabetes
DOI:10.1089/152091504322783396
Pharmacokinetic/pharmacodynamic modelling in diabetes mellitus
DOI:10.2165/00003088-200847070-00001
Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview
The intravenous route to blood glucose control
Mathematical models of energy homeostasis
DOI:10.1098/rsif.2008.0216 [本文引用: 1]
Modeling the glucose-insulin regulatory system and ultradian insulin secretory oscillations with two explicit time delays
DOI:10.1016/j.jtbi.2006.04.002 [本文引用: 1]
Modeling impulsive injections of insulin: towards artificial pancreas
DOI:10.1137/110860306 [本文引用: 9]
Effects of noise exposure on systemic and tissue-level markers of glucose homeostasis and insulin resistance in male mice
The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms
DOI:10.1007/s11071-017-3971-6 [本文引用: 1]
Long-term analysis of a stochastic SIRS model with general incidence rates
DOI:10.1137/19M1246973 [本文引用: 1]
Permanence of stochastic lotka-volterra systems
DOI:10.1007/s00332-016-9337-2 [本文引用: 1]
An algorithmic introduction to numerical simulations of stochastic differentila equations
DOI:10.1137/S0036144500378302 [本文引用: 1]
Optimal harvesting of a stochastic mutualism model with regime-switching
Stationary distribution of a stochastic hybrid phytoplankton model with allelopathy
DOI:10.1186/s13662-020-03088-9
Stationary distribution of a stochastic ratio-dependent predator-prey system with regime-switching
Persistence and ergodicity of a stochastic single species model with Allee effect under regime switching
DOI:10.1016/j.cnsns.2017.11.028
The stationary distribution and ergodicity of a stochastic phytoplankton allelopathy model under regime switching
DOI:10.1016/j.cnsns.2016.01.013
Average break-even concentration in a simple chemostat model with telegraph noise
DOI:10.1016/j.nahs.2018.03.007
A stochastic SIRS epidemic model with non-monotone incidence rate under regime-switching
DOI:10.1016/j.jfranklin.2019.09.009
Coexistence in a two species chemostat model with Markov switchings
DOI:10.1016/j.aml.2019.03.005 [本文引用: 1]