一类随机葡萄糖-胰岛素模型动力学分析

摘要/Abstract

摘要：

该文研究了一类葡萄糖-胰岛素模型及其相应的随机模型的全局动力学.对于确定性模型，证明存在唯一的平衡点，且该平衡点是全局渐近稳定.对于随机模型，证明系统全局正解的存在唯一性以及系统解的随机持久性.利用Hasminskiis方法，证明系统存在唯一遍历的平稳分布.最后，通过数值模拟验证了理论结果并发现：（i）预测血糖浓度峰值大小的难度总是随着环境波动强度的增加而增加；（ii）环境波动会导致血糖浓度和胰岛素浓度的不规则振荡.此外，血糖浓度和胰岛素浓度的震荡幅度总是随着环境波动强度的增加而增加.

关键词: 2型糖尿病, 全局稳定性, 环境波动, 平稳分布和遍历性

Abstract:

In this paper, we investigate the global dynamics of a glucose-insulin model and its corresponding stochastic differential equation version. For the deterministic model, we show that there exists a unique equilibrium point, which is globally asymptotically stable for all parameter values. For the stochastic model, we show that the system admits unique positive global solution starting from the positive initial value and derive the stochastic permanence of the solutions of the stochastic system. In addition, by using Hasminskiis methods, we prove that there exists a unique stationary distribution and it has ergodicity. Finally, numerical simulations are carried out to support our theoretical results. It is found that: (ⅰ) the difficulty of the prediction of the peak size of the plasma glucose concentration always increases with the increase of the intensity of environmental fluctuations; (ⅱ) environmental fluctuations can result in the irregular oscillating of the plasma glucose concentration and plasma insulin concentration. Moreover, the volatility of the plasma glucose concentration and plasma insulin concentration always increase with the increase of the intensity of environmental fluctuations.

Key words: Type 2 diabetes mellitus, Global stability, Environmental fluctuations, Stationary distribution and ergodicity

中图分类号:

O211.6

李江,蓝桂杰,张树文,魏春金. 一类随机葡萄糖-胰岛素模型动力学分析[J]. 数学物理学报, 2021, 41(6): 1937-1949.

Jiang Li,Guijie Lan,Shuwen Zhang,Chunjin Wei. Dynamics Analysis of a Stochastic Glucose-Insulin Model[J]. Acta mathematica scientia,Series A, 2021, 41(6): 1937-1949.

图/表 4

表 1

图 1

图 2

图 3

参考文献 35

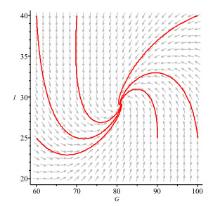
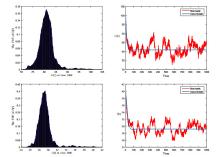
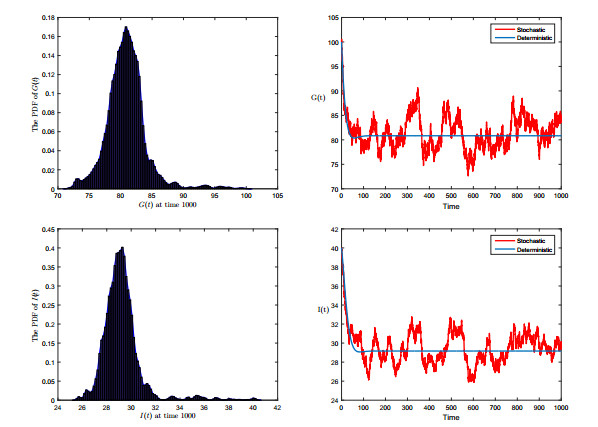
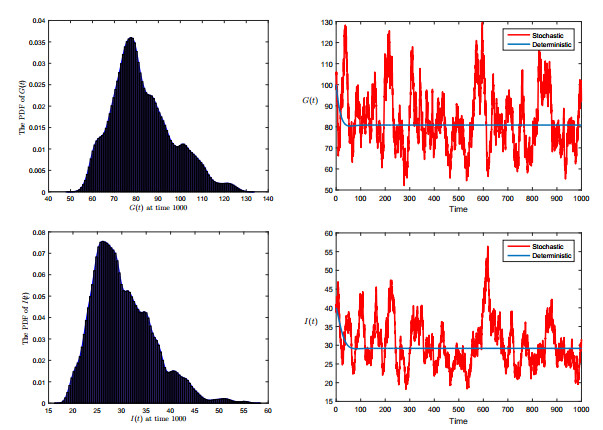
1	王林, 黄亚明. National institute of diabetes and digestive and kidney diseases. 中华内科杂志, 2010, (8): 695- 695
	Wang L , Huang Y M . National institute of diabetes and digestive and kidney diseases. Chinese Journal of Internal Medicine, 2010, (8): 695- 695
2	Tfayli H , Arslanian S . Pathophysiology of type 2 in youth: the evolving chameleon. Arq Bras Endocrinol, 2009, 53 (2): 165- 174 doi: 10.1590/S0004-27302009000200008
3	Bolie V W . Coefficients of normal blood glucose regulation. J Appl Physiol, 1961, 16 (5): 783- 790 doi: 10.1152/jappl.1961.16.5.783
4	Ackerman E , Rosevear J W , Mcguckin W F . A mathematical model of the glucose-tolerance test. Phys Med Biol, 1964, 9 (2): 203- 213 doi: 10.1088/0031-9155/9/2/307
5	Ackerman E , Gatewood L C , Rosevear J W , et al. Model studies of blood-glucose regulation. Bull Math Biophys, 1965, 27 (1): 21- 37 doi: 10.1007/BF02476465
6	Sulston K W , Ireland W P , Praught J C . Hormonal effects on glucose regulation. Atl Electron J Math, 2006, 1 (1): 31- 46
7	Divanovi H, Muli D, Padalo A, et al. Effects of electrical stimulation as a new method of treating diabetes on animal models: Review// Badnjevic A, et al. CMBEBIH. Singapore: Springer, 2017: 253-258
8	Wang H , Li J , Yang K . Mathematical modeling and qualitative analysis of insulin therapies. Math Biosci, 2007, 210 (1): 17- 33 doi: 10.1016/j.mbs.2007.05.008
9	Li J , Kuang Y . Analysis of a model of the glucose-insulin regulatory system with two delays. Siam J Appl Math, 2007, 67 (3): 757- 776 doi: 10.1137/050634001
10	Topp B , Promislow K , Devries G , et al. A Model of β-cell mass, insulin, and glucose kinetics: pathways to diabetes. J Theor Bio, 2000, 206 (4): 605- 619 doi: 10.1006/jtbi.2000.2150
11	Hernandez R D, Lyles D J, Rubin D B, et al. A model of β-cell mass, insulin, glucose and receptor dynamics with applications to diabetes[R]. Technical Report, Biometric Department, MTBI Cornell University, 2001
12	Gallenberger M , Castell WZ . Dynamics of glucose and insulin concentration connected to the β-cell cycle: model development and analysis. Theor Biol Med Model, 2012, 9 (1): 46- 46 doi: 10.1186/1742-4682-9-46
13	Bellazzi R , Nucci G , Cobelli C . The subcutaneous route to insulin-dependent diabetes therapy. IEEE Eng Med Biol, 2001, 20 (1): 54- 64 doi: 10.1109/51.897828
14	Boutayeb A , Chetouani A . A critical review of mathematical models and data used in diabetology. BioMed Eng OnLine, 2006, 5 (1): 43 doi: 10.1186/1475-925X-5-43
15	Kansal A R . Modeling approaches to type 2 diabetes. Diabetes Technol The, 2004, 6 (1): 39- 47 doi: 10.1089/152091504322783396
16	Landersdorfer C , Jusko W . Pharmacokinetic/pharmacodynamic modelling in diabetes mellitus. Clin Pharmacokinet, 2008, 47 (7): 417- 448 doi: 10.2165/00003088-200847070-00001
17	Makroglou A , Li J , Yang K . Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview. Appl Numer Math, 2006, 56 (3/4): 559- 573
18	Parker R S , Doyle F , Peppas N A . The intravenous route to blood glucose control. IEEE Eng Med Biol, 2001, 20 (1): 65- 73 doi: 10.1109/51.897829
19	Pattaranit R , Berg H . Mathematical models of energy homeostasis. J R Soc Interface, 2008, 5 (27): 1119- 1153 doi: 10.1098/rsif.2008.0216
20	Li J , Yang K , Mason C C . Modeling the glucose-insulin regulatory system and ultradian insulin secretory oscillations with two explicit time delays. J Theor Biol, 2006, 242 (3): 722- 735 doi: 10.1016/j.jtbi.2006.04.002
21	Huang M , Li J , Song X , et al. Modeling impulsive injections of insulin: towards artificial pancreas. SIAM J Appl Math, 2012, 72 (5): 1524- 1548 doi: 10.1137/110860306
22	Liu L , Wang F , Lu H , et al. Effects of noise exposure on systemic and tissue-level markers of glucose homeostasis and insulin resistance in male mice. Environ Health Perspect, 2016, 124, 1390- 1398 doi: 10.1289/EHP162
23	Yu X , Yuan S , Zhang T . The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms. Nonlinear Dyn, 2018, 91, 1653- 1668 doi: 10.1007/s11071-017-3971-6
24	Nguyen D , Yin G , Zhu C . Long-term analysis of a stochastic SIRS model with general incidence rates. Siam J Appl Math, 2020, 80 (2): 814- 838 doi: 10.1137/19M1246973
25	Liu M , Fan M . Permanence of stochastic lotka-volterra systems. J Nonl Sci, 2017, 27 (2): 425- 452 doi: 10.1007/s00332-016-9337-2
26	Khas'Miniskii R. Stochastic Stability of Differential Equations. Alphen aan den Rijn: Sijthoff and Noordhoff, 1980
27	Higham Desmond J . An algorithmic introduction to numerical simulations of stochastic differentila equations. Siam Rev, 2001, 43, 525- 546 doi: 10.1137/S0036144500378302
28	Liu M , Bai C . Optimal harvesting of a stochastic mutualism model with regime-switching. Appl Math Comput, 2020, 373, 125040
29	Ji W , Wang Z , Hu G . Stationary distribution of a stochastic hybrid phytoplankton model with allelopathy. Adv Differ Equ, 2020, 2020, 632 doi: 10.1186/s13662-020-03088-9
30	Wang Z , Deng M , Liu M . Stationary distribution of a stochastic ratio-dependent predator-prey system with regime-switching. Chaos Solitons Fract, 2020, 2020, 110462
31	Yu X , Yuan S , Zhang T . Persistence and ergodicity of a stochastic single species model with Allee effect under regime switching. Commun Nonlinear Sci, 2018, 59, 359- 374 doi: 10.1016/j.cnsns.2017.11.028
32	Zhao Y , Yuan S , Zhang T . The stationary distribution and ergodicity of a stochastic phytoplankton allelopathy model under regime switching. Commun Nonlinear Sci, 2016, 37, 131- 142 doi: 10.1016/j.cnsns.2016.01.013
33	Xu C , Yuan S , Zhang T . Average break-even concentration in a simple chemostat model with telegraph noise. Nonlinear Anal Hybr, 2018, 29, 373- 382 doi: 10.1016/j.nahs.2018.03.007
34	Lan G , Lin Z , Wei C , et al. A stochastic SIRS epidemic model with non-monotone incidence rate under regime-switching. J Franklin Inst, 2019, 356 (16): 9844- 9866 doi: 10.1016/j.jfranklin.2019.09.009
35	Zhao D , Liu H . Coexistence in a two species chemostat model with Markov switchings. Appl Math Lett, 2019, 94, 266- 271 doi: 10.1016/j.aml.2019.03.005

参数	数值	单位	参考
$G_{in}$	$2.16$	$mg/dl/\min$	[9, 21]
$S_k$	$2$	$\min^{-1}$	—
$S_g$	$5\times 10^{-6}$	$\min^{-1}$	[9, 21]
$S_i$	$0.1$	$\min^{-1}$	[9, 21]
$n$	$80$	$mg$	[9, 21]
$m$	$4$	—	—
$r$	$80$	$mg$	[9, 21]
$\sigma$	$6.27$	$mU/\min$	[9, 21]
$\alpha$	$105$	$mg$	[9, 21]
$d_i$	$0.08$	$\min^{-1}$	[9, 21]

[1]	丰利香,王德芬. 具有隔离和不完全治疗的传染病模型的全局稳定性[J]. 数学物理学报, 2021, 41(4): 1235-1248.
[2]	周永辉. 一类具有时滞的非局部反应扩散方程非单调临界行波解的全局稳定性[J]. 数学物理学报, 2020, 40(4): 983-992.
[3]	靖晓洁, 赵爱民, 刘桂荣. 考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性[J]. 数学物理学报, 2019, 39(4): 909-917.
[4]	韦爱举, 张新建, 王俊义, 李科赞. 一类埃博拉传染病模型的动力学分析[J]. 数学物理学报, 2017, 37(3): 577-592.
[5]	黄祖达. 一类具反馈控制的时滞飞蝇方程的伪概周期解[J]. 数学物理学报, 2016, 36(3): 558-568.
[6]	李玉环, 周军, 穆春来. 对带有非局部时滞和扩散的捕食者-食饵系统的稳定性分析[J]. 数学物理学报, 2012, 32(3): 475-488.
[7]	崔诚, 王晓, 高飞, 刘安平. 多元产品价格互惠时滞模型的周期解和概周期解及其全局稳定性[J]. 数学物理学报, 2011, 31(6): 1718-1729.
[8]	吴事良;李万同. 具有阶段结构的Lotka-Volterra合作系统的稳定性和行波解[J]. 数学物理学报, 2008, 28(3): 454-464.
[9]	桂占吉; 贾敬; 葛渭高. 具有时滞的单种群扩散模型的全局稳定性[J]. 数学物理学报, 2007, 27(3): 496-505.
[10]	梁志清;陈兰荪. 离散Leslie捕食与被捕食系统周期解的稳定性[J]. 数学物理学报, 2006, 26(4): 634-640.
[11]	曾志刚, 廖晓昕. 无界变时滞神经网络全局稳定性[J]. 数学物理学报, 2005, 25(5): 621-626.
[12]	原三领, 马知恩, 韩茂安. 一类含时滞SIS流行病模型的全局稳定性[J]. 数学物理学报, 2005, 25(3): 349-356.
[13]	宋新宇, 肖燕妮, 陈兰荪. 具有时滞的生态流行病模型的稳定性和Hopf分支[J]. 数学物理学报, 2005, 25(1): 57-66.
[14]	杨昌利, 阮荣耀, 龚妙昆. 一类不确定性非线性系统的状态反馈鲁棒自适应控制器的设计与分析[J]. 数学物理学报, 2004, 24(1): 26-37.
[15]	黄长水阮荣耀. 一类具有有界扰动的非线性系统的输出反馈自适应控制[J]. 数学物理学报, 2000, 20(3): 405-413.